Difference between revisions of "Hypostatic abstraction"
Jon Awbrey (talk | contribs) (JPEG → PNG) |
Jon Awbrey (talk | contribs) (+ syllabus) |
||
| Line 1: | Line 1: | ||
| − | '''Hypostatic abstraction''' is a formal operation that takes an element of information, as expressed in a proposition <math>X\ \operatorname{is}\ Y,</math> and conceives its information to consist in the relation between that subject and another subject, as expressed in the proposition <math>X\ \operatorname{has}\ Y\!\operatorname{-ness}.</math> The existence of the abstract subject <math>Y\!\operatorname{-ness}</math> consists solely in the truth of those propositions that contain the concrete predicate <math>Y.\!</math> Hypostatic abstraction is known under many names, for example, ''hypostasis'', ''objectification'', ''reification'', and ''subjectal abstraction''. The object of discussion or thought thus introduced is termed a ''[[hypostatic object]]''. | + | '''Hypostatic abstraction''' is a [[is::formal operation]] that takes an element of information, as expressed in a proposition <math>X\ \operatorname{is}\ Y,</math> and conceives its information to consist in the relation between that subject and another subject, as expressed in the proposition <math>X\ \operatorname{has}\ Y\!\operatorname{-ness}.</math> The existence of the abstract subject <math>Y\!\operatorname{-ness}</math> consists solely in the truth of those propositions that contain the concrete predicate <math>Y.\!</math> Hypostatic abstraction is known under many names, for example, ''[[aka::hypostasis]]'', ''[[aka::objectification]]'', ''[[aka::reification]]'', and ''[[aka::subjectal abstraction]]''. The object of discussion or thought thus introduced is termed a ''[[hypostatic object]]''. |
| − | The above definition is adapted from the one given by [[Charles Sanders Peirce]] (CP 4.235, "The Simplest Mathematics" (1902), in ''Collected Papers'', CP 4.227–323). | + | The above definition is adapted from the one given by [[introduced by::Charles Sanders Peirce]] (CP 4.235, "[[introduced in::The Simplest Mathematics]]" (1902), in ''Collected Papers'', CP 4.227–323). |
| − | The way that Peirce describes it, the main thing about the formal operation of hypostatic abstraction, insofar as it can be observed to operate on formal linguistic expressions, is that it converts an adjective or some part of a predicate into an extra subject, upping the ''[[arity]]'', also called the ''adicity'', of the main predicate in the process. | + | The way that Peirce describes it, the main thing about the formal operation of hypostatic abstraction, insofar as it can be observed to operate on formal linguistic expressions, is that it converts an adjective or some part of a predicate into an extra [[subject]], upping the ''[[changes::arity of the main predicate|arity]]'', also called the ''[[changes::adicity]]'', of the main predicate in the process. |
| − | For example, a typical case of hypostatic abstraction occurs in the transformation from "honey is sweet" to "honey possesses sweetness", which transformation can be viewed in the following variety of ways: | + | For example, a typical case of hypostatic abstraction occurs in the transformation from "honey is sweet" to "[[example::honey possesses sweetness]]", which transformation can be viewed in the following variety of ways: |
<br> | <br> | ||
| Line 19: | Line 19: | ||
* [[Charles Sanders Peirce|Peirce, C.S.]], ''Collected Papers of Charles Sanders Peirce'', vols. 1–6, [[Charles Hartshorne]] and [[Paul Weiss]] (eds.), vols. 7–8, [[Arthur W. Burks]] (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958. | * [[Charles Sanders Peirce|Peirce, C.S.]], ''Collected Papers of Charles Sanders Peirce'', vols. 1–6, [[Charles Hartshorne]] and [[Paul Weiss]] (eds.), vols. 7–8, [[Arthur W. Burks]] (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958. | ||
| − | == | + | ==Resources== |
| + | |||
| + | * [http://vectors.usc.edu/thoughtmesh/publish/146.php Hypostatic Abstraction → ThoughtMesh] | ||
| + | |||
| + | * [http://web.clas.ufl.edu/users/jzeman/peirce_on_abstraction.htm J. Jay Zeman, ''Peirce on Abstraction''] | ||
| + | |||
| + | ==Syllabus== | ||
| + | |||
| + | ===Focal nodes=== | ||
| + | |||
| + | {{col-begin}} | ||
| + | {{col-break}} | ||
| + | * [[Inquiry Live]] | ||
| + | {{col-break}} | ||
| + | * [[Logic Live]] | ||
| + | {{col-end}} | ||
| + | |||
| + | ===Peer nodes=== | ||
| + | |||
| + | * [http://beta.wikiversity.org/wiki/Hypostatic_abstraction Hypostatic Abstraction @ Beta Wikiversity] | ||
| + | * [http://mywikibiz.com/Hypostatic_abstraction Hypostatic Abstraction @ MyWikiBiz] | ||
| + | * [http://www.netknowledge.org/wiki/Hypostatic_abstraction Hypostatic Abstraction @ NetKnowledge] | ||
| + | |||
| + | ===Logical operators=== | ||
| + | {{col-begin}} | ||
| + | {{col-break}} | ||
| + | * [[Exclusive disjunction]] | ||
| + | * [[Logical conjunction]] | ||
| + | * [[Logical disjunction]] | ||
| + | * [[Logical equality]] | ||
| + | {{col-break}} | ||
| + | * [[Logical implication]] | ||
| + | * [[Logical NAND]] | ||
| + | * [[Logical NNOR]] | ||
| + | * [[Logical negation|Negation]] | ||
| + | {{col-end}} | ||
| + | |||
| + | ===Related topics=== | ||
| + | |||
| + | {{col-begin}} | ||
| + | {{col-break}} | ||
| + | * [[Ampheck]] | ||
| + | * [[Boolean domain]] | ||
| + | * [[Boolean function]] | ||
| + | * [[Boolean-valued function]] | ||
| + | * [[Differential logic]] | ||
| + | {{col-break}} | ||
| + | * [[Logical graph]] | ||
| + | * [[Minimal negation operator]] | ||
| + | * [[Multigrade operator]] | ||
| + | * [[Parametric operator]] | ||
| + | * [[Peirce's law]] | ||
| + | {{col-break}} | ||
| + | * [[Propositional calculus]] | ||
| + | * [[Sole sufficient operator]] | ||
| + | * [[Truth table]] | ||
| + | * [[Universe of discourse]] | ||
| + | * [[Zeroth order logic]] | ||
| + | {{col-end}} | ||
| + | |||
| + | ===Relational concepts=== | ||
| + | |||
| + | {{col-begin}} | ||
| + | {{col-break}} | ||
* [[Continuous predicate]] | * [[Continuous predicate]] | ||
| − | * [[Hypostatic | + | * [[Hypostatic abstraction]] |
| − | * [[ | + | * [[Logic of relatives]] |
| + | * [[Logical matrix]] | ||
| + | {{col-break}} | ||
| + | * [[Relation (mathematics)|Relation]] | ||
| + | * [[Relation composition]] | ||
| + | * [[Relation construction]] | ||
| + | * [[Relation reduction]] | ||
| + | {{col-break}} | ||
| + | * [[Relation theory]] | ||
| + | * [[Relative term]] | ||
| + | * [[Sign relation]] | ||
| + | * [[Triadic relation]] | ||
| + | {{col-end}} | ||
| − | == | + | ===Related articles=== |
| + | |||
| + | * [http://mywikibiz.com/Directory:Jon_Awbrey/Papers/Propositional_Equation_Reasoning_Systems Jon Awbrey, “Propositional Equation Reasoning Systems”] | ||
| − | * [http:// | + | * [http://planetmath.org/encyclopedia/DifferentialPropositionalCalculus.html Jon Awbrey, “Differential Propositional Calculus”] |
| − | * [http:// | + | * [http://mywikibiz.com/Directory:Jon_Awbrey/Papers/Differential_Logic_:_Introduction Jon Awbrey, “Differential Logic : Introduction”] |
==Document history== | ==Document history== | ||
| Line 56: | Line 133: | ||
[[Category:Logic]] | [[Category:Logic]] | ||
[[Category:Mathematics]] | [[Category:Mathematics]] | ||
| + | [[Category:Philosophy]] | ||
[[Category:Semiotics]] | [[Category:Semiotics]] | ||
| − | |||
Revision as of 16:18, 29 April 2010
Hypostatic abstraction is a formal operation that takes an element of information, as expressed in a proposition \(X\ \operatorname{is}\ Y,\) and conceives its information to consist in the relation between that subject and another subject, as expressed in the proposition \(X\ \operatorname{has}\ Y\!\operatorname{-ness}.\) The existence of the abstract subject \(Y\!\operatorname{-ness}\) consists solely in the truth of those propositions that contain the concrete predicate \(Y.\!\) Hypostatic abstraction is known under many names, for example, hypostasis, objectification, reification, and subjectal abstraction. The object of discussion or thought thus introduced is termed a hypostatic object.
The above definition is adapted from the one given by Charles Sanders Peirce (CP 4.235, "The Simplest Mathematics" (1902), in Collected Papers, CP 4.227–323).
The way that Peirce describes it, the main thing about the formal operation of hypostatic abstraction, insofar as it can be observed to operate on formal linguistic expressions, is that it converts an adjective or some part of a predicate into an extra subject, upping the arity, also called the adicity, of the main predicate in the process.
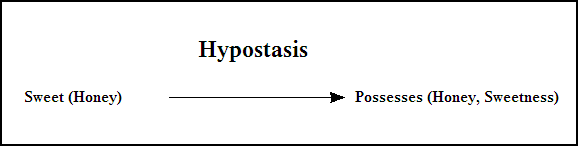
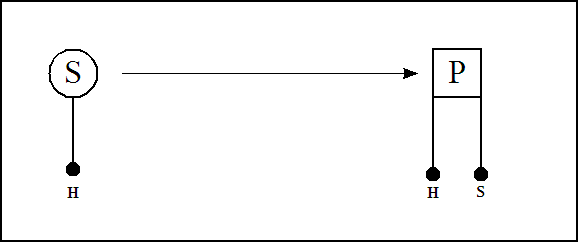
For example, a typical case of hypostatic abstraction occurs in the transformation from "honey is sweet" to "honey possesses sweetness", which transformation can be viewed in the following variety of ways:
The grammatical trace of this hypostatic transformation tells of a process that abstracts the adjective "sweet" from the main predicate "is sweet", thus arriving at a new, increased-arity predicate "possesses", and as a by-product of the reaction, as it were, precipitating out the substantive "sweetness" as a new second subject of the new predicate, "possesses".
References
- Peirce, C.S., Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958.
Resources
Syllabus
Focal nodes
Template:Col-breakTemplate:Col-breakTemplate:Col-endPeer nodes
- Hypostatic Abstraction @ Beta Wikiversity
- Hypostatic Abstraction @ MyWikiBiz
- Hypostatic Abstraction @ NetKnowledge
Logical operators
Related topics
- Propositional calculus
- Sole sufficient operator
- Truth table
- Universe of discourse
- Zeroth order logic
Relational concepts
Related articles
Document history
Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.
- Hypostatic Abstraction, MyWikiBiz
- Hypostatic Abstraction, Beta Wikiversity
- Hypostatic Abstraction, NetKnowledge
- Hypostatic Abstraction, PlanetMath
- Hypostatic Abstraction, Google Knol
- Hypostatic Abstraction, ThoughtMesh
- Hypostatic Abstraction, GetWiki
- Hypostatic Abstraction, Wikinfo
- Hypostatic Abstraction, Textop Wiki
- Hypostatic Abstraction, Wikipedia
<sharethis />