Difference between revisions of "Directory talk:Jon Awbrey/Papers/Differential Propositional Calculus"
Jon Awbrey (talk | contribs) (→Work Area: HTML --> TeX) |
Jon Awbrey (talk | contribs) (→Work Area: HTML --> TeX) |
||
| Line 1,416: | Line 1,416: | ||
| <math>A\!</math> | | <math>A\!</math> | ||
| | | | ||
| − | + | <math>\langle \mathcal{A} \rangle</math><br> | |
| − | + | <math>\langle a_1, \ldots, a_n \rangle</math><br> | |
| − | + | <math>\{ (a_1, \ldots, a_n) \}\!</math> | |
<math>A_1 \times \ldots \times A_n</math><br> | <math>A_1 \times \ldots \times A_n</math><br> | ||
<math>\prod_i A_i\!</math> | <math>\prod_i A_i\!</math> | ||
| Line 1,452: | Line 1,452: | ||
| | | | ||
<math>(\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B}))</math><br> | <math>(\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B}))</math><br> | ||
| − | <math>(\mathbb{B}^n + \to \mathbb{B})</math><br> | + | <math>(\mathbb{B}^n\ +\!\to \mathbb{B})</math><br> |
<math>[\mathbb{B}^n]</math> | <math>[\mathbb{B}^n]</math> | ||
|} | |} | ||
<br> | <br> | ||
Revision as of 22:44, 17 May 2008
Current Version @ PlanetMath : TeX Format
\PMlinkescapephrase{calculus}
\PMlinkescapephrase{Calculus}
\PMlinkescapephrase{circle}
\PMlinkescapephrase{Circle}
\PMlinkescapephrase{collection}
\PMlinkescapephrase{Collection}
\PMlinkescapephrase{cut}
\PMlinkescapephrase{Cut}
\PMlinkescapephrase{divides}
\PMlinkescapephrase{Divides}
\PMlinkescapephrase{language}
\PMlinkescapephrase{Language}
\PMlinkescapephrase{object}
\PMlinkescapephrase{Object}
\PMlinkescapephrase{parallel}
\PMlinkescapephrase{Parallel}
\PMlinkescapephrase{place}
\PMlinkescapephrase{Place}
\PMlinkescapephrase{representation}
\PMlinkescapephrase{Representation}
\PMlinkescapephrase{represents}
\PMlinkescapephrase{Represents}
\PMlinkescapephrase{simple}
\PMlinkescapephrase{Simple}
A \textbf{differential propositional calculus} is a \PMlinkname{propositional calculus}{PropositionalCalculus} extended by a set of terms for describing aspects of change and difference, for example, processes that take place in a universe of discourse or transformations that map a source universe into a target universe.
\tableofcontents
\section{Casual introduction}
Consider the situation represented by the venn diagram in Figure 1.
\begin{figure}[h]\begin{centering}
\begin{footnotesize}\begin{verbatim}
o-----------------------------------------------------------o
| X . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . o-------------o . . . . . . . . . . . . . . . |
| . . h . . ./. . . . . . . .\. . . . . . . . . . . . . . . |
| . . @ . . / . . . . . . . . \ . . . . . . . . . . . . . . |
| . . . . ./. . i . . . . . . .\. . . . . . . . . . . . . . |
| . . . . / . . @ . . . . . . . \ . . . . . . . . . . . . . |
| . . . ./. . . . . . . . . . . .\. . . . . . . . . . . . . |
| . . . o . . . . . . . . . . j . o . . . . . . . . . . . . |
| . . . | . . . . . . . . . . @ . | . . . . . . . . . . . . |
| . . . | . . . . . . . . . . . . | . . . . . . . . . . . . |
| . . . | . . . . . .Q. . . . . . | . . . . . . . . . . . . |
| . . . | . . . . . . . . . . . . | . . . . . k . . . . . . |
| . . . | . . . . . . . . . . . . | . . . . . @ . . . . . . |
| . . . o . . . . . . . . . . . . o . . . . . . . . . . . . |
| . . . .\. . . . . . . . . . . ./. . . . . . . . . . . . . |
| . . . . \ . . . . . . . . . . / . . . . . . . . . . . . . |
| . . . . .\. . . . . . . . . ./. . . . . . . . . . . . . . |
| . . . . . \ . . . . . . . . / . . . . . . . . . . . . . . |
| . . . . . .\. . . . . . . ./. . . . . . . . . . . . . . . |
| . . . . . . o-------------o . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
o-----------------------------------------------------------o
\end{verbatim}\end{footnotesize}
Figure 1. Local Habitations, And Names
\end{centering}\end{figure}
The area of the rectangle represents a universe of discourse, $X.$ This might be a population of individuals having various additional properties or it might be a collection of locations that various individuals occupy. The area of the ``circle" represents the individuals that have the property $q$ or the locations that fall within the corresponding region $Q.$ Four individuals, $h, i, j, k,$ are singled out by name. It happens that $i$ and $j$ currently reside in region $Q$ while $h$ and $k$ do not.
Now consider the situation represented by the venn diagram in Figure 2.
\begin{figure}[h]\begin{centering}
\begin{footnotesize}\begin{verbatim}
o-----------------------------------------------------------o
| X . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . o-------------o . . . . . . . . . . . . . . . |
| . . h . . ./. . . . . . . .\. . . . . . . . . . . . . . . |
| . . @ . . / . . . . . . . . \ . . . . . . . . . . . . . . |
| . . . . ./. . i . . . . . . .\. . . . . . . . . . . . . . |
| . . . . / . . @ . . . . . . . \ . . . . . . . . . . . . . |
| . . . ./. . . . . . . . . . . .\. . . . . . . . . . . . . |
| . . . o . . . . . . . . . . . . o . . . . . j . . . . . . |
| . . . | . . . . . . . . . . . . | . . . . . @ . . . . . . |
| . . . | . . . . . . . . . . . . | . . . . . . . . . . . . |
| . . . | . . . . . .Q. . . . . . | . . . . . . . . . . . . |
| . . . | . . . . . . . . . . k . | . . . . . . . . . . . . |
| . . . | . . . . . . . . . . @ . | . . . . . . . . . . . . |
| . . . o . . . . . . . . . . . . o . . . . . . . . . . . . |
| . . . .\. . . . . . . . . . . ./. . . . . . . . . . . . . |
| . . . . \ . . . . . . . . . . / . . . . . . . . . . . . . |
| . . . . .\. . . . . . . . . ./. . . . . . . . . . . . . . |
| . . . . . \ . . . . . . . . / . . . . . . . . . . . . . . |
| . . . . . .\. . . . . . . ./. . . . . . . . . . . . . . . |
| . . . . . . o-------------o . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
o-----------------------------------------------------------o
\end{verbatim}\end{footnotesize}
Figure 2. Same Names, Different Habitations
\end{centering}\end{figure}
Figure 2 differs from Figure 1 solely in the circumstance that the object $j$ is outside the region $Q$ while the object $k$ is inside the region $Q.$ So far, there is nothing that says that our encountering these Figures in this order is other than purely accidental, but if we interpret the present sequence of frames as a ``moving picture" representation of their natural order in a temporal process, then it would be natural to say that $h$ and $i$ have remained as they were with regard to quality $q$ while $j$ and $k$ have changed their standings in that respect. In particular, $j$ has moved from the region where $q$ is $\textsl{true}$ to the region where $q$ is $\textsl{false}$ while $k$ has moved from the region where $q$ is $\textsl{false}$ to the region where $q$ is $\textsl{true}.$
Figure $1^\prime$ reprises the situation shown in Figure 1, but this time interpolates a new quality that is specifically tailored to account for the relation between Figure 1 and Figure 2.
\begin{figure}[h]\begin{centering}
\begin{footnotesize}\begin{verbatim}
o-----------------------------------------------------------o
| X . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . o-------------o . o-------------o . . . . . . |
| . . h . . ./. . . . . . . .\./. . . . . . . .\. . . . . . |
| . . @ . . / . . . . . . . . o . . . . . . . . \ . . . . . |
| . . . . ./. . i . . . . . ./.\. . . . . . . . .\. . . . . |
| . . . . / . . @ . . . . . / . \ . . . . . . . . \ . . . . |
| . . . ./. . . . . . . . ./. . .\. . . . . . . . .\. . . . |
| . . . o . . . . . . . . o . j . o . . . . . . . . o . . . |
| . . . | . . . . . . . . | . @ . | . . . . . . . . | . . . |
| . . . | . . . . . . . . | . . . | . . . . . . . . | . . . |
| . . . | . . . . . Q . . | . . . | . . dQ. . . . . | . . . |
| . . . | . . . . . . . . | . . . | . . . . . k . . | . . . |
| . . . | . . . . . . . . | . . . | . . . . . @ . . | . . . |
| . . . o . . . . . . . . o . . . o . . . . . . . . o . . . |
| . . . .\. . . . . . . . .\. . ./. . . . . . . . ./. . . . |
| . . . . \ . . . . . . . . \ . / . . . . . . . . / . . . . |
| . . . . .\. . . . . . . . .\./. . . . . . . . ./. . . . . |
| . . . . . \ . . . . . . . . o . . . . . . . . / . . . . . |
| . . . . . .\. . . . . . . ./.\. . . . . . . ./. . . . . . |
| . . . . . . o-------------o . o-------------o . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
o-----------------------------------------------------------o
\end{verbatim}\end{footnotesize}
Figure $1^\prime$. Back, To The Future
\end{centering}\end{figure}
This new quality, $\operatorname{d}q,$ is an example of a \textit{differential quality}, since its absence or presence qualifies the absence or presence of change occurring in another quality. As with any other quality, it is represented in the venn diagram by means of a ``circle" that distinguishes two halves of the universe of discourse, in this case, the portions of $X$ outside and inside the region $\operatorname{d}Q.$
Figure 1 represents a universe of discourse, $X,$ together with a basis of discussion, $\{ q \},$ for expressing propositions about the contents of that universe. Once the quality $q$ is given a name, say, the symbol $``q"$, we have a basis for a formal language that is specifically cut out for discussing $X$ in terms of $q,$ and this formal language is more formally known as the \textit{propositional calculus} with alphabet $\{ ``q" \}.$
In the context marked by $X$ and $\{ q \}$ there are but four different pieces of information that can be expressed in the corresponding propositional calculus, namely, the propositions: $\textsl{false},\ \lnot q,\ q,\ \textsl{true}.$ Referring to the sample of points in Figure 1, $\textsl{false}$ holds of no points, $\lnot q$ holds of $h$ and $k$, $q$ holds of $i$ and $j$, and $\textsl{true}$ holds of all points in the sample.
Figure $1^\prime$ preserves the same universe of discourse and extends the basis of discussion to a set of two qualities, $\{ q,\ \operatorname{d}q \}.$ In parallel fashion, the initial propositional calculus is extended by means of the enlarged alphabet, $\{ ``q", ``\operatorname{d}q" \}.$ Any propositional calculus over two basic propositions allows for the expression of 16 propositions all together. Just by way of salient examples in the present setting, we can pick out the most informative propositions that apply to each of our sample points. Using overlines to express logical negation, these are given as follows:
\begin{itemize}
\item
$\overline{q}\ \overline{\operatorname{d}q}$ describes $h$
\item
$\overline{q}\ \operatorname{d}q$ describes $k$
\item
$q\ \overline{\operatorname{d}q}$ describes $i$
\item
$q\ \operatorname{d}q$ describes $j$
\end{itemize}
Table 3 exhibits the rules of inference that give the differential quality $\operatorname{d}q$ its meaning in practice.
\begin{center}\begin{tabular}{ccccccc}
\multicolumn{7}{c}{Table 3. Differential Inference Rules} \\[12pt]
From & $\overline{q}$ & and & $\overline{\operatorname{d}q}$ & infer & $\overline{q}$ & next. \\[6pt]
From & $\overline{q}$ & and & $\operatorname{d}q$ & infer & $q$ & next. \\[6pt]
From & $q$ & and & $\overline{\operatorname{d}q}$ & infer & $q$ & next. \\[6pt]
From & $q$ & and & $\operatorname{d}q$ & infer & $\overline{q}$ & next. \\[6pt]
\end{tabular}\end{center}
$\ldots$
\section{Formal development}
$\ldots$
\section{Expository examples}
$\ldots$
Draft Conversion @ MyWikiBiz : Wiki Format
A differential propositional calculus is a propositional calculus extended by a set of terms for describing aspects of change and difference, for example, processes that take place in a universe of discourse or transformations that map a source universe into a target universe.
Casual introduction
Consider the situation represented by the venn diagram in Figure 1.
o-----------------------------------------------------------o | X . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . o-------------o . . . . . . . . . . . . . . . | | . . h . . ./. . . . . . . .\. . . . . . . . . . . . . . . | | . . @ . . / . . . . . . . . \ . . . . . . . . . . . . . . | | . . . . ./. . i . . . . . . .\. . . . . . . . . . . . . . | | . . . . / . . @ . . . . . . . \ . . . . . . . . . . . . . | | . . . ./. . . . . . . . . . . .\. . . . . . . . . . . . . | | . . . o . . . . . . . . . . j . o . . . . . . . . . . . . | | . . . | . . . . . . . . . . @ . | . . . . . . . . . . . . | | . . . | . . . . . . . . . . . . | . . . . . . . . . . . . | | . . . | . . . . . .Q. . . . . . | . . . . . . . . . . . . | | . . . | . . . . . . . . . . . . | . . . . . k . . . . . . | | . . . | . . . . . . . . . . . . | . . . . . @ . . . . . . | | . . . o . . . . . . . . . . . . o . . . . . . . . . . . . | | . . . .\. . . . . . . . . . . ./. . . . . . . . . . . . . | | . . . . \ . . . . . . . . . . / . . . . . . . . . . . . . | | . . . . .\. . . . . . . . . ./. . . . . . . . . . . . . . | | . . . . . \ . . . . . . . . / . . . . . . . . . . . . . . | | . . . . . .\. . . . . . . ./. . . . . . . . . . . . . . . | | . . . . . . o-------------o . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | o-----------------------------------------------------------o
Figure 1. Local Habitations, And Names
The area of the rectangle represents a universe of discourse, \(X.\!\) This might be a population of individuals having various additional properties or it might be a collection of locations that various individuals occupy. The area of the "circle" represents the individuals that have the property \(q\!\) or the locations that fall within the corresponding region \(Q.\!\) Four individuals, \(h, i, j, k,\!\) are singled out by name. It happens that \(i\!\) and \(j\!\) currently reside in region \(Q\!\) while \(h\!\) and \(k\!\) do not.
Now consider the situation represented by the venn diagram in Figure 2.
o-----------------------------------------------------------o | X . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . o-------------o . . . . . . . . . . . . . . . | | . . h . . ./. . . . . . . .\. . . . . . . . . . . . . . . | | . . @ . . / . . . . . . . . \ . . . . . . . . . . . . . . | | . . . . ./. . i . . . . . . .\. . . . . . . . . . . . . . | | . . . . / . . @ . . . . . . . \ . . . . . . . . . . . . . | | . . . ./. . . . . . . . . . . .\. . . . . . . . . . . . . | | . . . o . . . . . . . . . . . . o . . . . . j . . . . . . | | . . . | . . . . . . . . . . . . | . . . . . @ . . . . . . | | . . . | . . . . . . . . . . . . | . . . . . . . . . . . . | | . . . | . . . . . .Q. . . . . . | . . . . . . . . . . . . | | . . . | . . . . . . . . . . k . | . . . . . . . . . . . . | | . . . | . . . . . . . . . . @ . | . . . . . . . . . . . . | | . . . o . . . . . . . . . . . . o . . . . . . . . . . . . | | . . . .\. . . . . . . . . . . ./. . . . . . . . . . . . . | | . . . . \ . . . . . . . . . . / . . . . . . . . . . . . . | | . . . . .\. . . . . . . . . ./. . . . . . . . . . . . . . | | . . . . . \ . . . . . . . . / . . . . . . . . . . . . . . | | . . . . . .\. . . . . . . ./. . . . . . . . . . . . . . . | | . . . . . . o-------------o . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | o-----------------------------------------------------------o
Figure 2. Same Names, Different Habitations
Figure 2 differs from Figure 1 solely in the circumstance that the object \(j\!\) is outside the region \(Q\!\) while the object \(k\!\) is inside the region \(Q.\!\) So far, there is nothing that says that our encountering these Figures in this order is other than purely accidental, but if we interpret the present sequence of frames as a "moving picture" representation of their natural order in a temporal process, then it would be natural to say that \(h\!\) and \(i\!\) have remained as they were with regard to quality \(q\!\) while \(j\!\) and \(k\!\) have changed their standings in that respect. In particular, \(j\!\) has moved from the region where \(q\!\) is \(true\!\) to the region where \(q\!\) is \(false\!\) while \(k\!\) has moved from the region where \(q\!\) is \(false\!\) to the region where \(q\!\) is \(true.\!\)
Figure 1′ reprises the situation shown in Figure 1, but this time interpolates a new quality that is specifically tailored to account for the relation between Figure 1 and Figure 2.
o-----------------------------------------------------------o | X . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . o-------------o . o-------------o . . . . . . | | . . h . . ./. . . . . . . .\./. . . . . . . .\. . . . . . | | . . @ . . / . . . . . . . . o . . . . . . . . \ . . . . . | | . . . . ./. . i . . . . . ./.\. . . . . . . . .\. . . . . | | . . . . / . . @ . . . . . / . \ . . . . . . . . \ . . . . | | . . . ./. . . . . . . . ./. . .\. . . . . . . . .\. . . . | | . . . o . . . . . . . . o . j . o . . . . . . . . o . . . | | . . . | . . . . . . . . | . @ . | . . . . . . . . | . . . | | . . . | . . . . . . . . | . . . | . . . . . . . . | . . . | | . . . | . . . . . Q . . | . . . | . . dQ. . . . . | . . . | | . . . | . . . . . . . . | . . . | . . . . . k . . | . . . | | . . . | . . . . . . . . | . . . | . . . . . @ . . | . . . | | . . . o . . . . . . . . o . . . o . . . . . . . . o . . . | | . . . .\. . . . . . . . .\. . ./. . . . . . . . ./. . . . | | . . . . \ . . . . . . . . \ . / . . . . . . . . / . . . . | | . . . . .\. . . . . . . . .\./. . . . . . . . ./. . . . . | | . . . . . \ . . . . . . . . o . . . . . . . . / . . . . . | | . . . . . .\. . . . . . . ./.\. . . . . . . ./. . . . . . | | . . . . . . o-------------o . o-------------o . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | o-----------------------------------------------------------o
Figure 1′. Back, To The Future
This new quality, \(\operatorname{d}q,\!\) is an example of a differential quality, since its absence or presence qualifies the absence or presence of change occurring in another quality. As with any other quality, it is represented in the venn diagram by means of a "circle" that distinguishes two halves of the universe of discourse, in this case, the portions of \(X\!\) outside and inside the region \(\operatorname{d}Q.\!\)
Figure 1 represents a universe of discourse, \(X,\!\) together with a basis of discussion, \(\{ q \},\!\) for expressing propositions about the contents of that universe. Once the quality \(q\!\) is given a name, say, the symbol "\(q\!\)", we have the basis for a formal language that is specifically cut out for discussing \(X\!\) in terms of \(q,\!\) and this formal language is more formally known as the propositional calculus with alphabet \(\{\!\)"\(q\!\)"\(\}.\!\)
In the context marked by \(X\!\) and \(\{ q \}\!\) there are but four different pieces of information that can be expressed in the corresponding propositional calculus, namely, the propositions\[false,\!\] \(\lnot q,\!\) \(q,\!\) \(true.\!\) Referring to the sample of points in Figure 1, \(false\!\) holds of no points, \(\lnot q\!\) holds of \(h\!\) and \(k,\!\) \(q\!\) holds of \(i\!\) and \(j,\!\) and \(true\!\) holds of all points in the sample.
Figure 1′ preserves the same universe of discourse and extends the basis of discussion to a set of two qualities, \(\{ q, \operatorname{d}q \}.\!\) In parallel fashion, the initial propositional calculus is extended by means of the enlarged alphabet, \(\{\!\)"\(q\!\)"\(,\!\) "\(\operatorname{d}q\!\)"\(\}.\!\) Any propositional calculus over two basic propositions allows for the expression of 16 propositions all together. Just by way of salient examples in the present setting, we can pick out the most informative propositions that apply to each of our sample points. Using overlines to express logical negation, these are given as follows:
\(\overline{q}\ \overline{\operatorname{d}q}\) describes \(h\!\)
\(\overline{q}\ \operatorname{d}q\) describes \(k\!\)
\(q\ \overline{\operatorname{d}q}\) describes \(i\!\)
\(q\ \operatorname{d}q\) describes \(j\!\)
Table 3 exhibits the rules of inference that give the differential quality \(\operatorname{d}q\!\) its meaning in practice.
|
…
Formal development
…
Expository examples
…
Materials from "Dif Log Dyn Sys" for Reuse Here
Excerpts from "Differential Logic and Dynamic Systems"
A Functional Conception of Propositional Calculus
Out of the dimness opposite equals advance . . . .
Always substance and increase,
Always a knit of identity . . . . always distinction . . . .
always a breed of life.Walt Whitman, Leaves of Grass, [Whi, 28]
In the general case, we start with a set of logical features {a1, …, an} that represent properties of objects or propositions about the world. In concrete examples the features {ai} commonly appear as capital letters from an alphabet like {A, B, C, …} or as meaningful words from a linguistic vocabulary of codes. This language can be drawn from any sources, whether natural, technical, or artificial in character and interpretation. In the application to dynamic systems we tend to use the letters {x1, …, xn} as our coordinate propositions, and to interpret them as denoting properties of a system's state, that is, as propositions about its location in configuration space. Because I have to consider non-deterministic systems from the outset, I often use the word state in a loose sense, to denote the position or configuration component of a contemplated state vector, whether or not it ever gets a deterministic completion.
The set of logical features {a1, …, an} provides a basis for generating an n-dimensional universe of discourse that I denote as [a1, …, an]. It is useful to consider each universe of discourse as a unified categorical object that incorporates both the set of points 〈a1, …, an〉 and the set of propositions f : 〈a1, …, an〉 → B that are implicit with the ordinary picture of a venn diagram on n features. Thus, we may regard the universe of discourse [a1, …, an] as an ordered pair having the type (Bn, (Bn → B), and we may abbreviate this last type designation as Bn +→ B, or even more succinctly as [Bn]. (Used this way, the angle brackets 〈…〉 are referred to as generator brackets.)
Table 2 exhibits the scheme of notation I use to formalize the domain of propositional calculus, corresponding to the logical content of truth tables and venn diagrams. Although it overworks the square brackets a bit, I also use either one of the equivalent notations [n] or n to denote the data type of a finite set on n elements.
| Symbol | Notation | Description | Type |
|---|---|---|---|
| A | {a1, …, an} | Alphabet | [n] = n |
| Ai | {(ai), ai} | Dimension i | B |
| A |
〈A〉 |
Set of cells, |
Bn |
| A* | (hom : A → B) | Linear functions | (Bn)* = Bn |
| A^ | (A → B) | Boolean functions | Bn → B |
| A• |
[A] |
Universe of discourse |
(Bn, (Bn → B)) |
Reality at the Threshold of Logic
But no science can rest entirely on measurement, and many scientific investigations are quite out of reach of that device. To the scientist longing for non-quantitative techniques, then, mathematical logic brings hope.
W.V. Quine, Mathematical Logic, [Qui, 7]
Table 5 accumulates an array of notation that I hope will not be too distracting. Some of it is rarely needed, but has been filled in for the sake of completeness. Its purpose is simple, to give literal expression to the visual intuitions that come with venn diagrams, and to help build a bridge between our qualitative and quantitative outlooks on dynamic systems.
| Linear Space | Liminal Space | Logical Space |
|---|---|---|
|
X |
X |
A |
|
Xi |
Xi |
Ai |
|
X |
X |
A |
|
X* |
X* |
A* |
|
X^ |
X^ |
A^ |
|
X• |
X• |
A• |
The left side of the Table collects mostly standard notation for an n-dimensional vector space over a field K. The right side of the table repeats the first elements of a notation that I sketched above, to be used in further developments of propositional calculus. (I plan to use this notation in the logical analysis of neural network systems.) The middle column of the table is designed as a transitional step from the case of an arbitrary field K, with a special interest in the continuous line R, to the qualitative and discrete situations that are instanced and typified by B.
I now proceed to explain these concepts in more detail. The two most important ideas developed in the table are:
- The idea of a universe of discourse, which includes both a space of points and a space of maps on those points.
- The idea of passing from a more complex universe to a simpler universe by a process of thresholding each dimension of variation down to a single bit of information.
For the sake of concreteness, let us suppose that we start with a continuous n-dimensional vector space like X = 〈x1, …, xn〉 \(\cong\) Rn. The coordinate system X = {xi} is a set of maps xi : Rn → R, also known as the coordinate projections. Given a "dataset" of points x in Rn, there are numerous ways of sensibly reducing the data down to one bit for each dimension. One strategy that is general enough for our present purposes is as follows. For each i we choose an n-ary relation Li on R, that is, a subset of Rn, and then we define the ith threshold map, or limen xi as follows:
- xi : Rn → B such that:
- xi(x) = 1 if x ∈ Li,
- xi(x) = 0 if otherwise.
In other notations that are sometimes used, the operator \(\chi (\ )\) or the corner brackets \(\lceil \ldots \rceil\) can be used to denote a characteristic function, that is, a mapping from statements to their truth values, given as elements of B. Finally, it is not uncommon to use the name of the relation itself as a predicate that maps n-tuples into truth values. In each of these notations, the above definition could be expressed as follows:
- xi(x) = \(\chi (x \in L_i)\) = \(\lceil x \in L_i \rceil\) = Li(x).
Notice that, as defined here, there need be no actual relation between the n-dimensional subsets {Li} and the coordinate axes corresponding to {xi}, aside from the circumstance that the two sets have the same cardinality. In concrete cases, though, one usually has some reason for associating these "volumes" with these "lines", for instance, Li is bounded by some hyperplane that intersects the ith axis at a unique threshold value ri ∈ R. Often, the hyperplane is chosen normal to the axis. In recognition of this motive, let us make the following convention. When the set Li has points on the ith axis, that is, points of the form ‹0, …, 0, ri, 0, …, 0› where only the xi coordinate is possibly non-zero, we may pick any one of these coordinate values as a parametric index of the relation. In this case we say that the indexing is real, otherwise the indexing is imaginary. For a knowledge based system X, this should serve once again to mark the distinction between acquaintance and opinion.
States of knowledge about the location of a system or about the distribution of a population of systems in a state space X = Rn can now be expressed by taking the set X = {xi} as a basis of logical features. In picturesque terms, one may think of the underscore and the subscript as combining to form a subtextual spelling for the ith threshold map. This can help to remind us that the threshold operator )i acts on x by setting up a kind of a "hurdle" for it. In this interpretation, the coordinate proposition xi asserts that the representative point x resides above the ith threshold.
Primitive assertions of the form xi(x) can then be negated and joined by means of propositional connectives in the usual ways to provide information about the state x of a contemplated system or a statistical ensemble of systems. Parentheses "( )" may be used to indicate negation. Eventually one discovers the usefulness of the k-ary just one false operators of the form "( , , , )", as treated in earlier reports. This much tackle generates a space of points (cells, interpretations), X = 〈X〉 \(\cong\) Bn, and a space of functions (regions, propositions), X^ \(\cong\) (Bn → B). Together these form a new universe of discourse X • = [X] of the type (Bn, (Bn → B)), which we may abbreviate as Bn +→ B, or most succinctly as [Bn].
The square brackets have been chosen to recall the rectangular frame of a venn diagram. In thinking about a universe of discourse it is a good idea to keep this picture in mind, where we constantly think of the elementary cells x, the defining features xi, and the potential shadings f : X → B, all at the same time, remaining aware of the arbitrariness of the way that we choose to inscribe our distinctions in the medium of a continuous space.
Finally, let X* denote the space of linear functions, (hom : X → K), which in the finite case has the same dimensionality as X, and let the same notation be extended across the table.
We have just gone through a lot of work, apparently doing nothing more substantial than spinning a complex spell of notational devices through a labyrinth of baffled spaces and baffling maps. The reason for doing this was to bind together and to constitute the intuitive concept of a universe of discourse into a coherent categorical object, the kind of thing, once grasped, which can be turned over in the mind and considered in all its manifold changes and facets. The effort invested in these preliminary measures is intended to pay off later, when we need to consider the state transformations and the time evolution of neural network systems.
Back to the Beginning : Some Exemplary Universes
I would have preferred to be enveloped in words,
borne way beyond all possible beginnings.Michel Foucault, The Discourse on Language, [Fou, 215]
To anchor our understanding of differential logic, let us look at how the various concepts apply in the simplest possible concrete cases, where the initial dimension is only 1 or 2. In spite of the obvious simplicity of these cases, it is possible to observe how central difficulties of the subject begin to arise already at this stage.
A One-Dimensional Universe
There was never any more inception than there is now,
Nor any more youth or age than there is now;
And will never be any more perfection than there is now,
Nor any more heaven or hell than there is now.Walt Whitman, Leaves of Grass, [Whi, 28]
Let X = {x1} = {A} be an alphabet that represents one boolean variable or a single logical feature. In this example I am using the capital letter "A" in a more usual informal way, to name a feature and not a space, at variance with my formerly stated formal conventions. At any rate, the basis element A = x1 may be interpreted as a simple proposition or a coordinate projection A = x1 : B1 ¸> B. The space X = 〈A 〉 = {(A), A} of points (cells, vectors, interpretations) has cardinality 2n = 21 = 2 and is isomorphic to B = {0, 1}. Moreover, X may be identified with the set of singular propositions {x : B ××> B}. The space of linear propositions X* = {hom : B +> B} = {0, A} is algebraically dual to X and also has cardinality 2. Here, "0" is interpreted as denoting the constant function 0 : B → B, amounting to the linear proposition of rank 0, while A is the linear proposition of rank 1. Last but not least we have the positive propositions {pos : B ¥> B} = {A, 1}, of rank 1 and 0, respectively, where "1" is understood as denoting the constant function 1 : B → B. In sum, there are \(2^{2^n} = 2^{2^1} = 4\) propositions altogether in the universe of discourse, comprising the set X^ = {f : X → B} = {0, (A), A, 1} \(\cong\) (B → B).
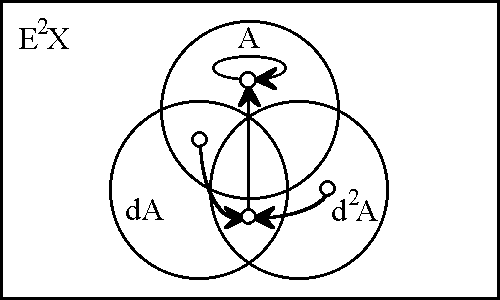
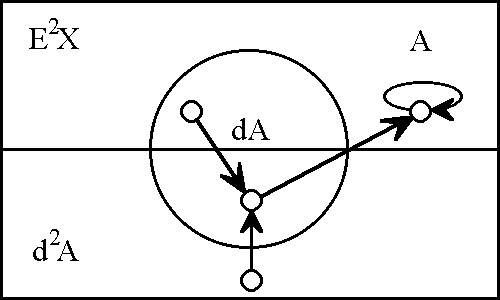
The first order differential extension of X is EX = {x1, dx1} = {A, dA}. If the feature "A" is understood as applying to some object or state, then the feature "dA" may be interpreted as an attribute of the same object or state that says that it is changing significantly with respect to the property A, or that it has an escape velocity with respect to the state A. In practice, differential features acquire their logical meaning through a class of temporal inference rules.
For example, relative to a frame of observation that is left implicit for now, one is permitted to make the following sorts of inference: From the fact that A and dA are true at a given moment one may infer that (A) will be true in the next moment of observation. Altogether in the present instance, there is the fourfold scheme of inference that is shown below:
|
It might be thought that we need to bring in an independent time variable at this point, but an insight of fundamental importance appears to be that the idea of process is more basic than the notion of time. A time variable is actually a reference to a clock, that is, a canonical or a convenient process that is established or accepted as a standard of measurement, but in essence no different than any other process. This raises the question of how different subsystems in a more global process can be brought into comparison, and what it means for one process to serve the function of a local standard for others. But these inquiries only wrap up puzzles in further riddles, and are obviously too involved to be handled at our current level of approximation.
The clock indicates the moment . . . . but what does
eternity indicate?Walt Whitman, 'Leaves of Grass', [Whi, 79]
Observe that the secular inference rules, used by themselves, involve a loss of information, since nothing in them can tell us whether the momenta {(dA), dA} are preserved or changed in the next instance. In order to know this, we would have to determine d2A, and so on, pursuing an infinite regress. Ultimately, in order to rest with a finitely determinate system, it is necessary to make an infinite assumption, for example, that dkA = 0 for all k greater than some fixed value M. Another way to escape the regress is through the provision of a dynamic law, in typical form making higher order differentials dependent on lower degrees and estates.
Example 1. A Square Rigging
Urge and urge and urge,
Always the procreant urge of the world.Walt Whitman, Leaves of Grass, [Whi, 28]
By way of example, suppose that we are given the initial condition A = dA and the law d2A = (A). Then, since "A = dA" ⇔ "A dA or (A)(dA)", we may infer two possible trajectories, as displayed in Table 11. In either of these cases, the state A(dA)(d2A) is a stable attractor or a terminal condition for both starting points.
| Time | Trajectory 1 | Trajectory 2 | |||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
Because the initial space X = 〈A〉 is one-dimensional, we can easily fit the second order extension E2X = 〈A, dA, d2A〉 within the compass of a single venn diagram, charting the couple of converging trajectories as shown in Figure 12.
If we eliminate from view the regions of E2X that are ruled out by the dynamic law d2A = (A), then what remains is the quotient structure that is shown in Figure 13. This picture makes it easy to see that the dynamically allowable portion of the universe is partitioned between the properties A and d2A. As it happens, this fact might have been expressed "right off the bat" by an equivalent formulation of the differential law, one that uses the exclusive disjunction to state the law as (A, d2A).
What we have achieved in this example is to give a differential description of a simple dynamic process. In effect, we did this by embedding a directed graph, which can be taken to represent the state transitions of a finite automaton, in a dynamically allotted quotient structure that is created from a boolean lattice or an n-cube by nullifying all of the regions that the dynamics outlaws. With growth in the dimensions of our contemplated universes, it becomes essential, both for human comprehension and for computer implementation, that the dynamic structures of interest to us be represented not actually, by acquaintance, but virtually, by description. In our present study, we are using the language of propositional calculus to express the relevant descriptions, and to comprehend the structure that is implicit in the subsets of a n-cube without necessarily being forced to actualize all of its points.
One of the reasons for engaging in this kind of extremely reduced, but explicitly controlled case study is to throw light on the general study of languages, formal and natural, in their full array of syntactic, semantic, and pragmatic aspects. Propositional calculus is one of the last points of departure where we can view these three aspects interacting in a non-trivial way without being immediately and totally overwhelmed by the complexity they generate. Often this complexity causes investigators of formal and natural languages to adopt the strategy of focusing on a single aspect and to abandon all hope of understanding the whole, whether it's the still living natural language or the dynamics of inquiry that lies crystallized in formal logic.
From the perspective that I find most useful here, a language is a syntactic system that is designed or evolved in part to express a set of descriptions. When the explicit symbols of a language have extensions in its object world that are actually infinite, or when the implicit categories and generative devices of a linguistic theory have extensions in its subject matter that are potentially infinite, then the finite characters of terms, statements, arguments, grammars, logics, and rhetorics force an excess of intension to reside in all these symbols and functions, across the spectrum from the object language to the metalinguistic uses. In the aphorism from W. von Humboldt that Chomsky often cites, for example, in [Cho86, 30] and [Cho93, 49], language requires "the infinite use of finite means". This is necessarily true when the extensions are infinite, when the referential symbols and grammatical categories of a language possess infinite sets of models and instances. But it also voices a practical truth when the extensions, though finite at every stage, tend to grow at exponential rates.
This consequence of dealing with extensions that are "practically infinite" becomes crucial when one tries to build neural network systems that learn, since the learning competence of any intelligent system is limited to the objects and domains that it is able to represent. If we want to design systems that operate intelligently with the full deck of propositions dealt by intact universes of discourse, then we must supply them with succinct representations and efficient transformations in this domain. Furthermore, in the project of constructing inquiry driven systems, we find ourselves forced to contemplate the level of generality that is embodied in propositions, because the dynamic evolution of these systems is driven by the measurable discrepancies that occur among their expectations, intentions, and observations, and because each of these subsystems or components of knowledge constitutes a propositional modality that can take on the fully generic character of an empirical summary or an axiomatic theory.
A compression scheme by any other name is a symbolic representation, and this is what the differential extension of propositional calculus, through all of its many universes of discourse, is intended to supply. Why is this particular program of mental calisthenics worth carrying out in general? By providing a uniform logical medium for describing dynamic systems we can make the task of understanding complex systems much easier, both in looking for invariant representations of individual cases and in finding points of comparison among diverse structures that would otherwise appear as isolated systems. All of this goes to facilitate the search for compact knowledge and to adapt what is learned from individual cases to the general realm.
Back to the Feature
I guess it must be the flag of my disposition, out of hopeful
green stuff woven.Walt Whitman, Leaves of Grass, [Whi, 31]
Let us assume that the sense intended for differential features is well enough established in the intuition, for now, that I may continue with outlining the structure of the differential extension [EX] = [A, dA]. Over the extended alphabet EX = {x1, dx1} = {A, dA}, of cardinality 2n = 2, we generate the set of points, EX, of cardinality 22n = 4, that bears the following chain of equivalent descriptions:
EX = 〈A, dA〉 = {(A), A} × {(dA), dA} = {(A)(dA), (A) dA, A (dA), A dA}.
The space EX may be assigned the mnemonic type B × D, which is really no different than B × B = B2. An individual element of EX may be regarded as a disposition at a point or a situated direction, in effect, a singular mode of change occurring at a single point in the universe of discourse. In applications, the modality of this change can be interpreted in various ways, for example, as an expectation, an intention, or an observation with respect to the behavior of a system.
To complete the construction of the extended universe of discourse EX • = [x1, dx1] = [A, dA], one must add the set of differential propositions EX^ = {g : EX → B} \(\cong\) (B × D → B) to the set of dispositions in EX. There are \(2^{2^{2n}}\) = 16 propositions in EX^, as detailed in Table 14.
| A : | 1 1 0 0 | ||||||||||
| dA : | 1 0 1 0 | ||||||||||
| f0 | g0 | 0 0 0 0 | ( ) | False | 0 | ||||||
|
|
|
|
|
| ||||||
|
|
|
|
|
| ||||||
|
|
|
|
|
| ||||||
|
|
|
|
|
| ||||||
|
|
|
|
|
| ||||||
| f3 | g15 | 1 1 1 1 | (( )) | True | 1 |
Aside from changing the names of variables and shuffling the order of rows, this Table follows the format that was used previously for boolean functions of two variables. The rows are grouped to reflect natural similarity classes among the propositions. In a future discussion, these classes will be given additional explanation and motivation as the orbits of a certain transformation group acting on the set of 16 propositions. Notice that four of the propositions, in their logical expressions, resemble those given in the table for X^. Thus the first set of propositions {fi} is automatically embedded in the present set {gj}, and the corresponding inclusions are indicated at the far left margin of the table.
Tacit Extensions
I would really like to have slipped imperceptibly into this lecture, as into all the others I shall be delivering, perhaps over the years ahead.
Michel Foucault, The Discourse on Language, [Fou, 215]
Strictly speaking, however, there is a subtle distinction in type between the function fi : X → B and the corresponding function gj : EX → B, even though they share the same logical expression. Being human, we insist on preserving all the aesthetic delights afforded by the abstractly unified form of the "cake" while giving up none of the diverse contents that its substantive consummation can provide. In short, we want to maintain the logical equivalence of expressions that represent the same proposition, while appreciating the full diversity of that proposition's functional and typical representatives. Both perspectives, and all the levels of abstraction extending through them, have their reasons, as will develop in time.
Because this special circumstance points up an important general theme, it is a good idea to discuss it more carefully. Whenever there arises a situation like this, where one alphabet X is a subset of another alphabet Y, then we say that any proposition f : 〈X〉 → B has a tacit extension to a proposition \(\epsilon\)f : 〈Y〉 → B, and that the space (〈X〉 → B) has an automatic embedding within the space (〈Y〉 → B). The extension is defined in such a way that \(\epsilon\)f puts the same constraint on the variables of X that are contained in Y as the proposition f initially did, while it puts no constraint on the variables of Y outside of X, in effect, conjoining the two constraints.
If the variables in question are indexed as X = {x1, …, xn} and Y = {x1, …, xn, …, xn+k}, then the definition of the tacit extension from X to Y may be expressed in the form of an equation:
\[\epsilon\]f(x1, …, xn, …, xn+k) = f(x1, …, xn).
On formal occasions, such as the present context of definition, the tacit extension from X to Y is explicitly symbolized by the operator \(\epsilon\) : (〈X〉 → B) → (〈Y〉 → B), where the appropriate alphabets X and Y are understood from context, but normally one may leave the "\(\epsilon\)" silent.
Let's explore what this means for the present Example. Here, X = {A} and Y = EX = {A, dA}. For each of the propositions fi over X, specifically, those whose expression ei lies in the collection {0, (A), A, 1}, the tacit extension \(\epsilon\)f of f to EX can be phrased as a logical conjunction of two factors, fi = ei · \(\tau\) , where \(\tau\) is a logical tautology that uses all the variables of Y – X. Working in these terms, the tacit extensions \(\epsilon\)f of f to EX may be explicated as shown in Table 15.
|
In its effect on the singular propositions over X, this analysis has an interesting interpretation. The tacit extension takes us from thinking about a particular state, like A or (A), to considering the collection of outcomes, the outgoing changes or the singular dispositions, that spring from that state.
Example 2. Drives and Their Vicissitudes
I open my scuttle at night and see the far-sprinkled systems,
And all I see, multiplied as high as I can cipher, edge but
the rim of the farther systems.Walt Whitman, Leaves of Grass, [Whi, 81]
Before we leave the one-feature case let's look at a more substantial example, one that illustrates a general class of curves that can be charted through the extended feature spaces and that provides an opportunity to discuss a number of important themes concerning their structure and dynamics.
Again, let X = {x1} = {A}. In the discussion that follows I will consider a class of trajectories having the property that dkA = 0 for all k greater than some fixed m, and I indulge in the use of some picturesque terms that describe salient classes of such curves. Given the finite order condition, there is a highest order non-zero difference dmA exhibited at each point in the course of any determinate trajectory that one may wish to consider. With respect to any point of the corresponding orbit or curve let us call this highest order differential feature dmA the drive at that point. Curves of constant drive dmA are then referred to as "mth gear curves".
- Scholium. The fact that a difference calculus can be developed for boolean functions is well known [Fuji], [Koh, § 8-4] and was probably familiar to Boole, who was an expert in difference equations before he turned to logic. And of course there is the strange but true story of how the Turin machines of the 1840's prefigured the Turing machines of the 1940's [Men, 225-297]. At the very outset of general purpose, mechanized computing we find that the motive power driving the Analytical Engine of Babbage, the kernel of an idea behind all of his wheels, was exactly his notion that difference operations, suitably trained, can serve as universal joints for any conceivable computation [M&M], [Mel, ch. 4].
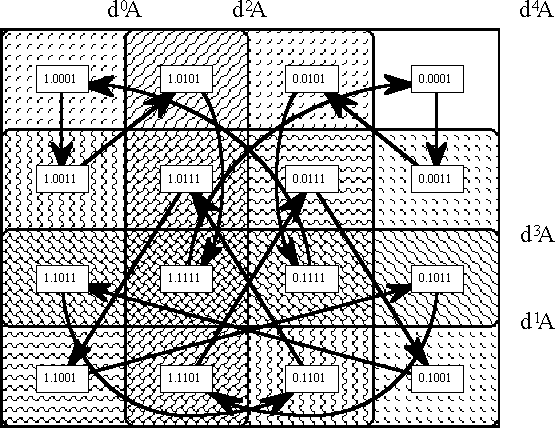
Given this language, the particular Example that I take up here can be described as the family of 4th gear curves through E4X = 〈A, dA, d2A, d3A, d4A〉. These are the trajectories generated subject to the dynamic law d4A = 1, where it is understood in such a statement that all higher order differences are equal to 0. Since d4A and all higher dkA are fixed, the temporal or transitional conditions (initial, mediate, terminal - transient or stable states) vary only with respect to their projections as points of E3X = 〈A, dA, d2A, d3A〉. Thus, there is just enough space in a planar venn diagram to plot all of these orbits and to show how they partition the points of E3X. It turns out that there are exactly two possible orbits, of eight points each, as illustrated in Figure 16.
With a little thought it is possible to devise an indexing scheme for the general run of dynamic states that allows for comparing universes of discourse that weigh in on different scales of observation. With this end in sight, let us index the states q in EmX with the dyadic rationals (or the binary fractions) in the half-open interval [0, 2). Formally and canonically, a state qr is indexed by a fraction r = s/t whose denominator is the power of two t = 2m and whose numerator is a binary numeral that is formed from the coefficients of state in a manner to be described next. The differential coefficients of the state q are just the values dkA(q), for k = 0 to m, where d0A is defined as being identical to A. To form the binary index d0.d1…dm of the state q the coefficient dkA(q) is read off as the binary digit dk associated with the place value 2–k. Expressed by way of algebraic formulas, the rational index r of the state q can be given by the following equivalent formulations:
|
Applied to the example of fourth gear curves, this scheme results in the data of Tables 17-a and 17-b, which exhibit one period for each orbit. The states in each orbit are listed as ordered pairs ‹pi, qj›, where pi may be read as a temporal parameter that indicates the present time of the state, and where j is the decimal equivalent of the binary numeral s. Informally and more casually, the Tables exhibit the states qs as subscripted with the numerators of their rational indices, taking for granted the constant denominators of 2m = 24 = 16. Within this set-up, the temporal successions of states can be reckoned as given by a kind of parallel round-up rule. That is, if ‹dk, dk+1› is any pair of adjacent digits in the state index r, then the value of dk in the next state is dk′ = dk + dk+1.
| Time | State | A | dA | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| pi | qj | d0A | d1A | d2A | d3A | d4A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Time | State | A | dA | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| pi | qj | d0A | d1A | d2A | d3A | d4A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Work Area
|
|
Table 2 exhibits the scheme of notation I use to formalize the domain of propositional calculus, corresponding to the logical content of truth tables and venn diagrams. Although it overworks the square brackets a bit, I also use either one of the equivalent notations [n] or n to denote the data type of a finite set on n elements.
| Symbol | Notation | Description | Type |
|---|---|---|---|
| \(\mathcal{A}\) | \(\{ a_1, \ldots, a_n \}\) | Alphabet | \([n] = \mathbf{n}\) |
| \(A_i\!\) | \(\{ (a_i), a_i \}\!\) | Dimension \(i\!\) | \(\mathbb{B}\) |
| \(A\!\) |
\(\langle \mathcal{A} \rangle\) |
Set of cells, |
\(\mathbb{B}^n\) |
| \(A^*\!\) | \((\operatorname{hom} : A \to \mathbb{B})\) | Linear functions | \((\mathbb{B}^n)^* \cong \mathbb{B}^n\) |
| \(A\!\uparrow\) | \((A \to \mathbb{B})\) | Boolean functions | \(\mathbb{B}^n \to \mathbb{B}\) |
| \(A^\circ\) |
\([ \mathcal{A} ]\) |
Universe of discourse |
\((\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B}))\) |