Difference between revisions of "Directory:Jon Awbrey/Papers/Differential Propositional Calculus"

MyWikiBiz, Author Your Legacy — Saturday November 23, 2024
Jump to navigationJump to search
(add content by Jon Awbrey)
(revert to automatic section numbering)
 
(268 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
{{DISPLAYTITLE:Differential Propositional Calculus}}
 
{{DISPLAYTITLE:Differential Propositional Calculus}}
 +
'''Author: [[User:Jon Awbrey|Jon Awbrey]]'''
  
−
==Differential Logic : Series A==
+
A '''differential propositional calculus''' is a [[propositional calculus]] extended by a set of terms for describing aspects of change and difference, for example, processes that take place in a [[universe of discourse]] or transformations that map a source universe into a target universe.
  
−
===Note 1===
+
==Casual Introduction==
  
−
One of the first things that you can do, once you have a really decent calculus for boolean functions or propositional logic, whatever you want to call it, is to compute the differentials of these functions or propositions.
+
Consider the situation represented by the venn diagram in Figure 1.
  
−
Now there are many ways to dance around this idea, and I feel like I have tried them all, before one gets down to acting on it, and there many issues of interpretation and justification that we will have to clear up after the fact, that is, before we can be sure that it all really makes any sense, but I think this time I'll just jump in, and show you the form in which this idea first came to me.
+
{| align="center" border="0" cellspacing="10" style="text-align:center; width:100%"
 +
| [[Image:DiffPropCalc1.jpg|500px]]
 +
|-
 +
| height="20px" valign="top" | <math>\text{Figure 1.} ~~ \text{Local Habitations, And Names}\!</math>
 +
|}
  
−
Start with a proposition of the form ''x'' & ''y'', which I graph as two labels attached to a root node, so:
+
The area of the rectangle represents a universe of discourse, <math>X.\!</math>  This might be a population of individuals having various additional properties or it might be a collection of locations that various individuals occupy.  The area of the &ldquo;circle&rdquo; represents the individuals that have the property <math>q\!</math> or the locations that fall within the corresponding region <math>Q.\!</math>  Four individuals, <math>a, b, c, d,\!</math> are singled out by name.  It happens that <math>b\!</math> and <math>c\!</math> currently reside in region <math>Q\!</math> while <math>a\!</math> and <math>d\!</math> do not.
  
−
<pre>
+
Now consider the situation represented by the venn diagram in Figure&nbsp;2.
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                      x y                      |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|                    x and y                    |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
Written as a string, this is just the concatenation ''x y''.
+
{| align="center" border="0" cellspacing="10" style="text-align:center; width:100%"
 +
| [[Image:DiffPropCalc2.jpg|500px]]
 +
|-
 +
| height="20px" valign="top" | <math>\text{Figure 2.} ~~ \text{Same Names, Different Habitations}\!</math>
 +
|}
  
−
The proposition ''xy'' may be taken as a boolean function ''f''(''x'',&nbsp;''y'') having the abstract type ''f''&nbsp;:&nbsp;'''B'''&nbsp;&times;&nbsp;'''B'''&nbsp;&rarr;&nbsp;'''B''', where '''B''' = {0,&nbsp;1} is read in such a way that 0 means ''false'' and 1 means ''true''.
+
Figure 2 differs from Figure 1 solely in the circumstance that the object <math>c\!</math> is outside the region <math>Q\!</math> while the object <math>d\!</math> is inside the region <math>Q.\!</math>  So far, there is nothing that says that our encountering these Figures in this order is other than purely accidental, but if we interpret the present sequence of frames as a &ldquo;moving picture&rdquo; representation of their natural order in a temporal process, then it would be natural to say that <math>a\!</math> and <math>b\!</math> have remained as they were with regard to quality <math>q\!</math> while <math>c\!</math> and <math>d\!</math> have changed their standings in that respect.  In particular, <math>c\!</math> has moved from the region where <math>q\!</math> is <math>\mathrm{true}\!</math> to the region where <math>q\!</math> is <math>\mathrm{false}\!</math> while <math>d\!</math> has moved from the region where <math>q\!</math> is <math>\mathrm{false}\!</math> to the region where <math>q\!</math> is <math>\mathrm{true}.\!</math>
  
−
In this style of graphical representation, the value ''true'' looks like a blank label and the value ''false'' looks like an edge.
+
Figure&nbsp;3 reprises the situation shown in Figure&nbsp;1, but this time interpolates a new quality that is specifically tailored to account for the relation between Figure&nbsp;1 and Figure&nbsp;2.
  
−
<pre>
+
{| align="center" border="0" cellspacing="10" style="text-align:center; width:100%"
−
o-------------------------------------------------o
+
| [[Image:DiffPropCalc3.jpg|500px]]
−
|                                                 |
+
|-
−
|                                                 |
+
| height="20px" valign="top" | <math>\text{Figure 3.} ~~ \text{Back, To The Future}\!</math>
−
|                        @                        |
+
|}
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|                     true                      |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
<pre>
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                        o                        |
 
−
|                        |                        |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|                     false                      |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
Back to the proposition ''xy''.  Imagine yourself standing in a fixed cell of the corresponding venn diagram, say, the cell where the proposition ''xy'' is true, as pictured:
+
This new quality, <math>\mathrm{d}q,\!</math> is an example of a ''differential quality'', since its absence or presence qualifies the absence or presence of change occurring in another quality.  As with any other quality, it is represented in the venn diagram by means of a &ldquo;circle&rdquo; that distinguishes two halves of the universe of discourse, in this case, the portions of <math>X\!</math> outside and inside the region <math>\mathrm{d}Q.\!</math>
  
−
<pre>
+
Figure 1 represents a universe of discourse, <math>X,\!</math> together with a basis of discussion, <math>\{ q \},\!</math> for expressing propositions about the contents of that universe.  Once the quality <math>q\!</math> is given a name, say, the symbol <math>{}^{\backprime\backprime} q {}^{\prime\prime},\!</math> we have the basis for a formal language that is specifically cut out for discussing <math>X\!</math> in terms of <math>q,\!</math> and this formal language is more formally known as the ''propositional calculus'' with alphabet <math>\{ {}^{\backprime\backprime} q {}^{\prime\prime} \}.\!</math>
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                                                |
 
−
|          o-----------o  o-----------o          |
 
−
|        /             \ /            \         |
 
−
|        /               o              \       |
 
−
|      /               /%\               \       |
 
−
|      /              /%%%\               \     |
 
−
|    o              o%%%%%o              o    |
 
−
|    |              |%%%%%|              |    |
 
−
|    |              |%%%%%|              |    |
 
−
|    |      x      |%%%%%|      y      |    |
 
−
|    |              |%%%%%|              |    |
 
−
|    |              |%%%%%|              |    |
 
−
|    o              o%%%%%o              o    |
 
−
|      \               \%%%/               /     |
 
−
|      \               \%/              /      |
 
−
|        \               o              /        |
 
−
|        \             / \             /        |
 
−
|          o-----------o  o-----------o          |
 
−
|                                                |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
Now ask yourself:  What is the value of the proposition ''xy'' at a distance of ''dx'' and ''dy'' from the cell ''xy'' where you are standing?
+
In the context marked by <math>X\!</math> and <math>\{ q \}\!</math> there are but four different pieces of information that can be expressed in the corresponding propositional calculus, namely, the propositions:  <math>\mathrm{false}, ~ \lnot q, ~ q, ~ \mathrm{true}.\!</math>  Referring to the sample of points in Figure&nbsp;1, the constant proposition <math>\mathrm{false}\!</math> holds of no points, the proposition <math>\lnot q\!</math> holds of <math>a\!</math> and <math>d,\!</math> the proposition <math>q\!</math> holds of <math>b\!</math> and <math>c,\!</math> and the constant proposition <math>\mathrm{true}\!</math> holds of all points in the sample.
  
−
Don't think about it -- just compute:
+
Figure&nbsp;3 preserves the same universe of discourse and extends the basis of discussion to a set of two qualities, <math>\{ q, \mathrm{d}q \}.\!</math>  In parallel fashion, the initial propositional calculus is extended by means of the enlarged alphabet, <math>\{ {}^{\backprime\backprime} q {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{d}q {}^{\prime\prime} \}.\!</math>  Any propositional calculus over two basic propositions allows for the expression of 16 propositions all together.  Just by way of salient examples in the present setting, we can pick out the most informative propositions that apply to each of our sample points.  Using overlines to express logical negation, these are given as follows:
  
−
<pre>
+
:* <p><math>\overline{q} ~ \overline{\mathrm{d}q}\!</math> describes <math>a\!</math></p>
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                  dx o  o dy                  |
 
−
|                    / \ / \                    |
 
−
|                  x o---@---o y                  |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|              (x + dx) and (y + dy)              |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
To make future graphs easier to draw in Ascii land, I will use devices like <code>@=@=@</code> and <code>o=o=o</code> to identify several nodes into one, as in this next redrawing:
+
:* <p><math>\overline{q} ~ \mathrm{d}q\!</math> describes <math>d\!</math></p>
  
−
<pre>
+
:* <p><math>q ~ \overline{\mathrm{d}q}\!</math> describes <math>b\!</math></p>
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                  x  dx y  dy                  |
 
−
|                  o---o o---o                  |
 
−
|                    \ | |  /                    |
 
−
|                    \ | | /                     |
 
−
|                      \| |/                     |
 
−
|                      @=@                      |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|              (x + dx) and (y + dy)              |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
However you draw it, these expressions follow because the expression ''x'' + ''dx'', where the plus sign indicates (mod 2) addition in '''B''', and thus corresponds to an exclusive-or in logic, parses to a graph of the following form:
+
:* <p><math>q ~ \mathrm{d}q\!</math> describes <math>c\!</math></p>
  
−
<pre>
+
Table&nbsp;4 exhibits the rules of inference that give the differential quality <math>\mathrm{d}q\!</math> its meaning in practice.
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                    x    dx                    |
 
−
|                      o---o                      |
 
−
|                      \ /                      |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|                      x + dx                    |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
Next question:  What is the difference between the value of the proposition ''xy'' "over there" and the value of the proposition ''xy'' where you are, all expressed as general formula, of course?  Here 'tis:
+
<br>
  
−
<pre>
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:center; width:60%"
−
o-------------------------------------------------o
+
|+ style="height:30px" | <math>\text{Table 4.} ~~ \text{Differential Inference Rules}\!</math>
−
|                                                 |
+
|
−
|            x  dx y  dy                        |
+
<math>\begin{matrix}
−
|            o---o o---o                        |
+
\text{From} & \overline{q}
−
|              \ | |  /                          |
+
& \text{and} & \overline{\mathrm{d}q}
−
|              \ | | /                          |
+
& \text{infer} & \overline{q} & \text{next.}
−
|                \| |/        x y                |
+
\\[8pt]
−
|                o=o-----------o                |
+
\text{From} & \overline{q}
−
|                  \           /                  |
+
& \text{and} & \mathrm{d}q
−
|                  \         /                  |
+
& \text{infer} & q & \text{next.}
−
|                    \       /                    |
+
\\[8pt]
−
|                    \     /                    |
+
\text{From} & q
−
|                      \   /                      |
+
& \text{and} & \overline{\mathrm{d}q}
−
|                      \ /                      |
+
& \text{infer} & q & \text{next.}
−
|                        @                        |
+
\\[8pt]
−
|                                                |
+
\text{From} & q
−
o-------------------------------------------------o
+
& \text{and} & \mathrm{d}q
−
|          ((x + dx) & (y + dy)) - xy            |
+
& \text{infer} & \overline{q} & \text{next.}
−
o-------------------------------------------------o
+
\end{matrix}</math>
−
</pre>
+
|}
  
−
Oh, I forgot to mention:  Computed over '''B''', plus and minus are the very same operation.  This will make the relationship between the differential and the integral parts of the resulting calculus slightly stranger than usual, but never mind that now.
+
<br>
  
−
Last question, for now:  What is the value of this expression from your current standpoint, that is, evaluated at the point where ''xy'' is true?  Well, substituting 1 for ''x'' and 1 for ''y'' in the graph amounts to the same thing as erasing those labels:
+
==Cactus Calculus==
  
−
<pre>
+
Table 5 outlines a syntax for propositional calculus based on two types of logical connectives, both of variable <math>k\!</math>-ary scope.
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|            dx    dy                            |
 
−
|            o---o o---o                        |
 
−
|              \  | |  /                          |
 
−
|              \ | | /                          |
 
−
|                \| |/                            |
 
−
|                o=o-----------o                |
 
−
|                  \          /                  |
 
−
|                  \        /                  |
 
−
|                    \      /                    |
 
−
|                    \    /                    |
 
−
|                      \   /                      |
 
−
|                      \ /                      |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|          ((1 + dx) & (1 + dy)) - 1&1          |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
And this is equivalent to the following graph:
+
* A bracketed list of propositional expressions in the form <math>\texttt{(} e_1, e_2, \ldots, e_{k-1}, e_k \texttt{)}\!</math> indicates that exactly one of the propositions <math>e_1, e_2, \ldots, e_{k-1}, e_k\!</math> is false.
  
−
<pre>
+
* A concatenation of propositional expressions in the form <math>e_1 ~ e_2 ~ \ldots ~ e_{k-1} ~ e_k\!</math> indicates that all of the propositions <math>e_1, e_2, \ldots, e_{k-1}, e_k\!</math> are true, in other words, that their [[logical conjunction]] is true.
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                    dx  dy                    |
 
−
|                      o  o                      |
 
−
|                      \ /                       |
 
−
|                        o                        |
 
−
|                        |                        |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|                    dx or dy                    |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
Enough for the moment.  Explanation to follow.
+
<br>
  
−
===Note 2===
+
{| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:75%"
 +
|+ style="height:30px" | <math>\text{Table 5.} ~~ \text{Syntax and Semantics of a Calculus for Propositional Logic}\!</math>
 +
|- style="height:40px; background:ghostwhite"
 +
| <math>\text{Expression}~\!</math>
 +
| <math>\text{Interpretation}\!</math>
 +
| <math>\text{Other Notations}\!</math>
 +
|-
 +
| &nbsp;
 +
| <math>\text{True}\!</math>
 +
| <math>1\!</math>
 +
|-
 +
| <math>\texttt{(~)}\!</math>
 +
| <math>\text{False}\!</math>
 +
| <math>0\!</math>
 +
|-
 +
| <math>x\!</math>
 +
| <math>x\!</math>
 +
| <math>x\!</math>
 +
|-
 +
| <math>\texttt{(} x \texttt{)}\!</math>
 +
| <math>\text{Not}~ x\!</math>
 +
|
 +
<math>\begin{matrix}
 +
x'
 +
\\
 +
\tilde{x}
 +
\\
 +
\lnot x
 +
\end{matrix}\!</math>
 +
|-
 +
| <math>x~y~z\!</math>
 +
| <math>x ~\text{and}~ y ~\text{and}~ z\!</math>
 +
| <math>x \land y \land z\!</math>
 +
|-
 +
| <math>\texttt{((} x \texttt{)(} y \texttt{)(} z \texttt{))}\!</math>
 +
| <math>x ~\text{or}~ y ~\text{or}~ z\!</math>
 +
| <math>x \lor y \lor z\!</math>
 +
|-
 +
| <math>\texttt{(} x ~ \texttt{(} y \texttt{))}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
x ~\text{implies}~ y
 +
\\
 +
\mathrm{If}~ x ~\text{then}~ y
 +
\end{matrix}</math>
 +
| <math>x \Rightarrow y\!</math>
 +
|-
 +
| <math>\texttt{(} x \texttt{,} y \texttt{)}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
x ~\text{not equal to}~ y
 +
\\
 +
x ~\text{exclusive or}~ y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
x \ne y
 +
\\
 +
x + y
 +
\end{matrix}</math>
 +
|-
 +
| <math>\texttt{((} x \texttt{,} y \texttt{))}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
x ~\text{is equal to}~ y
 +
\\
 +
x ~\text{if and only if}~ y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
x = y
 +
\\
 +
x \Leftrightarrow y
 +
\end{matrix}</math>
 +
|-
 +
| <math>\texttt{(} x \texttt{,} y \texttt{,} z \texttt{)}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{Just one of}
 +
\\
 +
x, y, z
 +
\\
 +
\text{is false}.
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
x'y~z~ & \lor
 +
\\
 +
x~y'z~ & \lor
 +
\\
 +
x~y~z' &
 +
\end{matrix}</math>
 +
|-
 +
| <math>\texttt{((} x \texttt{),(} y \texttt{),(} z \texttt{))}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{Just one of}
 +
\\
 +
x, y, z
 +
\\
 +
\text{is true}.
 +
\\
 +
&
 +
\\
 +
\text{Partition all}
 +
\\
 +
\text{into}~ x, y, z.
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
x~y'z' & \lor
 +
\\
 +
x'y~z' & \lor
 +
\\
 +
x'y'z~ &
 +
\end{matrix}</math>
 +
|-
 +
|
 +
<math>\begin{matrix}
 +
\texttt{((} x \texttt{,} y \texttt{),} z \texttt{)}
 +
\\
 +
&
 +
\\
 +
\texttt{(} x \texttt{,(} y \texttt{,} z \texttt{))}
 +
\end{matrix}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{Oddly many of}
 +
\\
 +
x, y, z
 +
\\
 +
\text{are true}.
 +
\end{matrix}\!</math>
 +
|
 +
<p><math>x + y + z\!</math></p>
 +
<br>
 +
<p><math>\begin{matrix}
 +
x~y~z~ & \lor
 +
\\
 +
x~y'z' & \lor
 +
\\
 +
x'y~z' & \lor
 +
\\
 +
x'y'z~ &
 +
\end{matrix}\!</math></p>
 +
|-
 +
| <math>\texttt{(} w \texttt{,(} x \texttt{),(} y \texttt{),(} z \texttt{))}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{Partition}~ w
 +
\\
 +
\text{into}~ x, y, z.
 +
\\
 +
&
 +
\\
 +
\text{Genus}~ w ~\text{comprises}
 +
\\
 +
\text{species}~ x, y, z.
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
w'x'y'z' & \lor
 +
\\
 +
w~x~y'z' & \lor
 +
\\
 +
w~x'y~z' & \lor
 +
\\
 +
w~x'y'z~ &
 +
\end{matrix}</math>
 +
|}
  
−
We have just met with the fact that the differential of the "and" is the "or" of the differentials.
+
<br>
  
−
: ''x'' and ''y'' --Diff--> ''dx'' or ''dy''.
+
All other propositional connectives can be obtained through combinations of these two forms. Strictly speaking, the concatenation form is dispensable in light of the bracket form, but it is convenient to maintain it as an abbreviation for more complicated bracket expressions.  While working with expressions solely in propositional calculus, it is easiest to use plain parentheses for logical connectives.  In contexts where parentheses are needed for other purposes &ldquo;teletype&rdquo; parentheses <math>\texttt{(} \ldots \texttt{)}\!</math> or barred parentheses <math>(\!| \ldots |\!)</math> may be used for logical operators.
  
−
<pre>
+
The briefest expression for logical truth is the empty word, abstractly denoted <math>\boldsymbol\varepsilon\!</math> or <math>\boldsymbol\lambda\!</math> in formal languages, where it forms the identity element for concatenation.  It may be given visible expression in this context by means of the logically equivalent form <math>\texttt{((~))},\!</math> or, especially if operating in an algebraic context, by a simple <math>1.\!</math>  Also when working in an algebraic mode, the plus sign <math>{+}\!</math> may be used for [[exclusive disjunction]].  For example, we have the following paraphrases of algebraic expressions:
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                                    dx  dy      |
 
−
|                                    o  o      |
 
−
|                                      \ /       |
 
−
|                                      o        |
 
−
|        x y                            |        |
 
−
|        @          --Diff-->         @        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|        x y        --Diff-->     ((dx) (dy))   |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
It will be necessary to develop a more refined analysis of this statement directly, but that is roughly the nub of it.
+
{| align="center" cellpadding="6" style="text-align:center"
 +
|
 +
<math>\begin{matrix}
 +
x + y ~=~ \texttt{(} x, y \texttt{)}
 +
\\[6pt]
 +
x + y + z ~=~ \texttt{((} x, y \texttt{)}, z \texttt{)} ~=~ \texttt{(} x, \texttt{(} y, z \texttt{))}
 +
\end{matrix}</math>
 +
|}
  
−
If the form of the above statement reminds you of De&nbsp;Morgan's rule, it is no accident, as differentiation and negation turn out to be closely related operations.  Indeed, one can find discussions of logical difference calculus in the Boole-De&nbsp;Morgan correspondence and [[C.S. Peirce]] also made use of differential operators in a logical context, but the exploration of these ideas has been hampered by a number of factors, not the least of which being a syntax adequate to handle the complexity of expressions that evolve.
+
It is important to note that the last expressions are not equivalent to the triple bracket <math>\texttt{(} x, y, z \texttt{)}.\!</math>
  
−
For my part, it was definitely a case of the calculus being smarter than the calculator thereof.  The graphical pictures were catalytic in their power over my thinking process, leading me so quickly past so many obstructions that I did not have time to think about all of the difficulties that would otherwise have inhibited the derivation.  It did eventually became necessary to write all this up in a linear script, and to deal with the various problems of interpretation and justification that I could imagine, but that took another 120 pages, and so, if you don't like this intuitive approach, then let that be your sufficient notice.
+
For more information about this syntax for propositional calculus, see the entries on [[minimal negation operator]]s, [[zeroth order logic]], and [[Differential Propositional Calculus#Table A1. Propositional Forms on Two Variables|Table A1 in Appendix 1]].
  
−
Let us run through the initial example again, this time attempting to interpret the formulas that develop at each stage along the way.
+
==Formal Development==
  
−
We begin with a proposition or a boolean function ''f''(''x'',&nbsp;''y'') = ''xy''.
+
The preceding discussion outlined the ideas leading to the differential extension of propositional logic.  The next task is to lay out the concepts and terminology that are needed to describe various orders of differential propositional calculi.
  
−
<pre>
+
===Elementary Notions===
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                                                |
 
−
|          o-----------o  o-----------o          |
 
−
|        /            \ /            \        |
 
−
|        /              o              \        |
 
−
|      /              /`\              \      |
 
−
|      /              /```\              \      |
 
−
|    o              o`````o              o    |
 
−
|    |              |`````|              |    |
 
−
|    |              |`````|              |    |
 
−
|    |      x      |``f``|      y      |    |
 
−
|    |              |`````|              |    |
 
−
|    |              |`````|              |    |
 
−
|    o              o`````o              o    |
 
−
|      \              \```/              /      |
 
−
|      \              \`/              /      |
 
−
|        \              o              /        |
 
−
|        \            / \            /        |
 
−
|          o-----------o  o-----------o          |
 
−
|                                                |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                      x y                      |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| f =                   x y                      |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
A function like this has an abstract type and a concrete type.  The abstract type is what we invoke when we write things like ''f''&nbsp;:&nbsp;'''B'''&nbsp;&times;&nbsp;'''B'''&nbsp;&rarr;&nbsp;'''B''' or ''f''&nbsp;:&nbsp;'''B'''<sup>2</sup>&nbsp;&rarr;&nbsp;'''B'''. The concrete type takes into account the qualitative dimensions or the "units" of the case, which can be explained as follows.
+
Logical description of a universe of discourse begins with a set of logical signs.  For the sake of simplicity in a first approach, assume that these logical signs are collected in the form of a finite alphabet, <math>\mathfrak{A} = \{ {}^{\backprime\backprime} a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} a_n {}^{\prime\prime} \}.\!</math>  Each of these signs is interpreted as denoting a logical feature, for instance, a property that objects in the universe of discourse may have or a proposition about objects in the universe of discourse.  Corresponding to the alphabet <math>\mathfrak{A}\!</math> there is then a set of logical features, <math>\mathcal{A} = \{ a_1, \ldots, a_n \}.\!</math>
  
−
* Let ''X'' be the set of values {(''x''), ''x''} = {not ''x'', ''x''}.
+
A set of logical features, <math>\mathcal{A} = \{ a_1, \ldots, a_n \},\!</math> affords a basis for generating an <math>n\!</math>-dimensional universe of discourse, written <math>A^\bullet = [ \mathcal{A} ] = [ a_1, \ldots, a_n ].\!</math>  It is useful to consider a universe of discourse as a categorical object that incorporates both the set of points <math>A = \langle a_1, \ldots, a_n \rangle\!</math> and the set of propositions <math>A^\uparrow = \{ f : A \to \mathbb{B} \}\!</math> that are implicit with the ordinary picture of a venn diagram on <math>n\!</math> features.  Accordingly, the universe of discourse <math>A^\bullet\!</math> may be regarded as an ordered pair <math>(A, A^\uparrow)\!</math> having the type <math>(\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B})),\!</math> and this last type designation may be abbreviated as <math>\mathbb{B}^n\ +\!\to \mathbb{B},\!</math> or even more succinctly as <math>[ \mathbb{B}^n ].\!</math>  For convenience, the data type of a finite set on <math>n\!</math> elements may be indicated by either one of the equivalent notations, <math>[n]\!</math> or <math>\mathbf{n}.\!</math>
  
−
* Let ''Y'' be the set of values {(''y''), ''y''} = {not ''y'', ''y''}.
+
Table&nbsp;6 summarizes the notations that are needed to describe ordinary propositional calculi in a systematic fashion.
  
−
Then interpret the usual propositions about ''x'', ''y'' as functions of the concrete type ''f''&nbsp;:&nbsp;''X''&nbsp;&times;&nbsp;''Y''&nbsp;&rarr;&nbsp;'''B'''.
+
<br>
  
−
We are going to consider various "operators" on these functions.  Here, an operator ''F'' is a function that takes one function ''f'' into another function ''Ff''.
+
{| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:75%"
 +
|+ style="height:30px" | <math>\text{Table 6.} ~~ \text{Propositional Calculus : Basic Notation}\!</math>
 +
|- style="height:40px; background:ghostwhite"
 +
| <math>\text{Symbol}\!</math>
 +
| <math>\text{Notation}\!</math>
 +
| <math>\text{Description}\!</math>
 +
| <math>\text{Type}\!</math>
 +
|-
 +
| <math>\mathfrak{A}\!</math>
 +
| <math>\{ {}^{\backprime\backprime} a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} a_n {}^{\prime\prime} \}\!</math>
 +
| <math>\text{Alphabet}\!</math>
 +
| <math>[n] = \mathbf{n}\!</math>
 +
|-
 +
| <math>\mathcal{A}\!</math>
 +
| <math>\{ a_1, \ldots, a_n \}\!</math>
 +
| <math>\text{Basis}\!</math>
 +
| <math>[n] = \mathbf{n}\!</math>
 +
|-
 +
| <math>A_i\!</math>
 +
| <math>\{ \texttt{(} a_i \texttt{)}, a_i \}\!</math>
 +
| <math>\text{Dimension}~ i\!</math>
 +
| <math>\mathbb{B}\!</math>
 +
|-
 +
| <math>A\!</math>
 +
|
 +
<math>\begin{matrix}
 +
\langle \mathcal{A} \rangle
 +
\\[2pt]
 +
\langle a_1, \ldots, a_n \rangle
 +
\\[2pt]
 +
\{ (a_1, \ldots, a_n) \}
 +
\\[2pt]
 +
A_1 \times \ldots \times A_n
 +
\\[2pt]
 +
\textstyle \prod_{i=1}^n A_i
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{Set of cells},
 +
\\[2pt]
 +
\text{coordinate tuples},
 +
\\[2pt]
 +
\text{points, or vectors}
 +
\\[2pt]
 +
\text{in the universe}
 +
\\[2pt]
 +
\text{of discourse}
 +
\end{matrix}</math>
 +
| <math>\mathbb{B}^n\!</math>
 +
|-
 +
| <math>A^*\!</math>
 +
| <math>(\mathrm{hom} : A \to \mathbb{B})\!</math>
 +
| <math>\text{Linear functions}\!</math>
 +
| <math>(\mathbb{B}^n)^* \cong \mathbb{B}^n\!</math>
 +
|-
 +
| <math>A^\uparrow\!</math>
 +
| <math>(A \to \mathbb{B})\!</math>
 +
| <math>\text{Boolean functions}\!</math>
 +
| <math>\mathbb{B}^n \to \mathbb{B}\!</math>
 +
|-
 +
| <math>A^\bullet\!</math>
 +
|
 +
<math>\begin{matrix}
 +
[\mathcal{A}]
 +
\\[2pt]
 +
(A, A^\uparrow)
 +
\\[2pt]
 +
(A ~+\!\to \mathbb{B})
 +
\\[2pt]
 +
(A, (A \to \mathbb{B}))
 +
\\[2pt]
 +
[a_1, \ldots, a_n]
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{Universe of discourse}
 +
\\[2pt]
 +
\text{based on the features}
 +
\\[2pt]
 +
\{ a_1, \ldots, a_n \}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
(\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B}))
 +
\\[2pt]
 +
(\mathbb{B}^n ~+\!\to \mathbb{B})
 +
\\[2pt]
 +
[\mathbb{B}^n]
 +
\end{matrix}</math>
 +
|}
  
−
The first couple of operators that we need to consider are logical analogues of those that occur in the classical "finite difference calculus", namely:
+
<br>
  
−
* The ''difference'' operator &Delta;, written here as ''D''.
+
===Special Classes of Propositions===
  
−
* The ''enlargement'' operator &Epsilon;, written here as ''E''.
+
A ''basic proposition'', ''coordinate proposition'', or ''simple proposition'' in the universe of discourse <math>[a_1, \ldots, a_n]</math> is one of the propositions in the set <math>\{ a_1, \ldots, a_n \}.</math>
  
−
These days, ''E'' is more often called the ''shift'' operator.
+
Among the <math>2^{2^n}</math> propositions in <math>[a_1, \ldots, a_n]</math> are several families of <math>2^n\!</math> propositions each that take on special forms with respect to the basis <math>\{ a_1, \ldots, a_n \}.</math>  Three of these families are especially prominent in the present context, the ''linear'', the ''positive'', and the ''singular'' propositions.  Each family is naturally parameterized by the coordinate <math>n\!</math>-tuples in <math>\mathbb{B}^n</math> and falls into <math>n + 1\!</math> ranks, with a binomial coefficient <math>\tbinom{n}{k}</math> giving the number of propositions that have rank or weight <math>k.\!</math>
  
−
In order to describe the universe in which these operators operate, it will be necessary to enlarge our original universe of discourse.  We mount up from the space ''U'' = ''X''&nbsp; &times;&nbsp;''Y'' to its ''differential extension'',
+
<ul>
−
''EU'' = ''U''&nbsp; &times;&nbsp;''dU'' = ''X''&nbsp;&times;&nbsp;''Y''&nbsp;&times;&nbsp;''dX''&nbsp; &times;&nbsp;''dY'', with ''dX'' = {(''dx''), ''dx''} and ''dY'' = {(''dy''), ''dy''}.  The interpretations of these new symbols can be diverse, but the easiest for now is just to say that ''dx'' means "change x" and ''dy'' means "change y".  To draw the differential extension ''EU'' of our present universe ''U'' = ''X''&nbsp; &times;&nbsp;''Y'' as a venn diagram, it would take us four logical dimensions ''X'', ''Y'', ''dX'', ''dY'', but we can project a suggestion of what it's about on the universe ''X''&nbsp; &times;&nbsp;''Y'' by drawing arrows that cross designated borders, labeling the arrows as ''dx'' when crossing the border between ''x'' and (''x'') and as ''dy'' when crossing the border between ''y'' and (''y''), in either direction, in either case.
 
  
−
<pre>
+
<li>
−
o-------------------------------------------------o
+
<p>The ''linear propositions'', <math>\{ \ell : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{\ell} \mathbb{B}),\!</math> may be written as sums:</p>
−
|                                                |
 
−
|                                                |
 
−
|          o-----------o  o-----------o          |
 
−
|        /            \ /            \         |
 
−
|        /      x      o      y      \       |
 
−
|      /              /`\               \       |
 
−
|      /              /```\               \     |
 
−
|    o              o`````o              o    |
 
−
|    |              |`````|              |    |
 
−
|    |        dy    |`````|    dx        |    |
 
−
|    |    <---------|--o--|--------->    |    |
 
−
|    |              |`````|              |    |
 
−
|    |              |`````|              |    |
 
−
|    o              o`````o              o    |
 
−
|      \               \```/              /      |
 
−
|      \               \`/               /      |
 
−
|        \              o              /        |
 
−
|        \            / \            /        |
 
−
|          o-----------o  o-----------o          |
 
−
|                                                |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
We can form propositions from these differential variables in the same way that we would any other logical variables, for instance, interpreting the proposition (''dx'' (''dy'')) to say "''dx''&nbsp;&rArr;&nbsp;''dy''", in other words, however you wish to take it, whether indicatively or injunctively, as saying something to the effect that there is "no change in x without a change in y".
+
{| align="center" cellspacing="8" width="90%"
 +
|
 +
<math>\sum_{i=1}^n e_i ~=~ e_1 + \ldots + e_n
 +
~\text{where}~
 +
\left\{\begin{matrix} e_i = a_i \\ \text{or} \\ e_i = 0 \end{matrix}\right\}
 +
~\text{for}~ i = 1 ~\text{to}~ n.\!</math>
 +
|}
 +
</li>
  
−
Given the proposition ''f''(''x'', ''y'') in ''U'' = ''X''&nbsp; &times;&nbsp;''Y'', the (''first order'') ''enlargement'' of ''f'' is the proposition ''Ef'' in ''EU'' that is defined by the formula ''Ef''(''x'', ''y'', ''dx'', ''dy'') = ''f''(''x'' + ''dx'', ''y'' + ''dy'').
+
<li>
 +
<p>The ''positive propositions'', <math>\{ p : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{p} \mathbb{B}),\!</math> may be written as products:</p>
  
−
In the example ''f''(''x'', ''y'') = ''xy'', we obtain:
+
{| align="center" cellspacing="8" width="90%"
 +
|
 +
<math>\prod_{i=1}^n e_i ~=~ e_1 \cdot \ldots \cdot e_n
 +
~\text{where}~
 +
\left\{\begin{matrix} e_i = a_i \\ \text{or} \\ e_i = 1 \end{matrix}\right\}
 +
~\text{for}~ i = 1 ~\text{to}~ n.\!</math>
 +
|}
 +
</li>
  
−
: ''Ef''(''x'', ''y'', ''dx'', ''dy'') = (''x'' + ''dx'')(''y'' + ''dy'').
+
<li>
 +
<p>The ''singular propositions'', <math>\{ \mathbf{x} : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{s} \mathbb{B}),\!</math> may be written as products:</p>
  
−
<pre>
+
{| align="center" cellspacing="8" width="90%"
−
o-------------------------------------------------o
+
|
−
|                                                |
+
<math>\prod_{i=1}^n e_i ~=~ e_1 \cdot \ldots \cdot e_n
−
|                  x  dx y  dy                  |
+
~\text{where}~
−
|                  o---o o---o                  |
+
\left\{\begin{matrix} e_i = a_i \\ \text{or} \\ e_i = \texttt{(} a_i \texttt{)} \end{matrix}\right\}
−
|                    \ | |  /                    |
+
~\text{for}~ i = 1 ~\text{to}~ n.\!</math>
−
|                    \ | | /                    |
+
|}
−
|                      \| |/                      |
+
</li>
−
|                      @=@                      |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Ef =           (x, dx) (y, dy)                |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
Given the proposition ''f''(''x'', ''y'') in ''U'' = ''X''&nbsp;&times;&nbsp;''Y'', the (''first order'') ''difference'' of ''f'' is the proposition ''Df'' in ''EU'' that is defined by the formula ''Df'' = ''Ef''&nbsp;&ndash;&nbsp;''f'', or, written out in full, ''Df''(''x'', ''y'', ''dx'', ''dy'') = ''f''(''x'' + ''dx'', ''y'' + ''dy'')&nbsp;&ndash;&nbsp;''f''(''x'', ''y'').
+
</ul>
  
−
In the example ''f''(''x'', ''y'') = ''xy'', the result is:
+
In each case the rank <math>k\!</math> ranges from <math>0\!</math> to <math>n\!</math> and counts the number of positive appearances of the coordinate propositions <math>a_1, \ldots, a_n\!</math> in the resulting expression.  For example, for <math>n = 3,~\!</math> the linear proposition of rank <math>0\!</math> is <math>0,\!</math> the positive proposition of rank <math>0\!</math> is <math>1,\!</math> and the singular proposition of rank <math>0\!</math> is <math>\texttt{(} a_1 \texttt{)} \texttt{(} a_2 \texttt{)} \texttt{(} a_3 \texttt{)}.\!</math>
  
−
* ''Df''(''x'', ''y'', ''dx'', ''dy'') = (''x'' + ''dx'')(''y'' + ''dy'')&nbsp;&ndash;&nbsp;''xy''.
+
The basic propositions <math>a_i : \mathbb{B}^n \to \mathbb{B}\!</math> are both linear and positive.  So these two kinds of propositions, the linear and the positive, may be viewed as two different ways of generalizing the class of basic propositions.
  
−
<pre>
+
Finally, it is important to note that all of the above distinctions are relative to the choice of a particular logical basis <math>\mathcal{A} = \{ a_1, \ldots, a_n \}.\!</math>  For example, a singular proposition with respect to the basis <math>\mathcal{A}\!</math> will not remain singular if <math>\mathcal{A}\!</math> is extended by a number of new and independent features.  Even if one keeps to the original set of pairwise options <math>\{ a_i \} \cup \{ \texttt{(} a_i \texttt{)} \}\!</math> to pick out a new basis, the sets of linear propositions and positive propositions are both determined by the choice of basic propositions, and this whole determination is tantamount to the purely conventional choice of a cell as origin.
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|            x dx y  dy                        |
 
−
|            o---o o---o                        |
 
−
|              \ | |  /                          |
 
−
|              \ | | /                           |
 
−
|                \| |/        x y                |
 
−
|                o=o-----------o                |
 
−
|                  \           /                 |
 
−
|                  \         /                  |
 
−
|                    \       /                    |
 
−
|                    \     /                    |
 
−
|                      \   /                      |
 
−
|                      \ /                      |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Df =          ((x, dx)(y, dy), xy)            |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
We did not yet go through the trouble to interpret this (first order) ''difference of conjunction'' fully, but were happy simply to evaluate it with respect to a single location in the universe of discourse, namely, at the point picked out by the singular proposition ''xy'', in as much as if to say, at the place where ''x'' = 1 and ''y'' = 1.  This evaluation is written in the form ''Df''|''xy'' or ''Df''|<1, 1>, and we arrived at the locally applicable law that states that ''f'' = ''xy'' = ''x'' & ''y'' &rArr; ''Df''|''xy'' = ((''dx'')(''dy'')) = ''dx'' or ''dy''.
+
===Differential Extensions===
  
−
<pre>
+
An initial universe of discourse, <math>A^\bullet,</math> supplies the groundwork for any number of further extensions, beginning with the ''first order differential extension'', <math>\mathrm{E}A^\bullet.</math> The construction of <math>\mathrm{E}A^\bullet</math> can be described in the following stages:
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                                                |
 
−
|          o-----------o  o-----------o          |
 
−
|        /            \ /             \         |
 
−
|        /      x      o      y      \       |
 
−
|      /               /`\              \      |
 
−
|      /              /```\              \      |
 
−
|    o              o`````o              o    |
 
−
|    |              |`````|              |    |
 
−
|    |      dy (dx)  |`````| dx (dy)      |    |
 
−
|    |  o<----------|--o--|---------->o  |    |
 
−
|    |              |``|``|              |    |
 
−
|    |              |``|``|              |    |
 
−
|    o              o``|``o              o    |
 
−
|      \              \`|`/              /      |
 
−
|      \              \|/              /      |
 
−
|        \               |              /        |
 
−
|        \            /|\            /        |
 
−
|          o-----------o | o-----------o          |
 
−
|                        |                        |
 
−
|                      dx|dy                      |
 
−
|                        |                        |
 
−
|                        v                        |
 
−
|                        o                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                    dx  dy                    |
 
−
|                      o  o                      |
 
−
|                      \ /                      |
 
−
|                        o                        |
 
−
|                        |                        |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Df|xy =          ((dx) (dy))                  |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
The picture illustrates the analysis of the inclusive disjunction ((''dx'')(''dy'')) into the exclusive disjunction:  ''dx''(''dy'') + ''dy''(''dx'') + ''dx dy'', a proposition that may be interpreted to say "change x or change y or both".  And this can be recognized as just what you need to do if you happen to find yourself in the center cell and desire a detailed description of ways to depart it.
+
<ul>
  
−
===Note 3===
+
<li>
 +
<p>The initial alphabet, <math>\mathfrak{A} = \{ {}^{\backprime\backprime} a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} a_n {}^{\prime\prime} \},\!</math> is extended by a ''first order differential alphabet'', <math>\mathrm{d}\mathfrak{A} = \{ {}^{\backprime\backprime} \mathrm{d}a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} \mathrm{d}a_n {}^{\prime\prime} \},\!</math> resulting in a ''first order extended alphabet'', <math>\mathrm{E}\mathfrak{A},</math> defined as follows:</p>
  
−
Last time we computed what will variously be called the ''difference map'', the ''difference proposition'', or the ''local proposition'' ''Df''<sub>''p''</sub> for the proposition ''f''(''x'',&nbsp;''y'') = ''xy'' at the point ''p'' where ''x'' = 1 and ''y'' = 1.
+
{| align="center" cellspacing="8" width="90%"
 +
|
 +
<math>\mathrm{E}\mathfrak{A} ~=~ \mathfrak{A} ~\cup~ \mathrm{d}\mathfrak{A} ~=~ \{ {}^{\backprime\backprime} a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} a_n {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{d}a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} \mathrm{d}a_n {}^{\prime\prime} \}.\!</math>
 +
|}
 +
</li>
  
−
In the universe ''U'' = ''X''&nbsp;&times;&nbsp;''Y'', the four propositions ''xy'', ''x''(''y''), (''x'')''y'', (''x'')(''y'') that indicate the "cells", or the smallest regions of the venn diagram, are called ''singular propositions''.  These serve as an alternative notation for naming the points <1,&nbsp;1>, <1,&nbsp;0>, <0,&nbsp;1>, <0,&nbsp;0>, respectively.
+
<li>
 +
<p>The initial basis, <math>\mathcal{A} = \{ a_1, \ldots, a_n \},\!</math> is extended by a ''first order differential basis'', <math>\mathrm{d}\mathcal{A} = \{ \mathrm{d}a_1, \ldots, \mathrm{d}a_n \},\!</math> resulting in a ''first order extended basis'', <math>\mathrm{E}\mathcal{A},\!</math> defined as follows:</p>
  
−
Thus, we can write ''Df''<sub>''p''</sub> = ''Df''|''p'' = ''Df''|<1, 1> = ''Df''|''xy'', so long as we know the frame of reference in force.
+
{| align="center" cellspacing="8" width="90%"
 +
|
 +
<math>\mathrm{E}\mathcal{A} ~=~ \mathcal{A} ~\cup~ \mathrm{d}\mathcal{A} ~=~ \{ a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \}.\!</math>
 +
|}
 +
</li>
  
−
Sticking with the example ''f''(''x'',&nbsp;''y'') = ''xy'', let us compute the value of the difference proposition ''Df'' at all of the points.
+
<li>
 +
<p>The initial space, <math>A = \langle a_1, \ldots, a_n \rangle,\!</math> is extended by a ''first order differential space'' or ''tangent space'', <math>\mathrm{d}A = \langle \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle,\!</math> at each point of <math>A,\!</math> resulting in a ''first order extended space'' or ''tangent bundle space'', <math>\mathrm{E}A,\!</math> defined as follows:</p>
  
−
<pre>
+
{| align="center" cellspacing="8" width="90%"
−
o-------------------------------------------------o
+
|
−
|                                                 |
+
<math>\mathrm{E}A ~=~ A ~\times~ \mathrm{d}A ~=~ \langle \mathrm{E}\mathcal{A} \rangle ~=~ \langle \mathcal{A} \cup \mathrm{d}\mathcal{A} \rangle ~=~ \langle a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle.\!</math>
−
|            x  dx y  dy                        |
+
|}
−
|            o---o o---o                        |
+
</li>
−
|              \  | |  /                          |
 
−
|              \ | | /                          |
 
−
|                \| |/        x y                |
 
−
|                o=o-----------o                |
 
−
|                  \          /                  |
 
−
|                  \        /                  |
 
−
|                    \      /                    |
 
−
|                    \    /                    |
 
−
|                      \  /                      |
 
−
|                      \ /                      |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Df =        ((x, dx)(y, dy), xy)                |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
<pre>
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                dx    dy                        |
 
−
|            o---o o---o                        |
 
−
|              \ | |  /                          |
 
−
|              \ | | /                          |
 
−
|                \| |/                            |
 
−
|                o=o-----------o                |
 
−
|                  \           /                  |
 
−
|                  \        /                  |
 
−
|                    \      /                    |
 
−
|                    \     /                    |
 
−
|                      \   /                      |
 
−
|                      \ /                      |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Df|xy =           ((dx) (dy))                  |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
<pre>
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                  o                            |
 
−
|                dx |  dy                        |
 
−
|            o---o o---o                        |
 
−
|              \ | |  /                          |
 
−
|              \ | | /        o                |
 
−
|                \| |/          |                |
 
−
|                o=o-----------o                |
 
−
|                  \          /                  |
 
−
|                  \         /                  |
 
−
|                    \       /                    |
 
−
|                    \     /                    |
 
−
|                      \   /                      |
 
−
|                      \ /                      |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Df|x(y) =         (dx) dy                      |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
<pre>
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|            o                                  |
 
−
|            |  dx    dy                        |
 
−
|            o---o o---o                        |
 
−
|              \ | |  /                          |
 
−
|              \ | | /        o                |
 
−
|                \| |/          |                |
 
−
|                o=o-----------o                |
 
−
|                  \           /                  |
 
−
|                  \         /                  |
 
−
|                    \       /                    |
 
−
|                    \    /                    |
 
−
|                      \  /                      |
 
−
|                      \ /                      |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Df|(x)y =            dx (dy)                    |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
<pre>
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|            o    o                            |
 
−
|            |  dx |  dy                        |
 
−
|            o---o o---o                        |
 
−
|              \  | |  /                          |
 
−
|               \ | | /      o  o              |
 
−
|                \| |/        \ /                |
 
−
|                o=o-----------o                |
 
−
|                  \          /                  |
 
−
|                  \        /                  |
 
−
|                    \      /                    |
 
−
|                    \    /                    |
 
−
|                      \  /                      |
 
−
|                      \ /                      |
 
−
|                        @                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Df|(x)(y) =          dx dy                      |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
The easy way to visualize the values of these graphical expressions is just to notice the following equivalents:
+
<li>
 +
<p>Finally, the initial universe, <math>A^\bullet = [ a_1, \ldots, a_n ],\!</math> is extended by a ''first order differential universe'' or ''tangent universe'', <math>\mathrm{d}A^\bullet = [ \mathrm{d}a_1, \ldots, \mathrm{d}a_n ],\!</math> at each point of <math>A^\bullet,\!</math> resulting in a ''first order extended universe'' or ''tangent bundle universe'', <math>\mathrm{E}A^\bullet,\!</math> defined as follows:</p>
  
−
<pre>
+
{| align="center" cellspacing="8" width="90%"
−
o-------------------------------------------------o
+
|
−
|                                                |
+
<math>\mathrm{E}A^\bullet ~=~ [ \mathrm{E}\mathcal{A} ] ~=~ [ \mathcal{A} ~\cup~ \mathrm{d}\mathcal{A} ] ~=~ [ a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n ].\!</math>
−
|  x                                              |
+
|}
−
|  o-o-o-...-o-o-o                                |
 
−
|  \           /                                |
 
−
|    \         /                                  |
 
−
|    \       /                                  |
 
−
|      \     /                          x        |
 
−
|      \   /                          o        |
 
−
|        \ /                            |        |
 
−
|        @              =             @        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|  (x, , ... , , )      =            (x)        |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
<pre>
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                o                                |
 
−
| x_1 x_2  x_k  |                                |
 
−
|  o---o-...-o---o                                |
 
−
|  \           /                                |
 
−
|    \         /                                  |
 
−
|    \       /                                   |
 
−
|     \    /                                    |
 
−
|      \  /                                    |
 
−
|        \ /                      x_1 ... x_k    |
 
−
|        @              =              @        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|  (x_1, ..., x_k, ())  =        x_1 ... x_k    |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
Laying out the arrows on the augmented venn diagram, one gets a picture of a ''differential vector field''.
+
<p>This gives <math>\mathrm{E}A^\bullet\!</math> the type:</p>
  
−
<pre>
+
{| align="center" cellspacing="8" width="90%"
−
o-------------------------------------------------o
+
|
−
|                                                |
+
<math>[ \mathbb{B}^n \times \mathbb{D}^n ] ~=~ (\mathbb{B}^n \times \mathbb{D}^n\ +\!\!\to \mathbb{B}) ~=~ (\mathbb{B}^n \times \mathbb{D}^n, \mathbb{B}^n \times \mathbb{D}^n \to \mathbb{B}).\!</math>
−
|                        o                        |
+
|}
−
|                        |                        |
+
</li>
−
|                      dx|dy                      |
 
−
|                        |                        |
 
−
|          o-----------o | o-----------o          |
 
−
|        /            \|/            \         |
 
−
|        /      x      |      y      \       |
 
−
|      /              /|\               \       |
 
−
|      /              /`|`\               \     |
 
−
|    o              o``|``o              o    |
 
−
|    |      dy (dx) |``v``|  dx (dy)      |    |
 
−
|    |  o-----------|->o<-|-----------o  |    |
 
−
|    |              |`````|              |    |
 
−
|    |  o<----------|--o--|---------->o  |    |
 
−
|    |      dy (dx)  |``|``|  dx (dy)      |    |
 
−
|    o              o``|``o              o    |
 
−
|      \               \`|`/              /      |
 
−
|      \               \|/              /      |
 
−
|        \               |              /        |
 
−
|        \             /|\             /         |
 
−
|         o-----------o | o-----------o          |
 
−
|                        |                        |
 
−
|                      dx|dy                      |
 
−
|                        |                        |
 
−
|                        v                        |
 
−
|                        o                        |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
This really just constitutes a depiction of the interpretations in ''EU'' = ''X''&nbsp;&times;&nbsp;''Y''&nbsp;&times;&nbsp;''dX''&nbsp;&times;&nbsp;''dY'' that satisfy the difference proposition ''Df'', namely, these:
+
</ul>
  
−
<pre>
+
A proposition in a differential extension of a universe of discourse is called a ''differential proposition'' and forms the analogue of a system of differential equations in ordinary calculus.  With these constructions, the first order extended universe <math>\mathrm{E}A^\bullet</math> and the first order differential proposition <math>f : \mathrm{E}A \to \mathbb{B},</math> we have arrived, in concept at least, at the foothills of [[differential logic]].
−
1.  x  y  dx  dy
 
−
2.  x  y  dx (dy)
 
−
3.  x  y (dx) dy
 
−
4.  x (y)(dx) dy
 
−
5.  (x) y  dx (dy)
 
−
6.  (x)(y) dx  dy
 
−
</pre>
 
  
−
By inspection, it is fairly easy to understand ''Df'' as telling you what you have to do from each point of ''U'' in order to change the value borne by ''f''(''x'',&nbsp;''y'').
+
Table&nbsp;7 summarizes the notations that are needed to describe the first order differential extensions of propositional calculi in a systematic manner.
  
−
===Note 4===
+
<br>
  
−
We have been studying the action of the difference operator ''D'', also known as the ''localization operator'', on the proposition ''f''&nbsp;:&nbsp;''X''&nbsp;&times;&nbsp;''Y''&nbsp;&rarr;&nbsp;'''B''' that is commonly known as the conjunction ''xy''.  We described ''Df'' as a (first order) differential proposition, that is, a proposition of the type ''Df''&nbsp;:&nbsp;''X''&nbsp;&times;&nbsp;''Y''&nbsp;&times;&nbsp;''dX''&nbsp;&times;&nbsp;''dY''&nbsp;&rarr;&nbsp;'''B'''.  Abstracting from the augmented venn diagram that illustrates how the ''models'', or the ''satisfying interpretations'', of ''Df'' distribute within the extended universe ''EU'' = ''X''&nbsp;&times;&nbsp;''Y''&nbsp;&times;&nbsp;''dX''&nbsp;&times;&nbsp;''dY'', we can depict ''Df'' in the form of a ''digraph'' or ''directed graph'', one whose points are labeled with the elements of ''U'' =  ''X''&nbsp;&times;&nbsp;''Y'' and whose arrows are labeled with the elements of ''dU'' = ''dX''&nbsp;&times;&nbsp;''dY''.
+
{| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:75%"
 +
|+ style="height:30px" | <math>\text{Table 7.} ~~ \text{Differential Extension : Basic Notation}\!</math>
 +
|- style="height:40px; background:ghostwhite"
 +
| <math>\text{Symbol}\!</math>
 +
| <math>\text{Notation}\!</math>
 +
| <math>\text{Description}\!</math>
 +
| <math>\text{Type}\!</math>
 +
|-
 +
| <math>\mathrm{d}\mathfrak{A}\!</math>
 +
| <math>\{ {}^{\backprime\backprime} \mathrm{d}a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} \mathrm{d}a_n {}^{\prime\prime} \}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{Alphabet of}
 +
\\[2pt]
 +
\text{differential symbols}
 +
\end{matrix}</math>
 +
| <math>[n] = \mathbf{n}\!</math>
 +
|-
 +
| <math>\mathrm{d}\mathcal{A}\!</math>
 +
| <math>\{ \mathrm{d}a_1, \ldots, \mathrm{d}a_n \}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{Basis of}
 +
\\[2pt]
 +
\text{differential features}
 +
\end{matrix}</math>
 +
| <math>[n] = \mathbf{n}\!</math>
 +
|-
 +
| <math>\mathrm{d}A_i\!</math>
 +
| <math>\{ \texttt{(} \mathrm{d}a_i \texttt{)}, \mathrm{d}a_i \}\!</math>
 +
| <math>\text{Differential dimension}~ i\!</math>
 +
| <math>\mathbb{D}\!</math>
 +
|-
 +
| <math>\mathrm{d}A\!</math>
 +
|
 +
<math>\begin{matrix}
 +
\langle \mathrm{d}\mathcal{A} \rangle
 +
\\[2pt]
 +
\langle \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle
 +
\\[2pt]
 +
\{ (\mathrm{d}a_1, \ldots, \mathrm{d}a_n) \}
 +
\\[2pt]
 +
\mathrm{d}A_1 \times \ldots \times \mathrm{d}A_n
 +
\\[2pt]
 +
\textstyle \prod_i \mathrm{d}A_i
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{Tangent space at a point:}
 +
\\[2pt]
 +
\text{Set of changes, motions,}
 +
\\[2pt]
 +
\text{steps, tangent vectors}
 +
\\[2pt]
 +
\text{at a point}
 +
\end{matrix}</math>
 +
| <math>\mathbb{D}^n\!</math>
 +
|-
 +
| <math>\mathrm{d}A^*\!</math>
 +
| <math>(\mathrm{hom} : \mathrm{d}A \to \mathbb{B})\!</math>
 +
| <math>\text{Linear functions on}~ \mathrm{d}A\!</math>
 +
| <math>(\mathbb{D}^n)^* \cong \mathbb{D}^n\!</math>
 +
|-
 +
| <math>\mathrm{d}A^\uparrow\!</math>
 +
| <math>(\mathrm{d}A \to \mathbb{B})\!</math>
 +
| <math>\text{Boolean functions on}~ \mathrm{d}A\!</math>
 +
| <math>\mathbb{D}^n \to \mathbb{B}\!</math>
 +
|-
 +
| <math>\mathrm{d}A^\bullet\!</math>
 +
|
 +
<math>\begin{matrix}
 +
[\mathrm{d}\mathcal{A}]
 +
\\[2pt]
 +
(\mathrm{d}A, \mathrm{d}A^\uparrow)
 +
\\[2pt]
 +
(\mathrm{d}A ~+\!\to \mathbb{B})
 +
\\[2pt]
 +
(\mathrm{d}A, (\mathrm{d}A \to \mathbb{B}))
 +
\\[2pt]
 +
[\mathrm{d}a_1, \ldots, \mathrm{d}a_n]
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{Tangent universe at a point of}~ A^\bullet,
 +
\\[2pt]
 +
\text{based on the tangent features}
 +
\\[2pt]
 +
\{ \mathrm{d}a_1, \ldots, \mathrm{d}a_n \}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
(\mathbb{D}^n, (\mathbb{D}^n \to \mathbb{B}))
 +
\\[2pt]
 +
(\mathbb{D}^n ~+\!\to \mathbb{B})
 +
\\[2pt]
 +
[\mathbb{D}^n]
 +
\end{matrix}</math>
 +
|}
  
−
<pre>
+
<br>
−
o-------------------------------------------------o
 
−
|  f =                  x y                      |
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
| Df =              x  y  ((dx)(dy))              |
 
−
|                                                |
 
−
|          +      x (y)  (dx) dy                |
 
−
|                                                |
 
−
|          +      (x) y    dx (dy)              |
 
−
|                                                |
 
−
|          +      (x)(y)  dx  dy                |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                      x y                      |
 
−
|  x (y) o<------------->o<------------->o (x) y  |
 
−
|            (dx) dy    ^    dx (dy)            |
 
−
|                        |                        |
 
−
|                        |                        |
 
−
|                    dx | dy                    |
 
−
|                        |                        |
 
−
|                        |                        |
 
−
|                        v                        |
 
−
|                        o                        |
 
−
|                    (x) (y)                    |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
</pre>
 
  
−
Any proposition worth its salt has many equivalent ways to view it, any one of which may reveal some unsuspected aspect of its meaning.  We will encounter more and more of these variant readings as we go.
+
'''&hellip;'''
  
−
===Note 5===
+
==Appendices==
  
−
The enlargement operator ''E'', also known as the ''shift operator'', has many interesting and very useful properties in its own right, so let us not fail to observe a few of the more salient features that play out on the surface of our simple example, ''f''(''x'',&nbsp;''y'') = ''xy''.
+
===Appendix 1. Propositional Forms and Differential Expansions===
  
−
Introduce a suitably generic definition of the extended universe of discourse:
+
====Table A1. Propositional Forms on Two Variables====
  
−
: Let ''U'' = ''X''<sub>1</sub>&nbsp;&times;&nbsp;&hellip;&nbsp;&times;&nbsp;''X''<sub>''k''</sub> and ''EU'' = ''U''&nbsp;&times;&nbsp;''dU'' = ''X''<sub>1</sub>&nbsp;&times;&nbsp;&hellip;&nbsp;&times;&nbsp;''X''<sub>''k''</sub>&nbsp;&times;&nbsp;''dX''<sub>1</sub>&nbsp;&times;&nbsp;&hellip;&nbsp;&times;&nbsp;''dX''<sub>''k''</sub>.
+
<br>
  
−
For a proposition ''f''&nbsp;:&nbsp;''X''<sub>1</sub>&nbsp;&times;&nbsp;&hellip;&nbsp;&times;&nbsp;''X''<sub>''k''</sub>&nbsp;&rarr;&nbsp;'''B''', the (first order) enlargement of f is the proposition ''Ef''&nbsp;:&nbsp;''EU''&nbsp;&rarr;&nbsp;'''B''' that is defined by:
+
{| align="center" border="1" cellpadding="6" cellspacing="0" style="text-align:center; width:80%"
 +
|+ style="height:30px" | <math>\text{Table A1.} ~~ \text{Propositional Forms on Two Variables}\!</math>
 +
|- style="background:ghostwhite"
 +
| width="15%" | <math>\begin{matrix}\mathcal{L}_1\\\text{Decimal}\\\text{Index}\end{matrix}</math>
 +
| width="15%" | <math>\begin{matrix}\mathcal{L}_2\\\text{Binary}\\\text{Index}\end{matrix}</math>
 +
| width="15%" | <math>\begin{matrix}\mathcal{L}_3\\\text{Truth}\\\text{Table}\end{matrix}</math>
 +
| width="15%" | <math>\begin{matrix}\mathcal{L}_4\\\text{Cactus}\\\text{Language}\end{matrix}</math>
 +
| width="25%" | <math>\begin{matrix}\mathcal{L}_5\\\text{English}\\\text{Paraphrase}\end{matrix}</math>
 +
| width="15%" | <math>\begin{matrix}\mathcal{L}_6\\\text{Conventional}\\\text{Formula}\end{matrix}</math>
 +
|- style="background:ghostwhite"
 +
| &nbsp;
 +
| align="right" | <math>x\colon\!</math>
 +
| <math>1~1~0~0\!</math>
 +
| &nbsp; || &nbsp; || &nbsp;
 +
|- style="background:ghostwhite"
 +
| &nbsp;
 +
| align="right" | <math>y\colon\!</math>
 +
| <math>1~0~1~0\!</math>
 +
| &nbsp; || &nbsp; || &nbsp;
 +
|-
 +
|
 +
<math>\begin{matrix}
 +
f_{0}\\f_{1}\\f_{2}\\f_{3}\\f_{4}\\f_{5}\\f_{6}\\f_{7}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
f_{0000}\\f_{0001}\\f_{0010}\\f_{0011}\\f_{0100}\\f_{0101}\\f_{0110}\\f_{0111}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
0~0~0~0\\0~0~0~1\\0~0~1~0\\0~0~1~1\\0~1~0~0\\0~1~0~1\\0~1~1~0\\0~1~1~1
 +
\end{matrix}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
\texttt{(~)}
 +
\\
 +
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\\
 +
\texttt{(} x \texttt{)~ ~}
 +
\\
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\\
 +
\texttt{~ ~(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{,~} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{~~} y \texttt{)}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{false}
 +
\\
 +
\text{neither}~ x ~\text{nor}~ y
 +
\\
 +
y ~\text{without}~ x
 +
\\
 +
\text{not}~ x
 +
\\
 +
x ~\text{without}~ y
 +
\\
 +
\text{not}~ y
 +
\\
 +
x ~\text{not equal to}~ y
 +
\\
 +
\text{not both}~ x ~\text{and}~ y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
0
 +
\\
 +
\lnot x \land \lnot y
 +
\\
 +
\lnot x \land y
 +
\\
 +
\lnot x
 +
\\
 +
x \land \lnot y
 +
\\
 +
\lnot y
 +
\\
 +
x \ne y
 +
\\
 +
\lnot x \lor \lnot y
 +
\end{matrix}</math>
 +
|-
 +
|
 +
<math>\begin{matrix}
 +
f_{8}\\f_{9}\\f_{10}\\f_{11}\\f_{12}\\f_{13}\\f_{14}\\f_{15}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
f_{1000}\\f_{1001}\\f_{1010}\\f_{1011}\\f_{1100}\\f_{1101}\\f_{1110}\\f_{1111}
 +
\end{matrix}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
1~0~0~0\\1~0~0~1\\1~0~1~0\\1~0~1~1\\1~1~0~0\\1~1~0~1\\1~1~1~0\\1~1~1~1
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\texttt{~~} x \texttt{~~} y \texttt{~~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\\
 +
\texttt{~ ~ ~} y \texttt{~~}
 +
\\
 +
\texttt{~(} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{~~} x \texttt{~ ~ ~}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\\
 +
\texttt{((~))}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
x ~\text{and}~ y
 +
\\
 +
x ~\text{equal to}~ y
 +
\\
 +
y
 +
\\
 +
\text{not}~ x ~\text{without}~ y
 +
\\
 +
x
 +
\\
 +
\text{not}~ y ~\text{without}~ x
 +
\\
 +
x ~\text{or}~ y
 +
\\
 +
\text{true}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
x \land y
 +
\\
 +
x = y
 +
\\
 +
y
 +
\\
 +
x \Rightarrow y
 +
\\
 +
x
 +
\\
 +
x \Leftarrow y
 +
\\
 +
x \lor y
 +
\\
 +
1
 +
\end{matrix}</math>
 +
|}
  
−
: ''Ef''(''x''<sub>1</sub>,&nbsp;&hellip;,&nbsp;''x''<sub>''k''</sub>, ''dx''<sub>1</sub>,&nbsp;&hellip;,&nbsp;''dx''<sub>''k''</sub>) = ''f''(''x''<sub>1</sub>&nbsp;+&nbsp;''dx''<sub>1</sub>,&nbsp;&hellip;,&nbsp;''x''<sub>''k''</sub>&nbsp;+&nbsp;''dx''<sub>''k''</sub>).
+
<br>
  
−
It should be noted that the so-called ''differential variables'' ''dx''<sub>''j''</sub> are really just the same kind of boolean variables as the other ''x''<sub>''j''</sub>.  It is conventional to give the additional variables these brands of inflected names, but whatever extra connotations we might choose to attach to these syntactic conveniences are wholly external to their purely algebraic meanings.
+
====Table A2. Propositional Forms on Two Variables====
  
−
For the example ''f''(''x'', ''y'') = ''xy'', we obtain:
+
<br>
−
 
 
−
: ''Ef''(''x'', ''y'', ''dx'', ''dy'') = (''x'' + ''dx'')(''y'' + ''dy'').
 
−
 
 
−
Given that this expression uses nothing more than the boolean ring operations of addition (+) and multiplication (&middot;), it is permissible to multiply things out in the usual manner to arrive at the result:
 
−
 
 
−
: ''Ef''(''x'', ''y'', ''dx'', ''dy'') = ''x y'' + ''x dy'' + ''y dx'' + ''dx dy''
 
−
 
 
−
To understand what this means in logical terms, for instance, as expressed in a boolean expansion or a ''disjunctive normal form'' (DNF), it is perhaps a little better to go back and analyze the expression the same way that we did for ''Df''.  Thus, let us compute the value of the enlarged proposition ''Ef'' at each of the points in the universe of discourse ''U'' = ''X''&nbsp;&times;&nbsp;''Y''.
 
−
 
 
−
<pre>
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                  x  dx y  dy                  |
 
−
|                  o---o o---o                  |
 
−
|                    \  | |  /                    |
 
−
|                    \ | | /                    |
 
−
|                      \| |/                      |
 
−
|                      @=@                      |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Ef =            (x, dx) (y, dy)                |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
<pre>
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                      dx    dy                  |
 
−
|                  o---o o---o                  |
 
−
|                    \  | |  /                    |
 
−
|                    \ | | /                    |
 
−
|                      \| |/                      |
 
−
|                      @=@                      |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Ef|xy =            (dx) (dy)                    |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
<pre>
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                        o                      |
 
−
|                      dx |  dy                  |
 
−
|                  o---o o---o                  |
 
−
|                    \  | |  /                    |
 
−
|                    \ | | /                    |
 
−
|                      \| |/                      |
 
−
|                      @=@                      |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Ef|x(y) =          (dx)  dy                    |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
<pre>
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                  o                            |
 
−
|                  |  dx    dy                  |
 
−
|                  o---o o---o                  |
 
−
|                    \  | |  /                    |
 
−
|                    \ | | /                    |
 
−
|                      \| |/                      |
 
−
|                      @=@                      |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Ef|(x)y =          dx  (dy)                    |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
<pre>
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                  o    o                      |
 
−
|                  |  dx |  dy                  |
 
−
|                  o---o o---o                  |
 
−
|                    \  | |  /                    |
 
−
|                    \ | | /                    |
 
−
|                      \| |/                      |
 
−
|                      @=@                      |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
| Ef|(x)(y) =        dx  dy                    |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
 
 
−
Given the sort of data that arises from this form of analysis, we can now fold the disjoined ingredients back into a boolean expansion or a DNF that is equivalent to the proposition ''Ef''.
 
−
 
 
−
: ''Ef'' = ''xy Ef''<sub>''xy''</sub> + ''x''(''y'') ''Ef''<sub>''x''(''y'')</sub> + (''x'')''y Ef''<sub>(''x'')''y''</sub> + (''x'')(''y'') ''Ef''<sub>(''x'')(''y'')</sub>
 
−
 
 
−
Here is a summary of the result, illustrated by means of a digraph picture, where the "no change" element (''dx'')(''dy'') is drawn as a loop at the point ''x y''.
 
  
−
<pre>
+
{| align="center" border="1" cellpadding="6" cellspacing="0" style="text-align:center; width:80%"
−
o-------------------------------------------------o
+
|+ style="height:30px" | <math>\text{Table A2.} ~~ \text{Propositional Forms on Two Variables}\!</math>
−
|  f =                  x y                      |
+
|- style="background:ghostwhite"
−
o-------------------------------------------------o
+
| width="15%" | <math>\begin{matrix}\mathcal{L}_1\\\text{Decimal}\\\text{Index}\end{matrix}</math>
−
|                                                |
+
| width="15%" | <math>\begin{matrix}\mathcal{L}_2\\\text{Binary}\\\text{Index}\end{matrix}</math>
−
| Ef =              x  y  (dx)(dy)              |
+
| width="15%" | <math>\begin{matrix}\mathcal{L}_3\\\text{Truth}\\\text{Table}\end{matrix}</math>
−
|                                                |
+
| width="15%" | <math>\begin{matrix}\mathcal{L}_4\\\text{Cactus}\\\text{Language}\end{matrix}</math>
−
|          +      x (y)  (dx) dy                |
+
| width="25%" | <math>\begin{matrix}\mathcal{L}_5\\\text{English}\\\text{Paraphrase}\end{matrix}</math>
−
|                                                |
+
| width="15%" | <math>\begin{matrix}\mathcal{L}_6\\\text{Conventional}\\\text{Formula}\end{matrix}</math>
−
|          +      (x) y    dx (dy)              |
+
|- style="background:ghostwhite"
−
|                                                |
 
−
|          +      (x)(y)  dx  dy                |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
|                                                |
 
−
|                    (dx) (dy)                    |
 
−
|                    .--->---.                    |
 
−
|                    \    /                    |
 
−
|                      \x y/                      |
 
−
|                      \ /                      |
 
−
|  x (y) o-------------->o<--------------o (x) y  |
 
−
|            (dx) dy    ^    dx (dy)            |
 
−
|                        |                        |
 
−
|                        |                        |
 
−
|                    dx | dy                    |
 
−
|                        |                        |
 
−
|                        |                        |
 
−
|                        |                        |
 
−
|                        o                        |
 
−
|                    (x) (y)                    |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
</pre>
 
−
 
 
−
We may understand the enlarged proposition ''Ef'' as telling us all the different ways to reach a model of ''f'' from any point of the universe ''U''.
 
−
 
 
−
===Note 6===
 
−
 
 
−
To broaden our experience with simple examples, let us now contemplate the sixteen functions of concrete type ''X''&nbsp;&times;&nbsp;''Y''&nbsp;&rarr;&nbsp;'''B''' and abstract type '''B'''&nbsp;&times;&nbsp;'''B'''&nbsp;&rarr;&nbsp;'''B'''.  For future reference, I will set here a few tables that detail the actions of ''E'' and ''D'' and on each of these functions, allowing us to view the results in several different ways.
 
−
 
 
−
By way of initial orientation, Table 1 lists equivalent expressions for the sixteen functions in a number of different languages for zeroth order logic.
 
−
 
 
−
{| align="center" border="1" cellpadding="4" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:90%"
 
−
|+ '''Table 1. Propositional Forms on Two Variables'''
 
−
|- style="background:paleturquoise"
 
−
! style="width:15%" | L<sub>1</sub>
 
−
! style="width:15%" | L<sub>2</sub>
 
−
! style="width:15%" | L<sub>3</sub>
 
−
! style="width:15%" | L<sub>4</sub>
 
−
! style="width:15%" | L<sub>5</sub>
 
−
! style="width:15%" | L<sub>6</sub>
 
−
|- style="background:paleturquoise"
 
−
| &nbsp;
 
−
| align="right" | x :
 
−
| 1 1 0 0
 
−
| &nbsp;
 
−
| &nbsp;
 
−
| &nbsp;
 
−
|- style="background:paleturquoise"
 
−
| &nbsp;
 
−
| align="right" | y :
 
−
| 1 0 1 0
 
−
| &nbsp;
 
 
| &nbsp;
 
| &nbsp;
 +
| align="right" | <math>x\colon\!</math>
 +
| <math>1~1~0~0\!</math>
 +
| &nbsp; || &nbsp; || &nbsp;
 +
|- style="background:ghostwhite"
 
| &nbsp;
 
| &nbsp;
 +
| align="right" | <math>y\colon\!</math>
 +
| <math>1~0~1~0\!</math>
 +
| &nbsp; || &nbsp; || &nbsp;
 
|-
 
|-
−
| f<sub>0</sub> || f<sub>0000</sub> || 0 0 0 0 || (&nbsp;) || false || 0
+
| <math>f_{0}\!</math>
 +
| <math>f_{0000}\!</math>
 +
| <math>0~0~0~0</math>
 +
| <math>\texttt{(~)}\!</math>
 +
| <math>\text{false}\!</math>
 +
| <math>0\!</math>
 
|-
 
|-
−
| f<sub>1</sub> || f<sub>0001</sub> || 0 0 0 1 || (x)(y) || neither x nor y || &not;x &and; &not;y
+
|
 +
<math>\begin{matrix}
 +
f_{1}\\f_{2}\\f_{4}\\f_{8}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
f_{0001}\\f_{0010}\\f_{0100}\\f_{1000}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
0~0~0~1\\0~0~1~0\\0~1~0~0\\1~0~0~0
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~~} y \texttt{~}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{neither}~ x ~\text{nor}~ y
 +
\\
 +
y ~\text{without}~ x
 +
\\
 +
x ~\text{without}~ y
 +
\\
 +
x ~\text{and}~ y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\lnot x \land \lnot y
 +
\\
 +
\lnot x \land y
 +
\\
 +
x \land \lnot y
 +
\\
 +
x \land y
 +
\end{matrix}</math>
 
|-
 
|-
−
| f<sub>2</sub> || f<sub>0010</sub> || 0 0 1 0 || (x) y || y and not x || &not;x &and; y
+
|
 +
<math>\begin{matrix}
 +
f_{3}\\f_{12}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
f_{0011}\\f_{1100}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
0~0~1~1\\1~1~0~0
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{not}~ x
 +
\\
 +
x
 +
\end{matrix}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
\lnot x
 +
\\
 +
x
 +
\end{matrix}</math>
 
|-
 
|-
−
| f<sub>3</sub> || f<sub>0011</sub> || 0 0 1 1 || (x) || not x || &not;x
+
|
 +
<math>\begin{matrix}
 +
f_{6}\\f_{9}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
f_{0110}\\f_{1001}
 +
\end{matrix}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
0~1~1~0\\1~0~0~1
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
x ~\text{not equal to}~ y
 +
\\
 +
x ~\text{equal to}~ y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
x \ne y
 +
\\
 +
x = y
 +
\end{matrix}</math>
 
|-
 
|-
−
| f<sub>4</sub> || f<sub>0100</sub> || 0 1 0 0 || x (y) || x and not y || x &and; &not;y
+
|
 +
<math>\begin{matrix}
 +
f_{5}\\f_{10}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
f_{0101}\\f_{1010}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
0~1~0~1\\1~0~1~0
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{not}~ y
 +
\\
 +
y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\lnot y
 +
\\
 +
y
 +
\end{matrix}</math>
 
|-
 
|-
−
| f<sub>5</sub> || f<sub>0101</sub> || 0 1 0 1 || (y) || not y || &not;y
+
|
 +
<math>\begin{matrix}
 +
f_{7}\\f_{11}\\f_{13}\\f_{14}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
f_{0111}\\f_{1011}\\f_{1101}\\f_{1110}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
0~1~1~1\\1~0~1~1\\1~1~0~1\\1~1~1~0
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\texttt{~(} x \texttt{~~} y \texttt{)~}
 +
\\
 +
\texttt{~(} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\text{not both}~ x ~\text{and}~ y
 +
\\
 +
\text{not}~ x ~\text{without}~ y
 +
\\
 +
\text{not}~ y ~\text{without}~ x
 +
\\
 +
x ~\text{or}~ y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\lnot x \lor \lnot y
 +
\\
 +
x \Rightarrow y
 +
\\
 +
x \Leftarrow y
 +
\\
 +
x \lor y
 +
\end{matrix}</math>
 
|-
 
|-
−
| f<sub>6</sub> || f<sub>0110</sub> || 0 1 1 0 || (x, y) || x not equal to y || x &ne; y
+
| <math>f_{15}\!</math>
−
|-
+
| <math>f_{1111}\!</math>
−
| f<sub>7</sub> || f<sub>0111</sub> || 0 1 1 1 || (x&nbsp;y) || not both x and y || &not;x &or; &not;y
+
| <math>1~1~1~1\!</math>
−
|-
+
| <math>\texttt{((~))}\!</math>
−
| f<sub>8</sub> || f<sub>1000</sub> || 1 0 0 0 || x&nbsp;y || x and y || x &and; y
+
| <math>\text{true}\!</math>
 +
| <math>1\!</math>
 +
|}
 +
 
 +
<br>
 +
 
 +
====Table A3. E''f'' Expanded Over Differential Features====
 +
 
 +
<br>
 +
 
 +
{| align="center" cellpadding="6" cellspacing="0" style="border-bottom:1px solid black; border-left:1px solid black; border-right:1px solid black; border-top:1px solid black; text-align:center; width:80%"
 +
|+ style="height:30px" | <math>\text{Table A3.} ~~ \mathrm{E}f ~\text{Expanded Over Differential Features}~ \{ \mathrm{d}x, \mathrm{d}y \}\!</math>
 +
|- style="background:ghostwhite"
 +
| style="width:10%; border-bottom:1px solid black" | &nbsp;
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" | <math>f\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}\mathrm{T}_{11}f\\\mathrm{E}f|_{\mathrm{d}x ~ \mathrm{d}y}\end{matrix}</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}\mathrm{T}_{10}f\\\mathrm{E}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}}\end{matrix}</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}\mathrm{T}_{01}f\\\mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y}\end{matrix}</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}\mathrm{T}_{00}f\\\mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}}\end{matrix}</math>
 
|-
 
|-
−
| f<sub>9</sub> || f<sub>1001</sub> || 1 0 0 1 || ((x, y)) || x equal to y || x = y
+
| style="border-top:1px solid black" | <math>f_{0}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 
|-
 
|-
−
| f<sub>10</sub> || f<sub>1010</sub> || 1 0 1 0 || y || y || y
+
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
f_{1}\\f_{2}\\f_{4}\\f_{8}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~} x \texttt{~~} y \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\\
 +
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~~} y \texttt{~}
 +
\\
 +
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\end{matrix}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\\
 +
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~~} y \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~~} y \texttt{~}
 +
\end{matrix}</math>
 
|-
 
|-
−
| f<sub>11</sub> || f<sub>1011</sub> || 1 0 1 1 || (x (y)) || not x without y || x &rarr; y
+
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
f_{3}\\f_{12}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~} x \texttt{~}
 +
\\
 +
\texttt{(} x \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~} x \texttt{~}
 +
\\
 +
\texttt{(} x \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~}
 +
\end{matrix}</math>
 
|-
 
|-
−
| f<sub>12</sub> || f<sub>1100</sub> || 1 1 0 0 || x || x || x
+
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
f_{6}\\f_{9}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\\
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\\
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 
|-
 
|-
−
| f<sub>13</sub> || f<sub>1101</sub> || 1 1 0 1 || ((x) y) || not y without x || x &larr; y
+
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
f_{5}\\f_{10}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~} y \texttt{~}
 +
\\
 +
\texttt{(} y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~} y \texttt{~}
 +
\\
 +
\texttt{(} y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\end{matrix}</math>
 
|-
 
|-
−
| f<sub>14</sub> || f<sub>1110</sub> || 1 1 1 0 || ((x)(y)) || x or y || x &or; y
+
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
f_{7}\\f_{11}\\f_{13}\\f_{14}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(~} x \texttt{~~} y \texttt{~)}
 +
\\
 +
\texttt{(~} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{~)}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{~)}
 +
\\
 +
\texttt{(~} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{(~} x \texttt{~~} y \texttt{~)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{((} x \texttt{)~} y \texttt{~)}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\\
 +
\texttt{(~} x \texttt{~~} y \texttt{~)}
 +
\\
 +
\texttt{(~} x \texttt{~(} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(~} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{(~} x \texttt{~~} y \texttt{~)}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{~)}
 +
\end{matrix}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(~} x \texttt{~~} y \texttt{~)}
 +
\\
 +
\texttt{(~} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{~)}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\end{matrix}</math>
 
|-
 
|-
−
| f<sub>15</sub> || f<sub>1111</sub> || 1 1 1 1 || ((&nbsp;)) || true || 1
+
| style="border-top:1px solid black" | <math>f_{15}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>1\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" | <math>1\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>1\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>1\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>1\!</math>
 +
|- style="background:ghostwhite"
 +
| style="border-top:1px solid black" colspan="2" | <math>\text{Fixed Point Total}\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" | <math>4\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>4\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>4\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>16\!</math>
 
|}
 
|}
 +
 
<br>
 
<br>
  
−
The next four Tables expand the expressions of ''Ef'' and ''Df'' in two different ways, for each of the sixteen functions.  Notice that the functions are given in a different order, here being collected into a set of seven natural classes.
+
====Table A4. D''f'' Expanded Over Differential Features====
  
−
<pre>
+
<br>
−
Table 2.  Ef Expanded Over Ordinary Features {x, y}
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
|      |    f      |  Ef | xy  | Ef | x(y)  | Ef | (x)y  | Ef | (x)(y)|
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_0  |    ()    |    ()    |    ()    |    ()    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_1  |  (x)(y)  |  dx  dy  |  dx (dy)  |  (dx) dy  |  (dx)(dy)  |
 
−
|      |            |            |            |            |            |
 
−
| f_2  |  (x) y    |  dx (dy)  |  dx  dy  |  (dx)(dy)  |  (dx) dy  |
 
−
|      |            |            |            |            |            |
 
−
| f_4  |    x (y)  |  (dx) dy  |  (dx)(dy)  |  dx  dy  |  dx (dy)  |
 
−
|      |            |            |            |            |            |
 
−
| f_8  |    x  y    |  (dx)(dy)  |  (dx) dy  |  dx (dy)  |  dx  dy  |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_3  |  (x)      |  dx      |  dx      |  (dx)      |  (dx)      |
 
−
|      |            |            |            |            |            |
 
−
| f_12 |    x      |  (dx)      |  (dx)      |  dx      |  dx      |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_6  |  (x, y)  |  (dx, dy)  | ((dx, dy)) | ((dx, dy)) |  (dx, dy)  |
 
−
|      |            |            |            |            |            |
 
−
| f_9  |  ((x, y))  | ((dx, dy)) |  (dx, dy)  |  (dx, dy)  | ((dx, dy)) |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_5  |      (y)  |      dy  |      (dy)  |      dy  |      (dy)  |
 
−
|      |            |            |            |            |            |
 
−
| f_10 |      y    |      (dy)  |      dy  |      (dy)  |      dy  |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_7  |  (x  y)  | ((dx)(dy)) | ((dx) dy)  |  (dx (dy)) |  (dx  dy)  |
 
−
|      |            |            |            |            |            |
 
−
| f_11 |  (x (y))  | ((dx) dy)  | ((dx)(dy)) |  (dx  dy)  |  (dx (dy)) |
 
−
|      |            |            |            |            |            |
 
−
| f_13 |  ((x) y)  |  (dx (dy)) |  (dx  dy)  | ((dx)(dy)) | ((dx) dy)  |
 
−
|      |            |            |            |            |            |
 
−
| f_14 |  ((x)(y))  |  (dx  dy)  |  (dx (dy)) | ((dx) dy)  | ((dx)(dy)) |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_15 |    (())    |    (())    |    (())    |    (())    |    (())    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
</pre>
 
−
<pre>
 
−
Table 3.  Df Expanded Over Ordinary Features {x, y}
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
|      |    f      |  Df | xy  | Df | x(y)  | Df | (x)y  | Df | (x)(y)|
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_0  |    ()    |    ()    |    ()    |    ()    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_1  |  (x)(y)  |  dx  dy  |  dx (dy)  |  (dx) dy  | ((dx)(dy)) |
 
−
|      |            |            |            |            |            |
 
−
| f_2  |  (x) y    |  dx (dy)  |  dx  dy  | ((dx)(dy)) |  (dx) dy  |
 
−
|      |            |            |            |            |            |
 
−
| f_4  |    x (y)  |  (dx) dy  | ((dx)(dy)) |  dx  dy  |  dx (dy)  |
 
−
|      |            |            |            |            |            |
 
−
| f_8  |    x  y    | ((dx)(dy)) |  (dx) dy  |  dx (dy)  |  dx  dy  |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_3  |  (x)      |  dx      |  dx      |  dx      |  dx      |
 
−
|      |            |            |            |            |            |
 
−
| f_12 |    x      |  dx      |  dx      |  dx      |  dx      |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_6  |  (x, y)  |  (dx, dy)  |  (dx, dy)  |  (dx, dy)  |  (dx, dy)  |
 
−
|      |            |            |            |            |            |
 
−
| f_9  |  ((x, y))  |  (dx, dy)  |  (dx, dy)  |  (dx, dy)  |  (dx, dy)  |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_5  |      (y)  |      dy  |      dy  |      dy  |      dy  |
 
−
|      |            |            |            |            |            |
 
−
| f_10 |      y    |      dy  |      dy  |      dy  |      dy  |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_7  |  (x  y)  | ((dx)(dy)) |  (dx) dy  |  dx (dy)  |  dx  dy  |
 
−
|      |            |            |            |            |            |
 
−
| f_11 |  (x (y))  |  (dx) dy  | ((dx)(dy)) |  dx  dy  |  dx (dy)  |
 
−
|      |            |            |            |            |            |
 
−
| f_13 |  ((x) y)  |  dx (dy)  |  dx  dy  | ((dx)(dy)) |  (dx) dy  |
 
−
|      |            |            |            |            |            |
 
−
| f_14 |  ((x)(y))  |  dx  dy  |  dx (dy)  |  (dx) dy  | ((dx)(dy)) |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_15 |    (())    |    ()    |    ()    |    ()    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
</pre>
 
−
<pre>
 
−
Table 4.  Ef Expanded Over Differential Features {dx, dy}
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
|      |    f      |  T_11 f  |  T_10 f  |  T_01 f  |  T_00 f  |
 
−
|      |            |            |            |            |            |
 
−
|      |            | Ef| dx dy  | Ef| dx(dy) | Ef| (dx)dy | Ef|(dx)(dy)|
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_0  |    ()    |    ()    |    ()    |    ()    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_1  |  (x)(y)  |    x  y    |    x (y)  |  (x) y    |  (x)(y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_2  |  (x) y    |    x (y)  |    x  y    |  (x)(y)  |  (x) y    |
 
−
|      |            |            |            |            |            |
 
−
| f_4  |    x (y)  |  (x) y    |  (x)(y)  |    x  y    |    x (y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_8  |    x  y    |  (x)(y)  |  (x) y    |    x (y)  |    x  y    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_3  |  (x)      |    x      |    x      |  (x)      |  (x)      |
 
−
|      |            |            |            |            |            |
 
−
| f_12 |    x      |  (x)      |  (x)      |    x      |    x      |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_6  |  (x, y)  |  (x, y)  |  ((x, y))  |  ((x, y))  |  (x, y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_9  |  ((x, y))  |  ((x, y))  |  (x, y)  |  (x, y)  |  ((x, y))  |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_5  |      (y)  |      y    |      (y)  |      y    |      (y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_10 |      y    |      (y)  |      y    |      (y)  |      y    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_7  |  (x  y)  |  ((x)(y))  |  ((x) y)  |  (x (y))  |  (x  y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_11 |  (x (y))  |  ((x) y)  |  ((x)(y))  |  (x  y)  |  (x (y))  |
 
−
|      |            |            |            |            |            |
 
−
| f_13 |  ((x) y)  |  (x (y))  |  (x  y)  |  ((x)(y))  |  ((x) y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_14 |  ((x)(y))  |  (x  y)  |  (x (y))  |  ((x) y)  |  ((x)(y))  |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_15 |    (())    |    (())    |    (())    |    (())    |    (())    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|                  |            |            |            |            |
 
−
| Fixed Point Total |      4    |      4    |      4    |    16    |
 
−
|                  |            |            |            |            |
 
−
o-------------------o------------o------------o------------o------------o
 
−
</pre>
 
−
<pre>
 
−
Table 5.  Df Expanded Over Differential Features {dx, dy}
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
|      |    f      | Df| dx dy  | Df| dx(dy) | Df| (dx)dy | Df|(dx)(dy)|
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_0  |    ()    |    ()    |    ()    |    ()    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_1  |  (x)(y)  |  ((x, y))  |    (y)    |    (x)    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
| f_2  |  (x) y    |  (x, y)  |    y      |    (x)    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
| f_4  |    x (y)  |  (x, y)  |    (y)    |    x      |    ()    |
 
−
|      |            |            |            |            |            |
 
−
| f_8  |    x  y    |  ((x, y))  |    y      |    x      |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_3  |  (x)      |    (())    |    (())    |    ()    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
| f_12 |    x      |    (())    |    (())    |    ()    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_6  |  (x, y)  |    ()    |    (())    |    (())    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
| f_9  |  ((x, y))  |    ()    |    (())    |    (())    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_5  |      (y)  |    (())    |    ()    |    (())    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
| f_10 |      y    |    (())    |    ()    |    (())    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_7  |  (x  y)  |  ((x, y))  |    y      |    x      |    ()    |
 
−
|      |            |            |            |            |            |
 
−
| f_11 |  (x (y))  |  (x, y)  |    (y)    |    x      |    ()    |
 
−
|      |            |            |            |            |            |
 
−
| f_13 |  ((x) y)  |  (x, y)  |    y      |    (x)    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
| f_14 |  ((x)(y))  |  ((x, y))  |    (y)    |    (x)    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_15 |    (())    |    ()    |    ()    |    ()    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
</pre>
 
  
−
If the medium truly is the message, the blank slate is the innate idea.
+
{| align="center" cellpadding="6" cellspacing="0" style="border-bottom:1px solid black; border-left:1px solid black; border-right:1px solid black; border-top:1px solid black; text-align:center; width:80%"
 +
|+ style="height:30px" | <math>\text{Table A4.} ~~ \mathrm{D}f ~\text{Expanded Over Differential Features}~ \{ \mathrm{d}x, \mathrm{d}y \}\!</math>
 +
|- style="background:ghostwhite"
 +
| style="width:10%; border-bottom:1px solid black" | &nbsp;
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" | <math>f\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:4px double black" |
 +
<math>\mathrm{D}f|_{\mathrm{d}x ~ \mathrm{d}y}\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\mathrm{D}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}}\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y}~\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}}\!</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{0}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
|-
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
f_{1}\\f_{2}\\f_{4}\\f_{8}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\\
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
y
 +
\\
 +
\texttt{(} y \texttt{)}
 +
\\
 +
y
 +
\end{matrix}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)}
 +
\\
 +
x
 +
\\
 +
x
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}0\\0\\0\\0\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}f_{3}\\f_{12}\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)}
 +
\\
 +
x
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}1\\1\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}1\\1\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}0\\0\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}0\\0\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}f_{6}\\f_{9}\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}0\\0\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}1\\1\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}1\\1\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}0\\0\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}f_{5}\\f_{10}\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}1\\1\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}0\\0\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}1\\1\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}0\\0\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(~} x \texttt{~~} y \texttt{~)}
 +
\\
 +
\texttt{(~} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{~)}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\\
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
y
 +
\\
 +
\texttt{(} y \texttt{)}
 +
\\
 +
y
 +
\\
 +
\texttt{(} y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
x
 +
\\
 +
x
 +
\\
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}0\\0\\0\\0\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{15}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>1\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
|}
  
−
===Note 7===
+
<br>
  
−
If you think that I linger in the realm of logical difference calculus out of sheer vacillation about getting down to the differential proper, it is probably out of a prior expectation that you derive from the art or the long-engrained practice of real analysis. But the fact is that ordinary calculus only rushes on to the sundry orders of approximation because the strain of comprehending the full import of ''E'' and ''D'' at once whelm over its discrete and finite powers to grasp them.  But here, in the fully serene idylls of ZOL, we find ourselves fit with the compass of a wit that is all we'd ever wish to explore their effects with care.
+
====Table A5. E''f'' Expanded Over Ordinary Features====
  
−
So let us do just that.
+
<br>
  
−
I will first rationalize the novel grouping of propositional forms in the last set of Tables, as that will extend a gentle invitation to the mathematical subject of group theory, and demonstrate its relevance to differential logic in a strikingly apt and useful way. The data for that account is contained in Table 4.
+
{| align="center" cellpadding="6" cellspacing="0" style="border-bottom:1px solid black; border-left:1px solid black; border-right:1px solid black; border-top:1px solid black; text-align:center; width:80%"
 +
|+ style="height:30px" | <math>\text{Table A5.} ~~ \mathrm{E}f ~\text{Expanded Over Ordinary Features}~ \{ x, y \}\!</math>
 +
|- style="background:ghostwhite"
 +
| style="width:10%; border-bottom:1px solid black" | &nbsp;
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" | <math>f\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:4px double black" |
 +
<math>\mathrm{E}f|_{xy}\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\mathrm{E}f|_{x \texttt{(} y \texttt{)}}\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\mathrm{E}f|_{\texttt{(} x \texttt{)} y}\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\mathrm{E}f|_{\texttt{(} x \texttt{)(} y \texttt{)}}\!</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{0}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
|-
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
f_{1}\\f_{2}\\f_{4}\\f_{8}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\end{matrix}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
f_{3}\\f_{12}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~} \mathrm{d}x \texttt{~}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~} \mathrm{d}x \texttt{~}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}x \texttt{)}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}x \texttt{)}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~}
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
f_{6}\\f_{9}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))}
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
f_{5}\\f_{10}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{(} \mathrm{d}y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{~} \mathrm{d}y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{(} \mathrm{d}y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{~} \mathrm{d}y \texttt{~}
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
f_{7}\\f_{11}\\f_{13}\\f_{14}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(~} x \texttt{~~} y \texttt{~)}
 +
\\
 +
\texttt{(~} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{~)}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)}
 +
\\
 +
\texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)}
 +
\\
 +
\texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)}
 +
\end{matrix}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)}
 +
\\
 +
\texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{15}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>1\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" | <math>1\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>1\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>1\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" | <math>1\!</math>
 +
|}
  
−
<pre>
+
<br>
−
Table 4.  Ef Expanded Over Differential Features {dx, dy}
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
|      |    f      |  T_11 f  |  T_10 f  |  T_01 f  |  T_00 f  |
 
−
|      |            |            |            |            |            |
 
−
|      |            | Ef| dx dy  | Ef| dx(dy) | Ef| (dx)dy | Ef|(dx)(dy)|
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_0  |    ()    |    ()    |    ()    |    ()    |    ()    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_1  |  (x)(y)  |    x  y    |    x (y)  |  (x) y    |  (x)(y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_2  |  (x) y    |    x (y)  |    x  y    |  (x)(y)  |  (x) y    |
 
−
|      |            |            |            |            |            |
 
−
| f_4  |    x (y)  |  (x) y    |  (x)(y)  |    x  y    |    x (y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_8  |    x  y    |  (x)(y)  |  (x) y    |    x (y)  |    x  y    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_3  |  (x)      |    x      |    x      |  (x)      |  (x)      |
 
−
|      |            |            |            |            |            |
 
−
| f_12 |    x      |  (x)      |  (x)      |    x      |    x      |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_6  |  (x, y)  |  (x, y)  |  ((x, y))  |  ((x, y))  |  (x, y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_9  |  ((x, y))  |  ((x, y))  |  (x, y)  |  (x, y)  |  ((x, y))  |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_5  |      (y)  |      y    |      (y)  |      y    |      (y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_10 |      y    |      (y)  |      y    |      (y)  |      y    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_7  |  (x  y)  |  ((x)(y))  |  ((x) y)  |  (x (y))  |  (x  y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_11 |  (x (y))  |  ((x) y)  |  ((x)(y))  |  (x  y)  |  (x (y))  |
 
−
|      |            |            |            |            |            |
 
−
| f_13 |  ((x) y)  |  (x (y))  |  (x  y)  |  ((x)(y))  |  ((x) y)  |
 
−
|      |            |            |            |            |            |
 
−
| f_14 |  ((x)(y))  |  (x  y)  |  (x (y))  |  ((x) y)  |  ((x)(y))  |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|      |            |            |            |            |            |
 
−
| f_15 |    (())    |    (())    |    (())    |    (())    |    (())    |
 
−
|      |            |            |            |            |            |
 
−
o------o------------o------------o------------o------------o------------o
 
−
|                  |            |            |            |            |
 
−
| Fixed Point Total |      4    |      4    |      4    |    16    |
 
−
|                  |            |            |            |            |
 
−
o-------------------o------------o------------o------------o------------o
 
−
</pre>
 
  
−
The shift operator ''E'' can be understood as enacting a substitution operation on the proposition that is given as its argument.  In our immediate example, we have the following data and definition:
+
====Table A6. D''f'' Expanded Over Ordinary Features====
  
−
: ''E'' : (''U'' &rarr; '''B''') &rarr; (''EU'' &rarr; '''B'''),
+
<br>
  
−
: ''E'' : ''f''(''x'', ''y'') &rarr; ''Ef''(''x'', ''y'', ''dx'', ''dy''),
+
{| align="center" cellpadding="6" cellspacing="0" style="border-bottom:1px solid black; border-left:1px solid black; border-right:1px solid black; border-top:1px solid black; text-align:center; width:80%"
 +
|+ style="height:30px" | <math>\text{Table A6.} ~~ \mathrm{D}f ~\text{Expanded Over Ordinary Features}~ \{ x, y \}\!</math>
 +
|- style="background:ghostwhite"
 +
| style="width:10%; border-bottom:1px solid black" | &nbsp;
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" | <math>f\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:4px double black" |
 +
<math>\mathrm{D}f|_{xy}\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\mathrm{D}f|_{x \texttt{(} y \texttt{)}}\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\mathrm{D}f|_{\texttt{(} x \texttt{)} y}\!</math>
 +
| style="width:18%; border-bottom:1px solid black; border-left:1px solid black" |
 +
<math>\mathrm{D}f|_{\texttt{(} x \texttt{)(} y \texttt{)}}\!</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{0}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\end{matrix}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>\begin{matrix}f_{3}\\f_{12}\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}\texttt{(} x \texttt{)}\\\texttt{~} x \texttt{~}\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>\begin{matrix}f_{6}\\f_{9}\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)}
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>\begin{matrix}f_{5}\\f_{10}\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(~} x \texttt{~~} y \texttt{~)}
 +
\\
 +
\texttt{(~} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{~)}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\end{matrix}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
\texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)}
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~}
 +
\\
 +
\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{15}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>1\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black"  | <math>0\!</math>
 +
|}
  
−
: ''Ef''(''x'', ''y'', ''dx'', ''dy'') = ''f''(''x'' + ''dx'', ''y'' + ''dy'').
+
<br>
  
−
Therefore, if we evaluate ''Ef'' at particular values of ''dx'' and ''dy'', for example, ''dx'' = ''i'' and ''dy'' = ''j'', where ''i'', ''j'' are in '''B''', we obtain:
+
===Appendix 2. Differential Forms===
  
−
: ''E''<sub>''ij''</sub> : (''U'' &rarr; ''B'') &rarr; (''U'' &rarr; '''B'''),
+
The actions of the difference operator <math>\mathrm{D}\!</math> and the tangent operator <math>\mathrm{d}\!</math> on the 16 bivariate propositions are shown in Tables&nbsp;A7 and A8.
  
−
: ''E''<sub>''ij''</sub> : f &rarr; : ''E''<sub>''ij''</sub>''f'',
+
Table A7 expands the differential forms that result over a ''logical basis'':
  
−
: ''E''<sub>''ij''</sub>f = ''Ef''|<''dx'' = ''i'', ''dy'' = ''j''> = ''f''(''x'' + ''i'', ''y'' + ''j'').
+
{| align="center" cellpadding="6" style="text-align:center"
 +
|
 +
<math>\{~ \texttt{(}\mathrm{d}x\texttt{)(}\mathrm{d}y\texttt{)}, ~\mathrm{d}x~\texttt{(}\mathrm{d}y\texttt{)}, ~\texttt{(}\mathrm{d}x\texttt{)}~\mathrm{d}y, ~\mathrm{d}x~\mathrm{d}y ~\}.\!</math>
 +
|}
  
−
The notation is a little bit awkward, but the data of the Table should make the sense clear.  The important thing to observe is that ''E''<sub>''ij''</sub> has the effect of transforming each proposition ''f''&nbsp;:&nbsp;''U''&nbsp;&rarr;&nbsp;'''B''' into some other proposition ''f''´&nbsp;:&nbsp;''U''&nbsp;&rarr;&nbsp;'''B'''.  As it happens, the action is one-to-one and onto for each ''E''<sub>''ij''</sub>, so the gang of four operators {''E''<sub>''ij''</sub> : ''i'', ''j'' in '''B'''} is an example of what is called a ''transformation group'' on the set of sixteen propositions.  Bowing to a longstanding local and linear tradition, I will therefore redub the four elements of this group as T<sub>00</sub>, T<sub>01</sub>, T<sub>10</sub>, T<sub>11</sub>, to bear in mind their transformative character, or nature, as the case may be.  Abstractly viewed, this group of order four has the following operation table:
+
This set consists of the singular propositions in the first order differential variables, indicating mutually exclusive and exhaustive ''cells'' of the tangent universe of discourse.  Accordingly, this set of differential propositions may also be referred to as the cell-basis, point-basis, or singular differential basis.  In this setting it is frequently convenient to use the following abbreviations:
  
−
<pre>
+
{| align="center" cellpadding="6" style="text-align:center"
−
o----------o----------o----------o----------o----------o
+
|
−
|         %          |          |          |          |
+
<math>\partial x ~=~ \mathrm{d}x~\texttt{(}\mathrm{d}y\texttt{)}\!</math> &nbsp; &nbsp; and &nbsp; &nbsp; <math>\partial y ~=~ \texttt{(}\mathrm{d}x\texttt{)}~\mathrm{d}y.\!</math>
−
|    *    %  T_00  |  T_01  |  T_10  |  T_11  |
+
|}
−
|          %          |          |          |          |
 
−
o==========o==========o==========o==========o==========o
 
−
|          %          |          |          |          |
 
−
|  T_00  %  T_00  |  T_01  |  T_10  |  T_11  |
 
−
|          %          |          |          |          |
 
−
o----------o----------o----------o----------o----------o
 
−
|          %          |          |          |          |
 
−
|  T_01  %  T_01  |  T_00  |  T_11  |  T_10  |
 
−
|          %          |          |          |          |
 
−
o----------o----------o----------o----------o----------o
 
−
|          %          |          |          |          |
 
−
|  T_10  %  T_10  |  T_11  |  T_00  |  T_01  |
 
−
|          %          |          |          |          |
 
−
o----------o----------o----------o----------o----------o
 
−
|          %          |          |          |          |
 
−
|  T_11  %  T_11  |  T_10  |  T_01  |  T_00  |
 
−
|          %          |          |          |          |
 
−
o----------o----------o----------o----------o----------o
 
−
</pre>
 
  
−
It happens that there are just two possible groups of 4 elements.  One is the cyclic group ''Z''<sub>4</sub> (German ''Zyklus''), which this is not.  The other is Klein's four-group ''V''<sub>4</sub> (German ''Vier''), which it is.
+
Table A8 expands the differential forms that result over an ''algebraic basis'':
  
−
More concretely viewed, the group as a whole pushes the set of sixteen propositions around in such a way that they fall into seven natural classes, called ''orbits''.  One says that the orbits are preserved by the action of the group.  There is an ''Orbit Lemma'' of immense utility to "those who count" which, depending on your upbringing, you may associate with the names of Burnside, Cauchy, Frobenius, or some subset or superset of these three, vouching that the number of orbits is equal to the mean number of fixed points, in other words, the total number of points (in our case, propositions) that are left unmoved by the separate operations, divided by the order of the group. In this instance, T<sub>00</sub> operates as the group identity, fixing all 16 propositions, while the other three group elements fix 4 propositions each, and so we get:
+
{| align="center" cellpadding="6" style="text-align:center"
 +
| <math>\{~ 1, ~\mathrm{d}x, ~\mathrm{d}y, ~\mathrm{d}x~\mathrm{d}y ~\}.\!</math>
 +
|}
  
−
: Number of orbits = (4 + 4 + 4 + 16) ÷ 4 = 7.
+
This set consists of the ''positive propositions'' in the first order differential variables, indicating overlapping positive regions of the tangent universe of discourse.  Accordingly, this set of differential propositions may also be referred to as the ''positive differential basis''.
  
−
Amazing!
+
====Table A7. Differential Forms Expanded on a Logical Basis====
  
−
===Note 8===
+
<br>
  
−
We have been contemplating functions of the type ''f''&nbsp;:&nbsp;''U''&nbsp;&rarr;&nbsp;'''B''', studying the action of the operators ''E'' and ''D'' on this family.  These functions, that we may identify for our present aims with propositions, inasmuch as they capture their abstract forms, are logical analogues of ''scalar potential fields''.  These are the sorts of fields that are so picturesquely presented in elementary calculus and physics textbooks by images of snow-covered hills and parties of skiers who trek down their slopes like least action heroes.  The analogous scene in propositional logic presents us with forms more reminiscent of plateaunic idylls, being all plains at one of two levels, the mesas of verity and falsity, as it were, with nary a niche to inhabit between them, restricting our options for a sporting gradient of downhill dynamics to just one of two, standing still on level ground or falling off a bluff.
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:center; width:90%"
 +
|+ style="height:30px" | <math>\text{Table A7.} ~~ \text{Differential Forms Expanded on a Logical Basis}\!</math>
 +
|- style="background:ghostwhite; height:40px"
 +
| &nbsp;
 +
| style="border-right:none" | <math>f\!</math>
 +
| style="border-left:4px double black" | <math>\mathrm{D}f~\!</math>
 +
| <math>\mathrm{d}f~\!</math>
 +
|-
 +
| <math>f_{0}\!</math>
 +
| style="border-right:none" | <math>\texttt{(~)}\!</math>
 +
| style="border-left:4px double black" | <math>0\!</math>
 +
| <math>0\!</math>
 +
|-
 +
| <math>\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}</math>
 +
| style="border-right:none" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)}
 +
& + &
 +
\texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y
 +
& + &
 +
\texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y
 +
\\
 +
y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)}
 +
& + &
 +
\texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y
 +
& + &
 +
\texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)}
 +
& + &
 +
x & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y
 +
& + &
 +
\texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y
 +
\\
 +
y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)}
 +
& + &
 +
x & \texttt{(} \mathrm{d}x) ~ \mathrm{d}y
 +
& + &
 +
\texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)} ~\partial x
 +
& + &
 +
\texttt{(} x \texttt{)} ~\partial y
 +
\\
 +
\texttt{~} y \texttt{~} ~\partial x
 +
& + &
 +
\texttt{(} x \texttt{)} ~\partial y
 +
\\
 +
\texttt{(} y \texttt{)} ~\partial x
 +
& + &
 +
\texttt{~} x \texttt{~} ~\partial y
 +
\\
 +
\texttt{~} y \texttt{~} ~\partial x
 +
& + &
 +
\texttt{~} x \texttt{~} ~\partial y
 +
\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{3}\\f_{12}\end{matrix}</math>
 +
| style="border-right:none" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \mathrm{d}x ~ \mathrm{d}y
 +
\\
 +
\mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \mathrm{d}x ~ \mathrm{d}y
 +
\end{matrix}\!</math>
 +
|
 +
<math>\begin{matrix}
 +
\partial x
 +
\\
 +
\partial x
 +
\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{6}\\f_{9}\end{matrix}</math>
 +
| style="border-right:none" |
 +
<math>\begin{matrix}
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y
 +
\\
 +
\mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\partial x & + & \partial y
 +
\\
 +
\partial x & + & \partial y
 +
\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{5}\\f_{10}\end{matrix}</math>
 +
| style="border-right:none" |
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \mathrm{d}x ~ \mathrm{d}y
 +
\\
 +
\texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \mathrm{d}x ~ \mathrm{d}y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\partial y
 +
\\
 +
\partial y
 +
\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}</math>
 +
| style="border-right:none" |
 +
<math>\begin{matrix}
 +
\texttt{(~} x \texttt{~~} y \texttt{~)}
 +
\\
 +
\texttt{(~} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{~)}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)}
 +
& + &
 +
x & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y
 +
& + &
 +
\texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)}
 +
& + &
 +
x & \texttt{(} \mathrm{d}x) ~ \mathrm{d}y
 +
& + &
 +
\texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y
 +
\\
 +
y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)}
 +
& + &
 +
\texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y
 +
& + &
 +
\texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)}
 +
& + &
 +
\texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y
 +
& + &
 +
\texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\texttt{~} y \texttt{~} ~\partial x
 +
& + &
 +
\texttt{~} x \texttt{~} ~\partial y
 +
\\
 +
\texttt{(} y \texttt{)} ~\partial x
 +
& + &
 +
\texttt{~} x \texttt{~} ~\partial y
 +
\\
 +
\texttt{~} y \texttt{~} ~\partial x
 +
& + &
 +
\texttt{(} x \texttt{)} ~\partial y
 +
\\
 +
\texttt{(} y \texttt{)} ~\partial x
 +
& + &
 +
\texttt{(} x \texttt{)} ~\partial y
 +
\end{matrix}</math>
 +
|-
 +
| <math>f_{15}\!</math>
 +
| style="border-right:none" | <math>\texttt{((~))}\!</math>
 +
| style="border-left:4px double black" | <math>0\!</math>
 +
| <math>0\!</math>
 +
|}
  
−
We are still working well within the logical analogue of the classical finite difference calculus, taking in the novelties that the logical transmutation of familiar elements is able to bring to light.  Soon we will take up several different notions of approximation relationships that may be seen to organize the space of propositions, and these will allow us to define several different forms of differential analysis applying to propositions.  In time we will find reason to consider more general types of maps, having concrete types of the form ''X''<sub>1</sub>&nbsp;&times;&nbsp;&hellip;&nbsp;&times;&nbsp;''X''<sub>''k''</sub>&nbsp;&rarr;&nbsp;''Y''<sub>1</sub>&nbsp;&times;&nbsp;&hellip;&nbsp;&times;&nbsp;''Y''<sub>''n''</sub> and abstract types '''B'''<sup>''k''</sup>&nbsp;&rarr;&nbsp;'''B'''<sup>''n''</sup>.  We will think of these mappings as transforming universes of discourse into themselves or into others, in short, as ''transformations of discourse''.
+
<br>
  
−
Before we continue with this intinerary, however, I would like to highlight another sort of ''differential aspect'' that concerns the ''boundary operator'' or the ''marked connective'' that serves as one of the two basic connectives in the cactus language for ZOL.
+
====Table A8. Differential Forms Expanded on an Algebraic Basis====
  
−
For example, consider the proposition ''f'' of concrete type ''f''&nbsp;:&nbsp;''X''&nbsp;&times;&nbsp;''Y''&nbsp;&times;&nbsp;''Z''&nbsp;&rarr;&nbsp;'''B''' and abstract type ''f''&nbsp;:&nbsp;'''B'''<sup>3</sup>&nbsp;&rarr;&nbsp;'''B''' that is written <code>(x, y, z)</code> in cactus syntax.  Taken as an assertion in what Peirce called the ''existential interpretation'', <code>(x, y, z)</code> says that just one of ''x'', ''y'', ''z'' is false.  It is useful to consider this assertion in relation to the conjunction ''xyz'' of the features that are engaged as its arguments.  A venn diagram of <code>(x, y, z)</code> looks like this:
+
<br>
  
−
<pre>
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:center; width:90%"
−
o-----------------------------------------------------------o
+
|+ style="height:30px" | <math>\text{Table A8.} ~~ \text{Differential Forms Expanded on an Algebraic Basis}\!</math>
−
| U                                                        |
+
|- style="background:ghostwhite; height:40px"
−
|                                                           |
+
| &nbsp;
−
|                     o-------------o                      |
+
| style="border-right:none" | <math>f\!</math>
−
|                     /               \                    |
+
| style="border-left:4px double black" | <math>\mathrm{D}f~\!</math>
−
|                   /                 \                   |
+
| <math>\mathrm{d}f~\!</math>
−
|                   /                   \                  |
+
|-
−
|                 /                     \                 |
+
| <math>f_{0}\!</math>
−
|                /                      \                 |
+
| style="border-right:none" | <math>\texttt{(~)}\!</math>
−
|                o            x           o                |
+
| style="border-left:4px double black" | <math>0\!</math>
−
|               |                         |               |
+
| <math>0\!</math>
−
|               |                         |                |
+
|-
−
|               |                         |               |
+
| <math>\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}</math>
−
|               |                         |                |
+
| style="border-right:none" |
−
|                |                        |                |
+
<math>\begin{matrix}
−
|             o--o----------o  o----------o--o            |
+
\texttt{(} x \texttt{)(} y \texttt{)}
−
|            /    \%%%%%%%%%%\ /%%%%%%%%%%/    \           |
+
\\
−
|          /      \%%%%%%%%%%o%%%%%%%%%%/     \           |
+
\texttt{(} x \texttt{)~} y \texttt{~}
−
|          /        \%%%%%%%%/ \%%%%%%%%/        \         |
+
\\
−
|        /          \%%%%%%/  \%%%%%%/         \        |
+
\texttt{~} x \texttt{~(} y \texttt{)}
−
|       /            \%%%%/    \%%%%/           \        |
+
\\
−
|       o              o--o-------o--o              o      |
+
\texttt{~} x \texttt{~~} y \texttt{~}
−
|       |                |%%%%%%%|                |      |
+
\end{matrix}</math>
−
|      |                |%%%%%%%|                |      |
+
| style="border-left:4px double black" |
−
|      |                |%%%%%%%|                |      |
+
<math>\begin{matrix}
−
|      |                |%%%%%%%|                |      |
+
\texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y
−
|      |                |%%%%%%%|                |      |
+
\\
−
|      o        y       o%%%%%%%o        z        o      |
+
\texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y
−
|        \                 \%%%%%/                 /        |
+
\\
−
|         \                 \%%%/                 /        |
+
\texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y
−
|          \                 \%/                 /          |
+
\\
−
|          \                 o                /           |
+
\texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y
−
|            \               / \               /           |
+
\end{matrix}</math>
−
|             o-------------o  o-------------o            |
+
|
−
|                                                           |
+
<math>\begin{matrix}
−
|                                                           |
+
\texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y
−
o-----------------------------------------------------------o
+
\\
−
</pre>
+
\texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y
 +
\\
 +
\texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y
 +
\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{3}\\f_{12}\end{matrix}</math>
 +
| style="border-right:none" |
 +
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\mathrm{d}x
 +
\\
 +
\mathrm{d}x
 +
\end{matrix}\!</math>
 +
| <math>\begin{matrix}
 +
\mathrm{d}x
 +
\\
 +
\mathrm{d}x
 +
\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{6}\\f_{9}\end{matrix}</math>
 +
| style="border-right:none" |
 +
<math>\begin{matrix}
 +
\texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\mathrm{d}x & + & \mathrm{d}y
 +
\\
 +
\mathrm{d}x & + & \mathrm{d}y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\mathrm{d}x & + & \mathrm{d}y
 +
\\
 +
\mathrm{d}x & + & \mathrm{d}y
 +
\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{5}\\f_{10}\end{matrix}</math>
 +
| style="border-right:none" |
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\mathrm{d}y
 +
\\
 +
\mathrm{d}y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\mathrm{d}y
 +
\\
 +
\mathrm{d}y
 +
\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}</math>
 +
| style="border-right:none" |
 +
<math>\begin{matrix}
 +
\texttt{(~} x \texttt{~~} y \texttt{~)}
 +
\\
 +
\texttt{(~} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{~)}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y
 +
\\
 +
\texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y
 +
\\
 +
\texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y
 +
\end{matrix}</math>
 +
|-
 +
| <math>f_{15}\!</math>
 +
| style="border-right:none" | <math>\texttt{((~))}\!</math>
 +
| style="border-left:4px double black" | <math>0\!</math>
 +
| <math>0\!</math>
 +
|}
  
−
In relation to the center cell indicated by the conjunction ''xyz'', the region indicated by <code>(x, y, z)</code> is comprised of the adjacent or the bordering cells.  Thus they are the cells that are just across the boundary of the center cell, as if reached by way of Leibniz's ''minimal changes'' from the point of origin, here, ''xyz''.
+
<br>
  
−
The same form of boundary relationship is exhibited for any cell of origin that one might elect to indicate, say, by means of the conjunction of positive and negative basis features ''u''<sub>1</sub>&nbsp;&hellip;&nbsp;''u''<sub>''k''</sub>, where ''u''<sub>''j''</sub> = ''x''<sub>''j''</sub> or ''u''<sub>''j''</sub> = (''x''<sub>''j''</sub>), for ''j'' = 1 to ''k''.  The proposition (''u''<sub>1</sub>,&nbsp;&hellip;,&nbsp;''u''<sub>''k''</sub>) indicates the disjunctive region consisting of the cells that are "just next door" to the cell ''u''<sub>1</sub>&nbsp;&hellip;&nbsp;''u''<sub>''k''</sub>.
+
====Table A9. Tangent Proposition as Pointwise Linear Approximation====
  
−
===Note 9===
+
<br>
  
−
<blockquote>
+
{| align="center" border="1" cellpadding="6" cellspacing="0" style="text-align:center; width:90%"
−
<p>Consider what effects that might conceivably have practical bearings you conceive the objects of your conception to have.  Then, your conception of those effects is the whole of your conception of the object.</p>
+
|+ style="height:30px" | <math>\text{Table A9.} ~~ \text{Tangent Proposition}~ \mathrm{d}f = \text{Pointwise Linear Approximation to the Difference Map}~ \mathrm{D}f\!</math>
 +
|- style="background:ghostwhite; height:40px"
 +
| style="border-right:none" | <math>f\!</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\mathrm{d}f =
 +
\\[2pt]
 +
\partial_x f \cdot \mathrm{d}x ~+~ \partial_y f \cdot \mathrm{d}y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\mathrm{d}^2\!f =
 +
\\[2pt]
 +
\partial_{xy} f \cdot \mathrm{d}x\;\mathrm{d}y
 +
\end{matrix}</math>
 +
| <math>\mathrm{d}f|_{x \, y}</math>
 +
| <math>\mathrm{d}f|_{x \, \texttt{(} y \texttt{)}}</math>
 +
| <math>\mathrm{d}f|_{\texttt{(} x \texttt{)} \, y}</math>
 +
| <math>\mathrm{d}f|_{\texttt{(} x \texttt{)(} y \texttt{)}}</math>
 +
|-
 +
| style="border-right:none" | <math>f_0\!</math>
 +
| style="border-left:4px double black" | <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
|-
 +
| style="border-right:none" |
 +
<math>\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}\!</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y
 +
\\
 +
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y
 +
\\
 +
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
\mathrm{d}x\;\mathrm{d}y
 +
\\
 +
\mathrm{d}x\;\mathrm{d}y
 +
\\
 +
\mathrm{d}x\;\mathrm{d}y
 +
\\
 +
\mathrm{d}x\;\mathrm{d}y
 +
\end{matrix}</math>
 +
| <math>\begin{matrix}0\\\mathrm{d}x\\\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x\\0\\\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\\0\\\mathrm{d}x\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\\\mathrm{d}x\\0\end{matrix}</math>
 +
|-
 +
| style="border-right:none" |
 +
<math>\begin{matrix}f_{3}\\f_{12}\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}</math>
 +
| <math>\begin{matrix}0\\0\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}</math>
 +
|-
 +
| style="border-right:none" |
 +
<math>\begin{matrix}f_{6}\\f_{9}\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}\mathrm{d}x & + & \mathrm{d}y\\\mathrm{d}x & + & \mathrm{d}y\end{matrix}</math>
 +
| <math>\begin{matrix}0\\0\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}</math>
 +
|-
 +
| style="border-right:none" |
 +
<math>\begin{matrix}f_{5}\\f_{10}\end{matrix}\!</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\!</math>
 +
| <math>\begin{matrix}0\\0\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\!</math>
 +
| <math>\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\!</math>
 +
| <math>\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\!</math>
 +
| <math>\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\!</math>
 +
|-
 +
| style="border-right:none" |
 +
<math>\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y
 +
\\
 +
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y
 +
\end{matrix}\!</math>
 +
| <math>\begin{matrix}
 +
\mathrm{d}x\;\mathrm{d}y
 +
\\
 +
\mathrm{d}x\;\mathrm{d}y
 +
\\
 +
\mathrm{d}x\;\mathrm{d}y
 +
\\
 +
\mathrm{d}x\;\mathrm{d}y
 +
\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\\\mathrm{d}x\\0\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\\0\\\mathrm{d}x\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x\\0\\\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\end{matrix}</math>
 +
| <math>\begin{matrix}0\\\mathrm{d}x\\\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}</math>
 +
|-
 +
| style="border-right:none" | <math>f_{15}\!</math>
 +
| style="border-left:4px double black" | <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
|}
  
−
<p>[[Charles Sanders Peirce]], "The Maxim of Pragmatism, CP 5.438.</p>
+
<br>
−
</blockquote>
 
  
−
One other subject that it would be opportune to mention at this point, while we have an object example of a mathematical group fresh in mind, is the relationship between the pragmatic maxim and what are commonly known in mathematics as ''representation principles''.  As it turns out, with regard to its formal characteristics, the pragmatic maxim unites the aspects of a representation principle with the attributes of what would ordinarily be known as a ''closure principle''.  We will consider the form of closure that is invoked by the pragmatic maxim on another occasion, focusing here and now on the topic of group representations.
+
====Table A10. Taylor Series Expansion Df = d''f'' + d<sup>2</sup>''f''====
  
−
Let us return to the example of the so-called ''four-group'' ''V''<sub>4</sub>.  We encountered this group in one of its concrete representations, namely, as a ''transformation group'' that acts on a set of objects, in this particular case a set of sixteen functions or propositions.  Forgetting about the set of objects that the group transforms among themselves, we may take the abstract view of the group's operational structure, say, in the form of the group operation table copied here:
+
<br>
  
−
<pre>
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:center; width:90%"
−
o---------o---------o---------o---------o---------o
+
|+ style="height:30px" |
−
|        %        |        |        |        |
+
<math>\text{Table A10.} ~~ \text{Taylor Series Expansion}~ {\mathrm{D}f = \mathrm{d}f + \mathrm{d}^2\!f}\!</math>
−
|    .    %    e    |    f    |    g    |    h    |
+
|- style="background:ghostwhite; height:40px"
−
|        %        |        |        |        |
+
| style="border-right:none" | <math>f\!</math>
−
o=========o=========o=========o=========o=========o
+
| style="border-left:4px double black" |
−
|         %        |        |        |        |
+
<math>\begin{matrix}
−
|    e    %    e    |    f   |    g    |    h    |
+
\mathrm{D}f
−
|         %        |        |        |        |
+
\\
−
o---------o---------o---------o---------o---------o
+
= & \mathrm{d}f & + & \mathrm{d}^2\!f
−
|         %        |        |        |        |
+
\\
−
|   f    %    f    |    e    |    h    |    g    |
+
= & \partial_x f \cdot \mathrm{d}x ~+~ \partial_y f \cdot \mathrm{d}y & + & \partial_{xy} f \cdot \mathrm{d}x\;\mathrm{d}y
−
|        %        |        |        |        |
+
\end{matrix}</math>
−
o---------o---------o---------o---------o---------o
+
| <math>\mathrm{d}f|_{x \, y}</math>
−
|        %        |        |        |        |
+
| <math>\mathrm{d}f|_{x \, \texttt{(} y \texttt{)}}</math>
−
|    g    %    g    |    h    |    e    |    f   |
+
| <math>\mathrm{d}f|_{\texttt{(} x \texttt{)} \, y}</math>
−
|        %        |        |        |        |
+
| <math>\mathrm{d}f|_{\texttt{(} x \texttt{)(} y \texttt{)}}</math>
−
o---------o---------o---------o---------o---------o
+
|-
−
|        %        |        |        |        |
+
| style="border-right:none" | <math>f_0\!</math>
−
|   h    %    h    |    g    |    f   |    e    |
+
| style="border-left:4px double black" | <math>0\!</math>
−
|         %        |         |        |        |
+
| <math>0\!</math>
−
o---------o---------o---------o---------o---------o
+
| <math>0\!</math>
−
</pre>
+
| <math>0\!</math>
−
 
+
| <math>0\!</math>
−
This table is abstractly the same as, or isomorphic to, the versions with the ''E''<sub>''ij''</sub> operators and the ''T''<sub>''ij''</sub> transformations that we discussed earlier.  That is to say, the story is the same — only the names have been changed.  An abstract group can have a multitude of significantly and superficially different representations.  Even after we have long forgotten the details of the particular representation that we may have come in with, there are species of concrete representations, called the ''regular representations'', that are always readily available, as they can be generated from the mere data of the abstract operation table itself.
+
|-
−
 
+
| style="border-right:none" | <math>\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}</math>
−
For example, select a group element from the top margin of the Table, and "consider its effects" on each of the group elements as they are listed along the left margin.  We may record these effects as Peirce usually did, as a logical "aggregate" of elementary dyadic relatives, that is to say, a disjunction or a logical sum whose terms represent the ordered pairs of <input : output> transactions that are produced by each group element in turn.  This yields what is usually known as one of the ''regular representations'' of the group, specifically, the ''first'', the ''post-'', or the ''right'' regular representation.  It has long been conventional to organize the terms in the form of a matrix:
+
| style="border-left:4px double black" |
−
 
+
<math>\begin{matrix}
−
Reading "+" as a logical disjunction:
+
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + &
−
 
+
\texttt{(} x \texttt{)} \cdot \mathrm{d}y & + &
−
<pre>
+
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
−
  G  =  e  +  f  +  g  + h,
+
\\
−
</pre>
+
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + &
−
 
+
\texttt{(} x \texttt{)} \cdot \mathrm{d}y & + &
−
And so, by expanding effects, we get:
+
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
−
 
+
\\
−
<pre>
+
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + &
−
  G  =  e:e  +  f:f  +  g:g  +  h:h
+
\texttt{~} x \texttt{~} \cdot \mathrm{d}y & + &
−
 
+
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
−
      +  e:f  +  f:e  +  g:h  +  h:g
+
\\
−
 
+
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + &
−
      +  e:g  +  f:h  +  g:e  +  h:f
+
\texttt{~} x \texttt{~} \cdot \mathrm{d}y & + &
−
 
+
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
−
      +  e:h  +  f:g  +  g:f  +  h:e
+
\end{matrix}</math>
−
</pre>
+
|
−
 
+
<math>\begin{matrix}
−
More on the pragmatic maxim as a representation principle later.
+
0\\\mathrm{d}x\\\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y
−
 
+
\end{matrix}</math>
−
===Note 10===
+
|
−
 
+
<math>\begin{matrix}
−
<blockquote>
+
\mathrm{d}x\\0\\\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y
−
<p>Consider what effects that might ''conceivably'' have practical bearings you ''conceive'' the objects of your ''conception'' to have.  Then, your ''conception'' of those effects is the whole of your ''conception'' of the object.</p>
+
\end{matrix}</math>
−
 
+
|
−
<p>Peirce, "Maxim of Pragmaticism", ''Collected Papers'', CP 5.438.</p>
+
<math>\begin{matrix}
−
</blockquote>
+
\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\\0\\\mathrm{d}x
−
 
+
\end{matrix}</math>
−
The genealogy of this conception of pragmatic representation is very intricate.  I will delineate some details that I presently fancy I remember clearly enough, subject to later correction.  Without checking historical accounts, I will not be able to pin down anything like a real chronology, but most of these notions were standard furnishings of the 19th Century mathematical study, and only the last few items date as late as the 1920's.
+
|
−
 
+
<math>\begin{matrix}
−
The idea about the regular representations of a group is universally known as ''Cayley's Theorem'', usually in the form: "Every group is isomorphic to a subgroup of ''Aut''(''X''), the group of automorphisms of an appropriate set ''X''".  There is a considerable generalization of these regular representations to a broad class of relational algebraic systems in Peirce's earliest papers.  The crux of the whole idea is this:
+
\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\\\mathrm{d}x\\0
−
 
+
\end{matrix}</math>
−
<pre>
+
|-
−
  Contemplate the effects of the symbol
+
| style="border-right:none" | <math>\begin{matrix}f_{3}\\f_{12}\end{matrix}</math>
−
  whose meaning you wish to investigate
+
| style="border-left:4px double black" |
−
  as they play out on all the stages of
+
<math>\begin{matrix}
−
  conduct on which you have the ability
+
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x & + &
−
  to imagine that symbol playing a role.
+
\texttt{~} 0 \texttt{~} \cdot \mathrm{d}y & + &
−
</pre>
+
\texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
−
 
+
\\
−
This idea of contextual definition is basically the same as Jeremy Bentham's notion of ''paraphrasis'', a "method of accounting for fictions by explaining various purported terms away" (Quine, in Van Heijenoort, p. 216).  Today we'd call these constructions ''term models''.  This, again, is the big idea behind Schönfinkel's combinators {S, K, I}, and hence of lambda calculus, and I reckon you know where that leads.
+
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x & + &
−
 
+
\texttt{~} 0 \texttt{~} \cdot \mathrm{d}y & + &
−
===Note 11===
+
\texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
−
 
+
\end{matrix}</math>
−
Let me return to Peirce's early papers on the algebra of relatives to pick up the conventions that he used there, and then rewrite my account of regular representations in a way that conforms to those.
+
|
−
 
+
<math>\begin{matrix}
−
Peirce expresses the action of an "elementary dual relative" like so:
+
\mathrm{d}x\\\mathrm{d}x
−
 
+
\end{matrix}</math>
−
<blockquote>
+
|
−
[Let] ''A'':''B'' be taken to denote the elementary relative which multiplied into ''B'' gives ''A''.  (Peirce, CP 3.123).
+
<math>\begin{matrix}
−
</blockquote>
+
\mathrm{d}x\\\mathrm{d}x
−
 
+
\end{matrix}</math>
−
And though he is well aware that it is not at all necessary to arrange elementary relatives into arrays, matrices, or tables, when he does so he tends to prefer organizing dyadic relations in the following manner:
+
|
−
 
+
<math>\begin{matrix}
−
<pre>
+
\mathrm{d}x\\\mathrm{d}x
−
  [  A:A  A:B  A:C  |
+
\end{matrix}</math>
−
  |                  |
+
|
−
  |  B:A  B:B  B:C  |
+
<math>\begin{matrix}
−
  |                  |
+
\mathrm{d}x\\\mathrm{d}x
−
  | C:A  C:B  C:C  ]
+
\end{matrix}</math>
−
</pre>
+
|-
−
 
+
| style="border-right:none" | <math>\begin{matrix}f_{6}\\f_{9}\end{matrix}</math>
−
That conforms to the way that the last school of thought I matriculated into stipulated that we tabulate material:
+
| style="border-left:4px double black" |
−
 
+
<math>\begin{matrix}
−
<pre>
+
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x & + &
−
  [  e_11  e_12  e_13  |
+
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}y & + &
−
  |                   |
+
\texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
−
  | e_21  e_22  e_23  |
+
\\
−
  |                    |
+
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x & + &
−
  | e_31  e_32  e_33  ]
+
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}y & + &
−
</pre>
+
\texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
−
 
+
\end{matrix}</math>
−
So, for example, let us suppose that we have the small universe {A, B, C}, and the 2-adic relation ''m'' = ''mover of'' that is represented by this matrix:
 
−
 
 
−
<pre>
 
−
  m  =
 
−
 
 
−
  [  m_AA (A:A)  m_AB (A:B)  m_AC (A:C)  |
 
−
  |                                        |
 
−
  |  m_BA (B:A)  m_BB (B:B)  m_BC (B:C)  |
 
−
  |                                        |
 
−
  |  m_CA (C:A)  m_CB (C:B)  m_CC (C:C)  ]
 
−
</pre>
 
−
 
 
−
Also, let ''m'' be such that:
 
−
 
 
−
<pre>
 
−
  A is a mover of A and B,
 
−
  B is a mover of B and C,
 
−
  C is a mover of C and A.
 
−
</pre>
 
−
 
 
−
In sum:
 
−
 
 
−
<pre>
 
−
  m  =
 
−
 
 
−
  [  1 * (A:A)  1 * (A:B)  0 * (A:C)  |
 
−
  |                                     |
 
−
  | 0 * (B:A)  1 * (B:B)  1 * (B:C)  |
 
−
  |                                    |
 
−
  |  1 * (C:A)  0 * (C:B)  1 * (C:C)  ]
 
−
</pre>
 
−
 
 
−
For the sake of orientation and motivation, compare with Peirce's notation in CP 3.329.
 
−
 
 
−
I think that will serve to fix notation and set up the remainder of the account.
 
−
 
 
−
===Note 12===
 
−
 
 
−
<pre>
 
−
It is common in algebra to switch around
 
−
between different conventions of display,
 
−
as the momentary fancy happens to strike,
 
−
and I see that Peirce is no different in
 
−
this sort of shiftiness than anyone else.
 
−
A changeover appears to occur especially
 
−
whenever he shifts from logical contexts
 
−
to algebraic contexts of application.
 
−
 
 
−
In the paper "On the Relative Forms of Quaternions" (CP 3.323),
 
−
we observe Peirce providing the following sorts of explanation:
 
−
 
 
−
| If X, Y, Z denote the three rectangular components of a vector, and W denote
 
−
| numerical unity (or a fourth rectangular component, involving space of four
 
−
| dimensions), and (Y:Z) denote the operation of converting the Y component
 
−
| of a vector into its Z component, then
 
 
|
 
|
−
|    1  =  (W:W) + (X:X) + (Y:Y) + (Z:Z)
+
<math>\begin{matrix}
 +
\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y
 +
\end{matrix}</math>
 
|
 
|
−
|    i  =  (X:W) - (W:X) - (Y:Z) + (Z:Y)
+
<math>\begin{matrix}
 +
\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y
 +
\end{matrix}</math>
 
|
 
|
−
|    j  =  (Y:W) - (W:Y) - (Z:X) + (X:Z)
+
<math>\begin{matrix}
 +
\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y
 +
\end{matrix}</math>
 
|
 
|
−
|     k  = (Z:W) - (W:Z) - (X:Y) + (Y:X)
+
<math>\begin{matrix}
 +
\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y
 +
\end{matrix}</math>
 +
|-
 +
| style="border-right:none" | <math>\begin{matrix}f_{5}\\f_{10}\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~} 0 \texttt{~} \cdot \mathrm{d}x & + &
 +
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}y & + &
 +
\texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
 +
\\
 +
\texttt{~} 0 \texttt{~} \cdot \mathrm{d}x & + &
 +
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}y & + &
 +
\texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
 +
\end{matrix}</math>
 
|
 
|
−
| In the language of logic (Y:Z) is a relative term whose relate is
+
<math>\begin{matrix}
−
| a Y component, and whose correlate is a Z component.  The law of
+
\mathrm{d}y\\\mathrm{d}y
−
| multiplication is plainly (Y:Z)(Z:X) = (Y:X), (Y:Z)(X:W) = 0,
+
\end{matrix}</math>
−
| and the application of these rules to the above values of
 
−
| 1, i, j, k gives the quaternion relations
 
 
|
 
|
−
|    i^2  =  j^2  =  k^2  =  -1,
+
<math>\begin{matrix}
 +
\mathrm{d}y\\\mathrm{d}y
 +
\end{matrix}</math>
 
|
 
|
−
|    ijk  =  -1,
+
<math>\begin{matrix}
 +
\mathrm{d}y\\\mathrm{d}y
 +
\end{matrix}</math>
 
|
 
|
−
|     etc.
+
<math>\begin{matrix}
 +
\mathrm{d}y\\\mathrm{d}y
 +
\end{matrix}</math>
 +
|-
 +
| style="border-right:none" | <math>\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}</math>
 +
| style="border-left:4px double black" |
 +
<math>\begin{matrix}
 +
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + &
 +
\texttt{~} x \texttt{~} \cdot \mathrm{d}y & + &
 +
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + &
 +
\texttt{~} x \texttt{~} \cdot \mathrm{d}y & + &
 +
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
 +
\\
 +
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + &
 +
\texttt{(} x \texttt{)} \cdot \mathrm{d}y & + &
 +
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + &
 +
\texttt{(} x \texttt{)} \cdot \mathrm{d}y & + &
 +
\texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y
 +
\end{matrix}</math>
 
|
 
|
−
| The symbol a(Y:Z) denotes the changing of Y to Z and the
+
<math>\begin{matrix}
−
| multiplication of the result by 'a'.  If the relatives be
+
\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\\\mathrm{d}x\\0
−
| arranged in a block
+
\end{matrix}</math>
 
|
 
|
−
|    W:W    W:X    W:Y    W:Z
+
<math>\begin{matrix}
 +
\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\\0\\\mathrm{d}x
 +
\end{matrix}</math>
 
|
 
|
−
|    X:W    X:X    X:Y    X:Z
+
<math>\begin{matrix}
 +
\mathrm{d}x\\0\\\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y
 +
\end{matrix}</math>
 
|
 
|
−
|     Y:W    Y:X    Y:Y    Y:Z
+
<math>\begin{matrix}
 +
0\\\mathrm{d}x\\\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y
 +
\end{matrix}</math>
 +
|-
 +
| style="border-right:none" | <math>f_{15}\!</math>
 +
| style="border-left:4px double black" | <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
|}
 +
 
 +
<br>
 +
 
 +
====Table A11. Partial Differentials and Relative Differentials====
 +
 
 +
<br>
 +
 
 +
{| align="center" border="1" cellpadding="6" cellspacing="0" style="text-align:center; width:90%"
 +
|+ style="height:30px" | <math>\text{Table A11.} ~~ \text{Partial Differentials and Relative Differentials}\!</math>
 +
|- style="background:ghostwhite; height:50px"
 +
| &nbsp;
 +
| <math>f\!</math>
 +
| <math>\frac{\partial f}{\partial x}\!</math>
 +
| <math>\frac{\partial f}{\partial y}\!</math>
 
|
 
|
−
|     Z:W    Z:X    Z:Y    Z:Z
+
<math>\begin{matrix}
 +
\mathrm{d}f =
 +
\\[2pt]
 +
\partial_x f \cdot \mathrm{d}x ~+~ \partial_y f \cdot \mathrm{d}y
 +
\end{matrix}</math>
 +
| <math>\left. \frac{\partial x}{\partial y} \right| f\!</math>
 +
| <math>\left. \frac{\partial y}{\partial x} \right| f\!</math>
 +
|-
 +
| <math>f_0\!</math>
 +
| <math>\texttt{(~)}\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
|-
 +
| <math>\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}</math>
 
|
 
|
−
| then the quaternion w + xi + yj + zk
+
<math>\begin{matrix}
−
| is represented by the matrix of numbers
+
\texttt{(} x \texttt{)(} y \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)~} y \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~(} y \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~~} y \texttt{~}
 +
\end{matrix}</math>
 
|
 
|
−
|    w      -x      -y     -z
+
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\\
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\end{matrix}</math>
 
|
 
|
−
|    x       w      -z      y
+
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~}
 +
\end{matrix}</math>
 
|
 
|
−
|     y        z      w      -x
+
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y
 +
\\
 +
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y
 +
\\
 +
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y
 +
\end{matrix}</math>
 +
| <math>\begin{matrix}\cdots\\\cdots\\\cdots\\\cdots\end{matrix}</math>
 +
| <math>\begin{matrix}\cdots\\\cdots\\\cdots\\\cdots\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{3}\\f_{12}\end{matrix}</math>
 
|
 
|
−
|     z      -y      x      w
+
<math>\begin{matrix}
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{~} x \texttt{~}
 +
\end{matrix}</math>
 +
| <math>\begin{matrix}1\\1\end{matrix}</math>
 +
| <math>\begin{matrix}0\\0\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}</math>
 +
| <math>\begin{matrix}\cdots\\\cdots\end{matrix}</math>
 +
| <math>\begin{matrix}\cdots\\\cdots\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{6}\\f_{9}\end{matrix}</math>
 
|
 
|
−
| The multiplication of such matrices follows the same laws as the
+
<math>\begin{matrix}
−
| multiplication of quaternions.  The determinant of the matrix =
+
\texttt{~(} x \texttt{,~} y \texttt{)~}
−
| the fourth power of the tensor of the quaternion.
+
\\
 +
\texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| <math>\begin{matrix}1\\1\end{matrix}</math>
 +
| <math>\begin{matrix}1\\1\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}x & + & \mathrm{d}y\\\mathrm{d}x & + & \mathrm{d}y\end{matrix}</math>
 +
| <math>\begin{matrix}\cdots\\\cdots\end{matrix}</math>
 +
| <math>\begin{matrix}\cdots\\\cdots\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{5}\\f_{10}\end{matrix}</math>
 
|
 
|
−
| The imaginary x + y(-1)^(1/2) may likewise be represented by the matrix
+
<math>\begin{matrix}
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\end{matrix}</math>
 +
| <math>\begin{matrix}0\\0\end{matrix}</math>
 +
| <math>\begin{matrix}1\\1\end{matrix}</math>
 +
| <math>\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}</math>
 +
| <math>\begin{matrix}\cdots\\\cdots\end{matrix}</math>
 +
| <math>\begin{matrix}\cdots\\\cdots\end{matrix}</math>
 +
|-
 +
| <math>\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}</math>
 
|
 
|
−
|      x     y
+
<math>\begin{matrix}
 +
\texttt{(~} x \texttt{~~} y \texttt{~)}
 +
\\
 +
\texttt{(~} x \texttt{~(} y \texttt{))}
 +
\\
 +
\texttt{((} x \texttt{)~} y \texttt{~)}
 +
\\
 +
\texttt{((} x \texttt{)(} y \texttt{))}
 +
\end{matrix}</math>
 
|
 
|
−
|    -y     x
+
<math>\begin{matrix}
 +
\texttt{~} y \texttt{~}
 +
\\
 +
\texttt{(} y \texttt{)}
 +
\\
 +
\texttt{~} y \texttt{~}
 +
\\
 +
\texttt{(} y \texttt{)}
 +
\end{matrix}</math>
 
|
 
|
−
| and the determinant of the matrix = the square of the modulus.
+
<math>\begin{matrix}
 +
\texttt{~} x \texttt{~}
 +
\\
 +
\texttt{~} x \texttt{~}
 +
\\
 +
\texttt{(} x \texttt{)}
 +
\\
 +
\texttt{(} x \texttt{)}
 +
\end{matrix}</math>
 
|
 
|
−
| C.S. Peirce, 'Collected Papers', CP 3.323, (1882).
+
<math>\begin{matrix}
−
|'Johns Hopkins University Circulars', No. 13, p. 179.
+
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y
 +
\\
 +
\texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y
 +
\\
 +
\texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y
 +
\end{matrix}</math>
 +
| <math>\begin{matrix}\cdots\\\cdots\\\cdots\\\cdots\end{matrix}</math>
 +
| <math>\begin{matrix}\cdots\\\cdots\\\cdots\\\cdots\end{matrix}</math>
 +
|-
 +
| <math>f_{15}\!</math>
 +
| <math>\texttt{((~))}\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
| <math>0\!</math>
 +
|}
 +
 
 +
<br>
 +
 
 +
====Table A12. Detail of Calculation for the Difference Map====
  
−
This way of talking is the mark of a person who opts
+
<br>
−
to multiply his matrices "on the right", as they say.
+
 
−
Yet Peirce still continues to call the first element
+
{| align="center" cellpadding="6" cellspacing="0" style="border-bottom:4px double black; border-left:4px double black; border-right:4px double black; border-top:4px double black; text-align:center; width:80%"
−
of the ordered pair (i:j) its "relate" while calling
+
|+ style="height:30px" | <math>\text{Table A12.} ~~ \text{Detail of Calculation for}~ {\mathrm{E}f + f = \mathrm{D}f}\!</math>
−
the second element of the pair (i:j) its "correlate".
+
|- style="background:ghostwhite"
−
That doesn't comport very well, so far as I can tell,
+
| style="width:6%" | &nbsp;
−
with his customary reading of relative terms, suited
+
| style="width:14%; border-left:1px solid black"  | <math>f\!</math>
−
more to the multiplication of matrices "on the left".
+
| style="width:20%; border-left:4px double black" |
 +
<math>\begin{array}{cr}
 +
~ & \mathrm{E}f|_{\mathrm{d}x ~ \mathrm{d}y}
 +
\\[4pt]
 +
+ & f|_{\mathrm{d}x ~ \mathrm{d}y}
 +
\\[4pt]
 +
= & \mathrm{D}f|_{\mathrm{d}x ~ \mathrm{d}y}
 +
\end{array}</math>
 +
| style="width:20%; border-left:1px solid black" |
 +
<math>\begin{array}{cr}
 +
~ & \mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y}
 +
\\[4pt]
 +
+ & f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y}
 +
\\[4pt]
 +
= & \mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y}
 +
\end{array}</math>
 +
| style="width:20%; border-left:1px solid black" |
 +
<math>\begin{array}{cr}
 +
~ & \mathrm{E}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}}
 +
\\[4pt]
 +
+ & f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}}
 +
\\[4pt]
 +
= & \mathrm{D}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}}
 +
\end{array}</math>
 +
| style="width:20%; border-left:1px solid black" |
 +
<math>\begin{array}{cr}
 +
~ & \mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}}
 +
\\[4pt]
 +
+ & f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}}
 +
\\[4pt]
 +
= & \mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}}
 +
\end{array}</math>
 +
|-
 +
| style="border-top:4px double black" | <math>f_{0}\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black"  | <math>0\!</math>
 +
| style="border-top:4px double black; border-left:4px double black" | <math>0 ~+~ 0 ~=~ 0\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black"  | <math>0 ~+~ 0 ~=~ 0\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black"  | <math>0 ~+~ 0 ~=~ 0\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black"  | <math>0 ~+~ 0 ~=~ 0\!</math>
 +
|-
 +
| style="border-top:4px double black" | <math>f_{1}\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\texttt{~(} x \texttt{)(} y \texttt{)~}\!</math>
 +
| style="border-top:4px double black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~~} x \texttt{~~} y \texttt{~~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{)(} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~~} x \texttt{~(} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{)(} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{~~} ~ \texttt{~(} y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{)~} y \texttt{~~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{)(} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{~(} x \texttt{)~} ~ \texttt{~~}
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{)(} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{)(} y \texttt{)~}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{2}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\texttt{~(} x \texttt{)~} y \texttt{~~}\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~~} x \texttt{~(} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{)~} y \texttt{~~}
 +
\\[4pt]
 +
= & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~~} x \texttt{~~} y \texttt{~~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{)~} y \texttt{~~}
 +
\\[4pt]
 +
= & \texttt{~~} ~ \texttt{~~} y \texttt{~~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{)(} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{)~} y \texttt{~~}
 +
\\[4pt]
 +
= & \texttt{~(} x \texttt{)~} ~ \texttt{~~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{)~} y \texttt{~~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{)~} y \texttt{~~}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{4}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\texttt{~~} x \texttt{~(} y \texttt{)~}\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{)~} y \texttt{~~}
 +
\\[4pt]
 +
+ & \texttt{~~} x \texttt{~(} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{)(} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~~} x \texttt{~(} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{~~} ~ \texttt{~(} y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~~} x \texttt{~~} y \texttt{~~}
 +
\\[4pt]
 +
+ & \texttt{~~} x \texttt{~(} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{~~} x \texttt{~~} ~ \texttt{~~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~~} x \texttt{~(} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~~} x \texttt{~(} y \texttt{)~}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{8}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\texttt{~~} x \texttt{~~} y \texttt{~~}\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{)(} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~~} x \texttt{~~} y \texttt{~~}
 +
\\[4pt]
 +
= & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{)~} y \texttt{~~}
 +
\\[4pt]
 +
+ & \texttt{~~} x \texttt{~~} y \texttt{~~}
 +
\\[4pt]
 +
= & \texttt{~~} ~ \texttt{~~} y \texttt{~~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~~} x \texttt{~(} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~~} x \texttt{~~} y \texttt{~~}
 +
\\[4pt]
 +
= & \texttt{~~} x \texttt{~~} ~ \texttt{~~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~~} x \texttt{~~} y \texttt{~~}
 +
\\[4pt]
 +
+ & \texttt{~~} x \texttt{~~} y \texttt{~~}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:4px double black" | <math>f_{3}\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\texttt{(} x \texttt{)}\!</math>
 +
| style="border-top:4px double black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & x
 +
\\[4pt]
 +
+ & \texttt{(} x \texttt{)}
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & x
 +
\\[4pt]
 +
+ & \texttt{(} x \texttt{)}
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{(} x \texttt{)}
 +
\\[4pt]
 +
+ & \texttt{(} x \texttt{)}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{(} x \texttt{)}
 +
\\[4pt]
 +
+ & \texttt{(} x \texttt{)}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{12}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>x\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{(} x \texttt{)}
 +
\\[4pt]
 +
+ & x
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{(} x \texttt{)}
 +
\\[4pt]
 +
+ & x
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & x
 +
\\[4pt]
 +
+ & x
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & x
 +
\\[4pt]
 +
+ & x
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:4px double black" | <math>f_{6}\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\texttt{~(} x \texttt{,~} y \texttt{)~}\!</math>
 +
| style="border-top:4px double black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{9}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\texttt{((} x \texttt{,~} y \texttt{))}\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:4px double black" | <math>f_{5}\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\texttt{(} y \texttt{)}\!</math>
 +
| style="border-top:4px double black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & y
 +
\\[4pt]
 +
+ & \texttt{(} y \texttt{)}
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{(} y \texttt{)}
 +
\\[4pt]
 +
+ & \texttt{(} y \texttt{)}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & y
 +
\\[4pt]
 +
+ & \texttt{(} y \texttt{)}
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{(} y \texttt{)}
 +
\\[4pt]
 +
+ & \texttt{(} y \texttt{)}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{10}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>y\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{(} y \texttt{)}
 +
\\[4pt]
 +
+ & y
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & y
 +
\\[4pt]
 +
+ & y
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{(} y \texttt{)}
 +
\\[4pt]
 +
+ & y
 +
\\[4pt]
 +
= & 1
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & y
 +
\\[4pt]
 +
+ & y
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:4px double black" | <math>f_{7}\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\texttt{~(} x \texttt{~~} y \texttt{)~}\!</math>
 +
| style="border-top:4px double black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{)(} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{~~} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{)~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{~~} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{~~} ~ \texttt{~~} y \texttt{~~}
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{~(} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{~~} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{~~} x \texttt{~~} ~ \texttt{~~}
 +
\end{matrix}</math>
 +
| style="border-top:4px double black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{~~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{~~} y \texttt{)~}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{11}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\texttt{~(} x \texttt{~(} y \texttt{))}\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{)~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{~(} y \texttt{))}
 +
\\[4pt]
 +
= & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{)(} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{~(} y \texttt{))}
 +
\\[4pt]
 +
= & \texttt{~~} ~ \texttt{~(} y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{~~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{~(} y \texttt{))}
 +
\\[4pt]
 +
= & \texttt{~~} x \texttt{~~} ~ \texttt{~~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{~(} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{~(} x \texttt{~(} y \texttt{))}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{13}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\texttt{((} x \texttt{)~} y \texttt{)~}\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{~(} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{)~} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{~(} x \texttt{,~} y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{~~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{)~} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{~~} ~ \texttt{~~} y \texttt{~~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{)(} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{)~} y \texttt{)~}
 +
\\[4pt]
 +
= & \texttt{~(} x \texttt{)~} ~ \texttt{~~}
 +
\end{matrix}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{)~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{)~} y \texttt{)~}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:1px solid black" | <math>f_{14}\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\texttt{((} x \texttt{)(} y \texttt{))}\!</math>
 +
| style="border-top:1px solid black; border-left:4px double black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{~~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{)(} y \texttt{))}
 +
\\[4pt]
 +
= & \texttt{((} x \texttt{,~} y \texttt{))}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{~(} x \texttt{~(} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{)(} y \texttt{))}
 +
\\[4pt]
 +
= & \texttt{~~} ~ \texttt{~(} y \texttt{)~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{)~} y \texttt{)~}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{)(} y \texttt{))}
 +
\\[4pt]
 +
= & \texttt{~(} x \texttt{)~} ~ \texttt{~~}
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
~ & \texttt{((} x \texttt{)(} y \texttt{))}
 +
\\[4pt]
 +
+ & \texttt{((} x \texttt{)(} y \texttt{))}
 +
\\[4pt]
 +
= & 0
 +
\end{matrix}</math>
 +
|-
 +
| style="border-top:4px double black" | <math>f_{15}\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black"  | <math>1\!</math>
 +
| style="border-top:4px double black; border-left:4px double black" | <math>1 ~+~ 1 ~=~ 0\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black"  | <math>1 ~+~ 1 ~=~ 0\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black"  | <math>1 ~+~ 1 ~=~ 0\!</math>
 +
| style="border-top:4px double black; border-left:1px solid black" | <math>1 ~+~ 1 ~=~ 0\!</math>
 +
|}
  
−
So I still have a few wrinkles to iron out before
+
<br>
−
I can give this story a smooth enough consistency.
 
−
</pre>
 
  
−
===Note 13===
+
===Appendix 3. Computational Details===
  
−
<pre>
+
====Operator Maps for the Logical Conjunction ''f''<sub>8</sub>(u, v)====
−
Let us make up the model universe $1$ = A + B + C and the 2-adic relation
 
−
n = "noter of", as when "X is a data record that contains a pointer to Y".
 
−
That interpretation is not important, it's just for the sake of intuition.
 
−
In general terms, the 2-adic relation n can be represented by this matrix:
 
  
−
  n  =
+
=====Computation of &epsilon;''f''<sub>8</sub>=====
  
−
  [  n_AA (A:A)  n_AB (A:B)  n_AC (A:C)  |
+
<br>
−
  |                                        |
 
−
  |  n_BA (B:A)  n_BB (B:B)  n_BC (B:C)  |
 
−
  |                                        |
 
−
  |  n_CA (C:A)  n_CB (C:B)  n_CC (C:C)  ]
 
  
−
Also, let n be such that:
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F8.1} ~~ \text{Computation of}~ \boldsymbol\varepsilon f_{8}~\!</math>
 +
|
 +
<math>\begin{array}{*{10}{l}}
 +
\boldsymbol\varepsilon f_{8}
 +
& = && f_{8}(u, v)
 +
\\[4pt]
 +
& = && uv
 +
\\[4pt]
 +
& = && uv \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + &  uv \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v
 +
& + &  uv \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)}
 +
& + &  uv \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\\[20pt]
 +
\boldsymbol\varepsilon f_{8}
 +
& = && uv \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&& + & uv \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
\\[4pt]
 +
&& + & uv \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&& + & uv \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
\end{array}\!</math>
 +
|}
  
−
  A is a noter of A and B,
+
<br>
−
  B is a noter of B and C,
 
−
  C is a noter of C and A.
 
  
−
Filling in the instantial values of the "coefficients" n_ij,
+
=====Computation of E''f''<sub>8</sub>=====
−
as the indices i and j range over the universe of discourse:
 
  
−
  n  =
+
<br>
  
−
  [  1 * (A:A)   1 * (A:B)   0 * (A:C)  |
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
−
  |                                    |
+
|+ style="height:30px" | <math>\text{Table F8.2-i} ~~ \text{Computation of}~ \mathrm{E}f_{8} ~\text{(Method 1)}\!</math>
−
  | 0 * (B:A)   1 * (B:B)   1 * (B:C)  |
+
|
−
  |                                    |
+
<math>\begin{array}{*{9}{l}}
−
  |  1 * (C:A)   0 * (C:B)   1 * (C:C) ]
+
\mathrm{E}f_{8}
 +
& = & f_{8}(u + \mathrm{d}u, v + \mathrm{d}v)
 +
\\[4pt]
 +
& = & \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)(} v \texttt{,} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
& = & \texttt{ } u \texttt{ } v \texttt{ } \cdot f_{8}(\texttt{(} \mathrm{d}u \texttt{)}, \texttt{(} \mathrm{d}v \texttt{)})
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot f_{8}(\texttt{(} \mathrm{d}u \texttt{)}, \mathrm{d}v)
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot f_{8}(\mathrm{d}u, \texttt{(} \mathrm{d}v \texttt{)})
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot f_{8}(\mathrm{d}u, \mathrm{d}v)
 +
\\[4pt]
 +
& = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\\[20pt]
 +
\mathrm{E}f_{8}
 +
& = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&&& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v
 +
\\[4pt]
 +
&&&&& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&&&&&&& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\end{array}\!</math>
 +
|}
  
−
In Peirce's time, and even in some circles of mathematics today,
+
<br>
−
the information indicated by the elementary relatives (i:j), as
 
−
i, j range over the universe of discourse, would be referred to
 
−
as the "umbral elements" of the algebraic operation represented
 
−
by the matrix, though I seem to recall that Peirce preferred to
 
−
call these terms the "ingredients".  When this ordered basis is
 
−
understood well enough, one will tend to drop any mention of it
 
−
from the matrix itself, leaving us nothing but these bare bones:
 
  
−
  n =
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F8.2-ii} ~~ \text{Computation of}~ \mathrm{E}f_{8} ~\text{(Method 2)}\!</math>
 +
|
 +
<math>\begin{array}{*{9}{c}}
 +
\mathrm{E}f_{8}
 +
& = & (u + \mathrm{d}u) \cdot (v + \mathrm{d}v)
 +
\\[6pt]
 +
& = & u \cdot v
 +
& + & u \cdot \mathrm{d}v
 +
& + & v \cdot \mathrm{d}u
 +
& + & \mathrm{d}u \cdot \mathrm{d}v
 +
\\[6pt]
 +
\mathrm{E}f_{8}
 +
& = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\end{array}\!</math>
 +
|}
  
−
  [  1  1  0  |
+
<br>
−
  |          |
 
−
  |  0  1  1  |
 
−
  |          |
 
−
  |  1  0  1  ]
 
  
−
However the specification may come to be written, this
+
=====Computation of D''f''<sub>8</sub>=====
−
is all just convenient schematics for stipulating that:
 
  
−
  n  =  A:A  +  B:B  +  C:C  +  A:B  +  B:C  +  C:A
+
<br>
  
−
Recognizing !1! = A:A + B:B + C:C to be the identity transformation,
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
−
the 2-adic relation n = "noter of" may be represented by an element
+
|+ style="height:30px" | <math>\text{Table F8.3-i} ~~ \text{Computation of}~ \mathrm{D}f_{8} ~\text{(Method 1)}\!</math>
−
!1! + A:B + B:C + C:A of the so-called "group ring", all of which
+
|
−
just makes this element a special sort of linear transformation.
+
<math>\begin{array}{*{10}{l}}
 +
\mathrm{D}f_{8}
 +
& = && \mathrm{E}f_{8}
 +
& + &  \boldsymbol\varepsilon f_{8}
 +
\\[4pt]
 +
& = && f_{8}(u + \mathrm{d}u, v + \mathrm{d}v)
 +
& + &  f_{8}(u, v)
 +
\\[4pt]
 +
& = && \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)(} v \texttt{,} \mathrm{d}v \texttt{)}
 +
& + &  uv
 +
\\[20pt]
 +
\mathrm{D}f_{8}
 +
& = && 0
 +
& + &  0
 +
& + &  0
 +
& + &  0
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{~(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~~}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  0
 +
& + &  0
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{~~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)~}
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + &  0
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{~~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~~}
 +
& + &  0
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~} \mathrm{d}v \texttt{~}
 +
\\[20pt]
 +
\mathrm{D}f_{8}
 +
& = && \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~} \mathrm{d}v \texttt{~}
 +
\end{array}\!</math>
 +
|}
  
−
Up to this point, we are still reading the elementary relatives of
+
<br>
−
the form i:j in the way that Peirce reads them in logical contexts:
 
−
i is the relate, j is the correlate, and in our current example we
 
−
read i:j, or more exactly, n_ij = 1, to say that i is a noter of j.
 
−
This is the mode of reading that we call "multiplying on the left".
 
  
−
In the algebraic, permutational, or transformational contexts of
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
−
application, however, Peirce converts to the alternative mode of
+
|+ style="height:30px" | <math>\text{Table F8.3-ii} ~~ \text{Computation of}~ \mathrm{D}f_{8} ~\text{(Method 2)}\!</math>
−
reading, although still calling i the relate and j the correlate,
+
|
−
the elementary relative i:j now means that i gets changed into j.
+
<math>\begin{array}{*{9}{l}}
−
In this scheme of reading, the transformation A:B + B:C + C:A is
+
\mathrm{D}f_{8}
−
a permutation of the aggregate $1$ = A + B + C, or what we would
+
& = & \boldsymbol\varepsilon f_{8}
−
now call the set {A, B, C}, in particular, it is the permutation
+
& + & \mathrm{E}f_{8}
−
that is otherwise notated as:
+
\\[6pt]
 +
& = & f_{8}(u, v)
 +
& + & f_{8}(u + \mathrm{d}u, v + \mathrm{d}v)
 +
\\[6pt]
 +
& = & uv
 +
& + & \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)(} v \texttt{,} \mathrm{d}v \texttt{)}
 +
\\[6pt]
 +
& = & 0
 +
& + & u \cdot \mathrm{d}v
 +
& + & v \cdot \mathrm{d}u
 +
& + & \mathrm{d}u ~ \mathrm{d}v
 +
\\[6pt]
 +
\mathrm{D}f_{8}
 +
& = & 0
 +
& + & u \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v
 +
& + & v \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{((} u \texttt{,} v \texttt{))} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\end{array}</math>
 +
|}
  
−
  ( A B C )
+
<br>
−
  <       >
 
−
  ( B C A )
 
  
−
This is consistent with the convention that Peirce uses in
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
−
the paper "On a Class of Multiple Algebras" (CP 3.324-327).
+
|+ style="height:30px" | <math>\text{Table F8.3-iii} ~~ \text{Computation of}~ \mathrm{D}f_{8} ~\text{(Method 3)}\!</math>
−
</pre>
+
|
 +
<math>\begin{array}{c*{9}{l}}
 +
\mathrm{D}f_{8}
 +
& = & \boldsymbol\varepsilon f_{8} ~+~ \mathrm{E}f_{8}
 +
\\[20pt]
 +
\boldsymbol\varepsilon f_{8}
 +
& = &  u \,\cdot\, v \,\cdot\, \texttt{(} \mathrm{d}u \texttt{)} \texttt{(} \mathrm{d}v \texttt{)}
 +
& + &  u \,\cdot\, v \,\cdot\, \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & ~ u \,\cdot\, v \,\cdot\, \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & ~ u \;\cdot\; v \;\cdot\; \mathrm{d}u ~ \mathrm{d}v
 +
\\[6pt]
 +
\mathrm{E}f_{8}
 +
& = & u \,\cdot\, v \,\cdot\, \texttt{(} \mathrm{d}u \texttt{)} \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & u ~ \texttt{(} v \texttt{)}  \cdot  \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} ~ v \,\cdot\, \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)} \texttt{(} v \texttt{)} \cdot\, \mathrm{d}u ~ \mathrm{d}v
 +
\\[20pt]
 +
\mathrm{D}f_{8}
 +
& = & ~ ~ 0 ~~ \cdot ~ \texttt{(} \mathrm{d}u \texttt{)} \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & ~ ~ u ~~ \cdot ~ \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & ~ ~ ~ v ~~ \cdot ~ \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{((} u \texttt{,} v \texttt{))} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\end{array}\!</math>
 +
|}
  
−
===Note 14===
+
=====Computation of d''f''<sub>8</sub>=====
  
−
<pre>
+
<br>
−
We have been contemplating the virtues and the utilities of
 
−
the pragmatic maxim as a standard heuristic in hermeneutics,
 
−
that is, as a principle of interpretation that guides us in
 
−
finding clarifying representations for a problematic corpus
 
−
of symbols by means of their actions on other symbols or in
 
−
terms of their effects on the syntactic contexts wherein we
 
−
discover them or where we might conceive to distribute them.
 
  
−
I began this excursion by taking off from the moving platform
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
−
of differential logic and passing by way of the corresponding
+
|+ style="height:30px" | <math>\text{Table F8.4} ~~ \text{Computation of}~ \mathrm{d}f_{8}\!</math>
−
transformation groups, as they act on propositions, and on to
+
|
−
an exercise in applying the pragmatic maxim, by contemplating
+
<math>\begin{array}{c*{8}{l}}
−
the regular representations of groups as giving us one of the
+
\mathrm{D}f_{8}
−
simplest conceivable, relatively concrete applications of the
+
& = & uv \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
−
general principle of representation in question.
+
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\\[6pt]
 +
\Downarrow
 +
\\[6pt]
 +
\mathrm{d}f_{8}
 +
& = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0
 +
\end{array}</math>
 +
|}
  
−
There are a few problems of implementation that have to be worked out
+
<br>
−
in practice, most of which are cleared up by keeping in mind which of
 
−
several possible conventions we have chosen to follow at a given time.
 
  
−
But there does appear to remain this rather more substantial question:
+
=====Computation of r''f''<sub>8</sub>=====
−
Are the effects we seek relates or correlates, or does it even matter?
 
  
−
I will have to leave that question as it is for now,
+
<br>
−
in hopes that a solution will evolve itself in time.
 
−
</pre>
 
  
−
===Note 15===
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F8.5} ~~ \text{Computation of}~ \mathrm{r}f_{8}\!</math>
 +
|
 +
<math>\begin{array}{c*{8}{l}}
 +
\mathrm{r}f_{8} & = & \mathrm{D}f_{8} ~+~ \mathrm{d}f_{8}
 +
\\[20pt]
 +
\mathrm{D}f_{8}
 +
& = & uv \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\\[6pt]
 +
\mathrm{d}f_{8}
 +
& = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0
 +
\\[20pt]
 +
\mathrm{r}f_{8}
 +
& = & uv \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\end{array}</math>
 +
|}
  
−
<pre>
+
<br>
−
Obstacles to Applying the Pragmatic Maxim
 
  
−
No sooner do you get a good idea and try to apply it
+
=====Computation Summary for Conjunction=====
−
than you find that a motley array of obstacles arise.
 
  
−
It would be good if we could in practice more consistently
+
<br>
−
apply the pragmatic maxim to the purpose for which it was
 
−
purportedly intended by its author.  That aim would be
 
−
the clarification of concepts, that is, intellectual
 
−
symbols or mental signs, to the point where their
 
−
inherent senses, or their lacks thereof, would
 
−
be rendered manifest to suitable interpreters.
 
  
−
There are big obstacles and little obstacles to applying the pragmatic maxim.
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
−
In good subgoaling fashion, I will merely mention a few of the bigger blocks,
+
|+ style="height:30px" | <math>\text{Table F8.6} ~~ \text{Computation Summary for}~ f_{8}(u, v) = uv\!</math>
−
as if in passing, but not really getting past them, and then I will get down
+
|
−
to the details of the problems that more immediately obstruct our advance.
+
<math>\begin{array}{c*{8}{l}}
 +
\boldsymbol\varepsilon f_{8}
 +
& = & uv \cdot 1
 +
& + & u \texttt{(} v \texttt{)} \cdot 0
 +
& + & \texttt{(} u \texttt{)} v \cdot 0
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0
 +
\\[6pt]
 +
\mathrm{E}f_{8}
 +
& = & uv \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\\[6pt]
 +
\mathrm{D}f_{8}
 +
& = & uv \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\\[6pt]
 +
\mathrm{d}f_{8}
 +
& = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0
 +
\\[6pt]
 +
\mathrm{r}f_{8}
 +
& = & uv \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\end{array}</math>
 +
|}
  
−
Obstacle 1.  People do not always read the instructions very carefully.
+
<br>
−
There is a tendency in readers of particular prior persuasions to blow
 
−
the problem all out of proportion, to think that the maxim is meant to
 
−
reveal the absolutely positive and the totally unique meaning of every
 
−
preconception to which they might deign or elect to apply it.  Reading
 
−
the maxim with an even minimal attention, you can see that it promises
 
−
no such finality of unindexed sense, but ties what you conceive to you.
 
−
I have lately come to wonder at the tenacity of this misinterpretation.
 
−
Perhaps people reckon that nothing less would be worth their attention.
 
−
I am not sure.  I can only say the achievement of more modest goals is
 
−
the sort of thing on which our daily life depends, and there can be no
 
−
final end to inquiry nor any ultimate community without a continuation
 
−
of life, and that means life on a day to day basis.  All of which only
 
−
brings me back to the point of persisting with local meantime examples,
 
−
because if we can't apply the maxim there, we can't apply it anywhere.
 
−
</pre>
 
  
−
===Note 16===
+
====Operator Maps for the Logical Equality ''f''<sub>9</sub>(u, v)====
  
−
<pre>
+
=====Computation of &epsilon;''f''<sub>9</sub>=====
−
Obstacles to Applying the Pragmatic Maxim (cont.)
 
  
−
Obstacle 2.  Applying the pragmatic maxim, even with a moderate aim, can be hard.
+
<br>
−
I think that my present example, deliberately impoverished as it is, affords us
 
−
with an embarassing richness of evidence of just how complex the simple can be.
 
  
−
All the better reason for me to see if I can finish it up before moving on.
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F9.1} ~~ \text{Computation of}~ \boldsymbol\varepsilon f_{9}\!</math>
 +
|
 +
<math>\begin{array}{*{10}{l}}
 +
\boldsymbol\varepsilon f_{9}
 +
& = && f_{9}(u, v)
 +
\\[4pt]
 +
& = && \texttt{((} u \texttt{,~} v \texttt{))}
 +
\\[4pt]
 +
& = && \texttt{ } u \texttt{  } v \texttt{ } \cdot f_{9}(1, 1)
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot f_{9}(1, 0)
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \cdot f_{9}(0, 1)
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \cdot f_{9}(0, 0)
 +
\\[4pt]
 +
& = && u v & + & 0 & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)}
 +
\\[20pt]
 +
\boldsymbol\varepsilon f_{9}
 +
& = && \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + &  0
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  0
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + &  0
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
& + &  0
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
\end{array}</math>
 +
|}
  
−
Expressed most simply, the idea is to replace the question of "what it is",
+
<br>
−
which modest people know is far too difficult for them to answer right off,
 
−
with the question of "what it does", which most of us know a modicum about.
 
  
−
In the case of regular representations of groups we found
+
=====Computation of E''f''<sub>9</sub>=====
−
a non-plussing surplus of answers to sort our way through.
 
−
So let us track back one more time to see if we can learn
 
−
any lessons that might carry over to more realistic cases.
 
  
−
Here is is the operation table of V_4 once again:
+
<br>
  
−
Table 1.  Klein Four-Group V_4
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
−
o---------o---------o---------o---------o---------o
+
|+ style="height:30px" | <math>\text{Table F9.2} ~~ \text{Computation of}~ \mathrm{E}f_{9}\!</math>
−
|         %        |         |        |        |
+
|
−
|    .    %    e    |    f    |    g    |    h    |
+
<math>\begin{array}{*{10}{l}}
−
|        %        |        |        |        |
+
\mathrm{E}f_{9}
−
o=========o=========o=========o=========o=========o
+
& = && f_{9}(u + \mathrm{d}u, v + \mathrm{d}v)
−
|        %        |        |        |        |
+
\\[4pt]
−
|    e    %    e    |    f    |    g    |    h    |
+
& = && \texttt{(((} u \texttt{,} \mathrm{d}u \texttt{),(} v \texttt{,} \mathrm{d}v \texttt{)))}
−
|        %        |        |        |        |
+
\\[4pt]
−
o---------o---------o---------o---------o---------o
+
& = && \texttt{ } u \texttt{  } v \texttt{ } \!\cdot\! f_{9}(\texttt{(} \mathrm{d}u \texttt{)}, \texttt{(} \mathrm{d}v \texttt{)})
−
|        %        |        |        |        |
+
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! f_{9}(\texttt{(} \mathrm{d}u \texttt{)}, \texttt{ } \mathrm{d}v \texttt{ })
−
|    f    %    f    |    e    |    h    |    g    |
+
& + &  \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! f_{9}(\texttt{ } \mathrm{d}u \texttt{ }, \texttt{(} \mathrm{d}v \texttt{)})
−
|        %        |        |        |        |
+
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! f_{9}(\texttt{ } \mathrm{d}u \texttt{ }, \texttt{ } \mathrm{d}v \texttt{ })
−
o---------o---------o---------o---------o---------o
+
\\[4pt]
−
|        %        |        |        |        |
+
& = && \texttt{ } u \texttt{  } v \texttt{ } \!\cdot\! \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))}
−
|    g    %    g    |    h    |    e    |    f    |
+
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! \texttt{ (} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{) }
−
|        %        |        |        |        |
+
& + &  \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{ (} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{) }
−
o---------o---------o---------o---------o---------o
+
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))}
−
|        %        |        |        |        |
+
\\[20pt]
−
|    h    %    h    |    g    |    f    |    e    |
+
\mathrm{E}f_{9}
−
|         %        |        |        |        |
+
& = && \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
−
o---------o---------o---------o---------o---------o
+
& + &  0
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&& + & 0
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  0
 +
\\[4pt]
 +
&& + & 0
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + &  0
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
& + &  0
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
\end{array}</math>
 +
|}
  
−
A group operation table is really just a device for
+
<br>
−
recording a certain 3-adic relation, to be specific,
 
−
the set of triples of the form <x, y, z> satisfying
 
−
the equation x.y = z, where "." signifies the group
 
−
operation, usually omitted as understood in context.
 
  
−
In the case of V_4 = (G, .), where G is the "underlying set"
+
=====Computation of D''f''<sub>9</sub>=====
−
{e, f, g, h}, we have the 3-adic relation L(V_4) c G x G x G
 
−
whose triples are listed below:
 
  
−
  <e, e, e>
+
<br>
−
  <e, f, f>
 
−
  <e, g, g>
 
−
  <e, h, h>
 
  
−
  <f, e, f>
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
−
  <f, f, e>
+
|+ style="height:30px" | <math>\text{Table F9.3-i} ~~ \text{Computation of}~ \mathrm{D}f_{9} ~\text{(Method 1)}\!</math>
−
  <f, g, h>
+
|
−
  <f, h, g>
+
<math>\begin{array}{*{10}{l}}
 +
\mathrm{D}f_{9}
 +
& = && \mathrm{E}f_{9}
 +
& + &  \boldsymbol\varepsilon f_{9}
 +
\\[4pt]
 +
& = && f_{9}(u + \mathrm{d}u, v + \mathrm{d}v)
 +
& + &  f_{9}(u, v)
 +
\\[4pt]
 +
& = && \texttt{(((} u \texttt{,} \mathrm{d}u \texttt{),(} v \texttt{,} \mathrm{d}v \texttt{)))}
 +
& + &  \texttt{((} u \texttt{,} v \texttt{))}
 +
\\[20pt]
 +
\mathrm{D}f_{9}
 +
& = && 0
 +
& + &  0
 +
& + &  0
 +
& + &  0
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&& + & 0
 +
& + &  0
 +
& + &  0
 +
& + &  0
 +
\\[20pt]
 +
\mathrm{D}f_{9}
 +
& = && \texttt{ } u \texttt{  } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
\end{array}\!</math>
 +
|}
  
−
  <g, e, g>
+
<br>
−
  <g, f, h>
 
−
  <g, g, e>
 
−
  <g, h, f>
 
  
−
  <h, e, h>
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
−
  <h, f, g>
+
|+ style="height:30px" | <math>\text{Table F9.3-ii} ~~ \text{Computation of}~ \mathrm{D}f_{9} ~\text{(Method 2)}\!</math>
−
  <h, g, f>
+
|
−
  <h, h, e>
+
<math>\begin{array}{*{9}{l}}
 +
\mathrm{D}f_{9}
 +
& = & 0 \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & 1 \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & 1 \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v
 +
& + & 0 \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
\end{array}</math>
 +
|}
  
−
It is part of the definition of a group that the 3-adic
+
<br>
−
relation L c G^3 is actually a function L : G x G -> G.
 
−
It is from this functional perspective that we can see
 
−
an easy way to derive the two regular representations.
 
−
Since we have a function of the type L : G x G -> G,
 
−
we can define a couple of substitution operators:
 
  
−
1.  Sub(x, <_, y>) puts any specified x into
+
=====Computation of d''f''<sub>9</sub>=====
−
    the empty slot of the rheme <_, y>, with
 
−
    the effect of producing the saturated
 
−
    rheme <x, y> that evaluates to xy.
 
  
−
2.  Sub(x, <y, _>) puts any specified x into
+
<br>
−
    the empty slot of the rheme <y, _>, with
 
−
    the effect of producing the saturated
 
−
    rheme <y, x> that evaluates to yx.
 
  
−
In (1), we consider the effects of each x in its
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
−
practical bearing on contexts of the form <_, y>,
+
|+ style="height:30px" | <math>\text{Table F9.4} ~~ \text{Computation of}~ \mathrm{d}f_{9}\!</math>
−
as y ranges over G, and the effects are such that
+
|
−
x takes <_, y> into xy, for y in G, all of which
+
<math>\begin{array}{c*{8}{l}}
−
is summarily notated as x = {(y : xy) : y in G}.
+
\mathrm{D}f_{9}
−
The pairs (y : xy) can be found by picking an x
+
& = & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
−
from the left margin of the group operation table
+
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
−
and considering its effects on each y in turn as
+
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
−
these run across the top margin. This aspect of
+
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
−
pragmatic definition we recognize as the regular
+
\\[6pt]
−
ante-representation:
+
\Downarrow
 +
\\[6pt]
 +
\mathrm{d}f_{9}
 +
& = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
\end{array}</math>
 +
|}
  
−
  e  =  e:e  +  f:f  +  g:g  +  h:h
+
<br>
  
−
  f = e:f  +  f:e  +  g:h  +  h:g
+
=====Computation of r''f''<sub>9</sub>=====
  
−
  g  =  e:g  +  f:h  +  g:e  +  h:f
+
<br>
  
−
  h  = e:h  + f:g +  g:f + h:e
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F9.5} ~~ \text{Computation of}~ \mathrm{r}f_{9}\!</math>
 +
|
 +
<math>\begin{array}{c*{8}{l}}
 +
\mathrm{r}f_{9} & = & \mathrm{D}f_{9} ~+~ \mathrm{d}f_{9}
 +
\\[20pt]
 +
\mathrm{D}f_{9}
 +
& = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
\\[6pt]
 +
\mathrm{d}f_{9}
 +
& = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
\\[20pt]
 +
\mathrm{r}f_{9}
 +
& = & \texttt{ } u \texttt{ } v \texttt{ } \cdot 0
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot 0
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot 0
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0
 +
\end{array}</math>
 +
|}
  
−
In (2), we consider the effects of each x in its
+
<br>
−
practical bearing on contexts of the form <y, _>,
 
−
as y ranges over G, and the effects are such that
 
−
x takes <y, _> into yx, for y in G, all of which
 
−
is summarily notated as x = {(y : yx) : y in G}.
 
−
The pairs (y : yx) can be found by picking an x
 
−
from the top margin of the group operation table
 
−
and considering its effects on each y in turn as
 
−
these run down the left margin.  This aspect of
 
−
pragmatic definition we recognize as the regular
 
−
post-representation:
 
  
−
  e  = e:e  +  f:f  +  g:g  +  h:h
+
=====Computation Summary for Equality=====
  
−
  f  =  e:f  +  f:e  +  g:h  +  h:g
+
<br>
  
−
  g  = e:g  + f:h  + g:e  + h:f
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F9.6} ~~ \text{Computation Summary for}~ f_{9}(u, v) = \texttt{((} u \texttt{,} v \texttt{))}\!</math>
 +
|
 +
<math>\begin{array}{c*{8}{l}}
 +
\boldsymbol\varepsilon f_{9}
 +
& = & uv \cdot 1
 +
& + & u \texttt{(} v \texttt{)} \cdot 0
 +
& + & \texttt{(} u \texttt{)} v \cdot 0
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 1
 +
\\[6pt]
 +
\mathrm{E}f_{9}
 +
& = & uv \cdot \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))}
 +
\\[6pt]
 +
\mathrm{D}f_{9}
 +
& = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
\\[6pt]
 +
\mathrm{d}f_{9}
 +
& = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
\\[6pt]
 +
\mathrm{r}f_{9}
 +
& = & uv \cdot 0
 +
& + & u \texttt{(} v \texttt{)} \cdot 0
 +
& + & \texttt{(} u \texttt{)} v \cdot 0
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0
 +
\end{array}</math>
 +
|}
  
−
  h  =  e:h  +  f:g  +  g:f  +  h:e
+
<br>
  
−
If the ante-rep looks the same as the post-rep,
+
====Operator Maps for the Logical Implication ''f''<sub>11</sub>(u, v)====
−
now that I'm writing them in the same dialect,
 
−
that is because V_4 is abelian (commutative),
 
−
and so the two representations have the very
 
−
same effects on each point of their bearing.
 
−
</pre>
 
  
−
===Note 17===
+
=====Computation of &epsilon;''f''<sub>11</sub>=====
  
−
<pre>
+
<br>
−
So long as we're in the neighborhood, we might as well take in
 
−
some more of the sights, for instance, the smallest example of
 
−
a non-abelian (non-commutative) group.  This is a group of six
 
−
elements, say, G = {e, f, g, h, i, j}, with no relation to any
 
−
other employment of these six symbols being implied, of course,
 
−
and it can be most easily represented as the permutation group
 
−
on a set of three letters, say, X = {A, B, C}, usually notated
 
−
as G = Sym(X) or more abstractly and briefly, as Sym(3) or S_3.
 
−
Here are the permutation (= substitution) operations in Sym(X):
 
  
−
Table 1.  Permutations or Substitutions in Sym_{A, B, C}
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
−
o---------o---------o---------o---------o---------o---------o
+
|+ style="height:30px" | <math>\text{Table F11.1} ~~ \text{Computation of}~ \boldsymbol\varepsilon f_{11}\!</math>
−
|        |        |        |        |        |        |
+
|
−
|    e    |    f    |    g    |    h    |    i    |    j    |
+
<math>\begin{array}{*{10}{l}}
−
|        |        |        |        |        |        |
+
\boldsymbol\varepsilon f_{11}
−
o=========o=========o=========o=========o=========o=========o
+
& = && f_{11}(u, v)
−
|        |        |        |        |        |        |
+
\\[4pt]
−
| A B C | A B C | A B C | A B C |  A B C  |  A B C  |
+
& = && \texttt{(} u \texttt{(} v \texttt{))}
−
|        |        |        |        |        |        |
+
\\[4pt]
−
| | | | | | | | |  | | |  |  | | |  |  | | |  |  | | |  |
+
& = && \texttt{ } u \texttt{ } v \texttt{ } \cdot f_{11}(1, 1)
−
| v v v | v v v  | v v v  | v v v | v v v  | v v v  |
+
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot f_{11}(1, 0)
−
|        |        |        |        |        |        |
+
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot f_{11}(0, 1)
−
| A B C | C A B |  B C A  |  A C B  |  C B A  |  B A C  |
+
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot f_{11}(0, 0)
−
|         |        |        |        |        |        |
+
\\[4pt]
−
o---------o---------o---------o---------o---------o---------o
+
& = && \texttt{ } u \texttt{ } v \texttt{ }
 +
& + & 0
 +
& + & \texttt{(} u \texttt{) } v \texttt{ }
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)}
 +
\\[20pt]
 +
\boldsymbol\varepsilon f_{11}
 +
& = && \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + & 0
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + & 0
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + & 0
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
& + & 0
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
\end{array}\!</math>
 +
|}
  
−
Here is the operation table for S_3, given in abstract fashion:
+
<br>
  
−
Table 2.  Symmetric Group S_3
+
=====Computation of E''f''<sub>11</sub>=====
  
−
|                        ^
+
<br>
−
|                    e / \ e
 
−
|                      /  \
 
−
|                    /  e  \
 
−
|                  f / \  / \ f
 
−
|                  /  \ /  \
 
−
|                  /  f  \  f  \
 
−
|              g / \  / \  / \ g
 
−
|                /  \ /  \ /  \
 
−
|              /  g  \  g  \  g  \
 
−
|            h / \  / \  / \  / \ h
 
−
|            /  \ /  \ /  \ /  \
 
−
|            /  h  \  e  \  e  \  h  \
 
−
|        i / \  / \  / \  / \  / \ i
 
−
|          /  \ /  \ /  \ /  \ /  \
 
−
|        /  i  \  i  \  f  \  j  \  i  \
 
−
|      j / \  / \  / \  / \  / \  / \ j
 
−
|      /  \ /  \ /  \ /  \ /  \ /  \
 
−
|      (  j  \  j  \  j  \  i  \  h  \  j  )
 
−
|      \  / \  / \  / \  / \  / \  /
 
−
|        \ /  \ /  \ /  \ /  \ /  \ /
 
−
|        \  h  \  h  \  e  \  j  \  i  /
 
−
|          \  / \  / \  / \  / \  /
 
−
|          \ /  \ /  \ /  \ /  \ /
 
−
|            \  i  \  g  \  f  \  h  /
 
−
|            \  / \  / \  / \  /
 
−
|              \ /  \ /  \ /  \ /
 
−
|              \  f  \  e  \  g  /
 
−
|                \  / \  / \  /
 
−
|                \ /  \ /  \ /
 
−
|                  \  g  \  f  /
 
−
|                  \  / \  /
 
−
|                    \ /  \ /
 
−
|                    \  e  /
 
−
|                      \  /
 
−
|                      \ /
 
−
|                        v
 
  
−
By the way, we will meet with the symmetric group S_3 again
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
−
when we return to take up the study of Peirce's early paper
+
|+ style="height:30px" | <math>\text{Table F11.2} ~~ \text{Computation of}~ \mathrm{E}f_{11}\!</math>
−
"On a Class of Multiple Algebras" (CP 3.324-327), and also
+
|
−
his late unpublished work "The Simplest Mathematics" (1902)
+
<math>\begin{array}{*{10}{l}}
−
(CP 4.227-323), with particular reference to the section
+
\mathrm{E}f_{11}
−
that treats of "Trichotomic Mathematics" (CP 4.307-323).
+
& = && f_{11}(u + \mathrm{d}u, v + \mathrm{d}v)
−
</pre>
+
\\[4pt]
 +
& = &&
 +
\texttt{(}
 +
\\
 +
&&& \qquad \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)}
 +
\\
 +
&&& \texttt{(}
 +
\\
 +
&&& \qquad \texttt{(} v \texttt{,} \mathrm{d}v \texttt{)}
 +
\\
 +
&&& \texttt{))}
 +
\\[4pt]
 +
& = &&
 +
u v
 +
\!\cdot\!
 +
\texttt{((} \mathrm{d}u \texttt{)((} \mathrm{d}v \texttt{)))}
 +
& + &
 +
u \texttt{(} v \texttt{)}
 +
\!\cdot\!
 +
\texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + &
 +
\texttt{(} u \texttt{)} v
 +
\!\cdot\!
 +
\texttt{(} \mathrm{d}u \texttt{((} \mathrm{d}v \texttt{)))}
 +
& + &
 +
\texttt{(} u \texttt{)(} v \texttt{)}
 +
\!\cdot\!
 +
\texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))}
 +
\\[4pt]
 +
& = &&
 +
u v
 +
\!\cdot\!
 +
\texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)}
 +
& + &
 +
u \texttt{(} v \texttt{)}
 +
\!\cdot\!
 +
\texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + &
 +
\texttt{(} u \texttt{)} v
 +
\!\cdot\!
 +
\texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)}
 +
& + &
 +
\texttt{(} u \texttt{)(} v \texttt{)}
 +
\!\cdot\!
 +
\texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))}
 +
\\[20pt]
 +
\mathrm{E}f_{11}
 +
& = && \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&& + & 0
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + &  0
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
\end{array}</math>
 +
|}
  
−
===Note 18===
+
<br>
  
−
<pre>
+
=====Computation of D''f''<sub>11</sub>=====
−
By way of collecting a short-term pay-off for all the work that we
 
−
did on the regular representations of the Klein 4-group V_4, let us
 
−
write out as quickly as possible in "relative form" a minimal budget
 
−
of representations for the symmetric group on three letters, Sym(3).
 
−
After doing the usual bit of compare and contrast among the various
 
−
representations, we will have enough concrete material beneath our
 
−
abstract belts to tackle a few of the presently obscur'd details
 
−
of Peirce's early "Algebra + Logic" papers.
 
  
−
Table 1.  Permutations or Substitutions in Sym {A, B, C}
+
<br>
−
o---------o---------o---------o---------o---------o---------o
 
−
|        |        |        |        |        |        |
 
−
|    e    |    f    |    g    |    h    |    i    |    j    |
 
−
|        |        |        |        |        |        |
 
−
o=========o=========o=========o=========o=========o=========o
 
−
|        |        |        |        |        |        |
 
−
|  A B C  |  A B C  |  A B C  |  A B C  |  A B C  |  A B C  |
 
−
|        |        |        |        |        |        |
 
−
|  | | |  |  | | |  |  | | |  |  | | |  |  | | |  |  | | |  |
 
−
|  v v v  |  v v v  |  v v v  |  v v v  |  v v v  |  v v v  |
 
−
|        |        |        |        |        |        |
 
−
|  A B C  |  C A B  |  B C A  |  A C B  |  C B A  |  B A C  |
 
−
|        |        |        |        |        |        |
 
−
o---------o---------o---------o---------o---------o---------o
 
  
−
Writing this table in relative form generates
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
−
the following "natural representation" of S_3.
+
|+ style="height:30px" | <math>\text{Table F11.3-i} ~~ \text{Computation of}~ \mathrm{D}f_{11} ~\text{(Method 1)}\!</math>
 +
|
 +
<math>\begin{array}{*{10}{l}}
 +
\mathrm{D}f_{11}
 +
& = && \mathrm{E}f_{11}
 +
& + &  \boldsymbol\varepsilon f_{11}
 +
\\[4pt]
 +
& = && f_{11}(u + \mathrm{d}u, v + \mathrm{d}v)
 +
& + &  f_{11}(u, v)
 +
\\[4pt]
 +
& = &&
 +
\texttt{(} \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)}
 +
\texttt{(} \texttt{(} v \texttt{,} \mathrm{d}v \texttt{)}
 +
\texttt{))}
 +
& + &
 +
\texttt{(} u \texttt{(} v \texttt{))}
 +
\\[20pt]
 +
\mathrm{D}f_{11}
 +
& = && 0
 +
& + &  0
 +
& + &  0
 +
& + &  0
 +
\\[4pt]
 +
&& + & u v \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + &  u \texttt{(} v \texttt{)} \!\cdot\! \texttt{~(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~~}
 +
& + &  0
 +
& + &  0
 +
\\[4pt]
 +
&& + & 0
 +
& + &  u \texttt{(} v \texttt{)} \!\cdot\! \texttt{~~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)~}
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&& + & 0
 +
& + &  u \texttt{(} v \texttt{)} \!\cdot\! \texttt{~~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~~}
 +
& + &  \texttt{(} u \texttt{)} v \!\cdot\! \mathrm{d}u ~ \mathrm{d}v
 +
& + &  0
 +
\\[20pt]
 +
\mathrm{D}f_{11}
 +
& = && u v \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + &  u \texttt{(} v \texttt{)} \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + &  \texttt{(} u \texttt{)} v \!\cdot\! \mathrm{d}u ~ \mathrm{d}v
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
\end{array}</math>
 +
|}
  
−
  e  =  A:A + B:B + C:C
+
<br>
  
−
  f  = A:C + B:A + C:B
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F11.3-ii} ~~ \text{Computation of}~ \mathrm{D}f_{11} ~\text{(Method 2)}\!</math>
 +
|
 +
<math>\begin{array}{c*{9}{l}}
 +
\mathrm{D}f_{11}
 +
& = & \boldsymbol\varepsilon f_{11} ~+~ \mathrm{E}f_{11}
 +
\\[20pt]
 +
\boldsymbol\varepsilon f_{11}
 +
& = & u v \cdot 1
 +
& + & u \texttt{(} v \texttt{)} \cdot 0
 +
& + & \texttt{(} u \texttt{)} v \cdot 1
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 1
 +
\\[6pt]
 +
\mathrm{E}f_{11}
 +
& = &
 +
u v
 +
\cdot
 +
\texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)}
 +
& + &
 +
u \texttt{(} v \texttt{)}
 +
\cdot
 +
\texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + &
 +
\texttt{(} u \texttt{)} v
 +
\cdot
 +
\texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)}
 +
& + &
 +
\texttt{(} u \texttt{)(} v \texttt{)}
 +
\cdot
 +
\texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))}
 +
\\[20pt]
 +
\mathrm{D}f_{11}
 +
& = &
 +
u v
 +
\cdot
 +
\texttt{~(} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{~}
 +
& + &
 +
u \texttt{(} v \texttt{)}
 +
\cdot
 +
\texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + &
 +
\texttt{(} u \texttt{)} v
 +
\cdot
 +
\texttt{~} \mathrm{d}u ~ \mathrm{d}v \texttt{~}
 +
& + &
 +
\texttt{(} u \texttt{)(} v \texttt{)}
 +
\cdot
 +
\texttt{~} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)~}
 +
\end{array}</math>
 +
|}
  
−
  g  =  A:B + B:C + C:A
+
<br>
  
−
  h  = A:A + B:C + C:B
+
=====Computation of d''f''<sub>11</sub>=====
  
−
  i  =  A:C + B:B + C:A
+
<br>
  
−
  j  = A:B + B:A + C:C
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F11.4} ~~ \text{Computation of}~ \mathrm{d}f_{11}\!</math>
 +
|
 +
<math>\begin{array}{c*{8}{l}}
 +
\mathrm{D}f_{11}
 +
& = & u v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
\\[6pt]
 +
\Downarrow
 +
\\[6pt]
 +
\mathrm{d}f_{11}
 +
& = & u v \cdot \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & 0
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u
 +
\end{array}</math>
 +
|}
  
−
I have without stopping to think about it written out this natural
+
<br>
−
representation of S_3 in the style that comes most naturally to me,
 
−
to wit, the "right" way, whereby an ordered pair configured as X:Y
 
−
constitutes the turning of X into Y.  It is possible that the next
 
−
time we check in with CSP that we will have to adjust our sense of
 
−
direction, but that will be an easy enough bridge to cross when we
 
−
come to it.
 
−
</pre>
 
  
−
===Note 19===
+
=====Computation of r''f''<sub>11</sub>=====
  
−
<pre>
+
<br>
−
To construct the regular representations of S_3,
 
−
we pick up from the data of its operation table:
 
  
−
Table 1. Symmetric Group S_3
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F11.5} ~~ \text{Computation of}~ \mathrm{r}f_{11}\!</math>
 +
|
 +
<math>\begin{array}{c*{8}{l}}
 +
\mathrm{r}f_{11} & = & \mathrm{D}f_{11} ~+~ \mathrm{d}f_{11}
 +
\\[20pt]
 +
\mathrm{D}f_{11}
 +
& = & u v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
\\[6pt]
 +
\mathrm{d}f_{11}
 +
& = & u v \cdot \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & 0
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u
 +
\\[20pt]
 +
\mathrm{r}f_{11}
 +
& = & u v \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\end{array}</math>
 +
|}
  
−
|                        ^
+
<br>
−
|                    e / \ e
 
−
|                      /  \
 
−
|                    /  e  \
 
−
|                  f / \  / \ f
 
−
|                  /  \ /  \
 
−
|                  /  f  \  f  \
 
−
|              g / \  / \  / \ g
 
−
|                /  \ /  \ /  \
 
−
|              /  g  \  g  \  g  \
 
−
|            h / \  / \  / \  / \ h
 
−
|            /  \ /  \ /  \ /  \
 
−
|            /  h  \  e  \  e  \  h  \
 
−
|        i / \  / \  / \  / \  / \ i
 
−
|          /  \ /  \ /  \ /  \ /  \
 
−
|        /  i  \  i  \  f  \  j  \  i  \
 
−
|      j / \  / \  / \  / \  / \  / \ j
 
−
|      /  \ /  \ /  \ /  \ /  \ /  \
 
−
|      (  j  \  j  \  j  \  i  \  h  \  j  )
 
−
|      \  / \  / \  / \  / \  / \  /
 
−
|        \ /  \ /  \ /  \ /  \ /  \ /
 
−
|        \  h  \  h  \  e  \  j  \  i  /
 
−
|          \  / \  / \  / \  / \  /
 
−
|          \ /  \ /  \ /  \ /  \ /
 
−
|            \  i  \  g  \  f  \  h  /
 
−
|            \  / \  / \  / \  /
 
−
|              \ /  \ /  \ /  \ /
 
−
|              \  f  \  e  \  g  /
 
−
|                \  / \  / \  /
 
−
|                \ /  \ /  \ /
 
−
|                  \  g  \  f  /
 
−
|                  \  / \  /
 
−
|                    \ /  \ /
 
−
|                    \  e  /
 
−
|                      \  /
 
−
|                      \ /
 
−
|                        v
 
  
−
Just by way of staying clear about what we are doing,
+
=====Computation Summary for Implication=====
−
let's return to the recipe that we worked out before:
 
  
−
It is part of the definition of a group that the 3-adic
+
<br>
−
relation L c G^3 is actually a function L : G x G -> G.
 
−
It is from this functional perspective that we can see
 
−
an easy way to derive the two regular representations.
 
  
−
Since we have a function of the type L : G x G -> G,
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
−
we can define a couple of substitution operators:
+
|+ style="height:30px" | <math>\text{Table F11.6} ~~ \text{Computation Summary for}~ f_{11}(u, v) = \texttt{(} u \texttt{(} v \texttt{))}\!</math>
 +
|
 +
<math>\begin{array}{c*{8}{l}}
 +
\boldsymbol\varepsilon f_{11}
 +
& = & u v \cdot 1
 +
& + & u \texttt{(} v \texttt{)} \cdot 0
 +
& + & \texttt{(} u \texttt{)} v \cdot 1
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 1
 +
\\[6pt]
 +
\mathrm{E}f_{11}
 +
& = & u v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))}
 +
\\[6pt]
 +
\mathrm{D}f_{11}
 +
& = & u v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
\\[6pt]
 +
\mathrm{d}f_{11}
 +
& = & u v \cdot \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & 0
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u
 +
\\[6pt]
 +
\mathrm{r}f_{11}
 +
& = & uv \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\end{array}</math>
 +
|}
  
−
1.  Sub(x, <_, y>) puts any specified x into
+
<br>
−
    the empty slot of the rheme <_, y>, with
 
−
    the effect of producing the saturated
 
−
    rheme <x, y> that evaluates to xy.
 
  
−
2.  Sub(x, <y, _>) puts any specified x into
+
====Operator Maps for the Logical Disjunction ''f''<sub>14</sub>(u, v)====
−
    the empty slot of the rheme <y, _>, with
 
−
    the effect of producing the saturated
 
−
    rheme <y, x> that evaluates to yx.
 
  
−
In (1), we consider the effects of each x in its
+
=====Computation of &epsilon;''f''<sub>14</sub>=====
−
practical bearing on contexts of the form <_, y>,
 
−
as y ranges over G, and the effects are such that
 
−
x takes <_, y> into xy, for y in G, all of which
 
−
is summarily notated as x = {(y : xy) : y in G}.
 
−
The pairs (y : xy) can be found by picking an x
 
−
from the left margin of the group operation table
 
−
and considering its effects on each y in turn as
 
−
these run along the right margin.  This produces
 
−
the regular ante-representation of S_3, like so:
 
  
−
  e  =  e:e  +  f:f  +  g:g  +  h:h  +  i:i  +  j:j
+
<br>
  
−
  f  =   e:f +  f:g +  g:e +  h:j +  i:h +  j:i
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F14.1} ~~ \text{Computation of}~ \boldsymbol\varepsilon f_{14}\!</math>
 +
|
 +
<math>\begin{array}{*{10}{l}}
 +
\boldsymbol\varepsilon f_{14}
 +
& = && f_{14}(u, v)
 +
\\[4pt]
 +
& = && \texttt{((} u \texttt{)(} v \texttt{))}
 +
\\[4pt]
 +
& = && \texttt{ } u \texttt{  } v \texttt{ } \cdot f_{14}(1, 1)
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot f_{14}(1, 0)
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \cdot f_{14}(0, 1)
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \cdot f_{14}(0, 0)
 +
\\[4pt]
 +
& = && \texttt{ } u \texttt{  } v \texttt{ }
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ }
 +
& + &  0
 +
\\[20pt]
 +
\boldsymbol\varepsilon f_{14}
 +
& = && \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + &  0
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + & 0
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + & 0
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
& + & 0
 +
\end{array}</math>
 +
|}
  
−
  g  =  e:g  +  f:e  +  g:f  +  h:i  +  i:j  +  j:h
+
<br>
  
−
  h  =   e:h  +  f:i  +  g:j  +  h:e  +  i:f  +  j:g
+
=====Computation of E''f''<sub>14</sub>=====
  
−
  i  =  e:i  +  f:j  +  g:h  +  h:g  +  i:e  +  j:f
+
<br>
  
−
  j  =   e:j +  f:h +  g:i +  h:f +  i:g +  j:e
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F14.2} ~~ \text{Computation of}~ \mathrm{E}f_{14}\!</math>
 +
|
 +
<math>\begin{array}{*{10}{l}}
 +
\mathrm{E}f_{14}
 +
& = && f_{14}(u + \mathrm{d}u, v + \mathrm{d}v)
 +
\\[4pt]
 +
& = &&
 +
\texttt{((}
 +
\\
 +
&&& \qquad \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)}
 +
\\
 +
&&& \texttt{)(}
 +
\\
 +
&&& \qquad \texttt{(} v \texttt{,} \mathrm{d}v \texttt{)}
 +
\\
 +
&&& \texttt{))}
 +
\\[4pt]
 +
& = && \texttt{ } u \texttt{ } v \texttt{ } \!\cdot\! f_{14}(\texttt{(} \mathrm{d}u \texttt{)}, \texttt{(} \mathrm{d}v \texttt{)})
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! f_{14}(\texttt{(} \mathrm{d}u \texttt{)}, \texttt{ } \mathrm{d}v \texttt{ })
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! f_{14}(\texttt{ } \mathrm{d}u \texttt{ }, \texttt{(} \mathrm{d}v \texttt{)})
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! f_{14}(\texttt{ } \mathrm{d}u \texttt{ }, \texttt{ } \mathrm{d}v \texttt{ })
 +
\\[4pt]
 +
& = && \texttt{ } u \texttt{  } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{~} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
\\[20pt]
 +
\mathrm{E}f_{14}
 +
& = && \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + &  \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
& + &  0
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{  } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
& + &  0
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~}
 +
\\[4pt]
 +
&& + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + & 0
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)}
 +
\\[4pt]
 +
&& + & 0
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~}
 +
\end{array}</math>
 +
|}
  
−
In (2), we consider the effects of each x in its
+
<br>
−
practical bearing on contexts of the form <y, _>,
 
−
as y ranges over G, and the effects are such that
 
−
x takes <y, _> into yx, for y in G, all of which
 
−
is summarily notated as x = {(y : yx) : y in G}.
 
−
The pairs (y : yx) can be found by picking an x
 
−
on the right margin of the group operation table
 
−
and considering its effects on each y in turn as
 
−
these run along the left margin.  This generates
 
−
the regular post-representation of S_3, like so:
 
  
−
  e  =   e:e  +  f:f  +  g:g  +  h:h  +  i:i  +  j:j
+
=====Computation of D''f''<sub>14</sub>=====
  
−
  f  =  e:f  +  f:g  +  g:e  +  h:i  +  i:j  +  j:h
+
<br>
  
−
  g  =   e:g +  f:e +  g:f +  h:j +  i:h +  j:i
+
{| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F14.3-i} ~~ \text{Computation of}~ \mathrm{D}f_{14} ~\text{(Method 1)}\!</math>
 +
|
 +
<math>\begin{array}{*{10}{l}}
 +
\mathrm{D}f_{14}
 +
& = && \mathrm{E}f_{14}
 +
& + &  \boldsymbol\varepsilon f_{14}
 +
\\[4pt]
 +
& = && f_{14}(u + \mathrm{d}u, v + \mathrm{d}v)
 +
& + &  f_{14}(u, v)
 +
\\[4pt]
 +
& = && \texttt{(((} u \texttt{,} \mathrm{d}u \texttt{))((} v \texttt{,} \mathrm{d}v \texttt{)))}
 +
& + &  \texttt{((} u \texttt{)(} v \texttt{))}
 +
\\[20pt]
 +
\mathrm{D}f_{14}
 +
& = && 0
 +
& + & 0
 +
& + & 0
 +
& + &  0
 +
\\[4pt]
 +
&& + & 0
 +
& + &  0
 +
& + &  \texttt{(} u \texttt{)} v \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{~(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~~}
 +
\\[4pt]
 +
&& + & 0
 +
& + &  u \texttt{(} v \texttt{)} \!\cdot\! \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & 0
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{~~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)~}
 +
\\[4pt]
 +
&& + & uv \!\cdot\! \mathrm{d}u ~ \mathrm{d}v
 +
& + & 0
 +
& + & 0
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{~~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~~}
 +
\\[20pt]
 +
\mathrm{D}f_{14}
 +
& = && uv \!\cdot\! \mathrm{d}u ~ \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \!\cdot\! \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)} v \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
\end{array}</math>
 +
|}
  
−
  h  =  e:h  +  f:j  +  g:i  +  h:e  +  i:g  +  j:f
+
<br>
  
−
  i  =   e:i  +  f:h  + g:j  + h:f  + i:e  + j:g
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F14.3-ii} ~~ \text{Computation of}~ \mathrm{D}f_{14} ~\text{(Method 2)}\!</math>
 +
|
 +
<math>\begin{array}{*{9}{l}}
 +
\mathrm{D}f_{14}
 +
& = & \texttt{((} u \texttt{,} v \texttt{))} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & 0 \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}
 +
\end{array}</math>
 +
|}
  
−
  j  =  e:j  +  f:i  +  g:h  +  h:g  +  i:f  +  j:e
+
<br>
  
−
If the ante-rep looks different from the post-rep,
+
=====Computation of d''f''<sub>14</sub>=====
−
it is just as it should be, as S_3 is non-abelian
 
−
(non-commutative), and so the two representations
 
−
differ in the details of their practical effects,
 
−
though, of course, being representations of the
 
−
same abstract group, they must be isomorphic.
 
−
</pre>
 
  
−
===Note 20===
+
<br>
  
−
<pre>
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
−
| the way of heaven and earth
+
|+ style="height:30px" | <math>\text{Table F14.4} ~~ \text{Computation of}~ \mathrm{d}f_{14}\!</math>
−
| is to be long continued
 
−
| in their operation
 
−
| without stopping
 
 
|
 
|
−
| i ching, hexagram 32
+
<math>\begin{array}{c*{8}{l}}
 +
\mathrm{D}f_{14}
 +
& = & \texttt{ } u \texttt{  } v \texttt{ } \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
\\[6pt]
 +
\Downarrow
 +
\\[6pt]
 +
\mathrm{d}f_{14}
 +
& = & \texttt{ } u \texttt{  } v \texttt{ } \cdot 0
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \mathrm{d}u
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
\end{array}</math>
 +
|}
  
−
You may be wondering what happened to the announced subject of "Differential Logic".
+
<br>
−
If you think that we have been taking a slight excursion my reply to the charge of
 
−
a scenic rout would be both "yes and no".  What happened was this.  We chanced to
 
−
make the observation that the shift operators E_ij form a transformation group
 
−
that acts on the set of propositions of the form f : B^2 -> B.  Group theory
 
−
is a very attractive subject, but it did not have the effect of drawing us
 
−
so far off our initial course as one might at first think.  For one thing,
 
−
groups, in particular, the special family of groups that have come to be
 
−
named after the Norwegian mathematician Marius Sophus Lie, turn out to
 
−
be of critical importance in the solution of differential equations.
 
−
For another thing, group operations afford us examples of 3-adic
 
−
relations that have been extremely well-studied over the years,
 
−
and thus they supply us with no small bit of guidance in the
 
−
study of sign relations, another class of 3-adic relations
 
−
that have significance for logical studies, in our brief
 
−
acquaintance with which we have scarcely even begun to
 
−
break the ice.  Finally, I could not resist taking up
 
−
the connection between group representations, which
 
−
constitute a very generic class of logical models,
 
−
and the all-important pragmatic maxim.
 
  
−
Biographical Data for Marius Sophus Lie (1842-1899):
+
=====Computation of r''f''<sub>14</sub>=====
−
http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Lie.html
 
−
</pre>
 
  
−
===Note 21===
+
<br>
  
−
<pre>
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
−
We've seen a couple of groups, V_4 and S_3, represented in various ways, and
+
|+ style="height:30px" | <math>\text{Table F14.5} ~~ \text{Computation of}~ \mathrm{r}f_{14}\!</math>
−
we've seen their representations presented in a variety of different manners.
+
|
−
Let us look at one other stylistic variant for presenting a representation
+
<math>\begin{array}{c*{8}{l}}
−
that is frequently seen, the so-called "matrix representation" of a group.
+
\mathrm{r}f_{14} & = & \mathrm{D}f_{14} ~+~ \mathrm{d}f_{14}
 +
\\[20pt]
 +
\mathrm{D}f_{14}
 +
& = & \texttt{ } u \texttt{  } v \texttt{ } \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
\\[6pt]
 +
\mathrm{d}f_{14}
 +
& = & \texttt{ } u \texttt{  } v \texttt{ } \cdot 0
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \mathrm{d}u
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
\\[20pt]
 +
\mathrm{r}f_{14}
 +
& = & \texttt{ } u \texttt{  } v \texttt{ } \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\end{array}</math>
 +
|}
  
−
Recalling the manner of our acquaintance with the symmetric group S_3,
+
<br>
−
we began with the "bigraph" (bipartite graph) picture of its natural
 
−
representation as the set of all permutations or substitutions on
 
−
the set X = {A, B, C}.
 
  
−
Table 1.  Permutations or Substitutions in Sym {A, B, C}
+
=====Computation Summary for Disjunction=====
−
o---------o---------o---------o---------o---------o---------o
 
−
|        |        |        |        |        |        |
 
−
|    e    |    f    |    g    |    h    |    i    |    j    |
 
−
|        |        |        |        |        |        |
 
−
o=========o=========o=========o=========o=========o=========o
 
−
|        |        |        |        |        |        |
 
−
|  A B C  |  A B C  |  A B C  |  A B C  |  A B C  |  A B C  |
 
−
|        |        |        |        |        |        |
 
−
|  | | |  |  | | |  |  | | |  |  | | |  |  | | |  |  | | |  |
 
−
|  v v v  |  v v v  |  v v v  |  v v v  |  v v v  |  v v v  |
 
−
|        |        |        |        |        |        |
 
−
|  A B C  |  C A B  |  B C A  |  A C B  |  C B A  |  B A C  |
 
−
|        |        |        |        |        |        |
 
−
o---------o---------o---------o---------o---------o---------o
 
  
−
Then we rewrote these permutations -- since they are
+
<br>
−
functions f : X -> X they can also be recognized as
 
−
2-adic relations f c X x X -- in "relative form",
 
−
in effect, in the manner to which Peirce would
 
−
have made us accustomed had he been given
 
−
a relative half-a-chance:
 
  
−
  e  = A:A + B:B + C:C
+
{| align="center" border="1" cellpadding="20" cellspacing="0" style="text-align:left; width:90%"
 +
|+ style="height:30px" | <math>\text{Table F14.6} ~~ \text{Computation Summary for}~ f_{14}(u, v) = \texttt{((} u \texttt{)(} v \texttt{))}\!</math>
 +
|
 +
<math>\begin{array}{c*{8}{l}}
 +
\boldsymbol\varepsilon f_{14}
 +
& = & uv \cdot 1
 +
& + & u \texttt{(} v \texttt{)} \cdot 1
 +
& + & \texttt{(} u \texttt{)} v \cdot 1
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0
 +
\\[6pt]
 +
\mathrm{E}f_{14}
 +
& = & uv \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))}
 +
& + & \texttt{(} u \texttt{)} v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
\\[6pt]
 +
\mathrm{D}f_{14}
 +
& = & uv \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
\\[6pt]
 +
\mathrm{d}f_{14}
 +
& = & uv \cdot 0
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
\\[6pt]
 +
\mathrm{r}f_{14}
 +
& = & uv \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
 +
\end{array}</math>
 +
|}
  
−
  f  =  A:C + B:A + C:B
+
<br>
  
−
  g  = A:B + B:C + C:A
+
===Appendix 4. Source Materials===
  
−
  h  = A:A + B:C + C:B
+
===Appendix 5. Various Definitions of the Tangent Vector===
  
−
  i  = A:C + B:B + C:A
+
==References==
  
−
  j =  A:B + B:A + C:C
+
* Ashby, William Ross (1956/1964), ''An Introduction to Cybernetics'', Chapman and Hall, London, UK, 1956. Reprinted, Methuen and Company, London, UK, 1964.
  
−
These days one is much more likely to encounter the natural representation
+
* Awbrey, J., and Awbrey, S. (1989), "Theme One : A Program of Inquiry", Unpublished Manuscript, 09 Aug 1989.  [http://web.archive.org/web/20071021145200/http://ndirty.cute.fi/~karttu/Awbrey/Theme1Prog/Theme1Guide.doc Microsoft Word Document].
−
of S_3 in the form of a "linear representation", that is, as a family of
 
−
linear transformations that map the elements of a suitable vector space
 
−
into each other, all of which would in turn usually be represented by
 
−
a set of matrices like these:
 
  
−
Table 2. Matrix Representations of the Permutations in Sym(3)
+
* Edelman, Gerald M. (1988), ''Topobiology : An Introduction to Molecular Embryology'', Basic Books, New York, NY.
−
o---------o---------o---------o---------o---------o---------o
 
−
|        |        |        |        |        |        |
 
−
|    e    |    f    |    g    |    h    |    i    |    j    |
 
−
|        |        |        |        |        |        |
 
−
o=========o=========o=========o=========o=========o=========o
 
−
|        |        |        |        |        |        |
 
−
|  1 0 0  |  0 0 1  |  0 1 0  |  1 0 0  |  0 0 1  |  0 1 0  |
 
−
|  0 1 0  |  1 0 0  |  0 0 1  |  0 0 1  |  0 1 0  |  1 0 0  |
 
−
|  0 0 1  |  0 1 0  |  1 0 0  |  0 1 0  |  1 0 0  |  0 0 1  |
 
−
|        |        |        |        |        |        |
 
−
o---------o---------o---------o---------o---------o---------o
 
  
−
The key to the mysteries of these matrices is revealed by noting that their
+
* Leibniz, Gottfried Wilhelm, Freiherr von, ''Theodicy : Essays on the Goodness of God, The Freedom of Man, and The Origin of Evil'', Austin Farrer (ed.), E.M. Huggard (trans.), based on C.J. Gerhardt (ed.), ''Collected Philosophical Works'', 1875&ndash;1890, Routledge and Kegan Paul, London, UK, 1951.  Reprinted, Open Court, La Salle, IL, 1985.
−
coefficient entries are arrayed and overlayed on a place mat marked like so:
 
  
−
  [ A:A  A:B  A:C |
+
* McClelland, James L., and Rumelhart, David E. (1988), ''Explorations in Parallel Distributed Processing : A Handbook of Models, Programs, and Exercises'', MIT Press, Cambridge, MA.
−
  | B:A  B:B  B:C |
 
−
  | C:A  C:B  C:C ]
 
  
−
Of course, the place-settings of convenience at different symposia may vary.
+
[[Category:Adaptive Systems]]
−
</pre>
+
[[Category:Artificial Intelligence]]
 +
[[Category:Boolean Algebra]]
 +
[[Category:Boolean Functions]]
 +
[[Category:Charles Sanders Peirce]]
 +
[[Category:Combinatorics]]
 +
[[Category:Computational Complexity]]
 +
[[Category:Computer Science]]
 +
[[Category:Cybernetics]]
 +
[[Category:Differential Logic]]
 +
[[Category:Discrete Systems]]
 +
[[Category:Dynamical Systems]]
 +
[[Category:Equational Reasoning]]
 +
[[Category:Formal Languages]]
 +
[[Category:Formal Sciences]]
 +
[[Category:Formal Systems]]
 +
[[Category:Graph Theory]]
 +
[[Category:Group Theory]]
 +
[[Category:Inquiry]]
 +
[[Category:Inquiry Driven Systems]]
 +
[[Category:Knowledge Representation]]
 +
[[Category:Linguistics]]
 +
[[Category:Logic]]
 +
[[Category:Logical Graphs]]
 +
[[Category:Mathematics]]
 +
[[Category:Mathematical Systems Theory]]
 +
[[Category:Philosophy]]
 +
[[Category:Propositional Calculus]]
 +
[[Category:Science]]
 +
[[Category:Semiotics]]
 +
[[Category:Systems Science]]
 +
[[Category:Visualization]]

Latest revision as of 03:24, 27 December 2016

Author: Jon Awbrey

A differential propositional calculus is a propositional calculus extended by a set of terms for describing aspects of change and difference, for example, processes that take place in a universe of discourse or transformations that map a source universe into a target universe.

Casual Introduction

Consider the situation represented by the venn diagram in Figure 1.

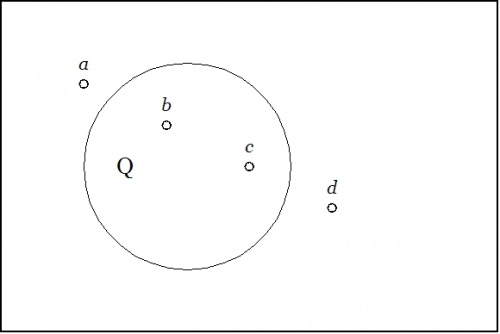
DiffPropCalc1.jpg
\(\text{Figure 1.} ~~ \text{Local Habitations, And Names}\!\)

The area of the rectangle represents a universe of discourse, \(X.\!\) This might be a population of individuals having various additional properties or it might be a collection of locations that various individuals occupy. The area of the “circle” represents the individuals that have the property \(q\!\) or the locations that fall within the corresponding region \(Q.\!\) Four individuals, \(a, b, c, d,\!\) are singled out by name. It happens that \(b\!\) and \(c\!\) currently reside in region \(Q\!\) while \(a\!\) and \(d\!\) do not.

Now consider the situation represented by the venn diagram in Figure 2.

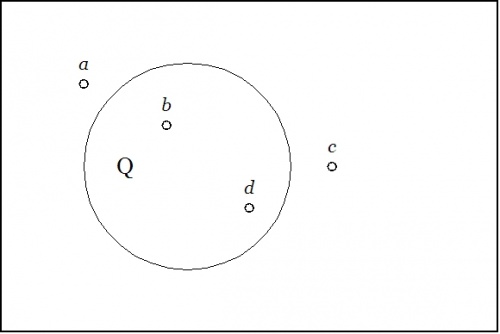
DiffPropCalc2.jpg
\(\text{Figure 2.} ~~ \text{Same Names, Different Habitations}\!\)

Figure 2 differs from Figure 1 solely in the circumstance that the object \(c\!\) is outside the region \(Q\!\) while the object \(d\!\) is inside the region \(Q.\!\) So far, there is nothing that says that our encountering these Figures in this order is other than purely accidental, but if we interpret the present sequence of frames as a “moving picture” representation of their natural order in a temporal process, then it would be natural to say that \(a\!\) and \(b\!\) have remained as they were with regard to quality \(q\!\) while \(c\!\) and \(d\!\) have changed their standings in that respect. In particular, \(c\!\) has moved from the region where \(q\!\) is \(\mathrm{true}\!\) to the region where \(q\!\) is \(\mathrm{false}\!\) while \(d\!\) has moved from the region where \(q\!\) is \(\mathrm{false}\!\) to the region where \(q\!\) is \(\mathrm{true}.\!\)

Figure 3 reprises the situation shown in Figure 1, but this time interpolates a new quality that is specifically tailored to account for the relation between Figure 1 and Figure 2.

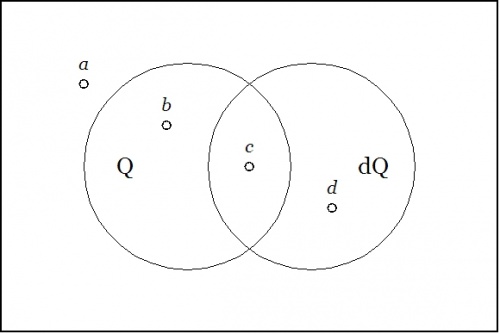
DiffPropCalc3.jpg
\(\text{Figure 3.} ~~ \text{Back, To The Future}\!\)

This new quality, \(\mathrm{d}q,\!\) is an example of a differential quality, since its absence or presence qualifies the absence or presence of change occurring in another quality. As with any other quality, it is represented in the venn diagram by means of a “circle” that distinguishes two halves of the universe of discourse, in this case, the portions of \(X\!\) outside and inside the region \(\mathrm{d}Q.\!\)

Figure 1 represents a universe of discourse, \(X,\!\) together with a basis of discussion, \(\{ q \},\!\) for expressing propositions about the contents of that universe. Once the quality \(q\!\) is given a name, say, the symbol \({}^{\backprime\backprime} q {}^{\prime\prime},\!\) we have the basis for a formal language that is specifically cut out for discussing \(X\!\) in terms of \(q,\!\) and this formal language is more formally known as the propositional calculus with alphabet \(\{ {}^{\backprime\backprime} q {}^{\prime\prime} \}.\!\)

In the context marked by \(X\!\) and \(\{ q \}\!\) there are but four different pieces of information that can be expressed in the corresponding propositional calculus, namely, the propositions\[\mathrm{false}, ~ \lnot q, ~ q, ~ \mathrm{true}.\!\] Referring to the sample of points in Figure 1, the constant proposition \(\mathrm{false}\!\) holds of no points, the proposition \(\lnot q\!\) holds of \(a\!\) and \(d,\!\) the proposition \(q\!\) holds of \(b\!\) and \(c,\!\) and the constant proposition \(\mathrm{true}\!\) holds of all points in the sample.

Figure 3 preserves the same universe of discourse and extends the basis of discussion to a set of two qualities, \(\{ q, \mathrm{d}q \}.\!\) In parallel fashion, the initial propositional calculus is extended by means of the enlarged alphabet, \(\{ {}^{\backprime\backprime} q {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{d}q {}^{\prime\prime} \}.\!\) Any propositional calculus over two basic propositions allows for the expression of 16 propositions all together. Just by way of salient examples in the present setting, we can pick out the most informative propositions that apply to each of our sample points. Using overlines to express logical negation, these are given as follows:

  • \(\overline{q} ~ \overline{\mathrm{d}q}\!\) describes \(a\!\)

  • \(\overline{q} ~ \mathrm{d}q\!\) describes \(d\!\)

  • \(q ~ \overline{\mathrm{d}q}\!\) describes \(b\!\)

  • \(q ~ \mathrm{d}q\!\) describes \(c\!\)

Table 4 exhibits the rules of inference that give the differential quality \(\mathrm{d}q\!\) its meaning in practice.


\(\text{Table 4.} ~~ \text{Differential Inference Rules}\!\)

\(\begin{matrix} \text{From} & \overline{q} & \text{and} & \overline{\mathrm{d}q} & \text{infer} & \overline{q} & \text{next.} \\[8pt] \text{From} & \overline{q} & \text{and} & \mathrm{d}q & \text{infer} & q & \text{next.} \\[8pt] \text{From} & q & \text{and} & \overline{\mathrm{d}q} & \text{infer} & q & \text{next.} \\[8pt] \text{From} & q & \text{and} & \mathrm{d}q & \text{infer} & \overline{q} & \text{next.} \end{matrix}\)


Cactus Calculus

Table 5 outlines a syntax for propositional calculus based on two types of logical connectives, both of variable \(k\!\)-ary scope.

  • A bracketed list of propositional expressions in the form \(\texttt{(} e_1, e_2, \ldots, e_{k-1}, e_k \texttt{)}\!\) indicates that exactly one of the propositions \(e_1, e_2, \ldots, e_{k-1}, e_k\!\) is false.
  • A concatenation of propositional expressions in the form \(e_1 ~ e_2 ~ \ldots ~ e_{k-1} ~ e_k\!\) indicates that all of the propositions \(e_1, e_2, \ldots, e_{k-1}, e_k\!\) are true, in other words, that their logical conjunction is true.


\(\text{Table 5.} ~~ \text{Syntax and Semantics of a Calculus for Propositional Logic}\!\)
\(\text{Expression}~\!\) \(\text{Interpretation}\!\) \(\text{Other Notations}\!\)
  \(\text{True}\!\) \(1\!\)
\(\texttt{(~)}\!\) \(\text{False}\!\) \(0\!\)
\(x\!\) \(x\!\) \(x\!\)
\(\texttt{(} x \texttt{)}\!\) \(\text{Not}~ x\!\)

\(\begin{matrix} x' \\ \tilde{x} \\ \lnot x \end{matrix}\!\)

\(x~y~z\!\) \(x ~\text{and}~ y ~\text{and}~ z\!\) \(x \land y \land z\!\)
\(\texttt{((} x \texttt{)(} y \texttt{)(} z \texttt{))}\!\) \(x ~\text{or}~ y ~\text{or}~ z\!\) \(x \lor y \lor z\!\)
\(\texttt{(} x ~ \texttt{(} y \texttt{))}\!\)

\(\begin{matrix} x ~\text{implies}~ y \\ \mathrm{If}~ x ~\text{then}~ y \end{matrix}\)

\(x \Rightarrow y\!\)
\(\texttt{(} x \texttt{,} y \texttt{)}\!\)

\(\begin{matrix} x ~\text{not equal to}~ y \\ x ~\text{exclusive or}~ y \end{matrix}\)

\(\begin{matrix} x \ne y \\ x + y \end{matrix}\)

\(\texttt{((} x \texttt{,} y \texttt{))}\!\)

\(\begin{matrix} x ~\text{is equal to}~ y \\ x ~\text{if and only if}~ y \end{matrix}\)

\(\begin{matrix} x = y \\ x \Leftrightarrow y \end{matrix}\)

\(\texttt{(} x \texttt{,} y \texttt{,} z \texttt{)}\!\)

\(\begin{matrix} \text{Just one of} \\ x, y, z \\ \text{is false}. \end{matrix}\)

\(\begin{matrix} x'y~z~ & \lor \\ x~y'z~ & \lor \\ x~y~z' & \end{matrix}\)

\(\texttt{((} x \texttt{),(} y \texttt{),(} z \texttt{))}\!\)

\(\begin{matrix} \text{Just one of} \\ x, y, z \\ \text{is true}. \\ & \\ \text{Partition all} \\ \text{into}~ x, y, z. \end{matrix}\)

\(\begin{matrix} x~y'z' & \lor \\ x'y~z' & \lor \\ x'y'z~ & \end{matrix}\)

\(\begin{matrix} \texttt{((} x \texttt{,} y \texttt{),} z \texttt{)} \\ & \\ \texttt{(} x \texttt{,(} y \texttt{,} z \texttt{))} \end{matrix}\!\)

\(\begin{matrix} \text{Oddly many of} \\ x, y, z \\ \text{are true}. \end{matrix}\!\)

\(x + y + z\!\)


\(\begin{matrix} x~y~z~ & \lor \\ x~y'z' & \lor \\ x'y~z' & \lor \\ x'y'z~ & \end{matrix}\!\)

\(\texttt{(} w \texttt{,(} x \texttt{),(} y \texttt{),(} z \texttt{))}\!\)

\(\begin{matrix} \text{Partition}~ w \\ \text{into}~ x, y, z. \\ & \\ \text{Genus}~ w ~\text{comprises} \\ \text{species}~ x, y, z. \end{matrix}\)

\(\begin{matrix} w'x'y'z' & \lor \\ w~x~y'z' & \lor \\ w~x'y~z' & \lor \\ w~x'y'z~ & \end{matrix}\)


All other propositional connectives can be obtained through combinations of these two forms. Strictly speaking, the concatenation form is dispensable in light of the bracket form, but it is convenient to maintain it as an abbreviation for more complicated bracket expressions. While working with expressions solely in propositional calculus, it is easiest to use plain parentheses for logical connectives. In contexts where parentheses are needed for other purposes “teletype” parentheses \(\texttt{(} \ldots \texttt{)}\!\) or barred parentheses \((\!| \ldots |\!)\) may be used for logical operators.

The briefest expression for logical truth is the empty word, abstractly denoted \(\boldsymbol\varepsilon\!\) or \(\boldsymbol\lambda\!\) in formal languages, where it forms the identity element for concatenation. It may be given visible expression in this context by means of the logically equivalent form \(\texttt{((~))},\!\) or, especially if operating in an algebraic context, by a simple \(1.\!\) Also when working in an algebraic mode, the plus sign \({+}\!\) may be used for exclusive disjunction. For example, we have the following paraphrases of algebraic expressions:

\(\begin{matrix} x + y ~=~ \texttt{(} x, y \texttt{)} \\[6pt] x + y + z ~=~ \texttt{((} x, y \texttt{)}, z \texttt{)} ~=~ \texttt{(} x, \texttt{(} y, z \texttt{))} \end{matrix}\)

It is important to note that the last expressions are not equivalent to the triple bracket \(\texttt{(} x, y, z \texttt{)}.\!\)

For more information about this syntax for propositional calculus, see the entries on minimal negation operators, zeroth order logic, and Table A1 in Appendix 1.

Formal Development

The preceding discussion outlined the ideas leading to the differential extension of propositional logic. The next task is to lay out the concepts and terminology that are needed to describe various orders of differential propositional calculi.

Elementary Notions

Logical description of a universe of discourse begins with a set of logical signs. For the sake of simplicity in a first approach, assume that these logical signs are collected in the form of a finite alphabet, \(\mathfrak{A} = \{ {}^{\backprime\backprime} a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} a_n {}^{\prime\prime} \}.\!\) Each of these signs is interpreted as denoting a logical feature, for instance, a property that objects in the universe of discourse may have or a proposition about objects in the universe of discourse. Corresponding to the alphabet \(\mathfrak{A}\!\) there is then a set of logical features, \(\mathcal{A} = \{ a_1, \ldots, a_n \}.\!\)

A set of logical features, \(\mathcal{A} = \{ a_1, \ldots, a_n \},\!\) affords a basis for generating an \(n\!\)-dimensional universe of discourse, written \(A^\bullet = [ \mathcal{A} ] = [ a_1, \ldots, a_n ].\!\) It is useful to consider a universe of discourse as a categorical object that incorporates both the set of points \(A = \langle a_1, \ldots, a_n \rangle\!\) and the set of propositions \(A^\uparrow = \{ f : A \to \mathbb{B} \}\!\) that are implicit with the ordinary picture of a venn diagram on \(n\!\) features. Accordingly, the universe of discourse \(A^\bullet\!\) may be regarded as an ordered pair \((A, A^\uparrow)\!\) having the type \((\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B})),\!\) and this last type designation may be abbreviated as \(\mathbb{B}^n\ +\!\to \mathbb{B},\!\) or even more succinctly as \([ \mathbb{B}^n ].\!\) For convenience, the data type of a finite set on \(n\!\) elements may be indicated by either one of the equivalent notations, \([n]\!\) or \(\mathbf{n}.\!\)

Table 6 summarizes the notations that are needed to describe ordinary propositional calculi in a systematic fashion.


\(\text{Table 6.} ~~ \text{Propositional Calculus : Basic Notation}\!\)
\(\text{Symbol}\!\) \(\text{Notation}\!\) \(\text{Description}\!\) \(\text{Type}\!\)
\(\mathfrak{A}\!\) \(\{ {}^{\backprime\backprime} a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} a_n {}^{\prime\prime} \}\!\) \(\text{Alphabet}\!\) \([n] = \mathbf{n}\!\)
\(\mathcal{A}\!\) \(\{ a_1, \ldots, a_n \}\!\) \(\text{Basis}\!\) \([n] = \mathbf{n}\!\)
\(A_i\!\) \(\{ \texttt{(} a_i \texttt{)}, a_i \}\!\) \(\text{Dimension}~ i\!\) \(\mathbb{B}\!\)
\(A\!\)

\(\begin{matrix} \langle \mathcal{A} \rangle \\[2pt] \langle a_1, \ldots, a_n \rangle \\[2pt] \{ (a_1, \ldots, a_n) \} \\[2pt] A_1 \times \ldots \times A_n \\[2pt] \textstyle \prod_{i=1}^n A_i \end{matrix}\)

\(\begin{matrix} \text{Set of cells}, \\[2pt] \text{coordinate tuples}, \\[2pt] \text{points, or vectors} \\[2pt] \text{in the universe} \\[2pt] \text{of discourse} \end{matrix}\)

\(\mathbb{B}^n\!\)
\(A^*\!\) \((\mathrm{hom} : A \to \mathbb{B})\!\) \(\text{Linear functions}\!\) \((\mathbb{B}^n)^* \cong \mathbb{B}^n\!\)
\(A^\uparrow\!\) \((A \to \mathbb{B})\!\) \(\text{Boolean functions}\!\) \(\mathbb{B}^n \to \mathbb{B}\!\)
\(A^\bullet\!\)

\(\begin{matrix} [\mathcal{A}] \\[2pt] (A, A^\uparrow) \\[2pt] (A ~+\!\to \mathbb{B}) \\[2pt] (A, (A \to \mathbb{B})) \\[2pt] [a_1, \ldots, a_n] \end{matrix}\)

\(\begin{matrix} \text{Universe of discourse} \\[2pt] \text{based on the features} \\[2pt] \{ a_1, \ldots, a_n \} \end{matrix}\)

\(\begin{matrix} (\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B})) \\[2pt] (\mathbb{B}^n ~+\!\to \mathbb{B}) \\[2pt] [\mathbb{B}^n] \end{matrix}\)


Special Classes of Propositions

A basic proposition, coordinate proposition, or simple proposition in the universe of discourse \([a_1, \ldots, a_n]\) is one of the propositions in the set \(\{ a_1, \ldots, a_n \}.\)

Among the \(2^{2^n}\) propositions in \([a_1, \ldots, a_n]\) are several families of \(2^n\!\) propositions each that take on special forms with respect to the basis \(\{ a_1, \ldots, a_n \}.\) Three of these families are especially prominent in the present context, the linear, the positive, and the singular propositions. Each family is naturally parameterized by the coordinate \(n\!\)-tuples in \(\mathbb{B}^n\) and falls into \(n + 1\!\) ranks, with a binomial coefficient \(\tbinom{n}{k}\) giving the number of propositions that have rank or weight \(k.\!\)

  • The linear propositions, \(\{ \ell : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{\ell} \mathbb{B}),\!\) may be written as sums:

    \(\sum_{i=1}^n e_i ~=~ e_1 + \ldots + e_n ~\text{where}~ \left\{\begin{matrix} e_i = a_i \\ \text{or} \\ e_i = 0 \end{matrix}\right\} ~\text{for}~ i = 1 ~\text{to}~ n.\!\)

  • The positive propositions, \(\{ p : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{p} \mathbb{B}),\!\) may be written as products:

    \(\prod_{i=1}^n e_i ~=~ e_1 \cdot \ldots \cdot e_n ~\text{where}~ \left\{\begin{matrix} e_i = a_i \\ \text{or} \\ e_i = 1 \end{matrix}\right\} ~\text{for}~ i = 1 ~\text{to}~ n.\!\)

  • The singular propositions, \(\{ \mathbf{x} : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{s} \mathbb{B}),\!\) may be written as products:

    \(\prod_{i=1}^n e_i ~=~ e_1 \cdot \ldots \cdot e_n ~\text{where}~ \left\{\begin{matrix} e_i = a_i \\ \text{or} \\ e_i = \texttt{(} a_i \texttt{)} \end{matrix}\right\} ~\text{for}~ i = 1 ~\text{to}~ n.\!\)

In each case the rank \(k\!\) ranges from \(0\!\) to \(n\!\) and counts the number of positive appearances of the coordinate propositions \(a_1, \ldots, a_n\!\) in the resulting expression. For example, for \(n = 3,~\!\) the linear proposition of rank \(0\!\) is \(0,\!\) the positive proposition of rank \(0\!\) is \(1,\!\) and the singular proposition of rank \(0\!\) is \(\texttt{(} a_1 \texttt{)} \texttt{(} a_2 \texttt{)} \texttt{(} a_3 \texttt{)}.\!\)

The basic propositions \(a_i : \mathbb{B}^n \to \mathbb{B}\!\) are both linear and positive. So these two kinds of propositions, the linear and the positive, may be viewed as two different ways of generalizing the class of basic propositions.

Finally, it is important to note that all of the above distinctions are relative to the choice of a particular logical basis \(\mathcal{A} = \{ a_1, \ldots, a_n \}.\!\) For example, a singular proposition with respect to the basis \(\mathcal{A}\!\) will not remain singular if \(\mathcal{A}\!\) is extended by a number of new and independent features. Even if one keeps to the original set of pairwise options \(\{ a_i \} \cup \{ \texttt{(} a_i \texttt{)} \}\!\) to pick out a new basis, the sets of linear propositions and positive propositions are both determined by the choice of basic propositions, and this whole determination is tantamount to the purely conventional choice of a cell as origin.

Differential Extensions

An initial universe of discourse, \(A^\bullet,\) supplies the groundwork for any number of further extensions, beginning with the first order differential extension, \(\mathrm{E}A^\bullet.\) The construction of \(\mathrm{E}A^\bullet\) can be described in the following stages:

  • The initial alphabet, \(\mathfrak{A} = \{ {}^{\backprime\backprime} a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} a_n {}^{\prime\prime} \},\!\) is extended by a first order differential alphabet, \(\mathrm{d}\mathfrak{A} = \{ {}^{\backprime\backprime} \mathrm{d}a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} \mathrm{d}a_n {}^{\prime\prime} \},\!\) resulting in a first order extended alphabet, \(\mathrm{E}\mathfrak{A},\) defined as follows:

    \(\mathrm{E}\mathfrak{A} ~=~ \mathfrak{A} ~\cup~ \mathrm{d}\mathfrak{A} ~=~ \{ {}^{\backprime\backprime} a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} a_n {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{d}a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} \mathrm{d}a_n {}^{\prime\prime} \}.\!\)

  • The initial basis, \(\mathcal{A} = \{ a_1, \ldots, a_n \},\!\) is extended by a first order differential basis, \(\mathrm{d}\mathcal{A} = \{ \mathrm{d}a_1, \ldots, \mathrm{d}a_n \},\!\) resulting in a first order extended basis, \(\mathrm{E}\mathcal{A},\!\) defined as follows:

    \(\mathrm{E}\mathcal{A} ~=~ \mathcal{A} ~\cup~ \mathrm{d}\mathcal{A} ~=~ \{ a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \}.\!\)

  • The initial space, \(A = \langle a_1, \ldots, a_n \rangle,\!\) is extended by a first order differential space or tangent space, \(\mathrm{d}A = \langle \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle,\!\) at each point of \(A,\!\) resulting in a first order extended space or tangent bundle space, \(\mathrm{E}A,\!\) defined as follows:

    \(\mathrm{E}A ~=~ A ~\times~ \mathrm{d}A ~=~ \langle \mathrm{E}\mathcal{A} \rangle ~=~ \langle \mathcal{A} \cup \mathrm{d}\mathcal{A} \rangle ~=~ \langle a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle.\!\)

  • Finally, the initial universe, \(A^\bullet = [ a_1, \ldots, a_n ],\!\) is extended by a first order differential universe or tangent universe, \(\mathrm{d}A^\bullet = [ \mathrm{d}a_1, \ldots, \mathrm{d}a_n ],\!\) at each point of \(A^\bullet,\!\) resulting in a first order extended universe or tangent bundle universe, \(\mathrm{E}A^\bullet,\!\) defined as follows:

    \(\mathrm{E}A^\bullet ~=~ [ \mathrm{E}\mathcal{A} ] ~=~ [ \mathcal{A} ~\cup~ \mathrm{d}\mathcal{A} ] ~=~ [ a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n ].\!\)

    This gives \(\mathrm{E}A^\bullet\!\) the type:

    \([ \mathbb{B}^n \times \mathbb{D}^n ] ~=~ (\mathbb{B}^n \times \mathbb{D}^n\ +\!\!\to \mathbb{B}) ~=~ (\mathbb{B}^n \times \mathbb{D}^n, \mathbb{B}^n \times \mathbb{D}^n \to \mathbb{B}).\!\)

A proposition in a differential extension of a universe of discourse is called a differential proposition and forms the analogue of a system of differential equations in ordinary calculus. With these constructions, the first order extended universe \(\mathrm{E}A^\bullet\) and the first order differential proposition \(f : \mathrm{E}A \to \mathbb{B},\) we have arrived, in concept at least, at the foothills of differential logic.

Table 7 summarizes the notations that are needed to describe the first order differential extensions of propositional calculi in a systematic manner.


\(\text{Table 7.} ~~ \text{Differential Extension : Basic Notation}\!\)
\(\text{Symbol}\!\) \(\text{Notation}\!\) \(\text{Description}\!\) \(\text{Type}\!\)
\(\mathrm{d}\mathfrak{A}\!\) \(\{ {}^{\backprime\backprime} \mathrm{d}a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} \mathrm{d}a_n {}^{\prime\prime} \}\!\)

\(\begin{matrix} \text{Alphabet of} \\[2pt] \text{differential symbols} \end{matrix}\)

\([n] = \mathbf{n}\!\)
\(\mathrm{d}\mathcal{A}\!\) \(\{ \mathrm{d}a_1, \ldots, \mathrm{d}a_n \}\!\)

\(\begin{matrix} \text{Basis of} \\[2pt] \text{differential features} \end{matrix}\)

\([n] = \mathbf{n}\!\)
\(\mathrm{d}A_i\!\) \(\{ \texttt{(} \mathrm{d}a_i \texttt{)}, \mathrm{d}a_i \}\!\) \(\text{Differential dimension}~ i\!\) \(\mathbb{D}\!\)
\(\mathrm{d}A\!\)

\(\begin{matrix} \langle \mathrm{d}\mathcal{A} \rangle \\[2pt] \langle \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle \\[2pt] \{ (\mathrm{d}a_1, \ldots, \mathrm{d}a_n) \} \\[2pt] \mathrm{d}A_1 \times \ldots \times \mathrm{d}A_n \\[2pt] \textstyle \prod_i \mathrm{d}A_i \end{matrix}\)

\(\begin{matrix} \text{Tangent space at a point:} \\[2pt] \text{Set of changes, motions,} \\[2pt] \text{steps, tangent vectors} \\[2pt] \text{at a point} \end{matrix}\)

\(\mathbb{D}^n\!\)
\(\mathrm{d}A^*\!\) \((\mathrm{hom} : \mathrm{d}A \to \mathbb{B})\!\) \(\text{Linear functions on}~ \mathrm{d}A\!\) \((\mathbb{D}^n)^* \cong \mathbb{D}^n\!\)
\(\mathrm{d}A^\uparrow\!\) \((\mathrm{d}A \to \mathbb{B})\!\) \(\text{Boolean functions on}~ \mathrm{d}A\!\) \(\mathbb{D}^n \to \mathbb{B}\!\)
\(\mathrm{d}A^\bullet\!\)

\(\begin{matrix} [\mathrm{d}\mathcal{A}] \\[2pt] (\mathrm{d}A, \mathrm{d}A^\uparrow) \\[2pt] (\mathrm{d}A ~+\!\to \mathbb{B}) \\[2pt] (\mathrm{d}A, (\mathrm{d}A \to \mathbb{B})) \\[2pt] [\mathrm{d}a_1, \ldots, \mathrm{d}a_n] \end{matrix}\)

\(\begin{matrix} \text{Tangent universe at a point of}~ A^\bullet, \\[2pt] \text{based on the tangent features} \\[2pt] \{ \mathrm{d}a_1, \ldots, \mathrm{d}a_n \} \end{matrix}\)

\(\begin{matrix} (\mathbb{D}^n, (\mathbb{D}^n \to \mathbb{B})) \\[2pt] (\mathbb{D}^n ~+\!\to \mathbb{B}) \\[2pt] [\mathbb{D}^n] \end{matrix}\)


…

Appendices

Appendix 1. Propositional Forms and Differential Expansions

Table A1. Propositional Forms on Two Variables


\(\text{Table A1.} ~~ \text{Propositional Forms on Two Variables}\!\)
\(\begin{matrix}\mathcal{L}_1\\\text{Decimal}\\\text{Index}\end{matrix}\) \(\begin{matrix}\mathcal{L}_2\\\text{Binary}\\\text{Index}\end{matrix}\) \(\begin{matrix}\mathcal{L}_3\\\text{Truth}\\\text{Table}\end{matrix}\) \(\begin{matrix}\mathcal{L}_4\\\text{Cactus}\\\text{Language}\end{matrix}\) \(\begin{matrix}\mathcal{L}_5\\\text{English}\\\text{Paraphrase}\end{matrix}\) \(\begin{matrix}\mathcal{L}_6\\\text{Conventional}\\\text{Formula}\end{matrix}\)
  \(x\colon\!\) \(1~1~0~0\!\)      
  \(y\colon\!\) \(1~0~1~0\!\)      

\(\begin{matrix} f_{0}\\f_{1}\\f_{2}\\f_{3}\\f_{4}\\f_{5}\\f_{6}\\f_{7} \end{matrix}\)

\(\begin{matrix} f_{0000}\\f_{0001}\\f_{0010}\\f_{0011}\\f_{0100}\\f_{0101}\\f_{0110}\\f_{0111} \end{matrix}\)

\(\begin{matrix} 0~0~0~0\\0~0~0~1\\0~0~1~0\\0~0~1~1\\0~1~0~0\\0~1~0~1\\0~1~1~0\\0~1~1~1 \end{matrix}\!\)

\(\begin{matrix} \texttt{(~)} \\ \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{(} x \texttt{)~ ~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~ ~(} y \texttt{)} \\ \texttt{(} x \texttt{,~} y \texttt{)} \\ \texttt{(} x \texttt{~~} y \texttt{)} \end{matrix}\)

\(\begin{matrix} \text{false} \\ \text{neither}~ x ~\text{nor}~ y \\ y ~\text{without}~ x \\ \text{not}~ x \\ x ~\text{without}~ y \\ \text{not}~ y \\ x ~\text{not equal to}~ y \\ \text{not both}~ x ~\text{and}~ y \end{matrix}\)

\(\begin{matrix} 0 \\ \lnot x \land \lnot y \\ \lnot x \land y \\ \lnot x \\ x \land \lnot y \\ \lnot y \\ x \ne y \\ \lnot x \lor \lnot y \end{matrix}\)

\(\begin{matrix} f_{8}\\f_{9}\\f_{10}\\f_{11}\\f_{12}\\f_{13}\\f_{14}\\f_{15} \end{matrix}\)

\(\begin{matrix} f_{1000}\\f_{1001}\\f_{1010}\\f_{1011}\\f_{1100}\\f_{1101}\\f_{1110}\\f_{1111} \end{matrix}\!\)

\(\begin{matrix} 1~0~0~0\\1~0~0~1\\1~0~1~0\\1~0~1~1\\1~1~0~0\\1~1~0~1\\1~1~1~0\\1~1~1~1 \end{matrix}\)

\(\begin{matrix} \texttt{~~} x \texttt{~~} y \texttt{~~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \\ \texttt{~ ~ ~} y \texttt{~~} \\ \texttt{~(} x \texttt{~(} y \texttt{))} \\ \texttt{~~} x \texttt{~ ~ ~} \\ \texttt{((} x \texttt{)~} y \texttt{)~} \\ \texttt{((} x \texttt{)(} y \texttt{))} \\ \texttt{((~))} \end{matrix}\)

\(\begin{matrix} x ~\text{and}~ y \\ x ~\text{equal to}~ y \\ y \\ \text{not}~ x ~\text{without}~ y \\ x \\ \text{not}~ y ~\text{without}~ x \\ x ~\text{or}~ y \\ \text{true} \end{matrix}\)

\(\begin{matrix} x \land y \\ x = y \\ y \\ x \Rightarrow y \\ x \\ x \Leftarrow y \\ x \lor y \\ 1 \end{matrix}\)


Table A2. Propositional Forms on Two Variables


\(\text{Table A2.} ~~ \text{Propositional Forms on Two Variables}\!\)
\(\begin{matrix}\mathcal{L}_1\\\text{Decimal}\\\text{Index}\end{matrix}\) \(\begin{matrix}\mathcal{L}_2\\\text{Binary}\\\text{Index}\end{matrix}\) \(\begin{matrix}\mathcal{L}_3\\\text{Truth}\\\text{Table}\end{matrix}\) \(\begin{matrix}\mathcal{L}_4\\\text{Cactus}\\\text{Language}\end{matrix}\) \(\begin{matrix}\mathcal{L}_5\\\text{English}\\\text{Paraphrase}\end{matrix}\) \(\begin{matrix}\mathcal{L}_6\\\text{Conventional}\\\text{Formula}\end{matrix}\)
  \(x\colon\!\) \(1~1~0~0\!\)      
  \(y\colon\!\) \(1~0~1~0\!\)      
\(f_{0}\!\) \(f_{0000}\!\) \(0~0~0~0\) \(\texttt{(~)}\!\) \(\text{false}\!\) \(0\!\)

\(\begin{matrix} f_{1}\\f_{2}\\f_{4}\\f_{8} \end{matrix}\)

\(\begin{matrix} f_{0001}\\f_{0010}\\f_{0100}\\f_{1000} \end{matrix}\)

\(\begin{matrix} 0~0~0~1\\0~0~1~0\\0~1~0~0\\1~0~0~0 \end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \text{neither}~ x ~\text{nor}~ y \\ y ~\text{without}~ x \\ x ~\text{without}~ y \\ x ~\text{and}~ y \end{matrix}\)

\(\begin{matrix} \lnot x \land \lnot y \\ \lnot x \land y \\ x \land \lnot y \\ x \land y \end{matrix}\)

\(\begin{matrix} f_{3}\\f_{12} \end{matrix}\)

\(\begin{matrix} f_{0011}\\f_{1100} \end{matrix}\)

\(\begin{matrix} 0~0~1~1\\1~1~0~0 \end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\)

\(\begin{matrix} \text{not}~ x \\ x \end{matrix}\!\)

\(\begin{matrix} \lnot x \\ x \end{matrix}\)

\(\begin{matrix} f_{6}\\f_{9} \end{matrix}\)

\(\begin{matrix} f_{0110}\\f_{1001} \end{matrix}\!\)

\(\begin{matrix} 0~1~1~0\\1~0~0~1 \end{matrix}\)

\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} x ~\text{not equal to}~ y \\ x ~\text{equal to}~ y \end{matrix}\)

\(\begin{matrix} x \ne y \\ x = y \end{matrix}\)

\(\begin{matrix} f_{5}\\f_{10} \end{matrix}\)

\(\begin{matrix} f_{0101}\\f_{1010} \end{matrix}\)

\(\begin{matrix} 0~1~0~1\\1~0~1~0 \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \text{not}~ y \\ y \end{matrix}\)

\(\begin{matrix} \lnot y \\ y \end{matrix}\)

\(\begin{matrix} f_{7}\\f_{11}\\f_{13}\\f_{14} \end{matrix}\)

\(\begin{matrix} f_{0111}\\f_{1011}\\f_{1101}\\f_{1110} \end{matrix}\)

\(\begin{matrix} 0~1~1~1\\1~0~1~1\\1~1~0~1\\1~1~1~0 \end{matrix}\)

\(\begin{matrix} \texttt{~(} x \texttt{~~} y \texttt{)~} \\ \texttt{~(} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{)~} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \text{not both}~ x ~\text{and}~ y \\ \text{not}~ x ~\text{without}~ y \\ \text{not}~ y ~\text{without}~ x \\ x ~\text{or}~ y \end{matrix}\)

\(\begin{matrix} \lnot x \lor \lnot y \\ x \Rightarrow y \\ x \Leftarrow y \\ x \lor y \end{matrix}\)

\(f_{15}\!\) \(f_{1111}\!\) \(1~1~1~1\!\) \(\texttt{((~))}\!\) \(\text{true}\!\) \(1\!\)


Table A3. Ef Expanded Over Differential Features


\(\text{Table A3.} ~~ \mathrm{E}f ~\text{Expanded Over Differential Features}~ \{ \mathrm{d}x, \mathrm{d}y \}\!\)
  \(f\!\)

\(\begin{matrix}\mathrm{T}_{11}f\\\mathrm{E}f|_{\mathrm{d}x ~ \mathrm{d}y}\end{matrix}\)

\(\begin{matrix}\mathrm{T}_{10}f\\\mathrm{E}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}}\end{matrix}\)

\(\begin{matrix}\mathrm{T}_{01}f\\\mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y}\end{matrix}\)

\(\begin{matrix}\mathrm{T}_{00}f\\\mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}}\end{matrix}\)

\(f_{0}\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)

\(\begin{matrix} f_{1}\\f_{2}\\f_{4}\\f_{8} \end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{~} x \texttt{~~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{(} x \texttt{)(} y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \\ \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \end{matrix}\!\)

\(\begin{matrix} \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} f_{3}\\f_{12} \end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{~} x \texttt{~} \\ \texttt{(} x \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{~} x \texttt{~} \\ \texttt{(} x \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\)

\(\begin{matrix} f_{6}\\f_{9} \end{matrix}\)

\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{((} x \texttt{,~} y \texttt{))} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\)

\(\begin{matrix} \texttt{((} x \texttt{,~} y \texttt{))} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\)

\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} f_{5}\\f_{10} \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{~} y \texttt{~} \\ \texttt{(} y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{~} y \texttt{~} \\ \texttt{(} y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} f_{7}\\f_{11}\\f_{13}\\f_{14} \end{matrix}\)

\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{((} x \texttt{)(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{(~} x \texttt{~~} y \texttt{~)} \end{matrix}\)

\(\begin{matrix} \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \\ \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \end{matrix}\!\)

\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\)

\(f_{15}\!\) \(1\!\) \(1\!\) \(1\!\) \(1\!\) \(1\!\)
\(\text{Fixed Point Total}\!\) \(4\!\) \(4\!\) \(4\!\) \(16\!\)


Table A4. Df Expanded Over Differential Features


\(\text{Table A4.} ~~ \mathrm{D}f ~\text{Expanded Over Differential Features}~ \{ \mathrm{d}x, \mathrm{d}y \}\!\)
  \(f\!\)

\(\mathrm{D}f|_{\mathrm{d}x ~ \mathrm{d}y}\!\)

\(\mathrm{D}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}}\!\)

\(\mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y}~\!\)

\(\mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}}\!\)

\(f_{0}\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)

\(\begin{matrix} f_{1}\\f_{2}\\f_{4}\\f_{8} \end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{((} x \texttt{,~} y \texttt{))} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ y \\ \texttt{(} y \texttt{)} \\ y \end{matrix}\!\)

\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{(} x \texttt{)} \\ x \\ x \end{matrix}\)

\(\begin{matrix}0\\0\\0\\0\end{matrix}\)

\(\begin{matrix}f_{3}\\f_{12}\end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)} \\ x \end{matrix}\)

\(\begin{matrix}1\\1\end{matrix}\)

\(\begin{matrix}1\\1\end{matrix}\)

\(\begin{matrix}0\\0\end{matrix}\)

\(\begin{matrix}0\\0\end{matrix}\)

\(\begin{matrix}f_{6}\\f_{9}\end{matrix}\)

\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix}0\\0\end{matrix}\)

\(\begin{matrix}1\\1\end{matrix}\)

\(\begin{matrix}1\\1\end{matrix}\)

\(\begin{matrix}0\\0\end{matrix}\)

\(\begin{matrix}f_{5}\\f_{10}\end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\)

\(\begin{matrix}1\\1\end{matrix}\)

\(\begin{matrix}0\\0\end{matrix}\)

\(\begin{matrix}1\\1\end{matrix}\)

\(\begin{matrix}0\\0\end{matrix}\)

\(\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}\)

\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{((} x \texttt{,~} y \texttt{))} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} y \\ \texttt{(} y \texttt{)} \\ y \\ \texttt{(} y \texttt{)} \end{matrix}\)

\(\begin{matrix} x \\ x \\ \texttt{(} x \texttt{)} \\ \texttt{(} x \texttt{)} \end{matrix}\)

\(\begin{matrix}0\\0\\0\\0\end{matrix}\)

\(f_{15}\!\) \(1\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)


Table A5. Ef Expanded Over Ordinary Features


\(\text{Table A5.} ~~ \mathrm{E}f ~\text{Expanded Over Ordinary Features}~ \{ x, y \}\!\)
  \(f\!\)

\(\mathrm{E}f|_{xy}\!\)

\(\mathrm{E}f|_{x \texttt{(} y \texttt{)}}\!\)

\(\mathrm{E}f|_{\texttt{(} x \texttt{)} y}\!\)

\(\mathrm{E}f|_{\texttt{(} x \texttt{)(} y \texttt{)}}\!\)

\(f_{0}\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)

\(\begin{matrix} f_{1}\\f_{2}\\f_{4}\\f_{8} \end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \end{matrix}\!\)

\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \end{matrix}\)

\(\begin{matrix} f_{3}\\f_{12} \end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~} \\ \texttt{(} \mathrm{d}x \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~} \\ \texttt{(} \mathrm{d}x \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~} \end{matrix}\)

\(\begin{matrix} f_{6}\\f_{9} \end{matrix}\)

\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~} \\ \texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))} \\ \texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~} \end{matrix}\)

\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))} \\ \texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~} \end{matrix}\)

\(\begin{matrix} \texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~} \\ \texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))} \end{matrix}\)

\(\begin{matrix} f_{5}\\f_{10} \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{~} \mathrm{d}y \texttt{~} \\ \texttt{(} \mathrm{d}y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{~} \mathrm{d}y \texttt{~} \\ \texttt{(} \mathrm{d}y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}y \texttt{~} \end{matrix}\)

\(\begin{matrix} f_{7}\\f_{11}\\f_{13}\\f_{14} \end{matrix}\)

\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)} \\ \texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))} \\ \texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)} \end{matrix}\)

\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)} \\ \texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))} \\ \texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)} \end{matrix}\!\)

\(\begin{matrix} \texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)} \\ \texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))} \\ \texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \end{matrix}\)

\(f_{15}\!\) \(1\!\) \(1\!\) \(1\!\) \(1\!\) \(1\!\)


Table A6. Df Expanded Over Ordinary Features


\(\text{Table A6.} ~~ \mathrm{D}f ~\text{Expanded Over Ordinary Features}~ \{ x, y \}\!\)
  \(f\!\)

\(\mathrm{D}f|_{xy}\!\)

\(\mathrm{D}f|_{x \texttt{(} y \texttt{)}}\!\)

\(\mathrm{D}f|_{\texttt{(} x \texttt{)} y}\!\)

\(\mathrm{D}f|_{\texttt{(} x \texttt{)(} y \texttt{)}}\!\)

\(f_{0}\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)
\(\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \end{matrix}\!\)

\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \end{matrix}\)

\(\begin{matrix}f_{3}\\f_{12}\end{matrix}\)

\(\begin{matrix}\texttt{(} x \texttt{)}\\\texttt{~} x \texttt{~}\end{matrix}\)

\(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\)

\(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\)

\(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\)

\(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\)

\(\begin{matrix}f_{6}\\f_{9}\end{matrix}\)

\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \end{matrix}\)

\(\begin{matrix}f_{5}\\f_{10}\end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\)

\(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\)

\(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\)

\(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\)

\(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\)

\(\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}\)

\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \end{matrix}\!\)

\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \end{matrix}\)

\(f_{15}\!\) \(1\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)


Appendix 2. Differential Forms

The actions of the difference operator \(\mathrm{D}\!\) and the tangent operator \(\mathrm{d}\!\) on the 16 bivariate propositions are shown in Tables A7 and A8.

Table A7 expands the differential forms that result over a logical basis:

\(\{~ \texttt{(}\mathrm{d}x\texttt{)(}\mathrm{d}y\texttt{)}, ~\mathrm{d}x~\texttt{(}\mathrm{d}y\texttt{)}, ~\texttt{(}\mathrm{d}x\texttt{)}~\mathrm{d}y, ~\mathrm{d}x~\mathrm{d}y ~\}.\!\)

This set consists of the singular propositions in the first order differential variables, indicating mutually exclusive and exhaustive cells of the tangent universe of discourse. Accordingly, this set of differential propositions may also be referred to as the cell-basis, point-basis, or singular differential basis. In this setting it is frequently convenient to use the following abbreviations:

\(\partial x ~=~ \mathrm{d}x~\texttt{(}\mathrm{d}y\texttt{)}\!\)     and     \(\partial y ~=~ \texttt{(}\mathrm{d}x\texttt{)}~\mathrm{d}y.\!\)

Table A8 expands the differential forms that result over an algebraic basis:

\(\{~ 1, ~\mathrm{d}x, ~\mathrm{d}y, ~\mathrm{d}x~\mathrm{d}y ~\}.\!\)

This set consists of the positive propositions in the first order differential variables, indicating overlapping positive regions of the tangent universe of discourse. Accordingly, this set of differential propositions may also be referred to as the positive differential basis.

Table A7. Differential Forms Expanded on a Logical Basis


\(\text{Table A7.} ~~ \text{Differential Forms Expanded on a Logical Basis}\!\)
  \(f\!\) \(\mathrm{D}f~\!\) \(\mathrm{d}f~\!\)
\(f_{0}\!\) \(\texttt{(~)}\!\) \(0\!\) \(0\!\)
\(\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y \\ y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y \\ \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & x & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y \\ y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & x & \texttt{(} \mathrm{d}x) ~ \mathrm{d}y & + & \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} ~\partial x & + & \texttt{(} x \texttt{)} ~\partial y \\ \texttt{~} y \texttt{~} ~\partial x & + & \texttt{(} x \texttt{)} ~\partial y \\ \texttt{(} y \texttt{)} ~\partial x & + & \texttt{~} x \texttt{~} ~\partial y \\ \texttt{~} y \texttt{~} ~\partial x & + & \texttt{~} x \texttt{~} ~\partial y \end{matrix}\)

\(\begin{matrix}f_{3}\\f_{12}\end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\)

\(\begin{matrix} \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \mathrm{d}x ~ \mathrm{d}y \\ \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \mathrm{d}x ~ \mathrm{d}y \end{matrix}\!\)

\(\begin{matrix} \partial x \\ \partial x \end{matrix}\)

\(\begin{matrix}f_{6}\\f_{9}\end{matrix}\)

\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y \\ \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \partial x & + & \partial y \\ \partial x & + & \partial y \end{matrix}\)

\(\begin{matrix}f_{5}\\f_{10}\end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \mathrm{d}x ~ \mathrm{d}y \\ \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \mathrm{d}x ~ \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \partial y \\ \partial y \end{matrix}\)

\(\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}\)

\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\)

\(\begin{matrix} y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & x & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y \\ \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & x & \texttt{(} \mathrm{d}x) ~ \mathrm{d}y & + & \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y \\ y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y \\ \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \texttt{~} y \texttt{~} ~\partial x & + & \texttt{~} x \texttt{~} ~\partial y \\ \texttt{(} y \texttt{)} ~\partial x & + & \texttt{~} x \texttt{~} ~\partial y \\ \texttt{~} y \texttt{~} ~\partial x & + & \texttt{(} x \texttt{)} ~\partial y \\ \texttt{(} y \texttt{)} ~\partial x & + & \texttt{(} x \texttt{)} ~\partial y \end{matrix}\)

\(f_{15}\!\) \(\texttt{((~))}\!\) \(0\!\) \(0\!\)


Table A8. Differential Forms Expanded on an Algebraic Basis


\(\text{Table A8.} ~~ \text{Differential Forms Expanded on an Algebraic Basis}\!\)
  \(f\!\) \(\mathrm{D}f~\!\) \(\mathrm{d}f~\!\)
\(f_{0}\!\) \(\texttt{(~)}\!\) \(0\!\) \(0\!\)
\(\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y \\ \texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y \\ \texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y \\ \texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y \\ \texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y \\ \texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y \\ \texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y \end{matrix}\)

\(\begin{matrix}f_{3}\\f_{12}\end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\)

\(\begin{matrix} \mathrm{d}x \\ \mathrm{d}x \end{matrix}\!\)

\(\begin{matrix} \mathrm{d}x \\ \mathrm{d}x \end{matrix}\)
\(\begin{matrix}f_{6}\\f_{9}\end{matrix}\)

\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \mathrm{d}x & + & \mathrm{d}y \\ \mathrm{d}x & + & \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}x & + & \mathrm{d}y \\ \mathrm{d}x & + & \mathrm{d}y \end{matrix}\)

\(\begin{matrix}f_{5}\\f_{10}\end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \mathrm{d}y \\ \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}y \\ \mathrm{d}y \end{matrix}\)

\(\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}\)

\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y \\ \texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y \\ \texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y \\ \texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y & + & \mathrm{d}x~\mathrm{d}y \end{matrix}\)

\(\begin{matrix} \texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y \\ \texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{~} x \texttt{~}~\mathrm{d}y \\ \texttt{~} y \texttt{~}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y \\ \texttt{(} y \texttt{)}~\mathrm{d}x & + & \texttt{(} x \texttt{)}~\mathrm{d}y \end{matrix}\)

\(f_{15}\!\) \(\texttt{((~))}\!\) \(0\!\) \(0\!\)


Table A9. Tangent Proposition as Pointwise Linear Approximation


\(\text{Table A9.} ~~ \text{Tangent Proposition}~ \mathrm{d}f = \text{Pointwise Linear Approximation to the Difference Map}~ \mathrm{D}f\!\)
\(f\!\)

\(\begin{matrix} \mathrm{d}f = \\[2pt] \partial_x f \cdot \mathrm{d}x ~+~ \partial_y f \cdot \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}^2\!f = \\[2pt] \partial_{xy} f \cdot \mathrm{d}x\;\mathrm{d}y \end{matrix}\)

\(\mathrm{d}f|_{x \, y}\) \(\mathrm{d}f|_{x \, \texttt{(} y \texttt{)}}\) \(\mathrm{d}f|_{\texttt{(} x \texttt{)} \, y}\) \(\mathrm{d}f|_{\texttt{(} x \texttt{)(} y \texttt{)}}\)
\(f_0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)

\(\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}\!\)

\(\begin{matrix} \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y \\ \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y \\ \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y \\ \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}x\;\mathrm{d}y \\ \mathrm{d}x\;\mathrm{d}y \\ \mathrm{d}x\;\mathrm{d}y \\ \mathrm{d}x\;\mathrm{d}y \end{matrix}\)

\(\begin{matrix}0\\\mathrm{d}x\\\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}\) \(\begin{matrix}\mathrm{d}x\\0\\\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\end{matrix}\) \(\begin{matrix}\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\\0\\\mathrm{d}x\end{matrix}\) \(\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\\\mathrm{d}x\\0\end{matrix}\)

\(\begin{matrix}f_{3}\\f_{12}\end{matrix}\)

\(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\)

\(\begin{matrix}0\\0\end{matrix}\) \(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\) \(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\) \(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\) \(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\)

\(\begin{matrix}f_{6}\\f_{9}\end{matrix}\)

\(\begin{matrix}\mathrm{d}x & + & \mathrm{d}y\\\mathrm{d}x & + & \mathrm{d}y\end{matrix}\)

\(\begin{matrix}0\\0\end{matrix}\) \(\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}\) \(\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}\) \(\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}\) \(\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}\)

\(\begin{matrix}f_{5}\\f_{10}\end{matrix}\!\)

\(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\!\)

\(\begin{matrix}0\\0\end{matrix}\) \(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\!\) \(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\!\) \(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\!\) \(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\!\)

\(\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}\)

\(\begin{matrix} \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y \\ \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y \\ \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y \\ \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y \end{matrix}\!\)

\(\begin{matrix} \mathrm{d}x\;\mathrm{d}y \\ \mathrm{d}x\;\mathrm{d}y \\ \mathrm{d}x\;\mathrm{d}y \\ \mathrm{d}x\;\mathrm{d}y \end{matrix}\) \(\begin{matrix}\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\\\mathrm{d}x\\0\end{matrix}\) \(\begin{matrix}\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\\0\\\mathrm{d}x\end{matrix}\) \(\begin{matrix}\mathrm{d}x\\0\\\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\end{matrix}\) \(\begin{matrix}0\\\mathrm{d}x\\\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\end{matrix}\)
\(f_{15}\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)


Table A10. Taylor Series Expansion Df = df + d2f


\(\text{Table A10.} ~~ \text{Taylor Series Expansion}~ {\mathrm{D}f = \mathrm{d}f + \mathrm{d}^2\!f}\!\)
\(f\!\)

\(\begin{matrix} \mathrm{D}f \\ = & \mathrm{d}f & + & \mathrm{d}^2\!f \\ = & \partial_x f \cdot \mathrm{d}x ~+~ \partial_y f \cdot \mathrm{d}y & + & \partial_{xy} f \cdot \mathrm{d}x\;\mathrm{d}y \end{matrix}\)

\(\mathrm{d}f|_{x \, y}\) \(\mathrm{d}f|_{x \, \texttt{(} y \texttt{)}}\) \(\mathrm{d}f|_{\texttt{(} x \texttt{)} \, y}\) \(\mathrm{d}f|_{\texttt{(} x \texttt{)(} y \texttt{)}}\)
\(f_0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)
\(\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \\ \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \\ \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \\ \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \end{matrix}\)

\(\begin{matrix} 0\\\mathrm{d}x\\\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}x\\0\\\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\\0\\\mathrm{d}x \end{matrix}\)

\(\begin{matrix} \mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\\\mathrm{d}x\\0 \end{matrix}\)

\(\begin{matrix}f_{3}\\f_{12}\end{matrix}\)

\(\begin{matrix} \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} 0 \texttt{~} \cdot \mathrm{d}y & + & \texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \\ \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} 0 \texttt{~} \cdot \mathrm{d}y & + & \texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}x\\\mathrm{d}x \end{matrix}\)

\(\begin{matrix} \mathrm{d}x\\\mathrm{d}x \end{matrix}\)

\(\begin{matrix} \mathrm{d}x\\\mathrm{d}x \end{matrix}\)

\(\begin{matrix} \mathrm{d}x\\\mathrm{d}x \end{matrix}\)

\(\begin{matrix}f_{6}\\f_{9}\end{matrix}\)

\(\begin{matrix} \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}y & + & \texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \\ \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}y & + & \texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}x + \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y \end{matrix}\)

\(\begin{matrix}f_{5}\\f_{10}\end{matrix}\)

\(\begin{matrix} \texttt{~} 0 \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}y & + & \texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \\ \texttt{~} 0 \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}y & + & \texttt{~} 0 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}y\\\mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}y\\\mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}y\\\mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}y\\\mathrm{d}y \end{matrix}\)

\(\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}\)

\(\begin{matrix} \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \\ \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \\ \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \\ \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y & + & \texttt{~} 1 \texttt{~} \cdot \mathrm{d}x\;\mathrm{d}y \end{matrix}\)

\(\begin{matrix} \mathrm{d}x + \mathrm{d}y\\\mathrm{d}y\\\mathrm{d}x\\0 \end{matrix}\)

\(\begin{matrix} \mathrm{d}y\\\mathrm{d}x + \mathrm{d}y\\0\\\mathrm{d}x \end{matrix}\)

\(\begin{matrix} \mathrm{d}x\\0\\\mathrm{d}x + \mathrm{d}y\\\mathrm{d}y \end{matrix}\)

\(\begin{matrix} 0\\\mathrm{d}x\\\mathrm{d}y\\\mathrm{d}x + \mathrm{d}y \end{matrix}\)

\(f_{15}\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)


Table A11. Partial Differentials and Relative Differentials


\(\text{Table A11.} ~~ \text{Partial Differentials and Relative Differentials}\!\)
  \(f\!\) \(\frac{\partial f}{\partial x}\!\) \(\frac{\partial f}{\partial y}\!\)

\(\begin{matrix} \mathrm{d}f = \\[2pt] \partial_x f \cdot \mathrm{d}x ~+~ \partial_y f \cdot \mathrm{d}y \end{matrix}\)

\(\left. \frac{\partial x}{\partial y} \right| f\!\) \(\left. \frac{\partial y}{\partial x} \right| f\!\)
\(f_0\!\) \(\texttt{(~)}\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)
\(\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \\ \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \\ \texttt{~} x \texttt{~} \end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y \\ \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y \\ \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y \\ \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y \end{matrix}\)

\(\begin{matrix}\cdots\\\cdots\\\cdots\\\cdots\end{matrix}\) \(\begin{matrix}\cdots\\\cdots\\\cdots\\\cdots\end{matrix}\)
\(\begin{matrix}f_{3}\\f_{12}\end{matrix}\)

\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\)

\(\begin{matrix}1\\1\end{matrix}\) \(\begin{matrix}0\\0\end{matrix}\) \(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\) \(\begin{matrix}\cdots\\\cdots\end{matrix}\) \(\begin{matrix}\cdots\\\cdots\end{matrix}\)
\(\begin{matrix}f_{6}\\f_{9}\end{matrix}\)

\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix}1\\1\end{matrix}\) \(\begin{matrix}1\\1\end{matrix}\) \(\begin{matrix}\mathrm{d}x & + & \mathrm{d}y\\\mathrm{d}x & + & \mathrm{d}y\end{matrix}\) \(\begin{matrix}\cdots\\\cdots\end{matrix}\) \(\begin{matrix}\cdots\\\cdots\end{matrix}\)
\(\begin{matrix}f_{5}\\f_{10}\end{matrix}\)

\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\)

\(\begin{matrix}0\\0\end{matrix}\) \(\begin{matrix}1\\1\end{matrix}\) \(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\) \(\begin{matrix}\cdots\\\cdots\end{matrix}\) \(\begin{matrix}\cdots\\\cdots\end{matrix}\)
\(\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}\)

\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\)

\(\begin{matrix} \texttt{~} y \texttt{~} \\ \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \\ \texttt{(} y \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{~} x \texttt{~} \\ \texttt{~} x \texttt{~} \\ \texttt{(} x \texttt{)} \\ \texttt{(} x \texttt{)} \end{matrix}\)

\(\begin{matrix} \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y \\ \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{~} x \texttt{~} \cdot \mathrm{d}y \\ \texttt{~} y \texttt{~} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y \\ \texttt{(} y \texttt{)} \cdot \mathrm{d}x & + & \texttt{(} x \texttt{)} \cdot \mathrm{d}y \end{matrix}\)

\(\begin{matrix}\cdots\\\cdots\\\cdots\\\cdots\end{matrix}\) \(\begin{matrix}\cdots\\\cdots\\\cdots\\\cdots\end{matrix}\)
\(f_{15}\!\) \(\texttt{((~))}\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\) \(0\!\)


Table A12. Detail of Calculation for the Difference Map


\(\text{Table A12.} ~~ \text{Detail of Calculation for}~ {\mathrm{E}f + f = \mathrm{D}f}\!\)
  \(f\!\)

\(\begin{array}{cr} ~ & \mathrm{E}f|_{\mathrm{d}x ~ \mathrm{d}y} \\[4pt] + & f|_{\mathrm{d}x ~ \mathrm{d}y} \\[4pt] = & \mathrm{D}f|_{\mathrm{d}x ~ \mathrm{d}y} \end{array}\)

\(\begin{array}{cr} ~ & \mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y} \\[4pt] + & f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y} \\[4pt] = & \mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y} \end{array}\)

\(\begin{array}{cr} ~ & \mathrm{E}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}} \\[4pt] + & f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}} \\[4pt] = & \mathrm{D}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}} \end{array}\)

\(\begin{array}{cr} ~ & \mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}} \\[4pt] + & f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}} \\[4pt] = & \mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}} \end{array}\)

\(f_{0}\!\) \(0\!\) \(0 ~+~ 0 ~=~ 0\!\) \(0 ~+~ 0 ~=~ 0\!\) \(0 ~+~ 0 ~=~ 0\!\) \(0 ~+~ 0 ~=~ 0\!\)
\(f_{1}\!\)

\(\texttt{~(} x \texttt{)(} y \texttt{)~}\!\)

\(\begin{matrix} ~ & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] + & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] = & \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] = & \texttt{~~} ~ \texttt{~(} y \texttt{)~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] + & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] = & \texttt{~(} x \texttt{)~} ~ \texttt{~~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\)

\(f_{2}\!\)

\(\texttt{~(} x \texttt{)~} y \texttt{~~}\!\)

\(\begin{matrix} ~ & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] = & \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] + & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] = & \texttt{~~} ~ \texttt{~~} y \texttt{~~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] = & \texttt{~(} x \texttt{)~} ~ \texttt{~~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] + & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] = & 0 \end{matrix}\)

\(f_{4}\!\)

\(\texttt{~~} x \texttt{~(} y \texttt{)~}\!\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] + & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] = & \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] + & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] = & \texttt{~~} ~ \texttt{~(} y \texttt{)~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] + & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] = & \texttt{~~} x \texttt{~~} ~ \texttt{~~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] + & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\)

\(f_{8}\!\)

\(\texttt{~~} x \texttt{~~} y \texttt{~~}\!\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] + & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] = & \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] + & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] = & \texttt{~~} ~ \texttt{~~} y \texttt{~~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] + & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] = & \texttt{~~} x \texttt{~~} ~ \texttt{~~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] + & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] = & 0 \end{matrix}\)

\(f_{3}\!\)

\(\texttt{(} x \texttt{)}\!\)

\(\begin{matrix} ~ & x \\[4pt] + & \texttt{(} x \texttt{)} \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & x \\[4pt] + & \texttt{(} x \texttt{)} \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{(} x \texttt{)} \\[4pt] + & \texttt{(} x \texttt{)} \\[4pt] = & 0 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{(} x \texttt{)} \\[4pt] + & \texttt{(} x \texttt{)} \\[4pt] = & 0 \end{matrix}\)

\(f_{12}\!\)

\(x\!\)

\(\begin{matrix} ~ & \texttt{(} x \texttt{)} \\[4pt] + & x \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{(} x \texttt{)} \\[4pt] + & x \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & x \\[4pt] + & x \\[4pt] = & 0 \end{matrix}\)

\(\begin{matrix} ~ & x \\[4pt] + & x \\[4pt] = & 0 \end{matrix}\)

\(f_{6}\!\)

\(\texttt{~(} x \texttt{,~} y \texttt{)~}\!\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\)

\(f_{9}\!\)

\(\texttt{((} x \texttt{,~} y \texttt{))}\!\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] = & 0 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] = & 0 \end{matrix}\)

\(f_{5}\!\)

\(\texttt{(} y \texttt{)}\!\)

\(\begin{matrix} ~ & y \\[4pt] + & \texttt{(} y \texttt{)} \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{(} y \texttt{)} \\[4pt] + & \texttt{(} y \texttt{)} \\[4pt] = & 0 \end{matrix}\)

\(\begin{matrix} ~ & y \\[4pt] + & \texttt{(} y \texttt{)} \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{(} y \texttt{)} \\[4pt] + & \texttt{(} y \texttt{)} \\[4pt] = & 0 \end{matrix}\)

\(f_{10}\!\)

\(y\!\)

\(\begin{matrix} ~ & \texttt{(} y \texttt{)} \\[4pt] + & y \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & y \\[4pt] + & y \\[4pt] = & 0 \end{matrix}\)

\(\begin{matrix} ~ & \texttt{(} y \texttt{)} \\[4pt] + & y \\[4pt] = & 1 \end{matrix}\)

\(\begin{matrix} ~ & y \\[4pt] + & y \\[4pt] = & 0 \end{matrix}\)

\(f_{7}\!\)

\(\texttt{~(} x \texttt{~~} y \texttt{)~}\!\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] = & \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] = & \texttt{~~} ~ \texttt{~~} y \texttt{~~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] = & \texttt{~~} x \texttt{~~} ~ \texttt{~~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\)

\(f_{11}\!\)

\(\texttt{~(} x \texttt{~(} y \texttt{))}\!\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] = & \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] = & \texttt{~~} ~ \texttt{~(} y \texttt{)~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] = & \texttt{~~} x \texttt{~~} ~ \texttt{~~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] = & 0 \end{matrix}\)

\(f_{13}\!\)

\(\texttt{((} x \texttt{)~} y \texttt{)~}\!\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] = & \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] = & \texttt{~~} ~ \texttt{~~} y \texttt{~~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] = & \texttt{~(} x \texttt{)~} ~ \texttt{~~} \end{matrix}\!\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\)

\(f_{14}\!\)

\(\texttt{((} x \texttt{)(} y \texttt{))}\!\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] = & \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] = & \texttt{~~} ~ \texttt{~(} y \texttt{)~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] = & \texttt{~(} x \texttt{)~} ~ \texttt{~~} \end{matrix}\)

\(\begin{matrix} ~ & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] = & 0 \end{matrix}\)

\(f_{15}\!\) \(1\!\) \(1 ~+~ 1 ~=~ 0\!\) \(1 ~+~ 1 ~=~ 0\!\) \(1 ~+~ 1 ~=~ 0\!\) \(1 ~+~ 1 ~=~ 0\!\)


Appendix 3. Computational Details

Operator Maps for the Logical Conjunction f8(u, v)

Computation of εf8


\(\text{Table F8.1} ~~ \text{Computation of}~ \boldsymbol\varepsilon f_{8}~\!\)

\(\begin{array}{*{10}{l}} \boldsymbol\varepsilon f_{8} & = && f_{8}(u, v) \\[4pt] & = && uv \\[4pt] & = && uv \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & uv \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v & + & uv \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)} & + & uv \cdot \mathrm{d}u ~ \mathrm{d}v \\[20pt] \boldsymbol\varepsilon f_{8} & = && uv \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} \\[4pt] && + & uv \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} \\[4pt] && + & uv \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} \\[4pt] && + & uv \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} \end{array}\!\)


Computation of Ef8


\(\text{Table F8.2-i} ~~ \text{Computation of}~ \mathrm{E}f_{8} ~\text{(Method 1)}\!\)

\(\begin{array}{*{9}{l}} \mathrm{E}f_{8} & = & f_{8}(u + \mathrm{d}u, v + \mathrm{d}v) \\[4pt] & = & \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)(} v \texttt{,} \mathrm{d}v \texttt{)} \\[4pt] & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot f_{8}(\texttt{(} \mathrm{d}u \texttt{)}, \texttt{(} \mathrm{d}v \texttt{)}) & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot f_{8}(\texttt{(} \mathrm{d}u \texttt{)}, \mathrm{d}v) & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot f_{8}(\mathrm{d}u, \texttt{(} \mathrm{d}v \texttt{)}) & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot f_{8}(\mathrm{d}u, \mathrm{d}v) \\[4pt] & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \\[20pt] \mathrm{E}f_{8} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} \\[4pt] &&& + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v \\[4pt] &&&&& + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)} \\[4pt] &&&&&&& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \end{array}\!\)


\(\text{Table F8.2-ii} ~~ \text{Computation of}~ \mathrm{E}f_{8} ~\text{(Method 2)}\!\)

\(\begin{array}{*{9}{c}} \mathrm{E}f_{8} & = & (u + \mathrm{d}u) \cdot (v + \mathrm{d}v) \\[6pt] & = & u \cdot v & + & u \cdot \mathrm{d}v & + & v \cdot \mathrm{d}u & + & \mathrm{d}u \cdot \mathrm{d}v \\[6pt] \mathrm{E}f_{8} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \end{array}\!\)


Computation of Df8


\(\text{Table F8.3-i} ~~ \text{Computation of}~ \mathrm{D}f_{8} ~\text{(Method 1)}\!\)

\(\begin{array}{*{10}{l}} \mathrm{D}f_{8} & = && \mathrm{E}f_{8} & + & \boldsymbol\varepsilon f_{8} \\[4pt] & = && f_{8}(u + \mathrm{d}u, v + \mathrm{d}v) & + & f_{8}(u, v) \\[4pt] & = && \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)(} v \texttt{,} \mathrm{d}v \texttt{)} & + & uv \\[20pt] \mathrm{D}f_{8} & = && 0 & + & 0 & + & 0 & + & 0 \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~~} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & 0 & + & 0 \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)~} & + & 0 & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & 0 \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~~} & + & 0 & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~} \mathrm{d}v \texttt{~} \\[20pt] \mathrm{D}f_{8} & = && \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~} \mathrm{d}v \texttt{~} \end{array}\!\)


\(\text{Table F8.3-ii} ~~ \text{Computation of}~ \mathrm{D}f_{8} ~\text{(Method 2)}\!\)

\(\begin{array}{*{9}{l}} \mathrm{D}f_{8} & = & \boldsymbol\varepsilon f_{8} & + & \mathrm{E}f_{8} \\[6pt] & = & f_{8}(u, v) & + & f_{8}(u + \mathrm{d}u, v + \mathrm{d}v) \\[6pt] & = & uv & + & \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)(} v \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] & = & 0 & + & u \cdot \mathrm{d}v & + & v \cdot \mathrm{d}u & + & \mathrm{d}u ~ \mathrm{d}v \\[6pt] \mathrm{D}f_{8} & = & 0 & + & u \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v & + & v \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{((} u \texttt{,} v \texttt{))} \cdot \mathrm{d}u ~ \mathrm{d}v \end{array}\)


\(\text{Table F8.3-iii} ~~ \text{Computation of}~ \mathrm{D}f_{8} ~\text{(Method 3)}\!\)

\(\begin{array}{c*{9}{l}} \mathrm{D}f_{8} & = & \boldsymbol\varepsilon f_{8} ~+~ \mathrm{E}f_{8} \\[20pt] \boldsymbol\varepsilon f_{8} & = & u \,\cdot\, v \,\cdot\, \texttt{(} \mathrm{d}u \texttt{)} \texttt{(} \mathrm{d}v \texttt{)} & + & u \,\cdot\, v \,\cdot\, \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & ~ u \,\cdot\, v \,\cdot\, \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & ~ u \;\cdot\; v \;\cdot\; \mathrm{d}u ~ \mathrm{d}v \\[6pt] \mathrm{E}f_{8} & = & u \,\cdot\, v \,\cdot\, \texttt{(} \mathrm{d}u \texttt{)} \texttt{(} \mathrm{d}v \texttt{)} & + & u ~ \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)} ~ v \,\cdot\, \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} \texttt{(} v \texttt{)} \cdot\, \mathrm{d}u ~ \mathrm{d}v \\[20pt] \mathrm{D}f_{8} & = & ~ ~ 0 ~~ \cdot ~ \texttt{(} \mathrm{d}u \texttt{)} \texttt{(} \mathrm{d}v \texttt{)} & + & ~ ~ u ~~ \cdot ~ \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & ~ ~ ~ v ~~ \cdot ~ \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{((} u \texttt{,} v \texttt{))} \cdot \mathrm{d}u ~ \mathrm{d}v \end{array}\!\)

Computation of df8


\(\text{Table F8.4} ~~ \text{Computation of}~ \mathrm{d}f_{8}\!\)

\(\begin{array}{c*{8}{l}} \mathrm{D}f_{8} & = & uv \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \\[6pt] \Downarrow \\[6pt] \mathrm{d}f_{8} & = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \end{array}\)


Computation of rf8


\(\text{Table F8.5} ~~ \text{Computation of}~ \mathrm{r}f_{8}\!\)

\(\begin{array}{c*{8}{l}} \mathrm{r}f_{8} & = & \mathrm{D}f_{8} ~+~ \mathrm{d}f_{8} \\[20pt] \mathrm{D}f_{8} & = & uv \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \\[6pt] \mathrm{d}f_{8} & = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \\[20pt] \mathrm{r}f_{8} & = & uv \cdot \mathrm{d}u ~ \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \end{array}\)


Computation Summary for Conjunction


\(\text{Table F8.6} ~~ \text{Computation Summary for}~ f_{8}(u, v) = uv\!\)

\(\begin{array}{c*{8}{l}} \boldsymbol\varepsilon f_{8} & = & uv \cdot 1 & + & u \texttt{(} v \texttt{)} \cdot 0 & + & \texttt{(} u \texttt{)} v \cdot 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \\[6pt] \mathrm{E}f_{8} & = & uv \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \\[6pt] \mathrm{D}f_{8} & = & uv \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \\[6pt] \mathrm{d}f_{8} & = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \\[6pt] \mathrm{r}f_{8} & = & uv \cdot \mathrm{d}u ~ \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \end{array}\)


Operator Maps for the Logical Equality f9(u, v)

Computation of εf9


\(\text{Table F9.1} ~~ \text{Computation of}~ \boldsymbol\varepsilon f_{9}\!\)

\(\begin{array}{*{10}{l}} \boldsymbol\varepsilon f_{9} & = && f_{9}(u, v) \\[4pt] & = && \texttt{((} u \texttt{,~} v \texttt{))} \\[4pt] & = && \texttt{ } u \texttt{ } v \texttt{ } \cdot f_{9}(1, 1) & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot f_{9}(1, 0) & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot f_{9}(0, 1) & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot f_{9}(0, 0) \\[4pt] & = && u v & + & 0 & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \\[20pt] \boldsymbol\varepsilon f_{9} & = && \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & 0 & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & 0 & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & 0 & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} & + & 0 & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} \end{array}\)


Computation of Ef9


\(\text{Table F9.2} ~~ \text{Computation of}~ \mathrm{E}f_{9}\!\)

\(\begin{array}{*{10}{l}} \mathrm{E}f_{9} & = && f_{9}(u + \mathrm{d}u, v + \mathrm{d}v) \\[4pt] & = && \texttt{(((} u \texttt{,} \mathrm{d}u \texttt{),(} v \texttt{,} \mathrm{d}v \texttt{)))} \\[4pt] & = && \texttt{ } u \texttt{ } v \texttt{ } \!\cdot\! f_{9}(\texttt{(} \mathrm{d}u \texttt{)}, \texttt{(} \mathrm{d}v \texttt{)}) & + & \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! f_{9}(\texttt{(} \mathrm{d}u \texttt{)}, \texttt{ } \mathrm{d}v \texttt{ }) & + & \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! f_{9}(\texttt{ } \mathrm{d}u \texttt{ }, \texttt{(} \mathrm{d}v \texttt{)}) & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! f_{9}(\texttt{ } \mathrm{d}u \texttt{ }, \texttt{ } \mathrm{d}v \texttt{ }) \\[4pt] & = && \texttt{ } u \texttt{ } v \texttt{ } \!\cdot\! \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))} & + & \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! \texttt{ (} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{) } & + & \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{ (} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{) } & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))} \\[20pt] \mathrm{E}f_{9} & = && \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & 0 & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} \\[4pt] && + & 0 & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & 0 \\[4pt] && + & 0 & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & 0 \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} & + & 0 & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} \end{array}\)


Computation of Df9


\(\text{Table F9.3-i} ~~ \text{Computation of}~ \mathrm{D}f_{9} ~\text{(Method 1)}\!\)

\(\begin{array}{*{10}{l}} \mathrm{D}f_{9} & = && \mathrm{E}f_{9} & + & \boldsymbol\varepsilon f_{9} \\[4pt] & = && f_{9}(u + \mathrm{d}u, v + \mathrm{d}v) & + & f_{9}(u, v) \\[4pt] & = && \texttt{(((} u \texttt{,} \mathrm{d}u \texttt{),(} v \texttt{,} \mathrm{d}v \texttt{)))} & + & \texttt{((} u \texttt{,} v \texttt{))} \\[20pt] \mathrm{D}f_{9} & = && 0 & + & 0 & + & 0 & + & 0 \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} \\[4pt] && + & 0 & + & 0 & + & 0 & + & 0 \\[20pt] \mathrm{D}f_{9} & = && \texttt{ } u \texttt{ } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \end{array}\!\)


\(\text{Table F9.3-ii} ~~ \text{Computation of}~ \mathrm{D}f_{9} ~\text{(Method 2)}\!\)

\(\begin{array}{*{9}{l}} \mathrm{D}f_{9} & = & 0 \cdot \mathrm{d}u ~ \mathrm{d}v & + & 1 \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)} & + & 1 \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v & + & 0 \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} \end{array}\)


Computation of df9


\(\text{Table F9.4} ~~ \text{Computation of}~ \mathrm{d}f_{9}\!\)

\(\begin{array}{c*{8}{l}} \mathrm{D}f_{9} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] \Downarrow \\[6pt] \mathrm{d}f_{9} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \end{array}\)


Computation of rf9


\(\text{Table F9.5} ~~ \text{Computation of}~ \mathrm{r}f_{9}\!\)

\(\begin{array}{c*{8}{l}} \mathrm{r}f_{9} & = & \mathrm{D}f_{9} ~+~ \mathrm{d}f_{9} \\[20pt] \mathrm{D}f_{9} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{d}f_{9} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[20pt] \mathrm{r}f_{9} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot 0 & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot 0 & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \end{array}\)


Computation Summary for Equality


\(\text{Table F9.6} ~~ \text{Computation Summary for}~ f_{9}(u, v) = \texttt{((} u \texttt{,} v \texttt{))}\!\)

\(\begin{array}{c*{8}{l}} \boldsymbol\varepsilon f_{9} & = & uv \cdot 1 & + & u \texttt{(} v \texttt{)} \cdot 0 & + & \texttt{(} u \texttt{)} v \cdot 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 1 \\[6pt] \mathrm{E}f_{9} & = & uv \cdot \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))} \\[6pt] \mathrm{D}f_{9} & = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{d}f_{9} & = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{r}f_{9} & = & uv \cdot 0 & + & u \texttt{(} v \texttt{)} \cdot 0 & + & \texttt{(} u \texttt{)} v \cdot 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \end{array}\)


Operator Maps for the Logical Implication f11(u, v)

Computation of εf11


\(\text{Table F11.1} ~~ \text{Computation of}~ \boldsymbol\varepsilon f_{11}\!\)

\(\begin{array}{*{10}{l}} \boldsymbol\varepsilon f_{11} & = && f_{11}(u, v) \\[4pt] & = && \texttt{(} u \texttt{(} v \texttt{))} \\[4pt] & = && \texttt{ } u \texttt{ } v \texttt{ } \cdot f_{11}(1, 1) & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot f_{11}(1, 0) & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot f_{11}(0, 1) & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot f_{11}(0, 0) \\[4pt] & = && \texttt{ } u \texttt{ } v \texttt{ } & + & 0 & + & \texttt{(} u \texttt{) } v \texttt{ } & + & \texttt{(} u \texttt{)(} v \texttt{)} \\[20pt] \boldsymbol\varepsilon f_{11} & = && \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & 0 & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & 0 & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & 0 & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} & + & 0 & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} \end{array}\!\)


Computation of Ef11


\(\text{Table F11.2} ~~ \text{Computation of}~ \mathrm{E}f_{11}\!\)

\(\begin{array}{*{10}{l}} \mathrm{E}f_{11} & = && f_{11}(u + \mathrm{d}u, v + \mathrm{d}v) \\[4pt] & = && \texttt{(} \\ &&& \qquad \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)} \\ &&& \texttt{(} \\ &&& \qquad \texttt{(} v \texttt{,} \mathrm{d}v \texttt{)} \\ &&& \texttt{))} \\[4pt] & = && u v \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)((} \mathrm{d}v \texttt{)))} & + & u \texttt{(} v \texttt{)} \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \!\cdot\! \texttt{(} \mathrm{d}u \texttt{((} \mathrm{d}v \texttt{)))} & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} \\[4pt] & = && u v \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \!\cdot\! \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} \\[20pt] \mathrm{E}f_{11} & = && \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & 0 & + & \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} \\[4pt] && + & 0 & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & 0 \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} \end{array}\)


Computation of Df11


\(\text{Table F11.3-i} ~~ \text{Computation of}~ \mathrm{D}f_{11} ~\text{(Method 1)}\!\)

\(\begin{array}{*{10}{l}} \mathrm{D}f_{11} & = && \mathrm{E}f_{11} & + & \boldsymbol\varepsilon f_{11} \\[4pt] & = && f_{11}(u + \mathrm{d}u, v + \mathrm{d}v) & + & f_{11}(u, v) \\[4pt] & = && \texttt{(} \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)} \texttt{(} \texttt{(} v \texttt{,} \mathrm{d}v \texttt{)} \texttt{))} & + & \texttt{(} u \texttt{(} v \texttt{))} \\[20pt] \mathrm{D}f_{11} & = && 0 & + & 0 & + & 0 & + & 0 \\[4pt] && + & u v \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & u \texttt{(} v \texttt{)} \!\cdot\! \texttt{~(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~~} & + & 0 & + & 0 \\[4pt] && + & 0 & + & u \texttt{(} v \texttt{)} \!\cdot\! \texttt{~~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)~} & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} \\[4pt] && + & 0 & + & u \texttt{(} v \texttt{)} \!\cdot\! \texttt{~~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~~} & + & \texttt{(} u \texttt{)} v \!\cdot\! \mathrm{d}u ~ \mathrm{d}v & + & 0 \\[20pt] \mathrm{D}f_{11} & = && u v \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & u \texttt{(} v \texttt{)} \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \!\cdot\! \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} \end{array}\)


\(\text{Table F11.3-ii} ~~ \text{Computation of}~ \mathrm{D}f_{11} ~\text{(Method 2)}\!\)

\(\begin{array}{c*{9}{l}} \mathrm{D}f_{11} & = & \boldsymbol\varepsilon f_{11} ~+~ \mathrm{E}f_{11} \\[20pt] \boldsymbol\varepsilon f_{11} & = & u v \cdot 1 & + & u \texttt{(} v \texttt{)} \cdot 0 & + & \texttt{(} u \texttt{)} v \cdot 1 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 1 \\[6pt] \mathrm{E}f_{11} & = & u v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} \\[20pt] \mathrm{D}f_{11} & = & u v \cdot \texttt{~(} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{~} & + & u \texttt{(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \cdot \texttt{~} \mathrm{d}u ~ \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)~} \end{array}\)


Computation of df11


\(\text{Table F11.4} ~~ \text{Computation of}~ \mathrm{d}f_{11}\!\)

\(\begin{array}{c*{8}{l}} \mathrm{D}f_{11} & = & u v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} \\[6pt] \Downarrow \\[6pt] \mathrm{d}f_{11} & = & u v \cdot \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \end{array}\)


Computation of rf11


\(\text{Table F11.5} ~~ \text{Computation of}~ \mathrm{r}f_{11}\!\)

\(\begin{array}{c*{8}{l}} \mathrm{r}f_{11} & = & \mathrm{D}f_{11} ~+~ \mathrm{d}f_{11} \\[20pt] \mathrm{D}f_{11} & = & u v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{d}f_{11} & = & u v \cdot \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \\[20pt] \mathrm{r}f_{11} & = & u v \cdot \mathrm{d}u ~ \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \end{array}\)


Computation Summary for Implication


\(\text{Table F11.6} ~~ \text{Computation Summary for}~ f_{11}(u, v) = \texttt{(} u \texttt{(} v \texttt{))}\!\)

\(\begin{array}{c*{8}{l}} \boldsymbol\varepsilon f_{11} & = & u v \cdot 1 & + & u \texttt{(} v \texttt{)} \cdot 0 & + & \texttt{(} u \texttt{)} v \cdot 1 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 1 \\[6pt] \mathrm{E}f_{11} & = & u v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} \\[6pt] \mathrm{D}f_{11} & = & u v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{d}f_{11} & = & u v \cdot \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \\[6pt] \mathrm{r}f_{11} & = & uv \cdot \mathrm{d}u ~ \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \end{array}\)


Operator Maps for the Logical Disjunction f14(u, v)

Computation of εf14


\(\text{Table F14.1} ~~ \text{Computation of}~ \boldsymbol\varepsilon f_{14}\!\)

\(\begin{array}{*{10}{l}} \boldsymbol\varepsilon f_{14} & = && f_{14}(u, v) \\[4pt] & = && \texttt{((} u \texttt{)(} v \texttt{))} \\[4pt] & = && \texttt{ } u \texttt{ } v \texttt{ } \cdot f_{14}(1, 1) & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot f_{14}(1, 0) & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot f_{14}(0, 1) & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot f_{14}(0, 0) \\[4pt] & = && \texttt{ } u \texttt{ } v \texttt{ } & + & \texttt{ } u \texttt{ (} v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } & + & 0 \\[20pt] \boldsymbol\varepsilon f_{14} & = && \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & 0 \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & 0 \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & 0 \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} & + & 0 \end{array}\)


Computation of Ef14


\(\text{Table F14.2} ~~ \text{Computation of}~ \mathrm{E}f_{14}\!\)

\(\begin{array}{*{10}{l}} \mathrm{E}f_{14} & = && f_{14}(u + \mathrm{d}u, v + \mathrm{d}v) \\[4pt] & = && \texttt{((} \\ &&& \qquad \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)} \\ &&& \texttt{)(} \\ &&& \qquad \texttt{(} v \texttt{,} \mathrm{d}v \texttt{)} \\ &&& \texttt{))} \\[4pt] & = && \texttt{ } u \texttt{ } v \texttt{ } \!\cdot\! f_{14}(\texttt{(} \mathrm{d}u \texttt{)}, \texttt{(} \mathrm{d}v \texttt{)}) & + & \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! f_{14}(\texttt{(} \mathrm{d}u \texttt{)}, \texttt{ } \mathrm{d}v \texttt{ }) & + & \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! f_{14}(\texttt{ } \mathrm{d}u \texttt{ }, \texttt{(} \mathrm{d}v \texttt{)}) & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! f_{14}(\texttt{ } \mathrm{d}u \texttt{ }, \texttt{ } \mathrm{d}v \texttt{ }) \\[4pt] & = && \texttt{ } u \texttt{ } v \texttt{ } \!\cdot\! \texttt{(} \mathrm{d}u \texttt{~} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \!\cdot\! \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{) } v \texttt{ } \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \\[20pt] \mathrm{E}f_{14} & = && \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & 0 \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} \\[4pt] && + & \texttt{ } u \texttt{ } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & 0 & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} \\[4pt] && + & 0 & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~} \end{array}\)


Computation of Df14


\(\text{Table F14.3-i} ~~ \text{Computation of}~ \mathrm{D}f_{14} ~\text{(Method 1)}\!\)

\(\begin{array}{*{10}{l}} \mathrm{D}f_{14} & = && \mathrm{E}f_{14} & + & \boldsymbol\varepsilon f_{14} \\[4pt] & = && f_{14}(u + \mathrm{d}u, v + \mathrm{d}v) & + & f_{14}(u, v) \\[4pt] & = && \texttt{(((} u \texttt{,} \mathrm{d}u \texttt{))((} v \texttt{,} \mathrm{d}v \texttt{)))} & + & \texttt{((} u \texttt{)(} v \texttt{))} \\[20pt] \mathrm{D}f_{14} & = && 0 & + & 0 & + & 0 & + & 0 \\[4pt] && + & 0 & + & 0 & + & \texttt{(} u \texttt{)} v \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{~(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~~} \\[4pt] && + & 0 & + & u \texttt{(} v \texttt{)} \!\cdot\! \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{~~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)~} \\[4pt] && + & uv \!\cdot\! \mathrm{d}u ~ \mathrm{d}v & + & 0 & + & 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{~~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~~} \\[20pt] \mathrm{D}f_{14} & = && uv \!\cdot\! \mathrm{d}u ~ \mathrm{d}v & + & u \texttt{(} v \texttt{)} \!\cdot\! \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \!\cdot\! \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \!\cdot\! \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \end{array}\)


\(\text{Table F14.3-ii} ~~ \text{Computation of}~ \mathrm{D}f_{14} ~\text{(Method 2)}\!\)

\(\begin{array}{*{9}{l}} \mathrm{D}f_{14} & = & \texttt{((} u \texttt{,} v \texttt{))} \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & 0 \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} \end{array}\)


Computation of df14


\(\text{Table F14.4} ~~ \text{Computation of}~ \mathrm{d}f_{14}\!\)

\(\begin{array}{c*{8}{l}} \mathrm{D}f_{14} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \\[6pt] \Downarrow \\[6pt] \mathrm{d}f_{14} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot 0 & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \mathrm{d}u & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \end{array}\)


Computation of rf14


\(\text{Table F14.5} ~~ \text{Computation of}~ \mathrm{r}f_{14}\!\)

\(\begin{array}{c*{8}{l}} \mathrm{r}f_{14} & = & \mathrm{D}f_{14} ~+~ \mathrm{d}f_{14} \\[20pt] \mathrm{D}f_{14} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \mathrm{d}u ~ \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)} ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \\[6pt] \mathrm{d}f_{14} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot 0 & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \mathrm{d}u & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[20pt] \mathrm{r}f_{14} & = & \texttt{ } u \texttt{ } v \texttt{ } \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{ } u \texttt{ (} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{) } v \texttt{ } \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \end{array}\)


Computation Summary for Disjunction


\(\text{Table F14.6} ~~ \text{Computation Summary for}~ f_{14}(u, v) = \texttt{((} u \texttt{)(} v \texttt{))}\!\)

\(\begin{array}{c*{8}{l}} \boldsymbol\varepsilon f_{14} & = & uv \cdot 1 & + & u \texttt{(} v \texttt{)} \cdot 1 & + & \texttt{(} u \texttt{)} v \cdot 1 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \\[6pt] \mathrm{E}f_{14} & = & uv \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \\[6pt] \mathrm{D}f_{14} & = & uv \cdot \mathrm{d}u ~ \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \\[6pt] \mathrm{d}f_{14} & = & uv \cdot 0 & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{r}f_{14} & = & uv \cdot \mathrm{d}u ~ \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v \end{array}\)


Appendix 4. Source Materials

Appendix 5. Various Definitions of the Tangent Vector

References

  • Ashby, William Ross (1956/1964), An Introduction to Cybernetics, Chapman and Hall, London, UK, 1956. Reprinted, Methuen and Company, London, UK, 1964.
  • Awbrey, J., and Awbrey, S. (1989), "Theme One : A Program of Inquiry", Unpublished Manuscript, 09 Aug 1989. Microsoft Word Document.
  • Edelman, Gerald M. (1988), Topobiology : An Introduction to Molecular Embryology, Basic Books, New York, NY.
  • Leibniz, Gottfried Wilhelm, Freiherr von, Theodicy : Essays on the Goodness of God, The Freedom of Man, and The Origin of Evil, Austin Farrer (ed.), E.M. Huggard (trans.), based on C.J. Gerhardt (ed.), Collected Philosophical Works, 1875–1890, Routledge and Kegan Paul, London, UK, 1951. Reprinted, Open Court, La Salle, IL, 1985.
  • McClelland, James L., and Rumelhart, David E. (1988), Explorations in Parallel Distributed Processing : A Handbook of Models, Programs, and Exercises, MIT Press, Cambridge, MA.
Retrieved from "https://mywikibiz.com/index.php?title=Directory:Jon_Awbrey/Papers/Differential_Propositional_Calculus&oldid=467575"