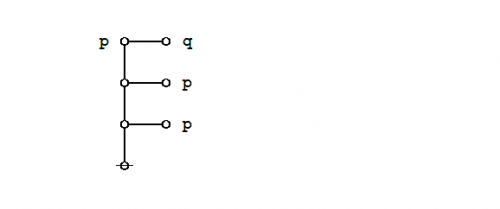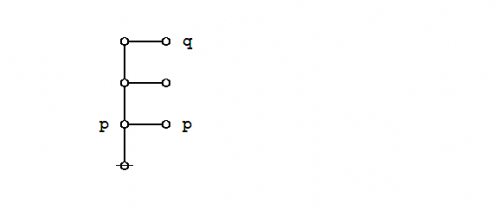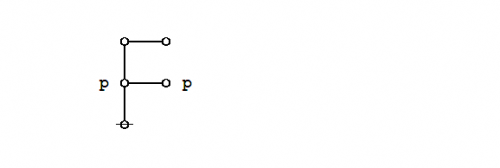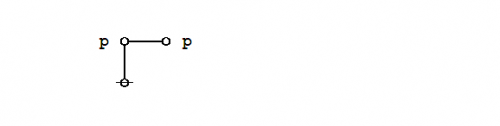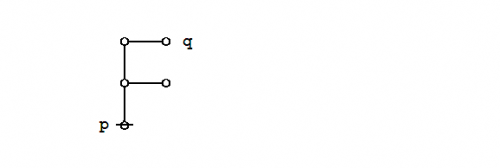Difference between revisions of "Peirce's law"

MyWikiBiz, Author Your Legacy — Tuesday November 26, 2024
Jump to navigationJump to search
(tweak format)
 
(38 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
'''Peirce's law''' is a proposition in [[propositional calculus]] that is commonly expressed in the following form:
+
<font size="3">&#9758;</font> This page belongs to resource collections on [[Logic Live|Logic]] and [[Inquiry Live|Inquiry]].
  
−
<center>
+
'''Peirce's law''' is a formula in [[propositional calculus]] that is commonly expressed in the following form:
−
<p><math>((p \Rightarrow q) \Rightarrow p) \Rightarrow p</math></p>
+
 
−
</center>
+
{| align="center" cellpadding="10"
 +
| <math>((p \Rightarrow q) \Rightarrow p) \Rightarrow p</math>
 +
|}
  
 
Peirce's law holds in classical propositional calculus, but not in intuitionistic propositional calculus.  The precise axiom system that one chooses for classical propositional calculus determines whether Peirce's law is taken as an axiom or proven as a theorem.
 
Peirce's law holds in classical propositional calculus, but not in intuitionistic propositional calculus.  The precise axiom system that one chooses for classical propositional calculus determines whether Peirce's law is taken as an axiom or proven as a theorem.
Line 11: Line 13:
 
Here is Peirce's own statement and proof of the law:
 
Here is Peirce's own statement and proof of the law:
  
−
<blockquote>
+
{| align="center" cellpadding="8" width="90%"
 +
|
 
<p>A ''fifth icon'' is required for the principle of excluded middle and other propositions connected with it.  One of the simplest formulae of this kind is:</p>
 
<p>A ''fifth icon'' is required for the principle of excluded middle and other propositions connected with it.  One of the simplest formulae of this kind is:</p>
  
 
<center>
 
<center>
−
<p><math>\{ (x \prec y) \prec x \} \prec x.</math></p>
+
<p><math>\{ (x \,-\!\!\!< y) \,-\!\!\!< x \} \,-\!\!\!< x.</math></p>
 
</center>
 
</center>
  
−
<p>This is hardly axiomatical.  That it is true appears as follows.  It can only be false by the final consequent <math>x\!</math> being false while its antecedent <math>(x \prec y) \prec x</math> is true.  If this is true, either its consequent, <math>x,\!</math> is true, when the whole formula would be true, or its antecedent <math>x \prec y</math> is false.  But in the last case the antecedent of <math>x \prec y,</math> that is <math>x,\!</math> must be true.  (Peirce, CP&nbsp;3.384).</p>
+
<p>This is hardly axiomatical.  That it is true appears as follows.  It can only be false by the final consequent <math>x\!</math> being false while its antecedent <math>(x \,-\!\!\!< y) \,-\!\!\!< x</math> is true.  If this is true, either its consequent, <math>x,\!</math> is true, when the whole formula would be true, or its antecedent <math>x \,-\!\!\!< y</math> is false.  But in the last case the antecedent of <math>x \,-\!\!\!< y,</math> that is <math>x,\!</math> must be true.  (Peirce, CP&nbsp;3.384).</p>
−
</blockquote>
+
|}
  
 
Peirce goes on to point out an immediate application of the law:
 
Peirce goes on to point out an immediate application of the law:
  
−
<blockquote>
+
{| align="center" cellpadding="8" width="90%"
 +
|
 
<p>From the formula just given, we at once get:</p>
 
<p>From the formula just given, we at once get:</p>
  
 
<center>
 
<center>
−
<p><math>\{ (x \prec y) \prec a \} \prec x,</math></p>
+
<p><math>\{ (x \,-\!\!\!< y) \,-\!\!\!< a \} \,-\!\!\!< x,</math></p>
 
</center>
 
</center>
  
−
<p>where the <math>a\!</math> is used in such a sense that <math>(x \prec y) \prec a</math> means that from <math>(x \prec y)</math> every proposition follows.  With that understanding, the formula states the principle of excluded middle, that from the falsity of the denial of <math>x\!</math> follows the truth of <math>x.\!</math>  (Peirce, CP&nbsp;3.384).</p>
+
<p>where the <math>a\!</math> is used in such a sense that <math>(x \,-\!\!\!< y) \,-\!\!\!< a</math> means that from <math>(x \,-\!\!\!< y)</math> every proposition follows.  With that understanding, the formula states the principle of excluded middle, that from the falsity of the denial of <math>x\!</math> follows the truth of <math>x.\!</math>  (Peirce, CP&nbsp;3.384).</p>
−
</blockquote>
+
|}
  
−
'''Note.'''  The above transcription uses the "precedes sign" (<math>\prec</math>) for the "sign of illation" that Peirce customarily wrote as a cursive symbol somewhat like a gamma (<math>\gamma\!</math>) turned on its side or else typed as a bigram consisting of a dash and a "less than" sign.
+
'''Note.'''  Peirce uses the ''sign of illation'' “<math>-\!\!\!<</math>” for implication.  In one place he explains “<math>-\!\!\!<</math>” as a variant of the sign “<math>\le</math>” for ''less than or equal to'';  in another place he suggests that <math>A \,-\!\!\!< B</math> is an iconic way of representing a state of affairs where <math>A,\!</math> in every way that it can be, is <math>B.\!</math>
  
−
==Graphic proof==
+
==Graphical proof==
  
−
Under the existential interpretation of Peirce's [[logical graph]]s, Peirce's law is represented by means of the following formal equivalence or logical equation.
+
Under the existential interpretation of Peirce's [[logical graphs]], Peirce's law is represented by means of the following formal equivalence or logical equation.
  
 
{| align="center" border="0" cellpadding="10" cellspacing="0"
 
{| align="center" border="0" cellpadding="10" cellspacing="0"
−
| [[Image:Peirce's_Law_Figure_1.jpg|500px]] || (1)
+
| [[Image:Peirce's Law 1.0 Splash Page.png|500px]] || (1)
 
|}
 
|}
  
 
'''Proof.'''  Using the axiom set given in the entry for [[logical graphs]], Peirce's law may be proved in the following manner.
 
'''Proof.'''  Using the axiom set given in the entry for [[logical graphs]], Peirce's law may be proved in the following manner.
 +
 +
{| align="center" cellpadding="8"
 +
|
 +
{| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center"
 +
|-
 +
| [[Image:Peirce's Law 1.0 Marquee Title.png|500px]]
 +
|-
 +
| [[Image:Peirce's Law 1.0 Storyboard 1.png|500px]]
 +
|-
 +
| [[Image:Equational Inference Band Collect p.png|500px]]
 +
|-
 +
| [[Image:Peirce's Law 1.0 Storyboard 2.png|500px]]
 +
|-
 +
| [[Image:Equational Inference Band Quit ((q)).png|500px]]
 +
|-
 +
| [[Image:Peirce's Law 1.0 Storyboard 3.png|500px]]
 +
|-
 +
| [[Image:Equational Inference Band Cancel (( )).png|500px]]
 +
|-
 +
| [[Image:Peirce's Law 1.0 Storyboard 4.png|500px]]
 +
|-
 +
| [[Image:Equational Inference Band Delete p.png|500px]]
 +
|-
 +
| [[Image:Peirce's Law 1.0 Storyboard 5.png|500px]]
 +
|-
 +
| [[Image:Equational Inference Band Cancel (( )).png|500px]]
 +
|-
 +
| [[Image:Peirce's Law 1.0 Storyboard 6.png|500px]]
 +
|-
 +
| [[Image:Equational Inference Marquee QED.png|500px]]
 +
|}
 +
| (2)
 +
|}
 +
 +
The following animation replays the steps of the proof.
 +
 +
{| align="center" cellpadding="8"
 +
|
 +
{| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center"
 +
|-
 +
| [[Image:Peirce's Law 2.0 Animation.gif]]
 +
|}
 +
| (3)
 +
|}
 +
 +
==Equational form==
 +
 +
A stronger form of Peirce's law also holds, in which the final implication is observed to be reversible:
 +
 +
{| align="center" cellpadding="10"
 +
| <math>((p \Rightarrow q) \Rightarrow p) \Leftrightarrow p</math>
 +
|}
 +
 +
===Proof 1===
 +
 +
Given what precedes, it remains to show that:
 +
 +
{| align="center" cellpadding="10"
 +
| <math>p \Rightarrow ((p \Rightarrow q) \Rightarrow p)</math>
 +
|}
 +
 +
But this is immediate, since <math>p \Rightarrow (r \Rightarrow p)</math> for any proposition <math>r.\!</math>
 +
 +
===Proof 2===
 +
 +
Representing propositions as logical graphs under the existential interpretation, the strong form of Peirce's law is expressed by the following equation:
  
 
{| align="center" border="0" cellpadding="10" cellspacing="0"
 
{| align="center" border="0" cellpadding="10" cellspacing="0"
−
| [[Image:Peirce's_Law_Figure_2.jpg|500px]] || (2)
+
| [[Image:Peirce's Law Strong Form 1.0 Splash Page.png|500px]] || (4)
 +
|}
 +
 
 +
Using the axioms and theorems listed in the article on [[logical graphs]], the equational form of Peirce's law may be proved in the following manner:
 +
 
 +
{| align="center" cellpadding="8"
 +
|
 +
{| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center"
 +
|-
 +
| [[Image:Peirce's Law Strong Form 1.0 Marquee Title.png|500px]]
 +
|-
 +
| [[Image:Peirce's Law Strong Form 1.0 Storyboard 1.png|500px]]
 +
|-
 +
| [[Image:Equational Inference Rule Collect p.png|500px]]
 +
|-
 +
| [[Image:Peirce's Law Strong Form 1.0 Storyboard 2.png|500px]]
 +
|-
 +
| [[Image:Equational Inference Rule Quit ((q)).png|500px]]
 +
|-
 +
| [[Image:Peirce's Law Strong Form 1.0 Storyboard 3.png|500px]]
 +
|-
 +
| [[Image:Equational Inference Rule Cancel (( )).png|500px]]
 +
|-
 +
| [[Image:Peirce's Law Strong Form 1.0 Storyboard 4.png|500px]]
 +
|-
 +
| [[Image:Equational Inference Marquee QED.png|500px]]
 +
|}
 +
| (5)
 +
|}
 +
 
 +
The following animation replays the steps of the proof.
 +
 
 +
{| align="center" cellpadding="8"
 +
|
 +
{| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center"
 +
|-
 +
| [[Image:Peirce's Law Strong Form 2.0 Animation.gif]]
 +
|}
 +
| (6)
 
|}
 
|}
  
Line 57: Line 165:
 
* Peirce, Charles Sanders (1981&ndash;), ''Writings of Charles S. Peirce : A Chronological Edition'', Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN.  Cited as (CE&nbsp;volume,&nbsp;page).
 
* Peirce, Charles Sanders (1981&ndash;), ''Writings of Charles S. Peirce : A Chronological Edition'', Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN.  Cited as (CE&nbsp;volume,&nbsp;page).
  
−
==See also==
+
==Syllabus==
 +
 
 +
===Focal nodes===
 +
 
 +
* [[Inquiry Live]]
 +
* [[Logic Live]]
 +
 
 +
===Peer nodes===
 +
 
 +
* [http://intersci.ss.uci.edu/wiki/index.php/Peirce's_law Peirce's Law @ InterSciWiki]
 +
* [http://mywikibiz.com/Peirce's_law Peirce's Law @ MyWikiBiz]
 +
* [http://ref.subwiki.org/wiki/Peirce's_law Peirce's Law @ Subject Wikis]
 +
* [http://en.wikiversity.org/wiki/Peirce's_law Peirce's Law @ Wikiversity]
 +
* [http://beta.wikiversity.org/wiki/Peirce's_law Peirce's Law @ Wikiversity Beta]
 +
 
 +
===Logical operators===
 +
 
 +
{{col-begin}}
 +
{{col-break}}
 +
* [[Exclusive disjunction]]
 +
* [[Logical conjunction]]
 +
* [[Logical disjunction]]
 +
* [[Logical equality]]
 +
{{col-break}}
 +
* [[Logical implication]]
 +
* [[Logical NAND]]
 +
* [[Logical NNOR]]
 +
* [[Logical negation|Negation]]
 +
{{col-end}}
  
−
* [[Charles Sanders Peirce]]
+
===Related topics===
 +
 
 +
{{col-begin}}
 +
{{col-break}}
 +
* [[Ampheck]]
 +
* [[Boolean domain]]
 +
* [[Boolean function]]
 +
* [[Boolean-valued function]]
 +
* [[Differential logic]]
 +
{{col-break}}
 
* [[Logical graph]]
 
* [[Logical graph]]
 +
* [[Minimal negation operator]]
 +
* [[Multigrade operator]]
 +
* [[Parametric operator]]
 +
* [[Peirce's law]]
 +
{{col-break}}
 
* [[Propositional calculus]]
 
* [[Propositional calculus]]
 +
* [[Sole sufficient operator]]
 +
* [[Truth table]]
 +
* [[Universe of discourse]]
 
* [[Zeroth order logic]]
 
* [[Zeroth order logic]]
 +
{{col-end}}
 +
 +
===Relational concepts===
 +
 +
{{col-begin}}
 +
{{col-break}}
 +
* [[Continuous predicate]]
 +
* [[Hypostatic abstraction]]
 +
* [[Logic of relatives]]
 +
* [[Logical matrix]]
 +
{{col-break}}
 +
* [[Relation (mathematics)|Relation]]
 +
* [[Relation composition]]
 +
* [[Relation construction]]
 +
* [[Relation reduction]]
 +
{{col-break}}
 +
* [[Relation theory]]
 +
* [[Relative term]]
 +
* [[Sign relation]]
 +
* [[Triadic relation]]
 +
{{col-end}}
 +
 +
===Information, Inquiry===
 +
 +
{{col-begin}}
 +
{{col-break}}
 +
* [[Inquiry]]
 +
* [[Dynamics of inquiry]]
 +
{{col-break}}
 +
* [[Semeiotic]]
 +
* [[Logic of information]]
 +
{{col-break}}
 +
* [[Descriptive science]]
 +
* [[Normative science]]
 +
{{col-break}}
 +
* [[Pragmatic maxim]]
 +
* [[Truth theory]]
 +
{{col-end}}
 +
 +
===Related articles===
 +
 +
{{col-begin}}
 +
{{col-break}}
 +
* [http://intersci.ss.uci.edu/wiki/index.php/Cactus_Language Cactus Language]
 +
* [http://intersci.ss.uci.edu/wiki/index.php/Futures_Of_Logical_Graphs Futures Of Logical Graphs]
 +
* [http://intersci.ss.uci.edu/wiki/index.php/Propositional_Equation_Reasoning_Systems Propositional Equation Reasoning Systems]
 +
{{col-break}}
 +
* [http://intersci.ss.uci.edu/wiki/index.php/Differential_Logic_:_Introduction Differential Logic : Introduction]
 +
* [http://intersci.ss.uci.edu/wiki/index.php/Differential_Propositional_Calculus Differential Propositional Calculus]
 +
* [http://intersci.ss.uci.edu/wiki/index.php/Differential_Logic_and_Dynamic_Systems_2.0 Differential Logic and Dynamic Systems]
 +
{{col-break}}
 +
* [http://intersci.ss.uci.edu/wiki/index.php/Prospects_for_Inquiry_Driven_Systems Prospects for Inquiry Driven Systems]
 +
* [http://intersci.ss.uci.edu/wiki/index.php/Introduction_to_Inquiry_Driven_Systems Introduction to Inquiry Driven Systems]
 +
* [http://intersci.ss.uci.edu/wiki/index.php/Inquiry_Driven_Systems Inquiry Driven Systems : Inquiry Into Inquiry]
 +
{{col-end}}
 +
 +
==Document history==
 +
 +
Portions of the above article were adapted from the following sources under the [[GNU Free Documentation License]], under other applicable licenses, or by permission of the copyright holders.
 +
 +
* [http://intersci.ss.uci.edu/wiki/index.php/Peirce's_law Peirce's Law], [http://intersci.ss.uci.edu/ InterSciWiki]
 +
* [http://mywikibiz.com/Peirce's_law Peirce's Law], [http://mywikibiz.com/ MyWikiBiz]
 +
* [http://planetmath.org/PeircesLaw Peirce's Law], [http://planetmath.org/ PlanetMath]
 +
* [http://wikinfo.org/w/index.php/Peirce's_law Peirce's Law], [http://www.wikinfo.org/w/ Wikinfo]
 +
* [http://en.wikiversity.org/wiki/Peirce's_law Peirce's Law], [http://en.wikiversity.org/ Wikiversity]
 +
* [http://beta.wikiversity.org/wiki/Peirce's_law Peirce's Law], [http://beta.wikiversity.org/ Wikiversity Beta]
 +
* [http://en.wikipedia.org/w/index.php?title=Peirce's_law&oldid=60606482 Peirce's Law], [http://en.wikipedia.org/ Wikipedia]
 +
 +
[[Category:Artificial Intelligence]]
 +
[[Category:Charles Sanders Peirce]]
 +
[[Category:Combinatorics]]
 +
[[Category:Computer Science]]
 +
[[Category:Cybernetics]]
 +
[[Category:Equational Reasoning]]
 +
[[Category:Formal Languages]]
 +
[[Category:Formal Systems]]
 +
[[Category:Graph Theory]]
 +
[[Category:History of Logic]]
 +
[[Category:History of Mathematics]]
 +
[[Category:Inquiry]]
 +
[[Category:Knowledge Representation]]
 +
[[Category:Logic]]
 +
[[Category:Logical Graphs]]
 +
[[Category:Mathematics]]
 +
[[Category:Philosophy]]
 +
[[Category:Semiotics]]
 +
[[Category:Visualization]]

Latest revision as of 04:14, 18 November 2015

☞ This page belongs to resource collections on Logic and Inquiry.

Peirce's law is a formula in propositional calculus that is commonly expressed in the following form:

\(((p \Rightarrow q) \Rightarrow p) \Rightarrow p\)

Peirce's law holds in classical propositional calculus, but not in intuitionistic propositional calculus. The precise axiom system that one chooses for classical propositional calculus determines whether Peirce's law is taken as an axiom or proven as a theorem.

History

Here is Peirce's own statement and proof of the law:

A fifth icon is required for the principle of excluded middle and other propositions connected with it. One of the simplest formulae of this kind is:

\(\{ (x \,-\!\!\!< y) \,-\!\!\!< x \} \,-\!\!\!< x.\)

This is hardly axiomatical. That it is true appears as follows. It can only be false by the final consequent \(x\!\) being false while its antecedent \((x \,-\!\!\!< y) \,-\!\!\!< x\) is true. If this is true, either its consequent, \(x,\!\) is true, when the whole formula would be true, or its antecedent \(x \,-\!\!\!< y\) is false. But in the last case the antecedent of \(x \,-\!\!\!< y,\) that is \(x,\!\) must be true. (Peirce, CP 3.384).

Peirce goes on to point out an immediate application of the law:

From the formula just given, we at once get:

\(\{ (x \,-\!\!\!< y) \,-\!\!\!< a \} \,-\!\!\!< x,\)

where the \(a\!\) is used in such a sense that \((x \,-\!\!\!< y) \,-\!\!\!< a\) means that from \((x \,-\!\!\!< y)\) every proposition follows. With that understanding, the formula states the principle of excluded middle, that from the falsity of the denial of \(x\!\) follows the truth of \(x.\!\) (Peirce, CP 3.384).

Note. Peirce uses the sign of illation “\(-\!\!\!<\)” for implication. In one place he explains “\(-\!\!\!<\)” as a variant of the sign “\(\le\)” for less than or equal to; in another place he suggests that \(A \,-\!\!\!< B\) is an iconic way of representing a state of affairs where \(A,\!\) in every way that it can be, is \(B.\!\)

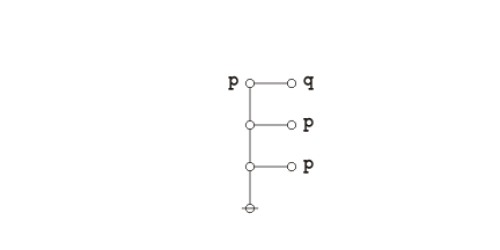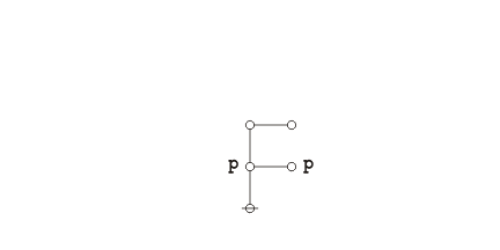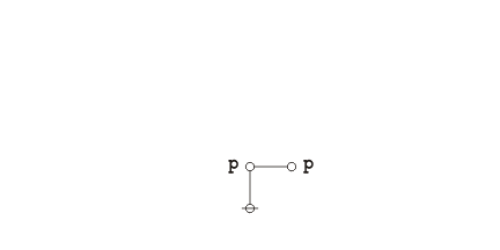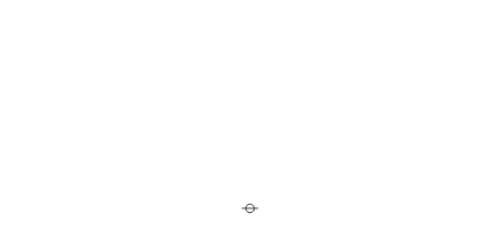
Graphical proof

Under the existential interpretation of Peirce's logical graphs, Peirce's law is represented by means of the following formal equivalence or logical equation.

Peirce's Law 1.0 Splash Page.png (1)

Proof. Using the axiom set given in the entry for logical graphs, Peirce's law may be proved in the following manner.

Peirce's Law 1.0 Marquee Title.png
Peirce's Law 1.0 Storyboard 1.png
Equational Inference Band Collect p.png
Peirce's Law 1.0 Storyboard 2.png
Equational Inference Band Quit ((q)).png
Peirce's Law 1.0 Storyboard 3.png
Equational Inference Band Cancel (( )).png
Peirce's Law 1.0 Storyboard 4.png
Equational Inference Band Delete p.png
Peirce's Law 1.0 Storyboard 5.png
Equational Inference Band Cancel (( )).png
Peirce's Law 1.0 Storyboard 6.png
Equational Inference Marquee QED.png
(2)

The following animation replays the steps of the proof.

Peirce's Law 2.0 Animation.gif
(3)

Equational form

A stronger form of Peirce's law also holds, in which the final implication is observed to be reversible:

\(((p \Rightarrow q) \Rightarrow p) \Leftrightarrow p\)

Proof 1

Given what precedes, it remains to show that:

\(p \Rightarrow ((p \Rightarrow q) \Rightarrow p)\)

But this is immediate, since \(p \Rightarrow (r \Rightarrow p)\) for any proposition \(r.\!\)

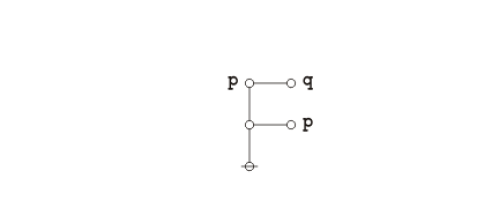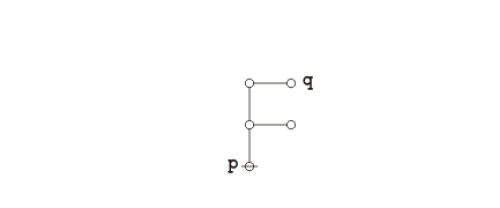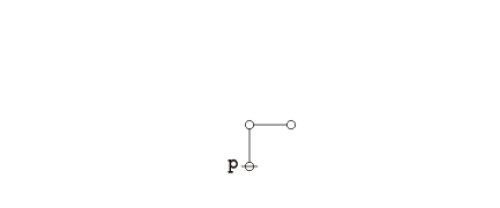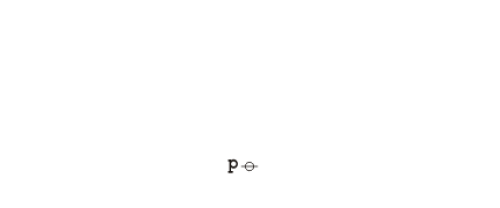
Proof 2

Representing propositions as logical graphs under the existential interpretation, the strong form of Peirce's law is expressed by the following equation:

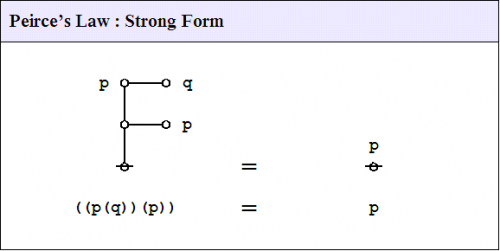Peirce's Law Strong Form 1.0 Splash Page.png (4)

Using the axioms and theorems listed in the article on logical graphs, the equational form of Peirce's law may be proved in the following manner:

Peirce's Law Strong Form 1.0 Marquee Title.png
Peirce's Law Strong Form 1.0 Storyboard 1.png
Equational Inference Rule Collect p.png
Peirce's Law Strong Form 1.0 Storyboard 2.png
Equational Inference Rule Quit ((q)).png
Peirce's Law Strong Form 1.0 Storyboard 3.png
Equational Inference Rule Cancel (( )).png
Peirce's Law Strong Form 1.0 Storyboard 4.png
Equational Inference Marquee QED.png
(5)

The following animation replays the steps of the proof.

Peirce's Law Strong Form 2.0 Animation.gif
(6)

Bibliography

  • Peirce, Charles Sanders (1885), "On the Algebra of Logic : A Contribution to the Philosophy of Notation", American Journal of Mathematics 7 (1885), 180–202. Reprinted (CP 3.359–403), (CE 5, 162–190).
  • Peirce, Charles Sanders (1931–1935, 1958), Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA. Cited as (CP volume.paragraph).
  • Peirce, Charles Sanders (1981–), Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN. Cited as (CE volume, page).

Syllabus

Focal nodes

Peer nodes

Logical operators

Template:Col-breakTemplate:Col-breakTemplate:Col-end

Related topics

Template:Col-breakTemplate:Col-breakTemplate:Col-breakTemplate:Col-end

Relational concepts

Template:Col-breakTemplate:Col-breakTemplate:Col-breakTemplate:Col-end

Information, Inquiry

Template:Col-breakTemplate:Col-breakTemplate:Col-breakTemplate:Col-breakTemplate:Col-end

Related articles

Template:Col-breakTemplate:Col-breakTemplate:Col-breakTemplate:Col-end

Document history

Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.

Retrieved from "https://mywikibiz.com/index.php?title=Peirce%27s_law&oldid=466922"