Difference between revisions of "Directory:Jon Awbrey/Papers/Differential Analytic Turing Automata"

MyWikiBiz, Author Your Legacy — Sunday November 17, 2024
Jump to navigationJump to search
(→‎Note 6: markup)
(update)
 
(181 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
{{DISPLAYTITLE:Differential Analytic Turing Automata}}
 
{{DISPLAYTITLE:Differential Analytic Turing Automata}}
 +
'''Author: [[User:Jon Awbrey|Jon Awbrey]]'''
  
−
==Note 1==
+
The task ahead is to chart a course from general ideas about ''transformational equivalence classes of graphs'' to a notion of ''differential analytic turing automata'' (DATA).  It may be a while before we get within sight of that goal, but it will provide a better measure of motivation to name the thread after the envisioned end rather than the more homely starting place.
  
−
For the purposes of the NKS Forum my aim is to chart a course from general ideas about ''transformational equivalence classes of graphs'' to a notion of ''differential analytic turing automata'' (DATA).  It may be a while before we get within sight of that goal, but it will provide some measure of motivation to name the thread after the envisioned end rather than the more homely starting place.
+
The basic idea is as follows.  One has a set <math>\mathcal{G}</math> of graphs and a set <math>\mathcal{T}</math> of transformation rules, and each rule <math>\mathrm{t} \in \mathcal{T}</math> has the effect of transforming graphs into graphs, <math>\mathrm{t} : \mathcal{G} \to \mathcal{G}.</math>  In the cases that we shall be studying, this set of transformation rules partitions the set of graphs into ''transformational equivalence classes'' (TECs).
−
 
 
−
The basic idea here is that you have a species of graphs and a set of transformation rules that take you from one graph to another &mdash; and back again, as I'm only thinking of equational rules &mdash; and this partitions the species of graphs into ''transformational equivalence classes'' (TECs).
 
  
 
There are many interesting excursions to be had here, but I will focus mainly on logical applications, and and so the TECs I talk about will almost always have the character of ''logical equivalence classes'' (LECs).
 
There are many interesting excursions to be had here, but I will focus mainly on logical applications, and and so the TECs I talk about will almost always have the character of ''logical equivalence classes'' (LECs).
  
−
An example that will figure heavily in the sequel is given by rooted trees as the species of graphs and a pair of equational transformation rules that derive from the graphical calculi of [[C.S. Peirce]], as revived and extended by George Spencer Brown.
+
An example that will figure heavily in the sequel is given by rooted trees as the species of graphs and a pair of equational transformation rules that derive from the graphical calculi of C.S. Peirce, as revived and extended by George Spencer Brown.
  
 
Here are the fundamental transformation rules, also referred to as the ''arithmetic axioms'', more precisely, the ''arithmetic initials''.
 
Here are the fundamental transformation rules, also referred to as the ''arithmetic axioms'', more precisely, the ''arithmetic initials''.
Line 21: Line 20:
 
That should be enough to get started.
 
That should be enough to get started.
  
−
==Note 2==
+
==Cactus Language==
  
 
I will be making use of the ''cactus language'' extension of Peirce's Alpha Graphs, so called because it uses a species of graphs that are usually called "cacti" in graph theory.  The last exposition of the cactus syntax that I've written can be found here:
 
I will be making use of the ''cactus language'' extension of Peirce's Alpha Graphs, so called because it uses a species of graphs that are usually called "cacti" in graph theory.  The last exposition of the cactus syntax that I've written can be found here:
  
−
:* [http://mywikibiz.com/Directory:Jon_Awbrey/Papers/Propositional_Equation_Reasoning_Systems Propositional Equation Reasoning Systems (PERS)]
+
:* [[Propositional Equation Reasoning Systems|Propositional Equation Reasoning Systems (PERS)]]
  
 
The representational and computational efficiency of the cactus language for the tasks that are usually associated with boolean algebra and propositional calculus makes it possible to entertain a further extension, to what we may call ''differential logic'', because it develops this basic level of logic in the same way that differential calculus augments analytic geometry to handle change and diversity.  There are several different introductions to differential logic that I have written and distributed across the Internet.  You might start with the following couple of treatments:
 
The representational and computational efficiency of the cactus language for the tasks that are usually associated with boolean algebra and propositional calculus makes it possible to entertain a further extension, to what we may call ''differential logic'', because it develops this basic level of logic in the same way that differential calculus augments analytic geometry to handle change and diversity.  There are several different introductions to differential logic that I have written and distributed across the Internet.  You might start with the following couple of treatments:
Line 32: Line 31:
 
:* [http://stderr.org/pipermail/inquiry/2004-February/thread.html#1160 Differential Logic B]
 
:* [http://stderr.org/pipermail/inquiry/2004-February/thread.html#1160 Differential Logic B]
  
−
I am currently rewriting these presentations in hopes of making them as clear as they can be, so please let me know if you have any questions.
+
I will draw on those previously advertised resources of notation and theory as needed, but right now I sense the need for some concrete examples.
−
 
 
−
==Note 3==
 
  
−
I will draw on those previously advertised resources of notation and theory as needed, but right now I sense the need for some concrete examples.
+
==Example 1==
  
−
Let's say we have a system that is known by the name of its state space <math>X\!</math> and we have a boolean state variable <math>x : X \to \mathbb{B},</math> where <math>\mathbb{B} = \{ 0, 1 \}.</math>
+
Let's say we have a system that is known by the name of its state space <math>X\!</math> and we have a boolean state variable <math>x : X \to \mathbb{B},\!</math> where <math>\mathbb{B} = \{ 0, 1 \}.\!</math>
  
 
We observe <math>X\!</math> for a while, relative to a discrete time frame, and we write down the following sequence of values for <math>x.\!</math>
 
We observe <math>X\!</math> for a while, relative to a discrete time frame, and we write down the following sequence of values for <math>x.\!</math>
Line 44: Line 41:
 
{| align="center" cellpadding="8" style="text-align:center"
 
{| align="center" cellpadding="8" style="text-align:center"
 
|
 
|
−
<math>\begin{array}{cc}
+
<math>\begin{array}{c|c}
−
t & x \\
+
t & x \\[8pt]
−
\\
 
 
0 & 0 \\
 
0 & 0 \\
 
1 & 1 \\
 
1 & 1 \\
Line 60: Line 56:
 
|}
 
|}
  
−
"Aha!" we say, and think we see the way of things, writing down the rule <math>x' = (x),\!</math> where <math>x'\!</math> is the state that comes next after <math>x,\!</math> and <math>(x)\!</math> is the negation of <math>x\!</math> in boolean logic.
+
&ldquo;Aha!&rdquo; we say, and think we see the way of things, writing down the rule <math>x' = \texttt{(} x \texttt{)},\!</math> where <math>x'\!</math> is the next state after <math>x\!</math> and <math>\texttt{(} x \texttt{)}\!</math> is the negation of <math>x\!</math> in boolean logic.
  
 
Another way to detect patterns is to write out a table of finite differences.  For this example, we would get:
 
Another way to detect patterns is to write out a table of finite differences.  For this example, we would get:
Line 66: Line 62:
 
{| align="center" cellpadding="8" style="text-align:center"
 
{| align="center" cellpadding="8" style="text-align:center"
 
|
 
|
−
<math>\begin{array}{ccccc}
+
<math>\begin{array}{c|cccc}
−
t &     x &     dx & d^2 x & \ldots \\
+
t & x & \mathrm{d}x & \mathrm{d}^2 x & \ldots \\[8pt]
−
\\
+
0 & 0 & 1 & 0 & \ldots \\
−
0 &     0 &     1 &     0 & \ldots \\
+
1 & 1 & 1 & 0 & \ldots \\
−
1 &     1 &     1 &     0 &       \\
+
2 & 0 & 1 & 0 & \ldots \\
−
2 &     0 &     1 &     0 &       \\
+
3 & 1 & 1 & 0 & \ldots \\
−
3 &     1 &     1 &     0 &       \\
+
4 & 0 & 1 & 0 & \ldots \\
−
4 &     0 &     1 &     0 &       \\
+
5 & 1 & 1 & 0 & \ldots \\
−
5 &     1 &     1 &     0 &       \\
+
6 & 0 & 1 & 0 & \ldots \\
−
6 &     0 &     1 &     0 &       \\
+
7 & 1 & 1 & 0 & \ldots \\
−
7 &     1 &     1 &     0 &       \\
+
8 & 0 & 1 & \ldots & \ldots \\
−
8 &     0 &     1 & \ldots &       \\
+
9 & \ldots & \ldots & \ldots & \ldots
−
9 & \ldots & \ldots & \ldots &       \\
 
 
\end{array}</math>
 
\end{array}</math>
 
|}
 
|}
Line 84: Line 79:
 
And of course, all the higher order differences are zero.
 
And of course, all the higher order differences are zero.
  
−
This leads to thinking of <math>X\!</math> as having an extended state <math>(x, dx, d^2 x, \ldots, d^k x),</math> and this additional language gives us the facility of describing state transitions in terms of the various orders of differences.  For example, the rule <math>x' = (x)\!</math> can now be expressed by the rule <math>dx = 1.\!</math>
+
This leads to thinking of <math>X\!</math> as having an extended state <math>(x, \mathrm{d}x, \mathrm{d}^2 x, \ldots, \mathrm{d}^k x),\!</math> and this additional language gives us the facility of describing state transitions in terms of the various orders of differences.  For example, the rule <math>x' = \texttt{(} x \texttt{)}\!</math> can now be expressed by the rule <math>{\mathrm{d}x = 1}.\!</math>
  
−
I'll leave you to muse on the possibilities of that.
+
There is a more detailed account of differential logic in the following paper:
  
−
==Note 4==
+
:* [[Differential Logic and Dynamic Systems 2.0|Differential Logic and Dynamic Systems]]
  
−
I am preparing a more fleshed-out 1-variable example, but in the mean time, for anybody who's finished all that other reading, there is a more detailed account of differential logic in the following paper:
+
For future reference, here are a couple of handy rosetta stones for translating back and forth between different notations for the boolean functions <math>f : \mathbb{B}^k \to \mathbb{B},\!</math> where <math>k = 1, 2.\!</math>
  
−
:* [[Directory:Jon_Awbrey/Papers/Differential_Logic_and_Dynamic_Systems_2.0|Differential Logic and Dynamic Systems]]
+
:* [[Differential Logic and Dynamic Systems 2.0#Tables of Propositional Forms|Tables of Propositional Forms]]
  
−
For future reference, here are a couple of handy rosetta stones for translating back and forth between different notations for the boolean functions <math>f : \mathbb{B}^k \to \mathbb{B},</math> where <math>k = 1, 2.\!</math>
+
==Example 2==
  
−
:* [[Directory:Jon_Awbrey/Papers/Differential_Logic_and_Dynamic_Systems_2.0#Tables_of_Propositional_Forms|Tables of Propositional Forms]]
+
For a slightly more interesting example, let's suppose that we have a dynamic system that is known by its state space <math>X\!</math> and we have a boolean state variable <math>x : X \to \mathbb{B}.\!</math>  In addition, we are given an initial condition <math>x = \mathrm{d}x\!</math> and a law <math>{\mathrm{d}^2 x = \texttt{(} x \texttt{)}}.\!</math>
  
−
==Note 5==
+
The initial condition has two cases:
  
−
For a slightly more interesting example, let's suppose that we have a dynamic system that is known by its state space <math>X,\!</math> and we have a boolean state variable <math>x : X \to \mathbb{B}.</math>  In addition, we are given an initial condition <math>x = dx\!</math> and a law <math>d^2 x = (x).\!</math>
+
{| align="center" cellpadding="8" width="90%"
−
 
+
|
−
The initial condition has two cases:  either &nbsp;<math>x = dx = 0\!</math>&nbsp; or &nbsp;<math>x = dx = 1.\!</math>
+
<math>\begin{array}{ll}
 +
1. & x ~=~ \mathrm{d}x ~=~ 0
 +
\\
 +
2. & x ~=~ \mathrm{d}x ~=~ 1
 +
\end{array}</math>
 +
|}
  
−
Here is a table of the two trajectories or ''orbits'' that we get by starting from each of the two permissible initial states and staying within the constraints of the dynamic law <math>d^2 x = (x).\!</math>
+
Here is a table of the two trajectories or ''orbits'' that we get by starting from each of the two permissible initial states and staying within the constraints of the dynamic law <math>{\mathrm{d}^2 x = \texttt{(} x \texttt{)}}.\!</math>
  
 
{| align="center" cellpadding="8" style="text-align:center"
 
{| align="center" cellpadding="8" style="text-align:center"
−
| <math>\text{Initial State}\ x \cdot dx</math>
+
| <math>\text{Initial State}~ x \cdot \mathrm{d}x\!</math>
 
|-
 
|-
 
|
 
|
−
<math>\begin{array}{cccc}
+
<math>\begin{array}{c|ccc}
−
t & d^0 x & d^1 x & d^2 x \\
+
t & \mathrm{d}^0 x & \mathrm{d}^1 x & \mathrm{d}^2 x \\[8pt]
−
\\
+
0 & 1 & 1 & 0 \\
−
0 &     1 &     1 &     0 \\
+
1 & 0 & 1 & 1 \\
−
1 &     0 &     1 &     1 \\
+
2 & 1 & 0 & 0 \\
−
2 &     1 &     0 &     0 \\
+
3 & 1 & 0 & 0 \\
−
3 &     1 &     0 &     0 \\
+
4 & 1 & 0 & 0 \\
−
4 &     1 &     0 &     0 \\
+
5 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel
−
5 &     '' &     '' &     '' \\
+
\end{array}</math>
−
\end{array}</math></p>
 
 
|}
 
|}
  
Line 125: Line 124:
  
 
{| align="center" cellpadding="8" style="text-align:center"
 
{| align="center" cellpadding="8" style="text-align:center"
−
| <math>\text{Initial State}\ (x) \cdot (dx)</math>
+
| <math>\text{Initial State}~ \texttt{(} x \texttt{)} \cdot \texttt{(} \mathrm{d}x \texttt{)}\!</math>
 
|-
 
|-
 
|
 
|
−
<math>\begin{array}{cccc}
+
<math>\begin{array}{c|ccc}
−
t & d^0 x & d^1 x & d^2 x \\
+
t & \mathrm{d}^0 x & \mathrm{d}^1 x & \mathrm{d}^2 x \\[8pt]
−
\\
+
0 & 0 & 0 & 1 \\
−
0 &     0 &     0 &     1 \\
+
1 & 0 & 1 & 1 \\
−
1 &     0 &     1 &     1 \\
+
2 & 1 & 0 & 0 \\
−
2 &     1 &     0 &     0 \\
+
3 & 1 & 0 & 0 \\
−
3 &     1 &     0 &     0 \\
+
4 & 1 & 0 & 0 \\
−
4 &     1 &     0 &     0 \\
+
5 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel
−
5 &     '' &     '' &     '' \\
 
 
\end{array}</math>
 
\end{array}</math>
 
|}
 
|}
  
−
Note that the state <math>x\ \underline{(} dx \underline{)}\ \underline{(} d^2 x \underline{)},</math> that is, <math>(x, dx, d^2 x) ~=~ (1, 0, 0),</math> is a stable attractor for both orbits.
+
Note that the state <math>x \texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}^2 x \texttt{)},\!</math> that is, <math>(x, \mathrm{d}x, \mathrm{d}^2 x) = (1, 0, 0),\!</math> is a stable attractor for both orbits.
  
 
Further discussion of this example, complete with charts and graphs, can be found at this location:
 
Further discussion of this example, complete with charts and graphs, can be found at this location:
  
−
:* [[Directory:Jon_Awbrey/Papers/Differential_Logic_and_Dynamic_Systems_2.0#Example_1._A_Square_Rigging|Example 1. A Square Rigging]]
+
:* [[Differential Logic and Dynamic Systems 2.0#Example 1. A Square Rigging|Example 1. A Square Rigging]]
  
−
==Note 6==
+
==Example 3==
  
−
One more example may serve to suggest just how much dynamic complexity can be built on a universe of discourse that has but a single logical feature at its base.
+
One more example may serve to suggest just how much dynamic complexity can be built on a universe of discourse that has but a single logical feature at its base.  But first, there are a few more elements of general notation that that we'll need to describe finite dimensional universes of discourse and the qualitative dynamics that we envision occurring in them.
  
−
But first, let me introduce a few more elements of general notation that I'll be using to describe finite dimensional universes of discourse and the qualitative dynamics that we envision occurring in them.
+
Let <math>\mathcal{X} = \{ x_1, \ldots, x_n \}\!</math> be the ''alphabet'' of logical ''features'' or ''variables'' that are used to describe the <math>n\!</math>-dimensional universe of discourse <math>X^\bullet = [\mathcal{X}]\!</math> <math>= [x_1, \ldots, x_n].\!</math>  One may picture a venn diagram whose <math>n\!</math> overlapping &ldquo;circles&rdquo; are labeled with the feature names in <math>\mathcal{X}.\!</math>  Staying with this picture, one visualizes the universe of discourse <math>X^\bullet = [\mathcal{X}]\!</math> as having two layers:
  
−
Let <math>\mathcal{X} = \{ x_1, \ldots, x_n \}</math> be the ''alphabet'' of logical ''features'' or ''variables'' that we use to describe the n-dimensional universe of discourse <math>X^\circ = [\mathcal{X}] = [ x_1, \ldots, x_n ].</math>  Picturesquely viewed, one may think of a venn diagram with n overlapping "circles" that are labeled with the feature names in the set <math>\mathcal{X}.</math>  Staying with this picture, one visualizes the universe of discourse <math>X^\circ = [\mathcal{X}]</math> as having two layers:  (1) the set <math>X = \langle \mathcal{X} \rangle = \langle x_1, \dots, x_n \rangle</math> of ''points'' or ''cells'' &mdash; in another sense of the word than when we speak of ''cellular automata'' &mdash; (2) the set <math>X^\uparrow = (X \to \mathbb{B})</math> of ''propositions'', boolean-valued functions, or maps from <math>X\!</math> to <math>\mathbb{B}.</math>
+
# The set <math>X = \langle \mathcal{X} \rangle = \langle x_1, \dots, x_n \rangle\!</math> of ''points'' or ''cells'' &mdash; the latter used in another sense of the word than when we speak of ''cellular automata''.
 +
# The set <math>X^\uparrow = (X \to \mathbb{B})\!</math> of ''propositions'', boolean-valued functions, or maps from <math>X\!</math> to <math>\mathbb{B}.\!</math>
  
−
Thus, we may speak of the universe of discourse <math>X^\circ</math> as being an ordered pair <math>(X, X^\uparrow),</math> with <math>2^n\!</math> points in the underlying space <math>X\!</math> and <math>2^{2^n}</math> propositions in the function space <math>X^\uparrow.</math>
+
Thus we picture the universe of discourse <math>{X^\bullet}\!</math> as an ordered pair <math>{X^\bullet = (X, X^\uparrow)}\!</math> having <math>2^n\!</math> points in the underlying space <math>X\!</math> and <math>2^{2^n}\!</math> propositions in the function space <math>X^\uparrow.\!</math>
  
 
A more complete discussion of these notations can be found here:
 
A more complete discussion of these notations can be found here:
  
−
:* [[Directory:Jon_Awbrey/Papers/Differential_Logic_and_Dynamic_Systems_2.0#A_Functional_Conception_of_Propositional_Calculus|A Functional Conception of Propositional Calculus]]
+
:* [[Differential Logic and Dynamic Systems 2.0#A Functional Conception of Propositional Calculus|A Functional Conception of Propositional Calculus]]
  
 
Now, to the Example.
 
Now, to the Example.
  
−
Once again, let us begin with a 1-feature alphabet <math>\mathcal{X} = \{ x_1 \} = \{ x \}.</math>  In the discussion that follows I will consider a class of trajectories that are ruled by the constraint that <math>d^k x = 0\!</math> for all <math>k\!</math> greater than some fixed <math>m,\!</math> and I will indulge in the use of some picturesque speech to describes salient classes of such curves.  Given this finite order condition, there is a highest order non-zero difference <math>d^m x\!</math> that is exhibited at each point in the course of any determinate trajectory.
+
Once again, let us begin with a 1-feature alphabet <math>\mathcal{X} = \{ x_1 \} = \{ x \}.\!</math>  In the discussion that follows I will consider a class of trajectories that are ruled by the constraint that <math>\mathrm{d}^k x = 0\!</math> for all <math>k\!</math> greater than some fixed <math>m\!</math> and I will indulge in the use of some picturesque language to describe salient classes of such curves.  Given the finite order condition, there is a highest order non-zero difference <math>\mathrm{d}^m x\!</math> that is exhibited at each point in the course of any determinate trajectory.  Relative to any point of the corresponding orbit or curve, let us call this highest order differential feature <math>\mathrm{d}^m x\!</math> the ''drive'' at that point.  Curves of constant drive <math>\mathrm{d}^m x\!</math> are then referred to as ''<math>m^\text{th}\!</math> gear curves''.
  
−
Relative to any point of the corresponding orbit or curve, let us call this highest order differential feature <math>d^m x\!</math> the ''drive'' at that point.  Curves of constant drive <math>d^m x\!</math> are then referred to as ''<math>m^\text{th}\!</math> gear curves''.
+
One additional piece of notation will be needed here.  Starting from the base alphabet <math>\mathcal{X} = \{ x \},\!</math> we define and notate <math>\mathrm{E}^j \mathcal{X} = \{ x, \mathrm{d}^1 x, \mathrm{d}^2 x, \ldots, \mathrm{d}^j x \}\!</math> as the ''<math>j^\text{th}\!</math> order extended alphabet over <math>\mathcal{X}.\!</math>''
  
−
<pre>
+
Let us now consider the family of 4<sup>th</sup> gear curves through the extended space <math>\mathrm{E}^4 X = \langle x, \mathrm{d}x, \mathrm{d}^2 x, \mathrm{d}^3 x, \mathrm{d}^4 x \rangle.\!</math>  These are the trajectories that are generated subject to the law <math>\mathrm{d}^4 x = 1,\!</math> where it is understood in making such a statement that all higher order differences are equal to <math>0.\!</math>
−
One additional piece of notation will be needed here.
 
−
Starting from the base alphabet !X! = {x}, we define
 
−
and notate E^j.!X! = {x, d^1.x, d^2.x, ..., d^j.x}
 
−
as the "j^th order extended alphabet over !X!".
 
  
−
Let us now consider the family of 4^th gear curves through
+
Since <math>\mathrm{d}^4 x\!</math> and all higher order <math>\mathrm{d}^j x\!</math> are fixed, the entire dynamics can be plotted in the extended space <math>\mathrm{E}^3 X = \langle x, \mathrm{d}x, \mathrm{d}^2 x, \mathrm{d}^3 x \rangle.\!</math> Thus, there is just enough room in a planar venn diagram to plot both orbits and to show how they partition the points of <math>\mathrm{E}^3 X.\!</math>  As it turns out, there are exactly two possible orbits, of eight points each, as illustrated in Figures&nbsp;16-a and 16-b. See here:
−
the extended space E^4.X = <|x, dx, d^2.x, d^3.x, d^4.x|>.
 
−
These are the trajectories that are generated subject to
 
−
the law d^4.x = 1, where it is understood in making such
 
−
a statement that all higher order differences equal 0.
 
  
−
Since d^4.x and all higher order d^j.x are fixed, the entire dynamics
+
:* [[Differential Logic and Dynamic Systems 2.0#Example 2. Drives and Their Vicissitudes|Example 2. Drives and Their Vicissitudes]]
−
can be plotted in the extended space E^3.X = <|x, dx, d^2.x, d^3.x|>.
 
−
Thus, there is just enough room in a planar venn diagram to plot all
 
−
of these orbits and to show how they partition the points of E^3.X.
 
−
As it turns out, there are exactly two possible orbits, of eight
 
−
points each, as illustrated in Figures 16-a and 16-b.  See here:
 
  
−
DLOG D23.  http://stderr.org/pipermail/inquiry/2003-May/000502.html
+
Here are the 4<sup>th</sup> gear curves over the 1-feature universe <math>X = \langle x \rangle\!</math> arranged in the form of tabular arrays, listing the extended state vectors <math>(x, \mathrm{d}x, \mathrm{d}^2 x, \mathrm{d}^3 x, \mathrm{d}^4 x)\!</math> as they occur in one cyclic period of each orbit.
  
−
Zoom^4 ...
+
{| align="center" cellpadding="8" style="text-align:center"
−
</pre>
+
| <math>\text{Orbit 1}\!</math>
 +
|-
 +
|
 +
<math>\begin{array}{c|ccccc}
 +
t & \mathrm{d}^0 x & \mathrm{d}^1 x & \mathrm{d}^2 x & \mathrm{d}^3 x & \mathrm{d}^4 x \\
 +
\\
 +
0 & 0 & 0 & 0 & 0 & 1 \\
 +
1 & 0 & 0 & 0 & 1 & 1 \\
 +
2 & 0 & 0 & 1 & 0 & 1 \\
 +
3 & 0 & 1 & 1 & 1 & 1 \\
 +
4 & 1 & 0 & 0 & 0 & 1 \\
 +
5 & 1 & 0 & 0 & 1 & 1 \\
 +
6 & 1 & 0 & 1 & 0 & 1 \\
 +
7 & 1 & 1 & 1 & 1 & 1
 +
\end{array}</math>
 +
|}
  
−
==Note 7==
+
<br>
  
−
<pre>
+
{| align="center" cellpadding="8" style="text-align:center"
−
Here are the 4^th gear curves over the 1-feature universe
+
| <math>\text{Orbit 2}\!</math>
−
X = <|x|> arranged in the form of tabular arrays, listing
+
|-
−
the extended state vectors <x, dx, d^2.x, d^3.x, d^4.x>
+
|
−
as they occur in one cyclic period of each orbit.
+
<math>\begin{array}{c|ccccc}
 +
t & \mathrm{d}^0 x & \mathrm{d}^1 x & \mathrm{d}^2 x & \mathrm{d}^3 x & \mathrm{d}^4 x \\
 +
\\
 +
0 & 1 & 1 & 0 & 0 & 1 \\
 +
1 & 0 & 1 & 0 & 1 & 1 \\
 +
2 & 1 & 1 & 1 & 0 & 1 \\
 +
3 & 0 & 0 & 1 & 1 & 1 \\
 +
4 & 0 & 1 & 0 & 0 & 1 \\
 +
5 & 1 & 1 & 0 & 1 & 1 \\
 +
6 & 0 & 1 & 1 & 0 & 1 \\
 +
7 & 1 & 0 & 1 & 1 & 1
 +
\end{array}</math>
 +
|}
  
−
d d d d d
+
In this arrangement, the temporal ordering of states can be reckoned by a kind of ''parallel round-up rule''. Specifically, if <math>(a_k, a_{k+1})\!</math> is any pair of adjacent digits in a state vector <math>{(a_0, a_1, \ldots, a_n)},\!</math> then the value of <math>a_k\!</math> in the next state is <math>a_k' = a_k + a_{k+1},\!</math> the addition being taken mod 2, of course.
−
0 1 2 3 4
 
−
x x x x x
 
−
 
 
−
Orbit 1
 
−
 
 
−
0 0 0 0 1
 
−
0 0 0 1 1
 
−
0 0 1 0 1
 
−
0 1 1 1 1
 
−
1 0 0 0 1
 
−
1 0 0 1 1
 
−
1 0 1 0 1
 
−
1 1 1 1 1
 
−
 
 
−
Orbit 2
 
−
 
 
−
1 1 0 0 1
 
−
0 1 0 1 1
 
−
1 1 1 0 1
 
−
0 0 1 1 1
 
−
0 1 0 0 1
 
−
1 1 0 1 1
 
−
0 1 1 0 1
 
−
1 0 1 1 1
 
−
 
 
−
In this arrangement, the temporal ordering of states
 
−
can be reckoned by a kind of "parallel round-up rule".
 
−
Specifically, if <a_k, a_[k+1]> is any pair of adjacent
 
−
digits in a state vector <a_0, a_1, ..., a_n>, then the
 
−
value of a_k in the next state is [a_k]' = a_k + a_[k+1],
 
−
the addition being taken mod 2, of course.
 
  
 
A more complete discussion of this arrangement is given here:
 
A more complete discussion of this arrangement is given here:
  
−
DLOG D24. http://stderr.org/pipermail/inquiry/2003-May/000503.html
+
:* [[Differential Logic and Dynamic Systems 2.0#Example 2. Drives and Their Vicissitudes|Example 2. Drives and Their Vicissitudes]]
−
</pre>
 
  
−
==Note 8==
+
==Example 4==
  
−
<pre>
+
I am going to tip-toe in silence/consilience past many questions of a philosophical nature/nurture that might be asked at this juncture, no doubt to revisit them at some future opportunity/importunity, however the cases happen to align in the course of their inevitable fall.
−
I am going to tip-toe in silence/consilience past many
 
−
questions of a philosophical nature/nurture that might
 
−
be asked at this juncture, no doubt to revisit them at
 
−
some future opportunity/importunity, however the cases
 
−
happen to align in the course of their inevitable fall.
 
  
−
Instead, let's "keep it concrete and simple", taking up the
+
Instead, let's follow the adage to &ldquo;keep it concrete and simple&rdquo;, taking up the consideration of an incrementally more complex example, but having a slightly more general character than the orders of sequential transformations that we've been discussing up to this point.
−
consideration of an incrementally more complex example, but
 
−
having a slightly more general character than the orders of
 
−
sequential transformations that we've been discussing up to
 
−
this point.
 
  
−
The types of logical transformations that I have in mind can
+
The types of logical transformations that I have in mind can be thought of as ''transformations of discourse'' because they map a universe of discourse into a universe of discourse by way of logical equations between the qualitative features or logical variables in the source and target universes.
−
be thought of as "transformations of discourse" because they
 
−
map a universe of discourse into a universe of discourse by
 
−
way of logical equations between the qualitative features
 
−
or logical variables in the source and target universes.
 
  
−
The sequential transformations or state transitions that we have
+
The sequential transformations or state transitions that we have been considering so far are actually special cases of these more general logical transformations, specifically, they are the ones that have a single universe of discourse, as it happens to exist at different moments in time, in the role of both the source and the target universes of the transformation in question.
−
been considering so far are actually special cases of these more
 
−
general logical transformations, specifically, they are the ones
 
−
that have a single universe of discourse, as it happens to exist
 
−
at different moments in time, in the role of both the source and
 
−
the target universes of the transformation in question.
 
  
−
Onward and upward to Flatland, the differential analysis of
+
Onward and upward to Flatland, the differential analysis of transformations between 2-dimensional universes of discourse.
−
transformations between 2-dimensional universes of discourse.
 
  
−
Consider the transformation from the universe U% = [u, v] to the
+
Consider the transformation from the universe <math>U^\bullet = [u, v]</math> to the universe <math>X^\bullet = [x, y]</math> that is defined by this system of equations:
−
universe X% = [x, y] that is defined by this system of equations:
 
  
−
x   =   f<u, v>  =   ((u)(v))
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{matrix}
 +
x & = & f(u, v) & = & \texttt{((} u \texttt{)(} v \texttt{))}
 +
\\[8pt]
 +
y & = & g(u, v) & = & \texttt{((} u \texttt{,~} v \texttt{))}
 +
\end{matrix}</math>
 +
|}
  
−
y  =  g<u, v>  =  ((u, v))
+
The parenthetical expressions on the right are the cactus forms for the boolean functions that correspond to inclusive disjunction and logical equivalence, respectively.  Table&nbsp;1 summarizes the basic elements of the cactus notation for propositional logic.
  
−
The parenthetical expressions on the right are the cactus forms for
+
<br>
−
the boolean functions that correspond to inclusive disjunction and
 
−
logical equivalence, respectively.  By way of a reminder, consult
 
−
Table 1 on the page at this location:
 
  
−
DLOG D1. http://stderr.org/pipermail/inquiry/2003-May/000478.html
+
{| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:75%"
 +
|+ style="height:30px" | <math>\text{Table 1.} ~~ \text{Syntax and Semantics of a Calculus for Propositional Logic}\!</math>
 +
|- style="height:40px; background:ghostwhite"
 +
| <math>\text{Graph}\!</math>
 +
| <math>\text{Expression}~\!</math>
 +
| <math>\text{Interpretation}\!</math>
 +
| <math>\text{Other Notations}\!</math>
 +
|-
 +
| height="100px" | [[Image:Cactus Node Big Fat.jpg|20px]]
 +
| <math>~</math>
 +
| <math>\operatorname{true}</math>
 +
| <math>1\!</math>
 +
|-
 +
| height="100px" | [[Image:Cactus Spike Big Fat.jpg|20px]]
 +
| <math>\texttt{(~)}</math>
 +
| <math>\operatorname{false}</math>
 +
| <math>0\!</math>
 +
|-
 +
| height="100px" | [[Image:Cactus A Big.jpg|20px]]
 +
| <math>a\!</math>
 +
| <math>a\!</math>
 +
| <math>a\!</math>
 +
|-
 +
| height="120px" | [[Image:Cactus (A) Big.jpg|20px]]
 +
| <math>\texttt{(} a \texttt{)}~</math>
 +
| <math>\operatorname{not}~ a</math>
 +
| <math>\lnot a \quad \bar{a} \quad \tilde{a} \quad a^\prime</math>
 +
|-
 +
| height="100px" | [[Image:Cactus ABC Big.jpg|50px]]
 +
| <math>a ~ b ~ c</math>
 +
| <math>a ~\operatorname{and}~ b ~\operatorname{and}~ c</math>
 +
| <math>a \land b \land c</math>
 +
|-
 +
| height="160px" | [[Image:Cactus ((A)(B)(C)) Big.jpg|65px]]
 +
| <math>\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}</math>
 +
| <math>a ~\operatorname{or}~ b ~\operatorname{or}~ c</math>
 +
| <math>a \lor b \lor c</math>
 +
|-
 +
| height="120px" | [[Image:Cactus (A(B)) Big.jpg|60px]]
 +
| <math>\texttt{(} a \texttt{(} b \texttt{))}</math>
 +
|
 +
<math>\begin{matrix}
 +
a ~\operatorname{implies}~ b
 +
\\[6pt]
 +
\operatorname{if}~ a ~\operatorname{then}~ b
 +
\end{matrix}</math>
 +
| <math>a \Rightarrow b</math>
 +
|-
 +
| height="120px" | [[Image:Cactus (A,B) Big ISW.jpg|65px]]
 +
| <math>\texttt{(} a \texttt{,} b \texttt{)}</math>
 +
|
 +
<math>\begin{matrix}
 +
a ~\operatorname{not~equal~to}~ b
 +
\\[6pt]
 +
a ~\operatorname{exclusive~or}~ b
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
a \neq b
 +
\\[6pt]
 +
a + b
 +
\end{matrix}</math>
 +
|-
 +
| height="160px" | [[Image:Cactus ((A,B)) Big.jpg|65px]]
 +
| <math>\texttt{((} a \texttt{,} b \texttt{))}</math>
 +
|
 +
<math>\begin{matrix}
 +
a ~\operatorname{is~equal~to}~ b
 +
\\[6pt]
 +
a ~\operatorname{if~and~only~if}~ b
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
a = b
 +
\\[6pt]
 +
a \Leftrightarrow b
 +
\end{matrix}</math>
 +
|-
 +
| height="120px" | [[Image:Cactus (A,B,C) Big.jpg|65px]]
 +
| <math>\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}</math>
 +
|
 +
<math>\begin{matrix}
 +
\operatorname{just~one~of}
 +
\\
 +
a, b, c
 +
\\
 +
\operatorname{is~false}.
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
& \bar{a} ~ b ~ c
 +
\\
 +
\lor & a ~ \bar{b} ~ c
 +
\\
 +
\lor & a ~ b ~ \bar{c}
 +
\end{matrix}</math>
 +
|-
 +
| height="160px" | [[Image:Cactus ((A),(B),(C)) Big.jpg|65px]]
 +
| <math>\texttt{((} a \texttt{),(} b \texttt{),(} c \texttt{))}</math>
 +
|
 +
<math>\begin{matrix}
 +
\operatorname{just~one~of}
 +
\\
 +
a, b, c
 +
\\
 +
\operatorname{is~true}.
 +
\\[6pt]
 +
\operatorname{partition~all}
 +
\\
 +
\operatorname{into}~ a, b, c.
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
& a ~ \bar{b} ~ \bar{c}
 +
\\
 +
\lor & \bar{a} ~ b ~ \bar{c}
 +
\\
 +
\lor & \bar{a} ~ \bar{b} ~ c
 +
\end{matrix}</math>
 +
|-
 +
| height="160px" | [[Image:Cactus (A,(B,C)) Big.jpg|90px]]
 +
| <math>\texttt{(} a \texttt{,(} b \texttt{,} c \texttt{))}</math>
 +
|
 +
<math>\begin{matrix}
 +
\operatorname{oddly~many~of}
 +
\\
 +
a, b, c
 +
\\
 +
\operatorname{are~true}.
 +
\end{matrix}</math>
 +
|
 +
<p><math>a + b + c\!</math></p>
 +
<br>
 +
<p><math>\begin{matrix}
 +
& a ~ b ~ c
 +
\\
 +
\lor & a ~ \bar{b} ~ \bar{c}
 +
\\
 +
\lor & \bar{a} ~ b ~ \bar{c}
 +
\\
 +
\lor & \bar{a} ~ \bar{b} ~ c
 +
\end{matrix}</math></p>
 +
|-
 +
| height="160px" | [[Image:Cactus (X,(A),(B),(C)) Big.jpg|90px]]
 +
| <math>\texttt{(} x \texttt{,(} a \texttt{),(} b \texttt{),(} c \texttt{))}</math>
 +
|
 +
<math>\begin{matrix}
 +
\operatorname{partition}~ x
 +
\\
 +
\operatorname{into}~ a, b, c.
 +
\\[6pt]
 +
\operatorname{genus}~ x ~\operatorname{comprises}
 +
\\
 +
\operatorname{species}~ a, b, c.
 +
\end{matrix}</math>
 +
|
 +
<math>\begin{matrix}
 +
& \bar{x} ~ \bar{a} ~ \bar{b} ~ \bar{c}
 +
\\
 +
\lor & x ~ a ~ \bar{b} ~ \bar{c}
 +
\\
 +
\lor & x ~ \bar{a} ~ b ~ \bar{c}
 +
\\
 +
\lor & x ~ \bar{a} ~ \bar{b} ~ c
 +
\end{matrix}</math>
 +
|}
  
−
The component notation F = <F_1, F_2> = <f, g> : U% -> X% allows
+
<br>
−
us to give a name and a type to this transformation, and permits
 
−
us to define it by means of the compact description that follows:
 
  
−
<x, y>   =  F<u, v>  =   <((u)(v)), ((u, v))>
+
The component notation <math>F = (F_1, F_2) = (f, g) : U^\bullet \to X^\bullet\!</math> allows us to give a name and a type to this transformation, and permits us to define it by means of the compact description that follows:
  
−
The information that defines the logical transformation F
+
{| align="center" cellpadding="8" width="90%"
−
can be represented in the form of a truth table, as below.
+
|
 +
<math>\begin{matrix}
 +
(x, y) & = & F(u, v) & = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ ).
 +
\end{matrix}</math>
 +
|}
  
−
u v | f g
+
The information that defines the logical transformation <math>F\!</math> can be represented in the form of a truth table, as shown below.
−
----+----
 
−
0 0 | 0 1
 
−
0 1 | 1 0
 
−
1 0 | 1 0
 
−
1 1 | 1 1
 
  
−
A more complete framework of discussion and a fuller development of
+
<br>
−
this example can be found in the neighborhood of the following site:
 
  
−
DLOG D73.  http://stderr.org/pipermail/inquiry/2003-June/000557.html
+
{| align="center" cellpadding="8" cellspacing="0" style="border-bottom:1px solid black; border-left:1px solid black; border-right:1px solid black; border-top:1px solid black; text-align:center; width:60%"
−
</pre>
+
|- style="height:40px; background:ghostwhite; width:100%"
 +
| style="width:25%" | <math>u\!</math>
 +
| style="width:25%" | <math>v\!</math>
 +
| style="width:25%; border-left:1px solid black" | <math>f\!</math>
 +
| style="width:25%" | <math>g\!</math>
 +
|-
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
0
 +
\\[4pt]
 +
0
 +
\\[4pt]
 +
1
 +
\\[4pt]
 +
1
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
0
 +
\\[4pt]
 +
1
 +
\\[4pt]
 +
0
 +
\\[4pt]
 +
1
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\begin{matrix}
 +
0
 +
\\[4pt]
 +
1
 +
\\[4pt]
 +
1
 +
\\[4pt]
 +
1
 +
\end{matrix}</math>
 +
| style="border-top:1px solid black" |
 +
<math>\begin{matrix}
 +
1
 +
\\[4pt]
 +
0
 +
\\[4pt]
 +
0
 +
\\[4pt]
 +
1
 +
\end{matrix}</math>
 +
|- style="height:40px; background:ghostwhite"
 +
| style="border-top:1px solid black" | <math>u\!</math>
 +
| style="border-top:1px solid black" | <math>v\!</math>
 +
| style="border-top:1px solid black; border-left:1px solid black" |
 +
<math>\texttt{((} u \texttt{)(} v \texttt{))}\!</math>
 +
| style="border-top:1px solid black" |
 +
<math>\texttt{((} u \texttt{,} v \texttt{))}\!</math>
 +
|}
  
−
==Note 9==
+
<br>
  
−
<pre>
+
A more complete framework of discussion and a fuller development of this example can be found in the neighborhood of the following site:
−
By virtue of Zipf's law -- yes, there is a dynamics to its economics --
 
−
I have found myself forced, when it comes to matters that I've been
 
−
thinking about for "years and years" (YAY) to make a heavy, if not
 
−
to say an overbearing use of acronyms, both for their utility as
 
−
mnemonic devices and as a "regime of code compression" (ROCC).
 
−
I'm well aware that this can be annoying at times, so please
 
−
forgive what I hope will be a transient nuisance and I will
 
−
do my level best to unpack these lexical quanta as we go.
 
  
−
A "moral of the episode" (MOTE) on the wing here:
+
:* [[Differential Logic and Dynamic Systems 2.0#Transformations of Type B2 .E2.86.92 B2|Transformations of Type '''B'''<sup>2</sup> &rarr; '''B'''<sup>2</sup>]]
−
A "transformation of textual elements" (TOTE) is
 
−
a "formal or mathematical abstraction" (FOMA) of
 
−
a very high order, to wit, a "formal object" (FO).
 
  
−
As an object example, let us consider the TOTE in progress:
+
Consider the ''transformation of textual elements'' (TOTE) in progress:
  
−
<x, y>  =   F<u, v>  =   <((u)(v)), ((u, v))>
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{matrix}
 +
x
 +
& = & f(u, v)
 +
& = & \texttt{((} u \texttt{)(} v \texttt{))}
 +
\\[8pt]
 +
y
 +
& = & g(u, v)
 +
& = & \texttt{((} u \texttt{,~} v \texttt{))}
 +
\\[8pt]
 +
(x, y)
 +
& = & F(u, v)
 +
& = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ )
 +
\end{matrix}</math>
 +
|}
  
−
Taken as a transformation from the universe U% = [u, v]
+
Taken as a transformation from the universe <math>U^\bullet = [u, v]\!</math> to the universe <math>X^\bullet = [x, y],\!</math> this is a particular type of formal object, and it can be studied at that level of abstraction until the chickens come home to roost, as they say, but when the time comes to count those chickens, if you will, the terms of artifice that we use to talk about abstract objects, almost as if we actually knew what we were talking about, need to be fully fledged or fleshed out with extra ''bits of interpretive data'' (BOIDs).
−
to the universe X% = [x, y], this is a particular type
 
−
of formal object, and it can be studied at that level
 
−
of abstraction until the chickens come home to roost,
 
−
as they say, but when the time comes to count those
 
−
chickens, if you will, the terms of artifice that
 
−
we use to talk about abstract objects, almost as
 
−
if we actually knew what we were talking about,
 
−
need to be fully fledged or fleshed out with
 
−
extra "bits of interpretive data" (BOID's).
 
  
−
And so, to decompress the story, the TOTE
+
And so, to decompress the story, the TOTE that we use to convey the FOMA has to be interpreted before it can be applied to anything that actually puts supper on the table, so to speak.
−
that we use to convey the FOMA has to be
 
−
interpreted before it can be applied to
 
−
anything that actually puts supper on
 
−
the table, so to speak.
 
  
−
What are some of the ways that an abstract logical transformation
+
What are some of the ways that an abstract logical transformation like <math>F\!</math> gets interpreted in the setting of a concrete application?
−
like F gets interpreted in the setting of a concrete application?
 
  
−
Mathematical parlance comes part way to the rescue here and
+
Mathematical parlance comes part way to the rescue here and tosses us the line that a transformation of syntactic signs can be interpreted in either one of two ways, as an ''alias'' or as an ''alibi''.
−
tosses us the line that a transformation of syntactic signs
 
−
can be interpreted in either one of two ways, as an "alias"
 
−
or as an "alibi".
 
  
−
When we consider a transformation in the alias interpretation,
+
When we consider a transformation in the alias interpretation, we are merely changing the terms that we use to describe what may very well be, to some approximation, the very same things.
−
we are merely changing the terms that we use to describe what
 
−
may very well be, to some approximation, the very same things.
 
  
−
For example, in some applications the discursive universes
+
For example, in some applications the discursive universes <math>U^\bullet = [u, v]\!</math> and <math>X^\bullet = [x, y]\!</math> are best understood as diverse frames, instruments, reticules, scopes, or templates, that we adopt for the sake of viewing from variant perspectives what we conceive to be roughly the same underlying objects.
−
U% = [u, v] and X% = [x, y] are best understood as diverse
 
−
frames, instruments, reticules, scopes, or templates, that
 
−
we adopt for the sake of viewing from variant perspectives
 
−
what we conceive to be roughly the same underlying objects.
 
  
−
When we consider a transformation in the alibi interpretation,
+
When we consider a transformation in the alibi interpretation, we are thinking of the objective things as objectively moving around in space or changing their qualitative characteristics. There are times when we think of this alibi transformation as taking place in a dimension of time, and then there are times when time is not an object.
−
we are thinking of the objective things as objectively moving
 
−
around in space or changing their qualitative characteristics.
 
−
There are times when we think of this alibi transformation as
 
−
taking place in a dimension of time, and then there are times
 
−
when time is not an object.
 
  
−
For example, in some applications the discursive universes
+
For example, in some applications the discursive universes <math>U^\bullet = [u, v]\!</math> and <math>X^\bullet = [x, y]\!</math> are actually the same universe, and what we have is a frame where <math>x\!</math> is the next state of <math>u\!</math> and <math>y\!</math> is the next state of <math>v,\!</math> notated as <math>x = u'\!</math> and <math>y = v'.\!</math>  This permits us to rewrite the transformation <math>F\!</math> as follows:
−
U% = [u, v] and X% = [x, y] are actually the same universe,
 
−
and what we have is a frame where x is the next state of u
 
−
and y is the next state of v, notated as x = u' and y = v'.
 
−
This permits us to rewrite the transformation F as follows:
 
  
−
<u', v'>  =   F<u, v>  =   <((u)(v)), ((u, v))>
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{matrix}
 +
u'
 +
& = & f(u, v)
 +
& = & \texttt{((} u \texttt{)(} v \texttt{))}
 +
\\[8pt]
 +
v'
 +
& = & g(u, v)
 +
& = & \texttt{((} u \texttt{,~} v \texttt{))}
 +
\\[8pt]
 +
(u', v')
 +
& = & F(u, v)
 +
& = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ )
 +
\end{matrix}</math>
 +
|}
  
−
All in all, then, we have three different ways in general
+
All in all, then, we have three different ways in general of applying or interpreting a transformation of discourse, that we might sum up as one brand of alias and two brands of alibi, all together, the ''Elseword'', the ''Elsewhere'', and the ''Elsewhen''.
−
of applying or interpreting a transformation of discourse,
 
−
that we might sum up as one brand of alias and two brands
 
−
of alibi, all together, the Elseword, Elsewhere, Elsewhen.
 
  
−
No more angels on pinheads,
+
No more angels on pinheads, the brass tacks next time.
−
the brass tacks next time.
 
−
</pre>
 
  
−
==Note 10==
+
==Differential Analysis==
  
−
<pre>
+
It is time to formulate the differential analysis of a logical transformation, or a ''mapping of discourse''. It is wise to begin with the first order differentials.
−
It is time to formulate the differential analysis of
 
−
a logical transformation, or a "mapping of discourse".
 
−
It is wise to begin with the first order differentials.
 
  
−
We are considering an abstract logical transformation
+
We are considering an abstract logical transformation <math>F = (f, g) : [u, v] \to [x, y]\!</math> that can be interpreted in a number of different ways.  Let's fix on a couple of major variants that might be indicated as follows:
−
F = <f, g> : [u, v] -> [x, y] that can be interpreted
 
−
in a number of different ways.  Let's fix on a couple
 
−
of major variants that might be indicated as follows:
 
  
−
Alias Map.  <x , y >  = F<u, v>  = <((u)(v)), ((u, v))>
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{lccccc}
 +
\text{Alias Map}
 +
& (x, y)
 +
& = & F(u, v)
 +
& = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ )
 +
\\[8pt]
 +
\text{Alibi Map}
 +
& (u', v')
 +
& = & F(u, v)
 +
& = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ )
 +
\end{array}</math>
 +
|}
  
−
Alibi Map.  <u', v'> =  F<u, v> =  <((u)(v)), ((u, v))>
+
<math>F\!</math> is just one example among &mdash; well, now that I think of it &mdash; how many other logical transformations from the same source to the same target universe?  In the light of that question, maybe it would be advisable to contemplate the character of <math>F\!</math> within the fold of its most closely akin transformations.
  
−
F is just one example among -- well, now that I think of it --
+
Given the alphabets <math>\mathcal{U} = \{ u, v \}\!</math> and <math>\mathcal{X} = \{ x, y \}\!</math> along with the corresponding universes of discourse <math>U^\bullet\!</math> and <math>X^\bullet = [\mathbb{B}^2],\!</math> how many logical transformations of the general form <math>G = (G_1, G_2) : U^\bullet \to X^\bullet\!</math> are there?
−
how many other logical transformations from the same source
 
−
to the same target universe? In the light of that question,
 
−
maybe it would be advisable to contemplate the character of
 
−
F within the fold of its most closely akin transformations.
 
  
−
Given the alphabets !U! = {u, v} and !X! = {x, y},
+
Since <math>G_1\!</math> and <math>G_2\!</math> can be any propositions of the type <math>\mathbb{B}^2 \to \mathbb{B},\!</math> there are <math>2^4 = 16\!</math> choices for each of the maps <math>G_1\!</math> and <math>G_2,\!</math> and thus there are <math>2^4 \cdot 2^4 = 2^8 = 256\!</math> different mappings altogether of the form <math>G : U^\bullet \to X^\bullet.\!</math>
−
along with the corresponding universes of discourse
 
−
U% and X% ~=~ [B^2], how many logical transformations
 
−
of the general form G = <G_1, G_2> : U% -> X% are there?
 
  
−
Since G_1 and G_2 can be any propositions of the type B^2 -> B,
+
The set of all functions of a given type is customarily denoted by placing its type indicator in parentheses, in the present instance writing <math>(U^\bullet \to X^\bullet) = \{ G : U^\bullet \to X^\bullet \},\!</math> and so the cardinality of this ''function space'' can most conveniently be summed up by writing:
−
there are 2^4 = 16 choices for each of the maps G_1 and G_2, and
 
−
thus there are 2^4 * 2^4 = 2^8 = 256 different mappings altogether
 
−
of the form G : U% -> X%.  The set of all functions of a given type
 
−
is customarily denoted by placing its type indicator in parentheses,
 
−
in the present instance writing (U% -> X%) = {G : U% -> X%}, and so
 
−
the cardinality of this "function space" can be most conveniently
 
−
summed up by writing |(U% -> X%)| = |(B^2 -> B^2)| = 4^4 = 256.
 
  
−
Given any transformation of this type, G : U% -> X%, the (first order)
+
{| align="center" cellpadding="8" width="90%"
−
differential analysis of G is based on the definition of a couple of
+
| <math>|(U^\bullet \to X^\bullet)| ~=~ |(\mathbb{B}^2 \to \mathbb{B}^2)| ~=~ 4^4 ~=~ 256.\!</math>
−
further transformations, derived by way of operators on G, that ply
+
|}
−
between the (first order) extended universes, EU% = [u, v, du, dv]
 
−
and EX% = [x, y, dx, dy], of G's own source and target universes.
 
  
−
First, the "enlargement map" (or the "secant transformation")
+
Given any transformation of this type, <math>G : U^\bullet \to X^\bullet,\!</math> the (first order) differential analysis of <math>G\!</math> is based on the definition of a couple of further transformations, derived by way of operators on <math>G,\!</math> that ply between the (first order) extended universes, <math>\mathrm{E}U^\bullet = [u, v, du, dv]\!</math> and <math>\mathrm{E}X^\bullet = [x, y, dx, dy],\!</math> of <math>G\text{'s}\!</math> own source and target universes.
−
EG = <EG_1, EG_2> : EU% -> EX% is defined by the following
 
−
pair of component equations:
 
  
−
EG_1  = G_1 <u + du, v + dv>
+
First, the ''enlargement map'' (or the ''secant transformation'') <math>\mathrm{E}G = (\mathrm{E}G_1, \mathrm{E}G_2) : \mathrm{E}U^\bullet \to \mathrm{E}X^\bullet\!</math> is defined by the following pair of component equations:
  
−
EG_2  = G_2 <u + du, v + dv>
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{lll}
 +
\mathrm{E}G_1
 +
& = & G_1 (u + \mathrm{d}u, v + \mathrm{d}v)
 +
\\[8pt]
 +
\mathrm{E}G_2
 +
& = & G_2 (u + \mathrm{d}u, v + \mathrm{d}v)
 +
\end{array}</math>
 +
|}
  
−
Second, the "difference map" (or the "chordal transformation")
+
Second, the ''difference map'' (or the ''chordal transformation'') <math>{\mathrm{D}G = (\mathrm{D}G_1, \mathrm{D}G_2) : \mathrm{E}U^\bullet \to \mathrm{E}X^\bullet}\!</math> is defined in a component-wise fashion as the boolean sum of the initial proposition <math>G_j\!</math> and the ''enlarged'' or ''shifted'' proposition <math>\mathrm{E}G_j,\!</math> for <math>j = 1, 2,\!</math> in accord with following pair of equations:
−
DG = <DG_1, DG_2> : EU% -> EX% is defined in a component-wise
 
−
fashion as the boolean sum of the initial proposition G_j and
 
−
the enlarged or the "shifted" proposition EG_j, for j = 1, 2,
 
−
in accord with following pair of equations:
 
  
−
DG_1  = G_1 <u, v>  + EG_1 <u, v, du, dv>
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{lllll}
 +
\mathrm{D}G_1
 +
& = & G_1 (u, v)
 +
& + & \mathrm{E}G_1 (u, v, \mathrm{d}u, \mathrm{d}v)
 +
\\[8pt]
 +
& = & G_1 (u, v)
 +
& + & G_1 (u + \mathrm{d}u, v + \mathrm{d}v)
 +
\\[8pt]
 +
\mathrm{D}G_2
 +
& = & G_2 (u, v)
 +
& + & \mathrm{E}G_2 (u, v, \mathrm{d}u, \mathrm{d}v)
 +
\\[8pt]
 +
& = & G_2 (u, v)
 +
& + & G_2 (u + \mathrm{d}u, v + \mathrm{d}v)
 +
\end{array}</math>
 +
|}
  
−
      =  G_1 <u, v> +  G_1 <u + du, v + dv>
+
Maintaining a strict analogy with ordinary difference calculus would perhaps have us write <math>\mathrm{D}G_j = \mathrm{E}G_j - G_j,</math> but the sum and difference operations are the same thing in boolean arithmetic. It is more often natural in the logical context to consider an initial proposition <math>q,\!</math> then to compute the enlargement <math>\mathrm{E}q,</math> and finally to determine the difference <math>\mathrm{D}q = q + \mathrm{E}q,\!</math> so we let the variant order of terms reflect this sequence of considerations.
  
−
DG_2  =  G_2 <u, v> +  EG_2 <u, v, du, dv>
+
Given these general considerations about the operators <math>\mathrm{E}\!</math> and <math>\mathrm{D},\!</math> let's return to particular cases, and carry out the first order analysis of the transformation <math>F(u, v) = ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ ).\!</math>
  
−
      =  G_2 <u, v> +  G_2 <u + du, v + dv>
+
By way of getting our feet back on solid ground, let's crank up our current case of a transformation of discourse, <math>F : U^\bullet \to X^\bullet,\!</math> with concrete type <math>[u, v] \to [x, y]\!</math> or abstract type <math>\mathbb{B}^2 \to \mathbb{B}^2,\!</math> and let it spin through a sufficient number of turns to see how it goes, as viewed under the scope of what is probably its most straightforward view, as an elsewhen map <math>F : [u, v] \to [u', v'].\!</math>
  
−
Maintaining a strict analogy with ordinary difference calculus
+
{| align="center" cellpadding="8" style="text-align:center"
−
would perhaps have us write DG_j = EG_j - G_j, but the sum and
+
|
−
difference operations are the same thing in boolean arithmetic.
+
<math>\begin{array}{ccc}
−
It is more often natural in the logical context to consider an
+
u' & = & \texttt{((} u \texttt{)(} v \texttt{))}
−
initial proposition q, then to compute the enlargement Eq, and
+
\\
−
finally to determine the difference Dq = q + Eq, so we let the
+
v' & = & \texttt{((} u \texttt{,~} v \texttt{))}
−
variant order of terms reflect this sequence of considerations.
+
\end{array}</math>
 +
|-
 +
|
 +
<math>\begin{matrix}
 +
\text{Orbit 1}
 +
\\
 +
\text{Initial Point :}~ (u, v) = (1, 1)
 +
\end{matrix}</math>
 +
|-
 +
|
 +
<math>\begin{array}{c|cc}
 +
t & u & v \\[8pt]
 +
0 & 1 & 1 \\
 +
1 & 1 & 1 \\
 +
2 & {}^\shortparallel & {}^\shortparallel
 +
\end{array}</math>
 +
|-
 +
|
 +
<math>\begin{matrix}
 +
\text{Orbit 2}
 +
\\
 +
\text{Initial Point :}~ (u, v) = (0, 0)
 +
\end{matrix}</math>
 +
|-
 +
|
 +
<math>\begin{array}{c|cc}
 +
t & u & v \\[8pt]
 +
0 & 0 & 0 \\
 +
1 & 0 & 1 \\
 +
2 & 1 & 0 \\
 +
3 & 1 & 0 \\
 +
4 & {}^\shortparallel & {}^\shortparallel
 +
\end{array}</math>
 +
|}
  
−
Given these general considerations about the operators E and D,
+
In the upshot there are two basins of attraction, the state <math>(1, 1)\!</math> and the state <math>(1, 0),\!</math> with the orbit <math>(1, 1)\!</math> making up an isolated basin and the orbit <math>(0, 0), (0, 1), (1, 0)\!</math> leading to the basin <math>(1, 0).\!</math>
−
let's return to particular cases, and carry out the first order
 
−
analysis of the transformation F<u, v> =  <((u)(v)), ((u, v))>.
 
−
</pre>
 
  
−
==Note 11==
+
On first examination of our present example we made a likely guess at a form of rule that would account for the finite protocol of states that we observed the system <math>X\!</math> passing through, as spied in the light of its boolean state variable <math>x : X \to \mathbb{B},\!</math> and that rule is well-formulated in any of these styles of notation:
  
−
<pre>
+
{| align="center" cellpadding="8" width="90%"
−
By way of getting our feet back on solid ground, let's crank up
+
|
−
our current case of a transformation of discourse, F : U% -> X%,
+
<math>\begin{array}{ll}
−
with concrete type [u, v] -> [x, y] or abstract type B^2 -> B^2,
+
1.1. & f : \mathbb{B} \to \mathbb{B} ~\text{such that}~ f : x \mapsto \texttt{(} x \texttt{)}
−
and let it spin through a sufficient number of turns to see how
+
\\
−
it goes, as viewed under the scope of what is probably its most
+
1.2. & x' ~=~ \texttt{(} x \texttt{)}
−
straightforward view, as an elsewhen map F : [u, v] -> [u', v'].
+
\\
 +
1.3. & x ~:=~ \texttt{(} x \texttt{)}
 +
\\
 +
1.4. & \mathrm{d}x ~=~ 1
 +
\end{array}</math>
 +
|}
  
−
Elsewhen Map.  <u', v'>  =  <((u)(v)), ((u, v))>
+
In the current example, we already know in advance the program that generates the state transitions, and it is a rule of the following equivalent and easily derivable forms:
  
−
u v
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{ll}
 +
2.1. & F : \mathbb{B}^2 \to \mathbb{B}^2 ~\text{such that}~ F : (u, v) \mapsto ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ )
 +
\\
 +
2.2. & u' ~=~ \texttt{((} u \texttt{)(} v \texttt{))} \quad ~,~ \quad v' ~=~ \texttt{((} u \texttt{,~} v \texttt{))}
 +
\\
 +
2.3. & u ~:=~ \texttt{((} u \texttt{)(} v \texttt{))} \quad ~,~ \quad v ~:=~ \texttt{((} u \texttt{,~} v \texttt{))}
 +
\\
 +
2.4. & ?
 +
\end{array}</math>
 +
|}
  
−
Incipit 1.  <u, v> = <0, 0>
+
Well, the last one is not such a fall off a log, but that is exactly the purpose for which we have been developing all of the foregoing machinations.
  
−
0 0
+
Here is what I got when I just went ahead and calculated the finite differences willy-nilly:
−
0 1
 
−
1 0
 
−
1 0
 
−
" "
 
  
−
Incipit 2. <u, v> = <1, 1>  
+
{| align="center" cellpadding="8" style="text-align:center"
 +
|-
 +
| <math>\text{Orbit 1. Intitial Point :}~ (u, v) = (1, 1)\!</math>
 +
|-
 +
|
 +
<math>\begin{array}{c|cc|cc|cc|cc|cc|c}
 +
t & u & v & \mathrm{d}u & \mathrm{d}v & \mathrm{d}^2 u & \mathrm{d}^2 v & \mathrm{d}^3 u & \mathrm{d}^3 v & \mathrm{d}^4 u & \mathrm{d}^4 v & \ldots \\[8pt]
 +
0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ldots \\
 +
1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ldots \\
 +
2 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & \ldots
 +
\end{array}</math>
 +
|-
 +
| <math>\text{Orbit 2. Intitial Point :}~ (u, v) = (0, 0)\!</math>
 +
|-
 +
|
 +
<math>\begin{array}{c|cc|cc|cc|cc|cc|c}
 +
t & u & v & \mathrm{d}u & \mathrm{d}v & \mathrm{d}^2 u & \mathrm{d}^2 v & \mathrm{d}^3 u & \mathrm{d}^3 v & \mathrm{d}^4 u & \mathrm{d}^4 v & \ldots \\[8pt]
 +
0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & \ldots \\
 +
1 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & \ldots \\
 +
2 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ldots \\
 +
3 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ldots \\
 +
4 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & \ldots
 +
\end{array}</math>
 +
|}
  
−
1 1
+
To be honest, I have never thought of trying to hack the problem in such a brute-force way until just now, and so I know enough to expect a not inappreciable probability of error about all that I've taken the risk to write out here, but let me forge ahead and see what I can see.
−
1 1
 
−
" "
 
  
−
In fine, there are two basins of attraction,
+
What we are looking for is &mdash; one rule to rule them all, a rule that applies to every state and works every time.
−
the state <1, 0> and the state <1, 1>, with
 
−
the orbit <0, 0>, <0, 1>, <1, 0> leading to
 
−
the first basin and the orbit <1, 1> making
 
−
up an isolated basin.
 
−
</pre>
 
  
−
==Note 12==
+
What we see at first sight in the tables above are patterns of differential features that attach to the states in each orbit of the dynamics.  Looked at locally to these orbits, the isolated fixed point at <math>(1, 1)\!</math> is no problem, as the rule <math>\mathrm{d}u = \mathrm{d}v = 0\!</math> describes it pithily enough.  When it comes to the other orbit, the first thing that comes to mind is to write out the law <math>\mathrm{d}u = v ~,~ \mathrm{d}v = \texttt{(} u \texttt{)}.\!</math>
  
−
<pre>
+
==Symbolic Method==
−
Way back in DATA Note 3, we guessed, or "abduced",
 
−
as a line of logicians from Aristotle to Peirce
 
−
and beyond would say, the form of a rule that
 
−
adequately accounts for the finite protocol
 
−
of states that we observed the system X
 
−
pass through, as spied in the light of
 
−
its boolean state variable x : X -> B,
 
−
and that rule is well-formulated in
 
−
any of these styles of notation:
 
  
−
1.1.  f : B -> B such that f : x ~> (x)
+
It ought to be clear at this point that we need a more systematic symbolic method for computing the differentials of logical transformations, using the term ''differential'' in a loose way at present for all sorts of finite differences and derivatives, leaving it to another discussion to sharpen up its more exact technical senses.
  
−
1.2.  x' = (x)
+
For convenience of reference, let's recast our current example in the following form:
  
−
1.3.  x := (x)
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{matrix}
 +
F & = & (f, g) & = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ ).
 +
\end{matrix}</math>
 +
|}
  
−
1.4. dx =  1
+
In their application to this logical transformation the operators <math>\mathrm{E}\!</math> and <math>\mathrm{D}\!</math> respectively produce the ''enlarged map'' <math>\mathrm{E}F = (\mathrm{E}f, \mathrm{E}g)\!</math> and the ''difference map'' <math>\mathrm{D}F = (\mathrm{D}f, \mathrm{D}g),\!</math> whose components can be given as follows.
  
−
In the current example, having read the manual first,
+
{| align="center" cellpadding="8" width="90%"
−
I guess, we already know in advance the program that
+
|
−
generates the state transitions, and it is a rule of
+
<math>\begin{array}{lll}
−
the following equivalent and easily derivable forms:
+
\mathrm{E}f & = & \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}
 +
\\[8pt]
 +
\mathrm{E}g & = & \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))}
 +
\\[8pt]
 +
\mathrm{D}f & = & \texttt{((} u \texttt{)(} v \texttt{))} ~+~ \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}
 +
\\[8pt]
 +
\mathrm{D}g & = & \texttt{((} u \texttt{,~} v \texttt{))} ~+~ \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))}
 +
\end{array}</math>
 +
|}
  
−
2.1.  F : B^2 -> B^2 such that F : <u, v> ~> <((u)(v)), ((u, v))>
+
But these initial formulas are purely definitional, and help us little to understand either the purpose of the operators or the significance of the results.  Working symbolically, let's apply a more systematic method to the separate components of the mapping <math>F.\!</math>
  
−
2.2.  u' = ((u)(v)),  v' = ((u, v))
+
A sketch of this work is presented in the following series of Figures, where each logical proposition is expanded over the basic cells <math>uv, u \texttt{(} v \texttt{)}, \texttt{(} u \texttt{)} v, \texttt{(} u \texttt{)(} v \texttt{)}\!</math> of the 2-dimensional universe of discourse <math>U^\bullet = [u, v].\!</math>
  
−
2.3.  u := ((u)(v)),  v := ((u, v))
+
===Computation Summary for Logical Disjunction===
  
−
2.4.  ???
+
The venn diagram in Figure&nbsp;1.1 shows how the proposition <math>f = \texttt{((} u \texttt{)(} v \texttt{))}\!</math> can be expanded over the universe of discourse <math>[u, v]\!</math> to produce a logically equivalent exclusive disjunction, namely, <math>uv + u \texttt{(} v \texttt{)} + \texttt{(} u \texttt{)} v.\!</math>
−
 
 
−
Well, the last one is not such a fall off the log,
 
−
but that is exactly the purpose for which we have
 
−
been developing all of the foregoing machinations.
 
−
 
 
−
Here is what I got when I just went ahead and
 
−
calculated the finite differences willy-nilly:
 
−
 
 
−
Incipit 1.  <u, v> = <0, 0>  
 
−
o-----o-----o-----o-----o-----o-----o
 
−
| d d | d d | d d | d d | d d | ... |
 
−
| 0 0 | 1 1 | 2 2 | 3 3 | 4 4 | ... |
 
−
| u v | u v | u v | u v | u v | ... |
 
−
o-----o-----o-----o-----o-----o-----o
 
−
| 0 0 | 0 1 | 1 0 | 0 1 | 1 0 | ... |
 
−
| 0 1 | 1 1 | 1 1 | 1 1 | 1 1 | ... |
 
−
| 1 0 | 0 0 | 0 0 | 0 0 | 0 0 | ... |
 
−
| 1 0 | 0 0 | 0 0 | 0 0 | 0 0 | ... |
 
−
| " " | " " | " " | " " | " " | """ |
 
−
o-----o-----o-----o-----o-----o-----o
 
−
 
 
−
Incipit 2.  <u, v> = <1, 1>  
 
−
o-----o-----o-----o-----o
 
−
| d d | d d | d d | d d |
 
−
| 0 0 | 1 1 | 2 2 | 3 3 |
 
−
| u v | u v | u v | u v |
 
−
o-----o-----o-----o-----o
 
−
| 1 1 | 0 0 | 0 0 | = = |
 
−
| 1 1 | 0 0 | 0 0 | = = |
 
−
| " " | " " | " " | " " |
 
−
o-----o-----o-----o-----o
 
−
 
 
−
To be honest, I have never thought of trying
 
−
to hack the problem in such a brute-force way
 
−
until just now, and so I know enough to expect
 
−
a not unappreciable probability of error about
 
−
all that I've taken the risk to write out here,
 
−
but let me forge ahead and see what I can see.
 
−
 
 
−
What we are looking for is -- one rule to rule them all,
 
−
a rule that applies to every state and works every time.
 
−
 
 
−
What we see at first sight in the tables above are patterns
 
−
of differential features that attach to the states in each
 
−
orbit of the dynamics.  Looked at locally to these orbits,
 
−
the isolated fixed point at <1, 1> is no problem, as the
 
−
rule du = dv = 0 describes it pithily enough.  When it
 
−
comes to the other orbit, the first thing that comes
 
−
to mind is to write out the law du = v, dv = (u).
 
−
 
 
−
I am going to take a nap to clear my head.
 
−
</pre>
 
−
 
 
−
==Note 13==
 
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 
<pre>
 
<pre>
−
I think that it ought to be clear at this point that we
 
−
need a more systematic symbolic method for computing the
 
−
differentials of logical transformations, using the term
 
−
"differential" in a loose way at present for all sorts of
 
−
finite differences and derivatives, leaving it to another
 
−
discussion to sharpen up its more exact technical senses.
 
−
 
−
For convenience of reference, let's recast our current
 
−
example in the form F = <f, g> = <((u)(v)), ((u, v))>.
 
−
 
−
In their application to this logical transformation the operators
 
−
E and D respectively produce the "enlarged map" EF = <Ef, Eg> and
 
−
the "difference map" DF = <Df, Dg>, whose components can be given
 
−
as follows, if the reader, in the absence of a special format for
 
−
logical parentheses, can forgive syntactically 2-lingual phrases:
 
−
 
−
Ef  =  ((u + du)(v + dv))
 
−
 
−
Eg  =  ((u + du, v + dv))
 
−
 
−
Df  =  ((u)(v))  +  ((u + du)(v + dv))
 
−
 
−
Dg  =  ((u, v))  +  ((u + du, v + dv))
 
−
 
−
But these initial formulas are purely definitional,
 
−
and help us little to understand either the purpose
 
−
of the operators or the significance of the results.
 
−
Working symbolically, let's apply a more systematic
 
−
method to the separate components of the mapping F.
 
−
 
−
A sketch of this work is presented in the following series
 
−
of Figures, where each logical proposition is expanded over
 
−
the basic cells uv, u(v), (u)v, (u)(v) of the 2-dimensional
 
−
universe of discourse U% = [u, v].
 
−
 
−
Computation Summary for f<u, v> = ((u)(v))
 
−
 
−
Figure 1.1 expands f = ((u)(v)) over [u, v] to produce
 
−
the equivalent exclusive disjunction uv + u(v) + (u)v.
 
−
 
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/%\``````````````````|
+
|                 /%\                 |
−
|`````````````````/%%%\`````````````````|
+
|                 /%%%\                 |
−
|````````````````/%%%%%\````````````````|
+
|               /%%%%%\               |
−
|```````````````o%%%%%%%o```````````````|
+
|               o%%%%%%%o               |
−
|``````````````/%\%%%%%/%\``````````````|
+
|             /%\%%%%%/%\             |
−
|`````````````/%%%\%%%/%%%\`````````````|
+
|             /%%%\%%%/%%%\             |
−
|````````````/%%%%%\%/%%%%%\````````````|
+
|           /%%%%%\%/%%%%%\           |
−
|```````````o%%%%%%%o%%%%%%%o```````````|
+
|           o%%%%%%%o%%%%%%%o           |
−
|``````````/%\%%%%%/%\%%%%%/%\``````````|
+
|         /%\%%%%%/%\%%%%%/%\         |
−
|`````````/%%%\%%%/%%%\%%%/%%%\`````````|
+
|         /%%%\%%%/%%%\%%%/%%%\         |
−
|````````/%%%%%\%/%%%%%\%/%%%%%\````````|
+
|       /%%%%%\%/%%%%%\%/%%%%%\       |
−
|```````o%%%%%%%o%%%%%%%o%%%%%%%o```````|
+
|       o%%%%%%%o%%%%%%%o%%%%%%%o       |
−
|``````/%\%%%%%/%\%%%%%/%\%%%%%/%\``````|
+
|     /%\%%%%%/%\%%%%%/%\%%%%%/%\     |
−
|`````/%%%\%%%/%%%\%%%/%%%\%%%/%%%\`````|
+
|     /%%%\%%%/%%%\%%%/%%%\%%%/%%%\     |
−
|````/%%%%%\%/%%%%%\%/%%%%%\%/%%%%%\````|
+
|   /%%%%%\%/%%%%%\%/%%%%%\%/%%%%%\   |
−
|```o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o```|
+
|   o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o   |
−
|```|\%%%%%/%\%%%%%/`\%%%%%/%\%%%%%/|```|
+
|   |\%%%%%/%\%%%%%/ \%%%%%/%\%%%%%/|   |
−
|```|`\%%%/%%%\%%%/```\%%%/%%%\%%%/`|```|
+
|   | \%%%/%%%\%%%/   \%%%/%%%\%%%/ |   |
−
|```|``\%/%%%%%\%/`````\%/%%%%%\%/``|```|
+
|   | \%/%%%%%\%/     \%/%%%%%\%/ |   |
−
|```|```o%%%%%%%o```````o%%%%%%%o```|```|
+
|   |   o%%%%%%%o       o%%%%%%%o   |   |
−
|```|```|\%%%%%/`\`````/`\%%%%%/|```|```|
+
|   |   |\%%%%%/ \     / \%%%%%/|   |   |
−
|```|```|`\%%%/```\```/```\%%%/`|```|```|
+
|   |   | \%%%/   \   /   \%%%/ |   |   |
−
|```|`u`|``\%/`````\`/`````\%/``|`v`|```|
+
|   | u | \%/     \ /     \%/ | v |   |
−
|```o---+---o```````o```````o---+---o```|
+
|   o---+---o       o       o---+---o   |
−
|```````|````\`````/`\`````/````|```````|
+
|       |   \     / \     /   |       |
−
|```````|`````\```/```\```/`````|```````|
+
|       |     \   /   \   /     |       |
−
|```````|`du```\`/`````\`/```dv`|```````|
+
|       | du   \ /     \ /   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 1.1.  f = ((u)(v))
 
Figure 1.1.  f = ((u)(v))
 +
</pre>
 +
|}
  
−
Figure 1.2 expands Ef = ((u + du)(v + dv)) over [u, v] to give:
+
Figure&nbsp;1.2 expands <math>\mathrm{E}f = \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}\!</math> over <math>[u, v]\!</math> to give:
  
−
uv.(du dv) + u(v).(du (dv)) + (u)v.((du) dv) + (u)(v).((du)(dv))
+
{| align="center" cellpadding="8" style="text-align:center; width:100%"
 +
|
 +
<math>\begin{matrix}
 +
\mathrm{E}\texttt{((} u \texttt{)(} v \texttt{))}
 +
& = & uv \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))}
 +
& + & \texttt{(} u \texttt{)} v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
\end{matrix}</math>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/%\``````````````````|
+
|                 /%\                 |
−
|`````````````````/%%%\`````````````````|
+
|                 /%%%\                 |
−
|````````````````/%%%%%\````````````````|
+
|               /%%%%%\               |
−
|```````````````o%%%%%%%o```````````````|
+
|               o%%%%%%%o               |
−
|``````````````/%\%%%%%/%\``````````````|
+
|             /%\%%%%%/%\             |
−
|`````````````/%%%\%%%/%%%\`````````````|
+
|             /%%%\%%%/%%%\             |
−
|````````````/%%%%%\%/%%%%%\````````````|
+
|           /%%%%%\%/%%%%%\           |
−
|```````````o%%%%%%%o%%%%%%%o```````````|
+
|           o%%%%%%%o%%%%%%%o           |
−
|``````````/%\%%%%%/`\%%%%%/%\``````````|
+
|         /%\%%%%%/ \%%%%%/%\         |
−
|`````````/%%%\%%%/```\%%%/%%%\`````````|
+
|         /%%%\%%%/   \%%%/%%%\         |
−
|````````/%%%%%\%/`````\%/%%%%%\````````|
+
|       /%%%%%\%/     \%/%%%%%\       |
−
|```````o%%%%%%%o```````o%%%%%%%o```````|
+
|       o%%%%%%%o       o%%%%%%%o       |
−
|``````/%\%%%%%/%\`````/%\%%%%%/%\``````|
+
|     /%\%%%%%/%\     /%\%%%%%/%\     |
−
|`````/%%%\%%%/%%%\```/%%%\%%%/%%%\`````|
+
|     /%%%\%%%/%%%\   /%%%\%%%/%%%\     |
−
|````/%%%%%\%/%%%%%\`/%%%%%\%/%%%%%\````|
+
|   /%%%%%\%/%%%%%\ /%%%%%\%/%%%%%\   |
−
|```o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o```|
+
|   o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o   |
−
|```|\%%%%%/`\%%%%%/%\%%%%%/`\%%%%%/|```|
+
|   |\%%%%%/ \%%%%%/%\%%%%%/ \%%%%%/|   |
−
|```|`\%%%/```\%%%/%%%\%%%/```\%%%/`|```|
+
|   | \%%%/   \%%%/%%%\%%%/   \%%%/ |   |
−
|```|``\%/`````\%/%%%%%\%/`````\%/``|```|
+
|   | \%/     \%/%%%%%\%/     \%/ |   |
−
|```|```o```````o%%%%%%%o```````o```|```|
+
|   |   o       o%%%%%%%o       o   |   |
−
|```|```|\`````/%\%%%%%/%\`````/|```|```|
+
|   |   |\     /%\%%%%%/%\     /|   |   |
−
|```|```|`\```/%%%\%%%/%%%\```/`|```|```|
+
|   |   | \   /%%%\%%%/%%%\   / |   |   |
−
|```|`u`|``\`/%%%%%\%/%%%%%\`/``|`v`|```|
+
|   | u | \ /%%%%%\%/%%%%%\ / | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/`\%%%%%/````|```````|
+
|       |   \%%%%%/ \%%%%%/   |       |
−
|```````|`````\%%%/```\%%%/`````|```````|
+
|       |     \%%%/   \%%%/     |       |
−
|```````|`du```\%/`````\%/```dv`|```````|
+
|       | du   \%/     \%/   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 1.2.  Ef = ((u + du)(v + dv))
 
Figure 1.2.  Ef = ((u + du)(v + dv))
 +
</pre>
 +
|}
  
−
Figure 1.3 expands Df = f + Ef over [u, v] to produce:
+
Figure&nbsp;1.3 expands <math>\mathrm{D}f = f + \mathrm{E}f\!</math> over <math>[u, v]\!</math> to produce:
  
−
uv.du dv + u(v).du(dv) + (u)v.(du)dv + (u)(v).((du)(dv))
+
{| align="center" cellpadding="8" style="text-align:center; width:100%"
 +
|
 +
<math>\begin{matrix}
 +
\mathrm{D}\texttt{((} u \texttt{)(} v \texttt{))}
 +
& = & uv \cdot \mathrm{d}u ~ \mathrm{d}v
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
\end{matrix}</math>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/`\``````````````````|
+
|                 / \                 |
−
|`````````````````/```\`````````````````|
+
|                 /   \                 |
−
|````````````````/`````\````````````````|
+
|               /     \               |
−
|```````````````o```````o```````````````|
+
|               o       o               |
−
|``````````````/`\`````/`\``````````````|
+
|             / \     / \             |
−
|`````````````/```\```/```\`````````````|
+
|             /   \   /   \             |
−
|````````````/`````\`/`````\````````````|
+
|           /     \ /     \           |
−
|```````````o```````o```````o```````````|
+
|           o       o       o           |
−
|``````````/`\`````/%\`````/`\``````````|
+
|         / \     /%\     / \         |
−
|`````````/```\```/%%%\```/```\`````````|
+
|         /   \   /%%%\   /   \         |
−
|````````/`````\`/%%%%%\`/`````\````````|
+
|       /     \ /%%%%%\ /     \       |
−
|```````o```````o%%%%%%%o```````o```````|
+
|       o       o%%%%%%%o       o       |
−
|``````/`\`````/`\%%%%%/`\`````/`\``````|
+
|     / \     / \%%%%%/ \     / \     |
−
|`````/```\```/```\%%%/```\```/```\`````|
+
|     /   \   /   \%%%/   \   /   \     |
−
|````/`````\`/`````\%/`````\`/`````\````|
+
|   /     \ /     \%/     \ /     \   |
−
|```o```````o```````o```````o```````o```|
+
|   o       o       o       o       o   |
−
|```|\`````/%\`````/%\`````/%\`````/|```|
+
|   |\     /%\     /%\     /%\     /|   |
−
|```|`\```/%%%\```/%%%\```/%%%\```/`|```|
+
|   | \   /%%%\   /%%%\   /%%%\   / |   |
−
|```|``\`/%%%%%\`/%%%%%\`/%%%%%\`/``|```|
+
|   | \ /%%%%%\ /%%%%%\ /%%%%%\ / |   |
−
|```|```o%%%%%%%o%%%%%%%o%%%%%%%o```|```|
+
|   |   o%%%%%%%o%%%%%%%o%%%%%%%o   |   |
−
|```|```|\%%%%%/%\%%%%%/%\%%%%%/|```|```|
+
|   |   |\%%%%%/%\%%%%%/%\%%%%%/|   |   |
−
|```|```|`\%%%/%%%\%%%/%%%\%%%/`|```|```|
+
|   |   | \%%%/%%%\%%%/%%%\%%%/ |   |   |
−
|```|`u`|``\%/%%%%%\%/%%%%%\%/``|`v`|```|
+
|   | u | \%/%%%%%\%/%%%%%\%/ | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/`\%%%%%/````|```````|
+
|       |   \%%%%%/ \%%%%%/   |       |
−
|```````|`````\%%%/```\%%%/`````|```````|
+
|       |     \%%%/   \%%%/     |       |
−
|```````|`du```\%/`````\%/```dv`|```````|
+
|       | du   \%/     \%/   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 1.3.  Df = f + Ef
 
Figure 1.3.  Df = f + Ef
−
 
−
I'll break this here in case anyone wants
 
−
to try and do the work for g on their own.
 
 
</pre>
 
</pre>
 +
|}
  
−
==Note 14==
+
I'll break this here in case anyone wants to try and do the work for <math>g\!</math> on their own.
  
−
<pre>
+
===Computation Summary for Logical Equality===
−
No doubt everybody who's still awake sacrificed
 
−
the few spare moments of their sleep last night
 
−
that it took to Figure all this out already,
 
−
but just for the record here's what I got:
 
  
−
Computation Summary for g<u, v> = ((u, v))
+
The venn diagram in Figure&nbsp;2.1 shows how the proposition <math>g = \texttt{((} u \texttt{,~} v \texttt{))}\!</math> can be expanded over the universe of discourse <math>[u, v]\!</math> to produce a logically equivalent exclusive disjunction, namely, <math>uv + \texttt{(} u \texttt{)(} v \texttt{)}.\!</math>
−
 
 
−
Figure 2.1 expands g = ((u, v)) over [u, v] into
 
−
the equivalent exclusive disjunction uv + (u)(v).
 
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/%\``````````````````|
+
|                 /%\                 |
−
|`````````````````/%%%\`````````````````|
+
|                 /%%%\                 |
−
|````````````````/%%%%%\````````````````|
+
|               /%%%%%\               |
−
|```````````````o%%%%%%%o```````````````|
+
|               o%%%%%%%o               |
−
|``````````````/%\%%%%%/%\``````````````|
+
|             /%\%%%%%/%\             |
−
|`````````````/%%%\%%%/%%%\`````````````|
+
|             /%%%\%%%/%%%\             |
−
|````````````/%%%%%\%/%%%%%\````````````|
+
|           /%%%%%\%/%%%%%\           |
−
|```````````o%%%%%%%o%%%%%%%o```````````|
+
|           o%%%%%%%o%%%%%%%o           |
−
|``````````/`\%%%%%/%\%%%%%/`\``````````|
+
|         / \%%%%%/%\%%%%%/ \         |
−
|`````````/```\%%%/%%%\%%%/```\`````````|
+
|         /   \%%%/%%%\%%%/   \         |
−
|````````/`````\%/%%%%%\%/`````\````````|
+
|       /     \%/%%%%%\%/     \       |
−
|```````o```````o%%%%%%%o```````o```````|
+
|       o       o%%%%%%%o       o       |
−
|``````/`\`````/`\%%%%%/`\`````/`\``````|
+
|     / \     / \%%%%%/ \     / \     |
−
|`````/```\```/```\%%%/```\```/```\`````|
+
|     /   \   /   \%%%/   \   /   \     |
−
|````/`````\`/`````\%/`````\`/`````\````|
+
|   /     \ /     \%/     \ /     \   |
−
|```o```````o```````o```````o```````o```|
+
|   o       o       o       o       o   |
−
|```|\`````/`\`````/%\`````/`\`````/|```|
+
|   |\     / \     /%\     / \     /|   |
−
|```|`\```/```\```/%%%\```/```\```/`|```|
+
|   | \   /   \   /%%%\   /   \   / |   |
−
|```|``\`/`````\`/%%%%%\`/`````\`/``|```|
+
|   | \ /     \ /%%%%%\ /     \ / |   |
−
|```|```o```````o%%%%%%%o```````o```|```|
+
|   |   o       o%%%%%%%o       o   |   |
−
|```|```|\`````/%\%%%%%/%\`````/|```|```|
+
|   |   |\     /%\%%%%%/%\     /|   |   |
−
|```|```|`\```/%%%\%%%/%%%\```/`|```|```|
+
|   |   | \   /%%%\%%%/%%%\   / |   |   |
−
|```|`u`|``\`/%%%%%\%/%%%%%\`/``|`v`|```|
+
|   | u | \ /%%%%%\%/%%%%%\ / | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/%\%%%%%/````|```````|
+
|       |   \%%%%%/%\%%%%%/   |       |
−
|```````|`````\%%%/%%%\%%%/`````|```````|
+
|       |     \%%%/%%%\%%%/     |       |
−
|```````|`du```\%/%%%%%\%/```dv`|```````|
+
|       | du   \%/%%%%%\%/   dv |       |
−
|```````o-------o%%%%%%%o-------o```````|
+
|       o-------o%%%%%%%o-------o       |
−
|````````````````\%%%%%/````````````````|
+
|               \%%%%%/               |
−
|`````````````````\%%%/`````````````````|
+
|                 \%%%/                 |
−
|``````````````````\%/``````````````````|
+
|                 \%/                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 2.1.  g = ((u, v))
 
Figure 2.1.  g = ((u, v))
 +
</pre>
 +
|}
  
−
Figure 2.2 expands Eg = ((u + du, v + dv)) over [u, v] to give:
+
Figure&nbsp;2.2 expands <math>\mathrm{E}g = \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))}\!</math> over <math>[u, v]\!</math> to give:
  
−
uv.((du, dv)) + u(v).(du, dv) + (u)v.(du, dv) + (u)(v).((du, dv))
+
{| align="center" cellpadding="8" style="text-align:center; width:100%"
 +
|
 +
<math>\begin{matrix}
 +
\mathrm{E}\texttt{((} u \texttt{,~} v \texttt{))}
 +
& = & uv \cdot \texttt{((} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{))}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{))}
 +
\end{matrix}</math>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/%\``````````````````|
+
|                 /%\                 |
−
|`````````````````/%%%\`````````````````|
+
|                 /%%%\                 |
−
|````````````````/%%%%%\````````````````|
+
|               /%%%%%\               |
−
|```````````````o%%%%%%%o```````````````|
+
|               o%%%%%%%o               |
−
|``````````````/`\%%%%%/`\``````````````|
+
|             / \%%%%%/ \             |
−
|`````````````/```\%%%/```\`````````````|
+
|             /   \%%%/   \             |
−
|````````````/`````\%/`````\````````````|
+
|           /     \%/     \           |
−
|```````````o```````o```````o```````````|
+
|           o       o       o           |
−
|``````````/%\`````/%\`````/%\``````````|
+
|         /%\     /%\     /%\         |
−
|`````````/%%%\```/%%%\```/%%%\`````````|
+
|         /%%%\   /%%%\   /%%%\         |
−
|````````/%%%%%\`/%%%%%\`/%%%%%\````````|
+
|       /%%%%%\ /%%%%%\ /%%%%%\       |
−
|```````o%%%%%%%o%%%%%%%o%%%%%%%o```````|
+
|       o%%%%%%%o%%%%%%%o%%%%%%%o       |
−
|``````/`\%%%%%/`\%%%%%/`\%%%%%/`\``````|
+
|     / \%%%%%/ \%%%%%/ \%%%%%/ \     |
−
|`````/```\%%%/```\%%%/```\%%%/```\`````|
+
|     /   \%%%/   \%%%/   \%%%/   \     |
−
|````/`````\%/`````\%/`````\%/`````\````|
+
|   /     \%/     \%/     \%/     \   |
−
|```o```````o```````o```````o```````o```|
+
|   o       o       o       o       o   |
−
|```|\`````/%\`````/%\`````/%\`````/|```|
+
|   |\     /%\     /%\     /%\     /|   |
−
|```|`\```/%%%\```/%%%\```/%%%\```/`|```|
+
|   | \   /%%%\   /%%%\   /%%%\   / |   |
−
|```|``\`/%%%%%\`/%%%%%\`/%%%%%\`/``|```|
+
|   | \ /%%%%%\ /%%%%%\ /%%%%%\ / |   |
−
|```|```o%%%%%%%o%%%%%%%o%%%%%%%o```|```|
+
|   |   o%%%%%%%o%%%%%%%o%%%%%%%o   |   |
−
|```|```|\%%%%%/`\%%%%%/`\%%%%%/|```|```|
+
|   |   |\%%%%%/ \%%%%%/ \%%%%%/|   |   |
−
|```|```|`\%%%/```\%%%/```\%%%/`|```|```|
+
|   |   | \%%%/   \%%%/   \%%%/ |   |   |
−
|```|`u`|``\%/`````\%/`````\%/``|`v`|```|
+
|   | u | \%/     \%/     \%/ | v |   |
−
|```o---+---o```````o```````o---+---o```|
+
|   o---+---o       o       o---+---o   |
−
|```````|````\`````/%\`````/````|```````|
+
|       |   \     /%\     /   |       |
−
|```````|`````\```/%%%\```/`````|```````|
+
|       |     \   /%%%\   /     |       |
−
|```````|`du```\`/%%%%%\`/```dv`|```````|
+
|       | du   \ /%%%%%\ /   dv |       |
−
|```````o-------o%%%%%%%o-------o```````|
+
|       o-------o%%%%%%%o-------o       |
−
|````````````````\%%%%%/````````````````|
+
|               \%%%%%/               |
−
|`````````````````\%%%/`````````````````|
+
|                 \%%%/                 |
−
|``````````````````\%/``````````````````|
+
|                 \%/                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 2.2.  Eg = ((u + du, v + dv))
 
Figure 2.2.  Eg = ((u + du, v + dv))
 +
</pre>
 +
|}
  
−
Figure 2.3 expands Dg = g + Eg over [u, v] to yield the form:
+
Figure&nbsp;2.3 expands <math>\mathrm{D}g = g + \mathrm{E}g\!</math> over <math>[u, v]\!</math> to yield the form:
  
−
uv.(du, dv) + u(v).(du, dv) + (u)v.(du, dv) + (u)(v).(du, dv)
+
{| align="center" cellpadding="8" style="text-align:center; width:100%"
 +
|
 +
<math>\begin{matrix}
 +
\mathrm{D}\texttt{((} u \texttt{,~} v \texttt{))}
 +
& = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
 +
\end{matrix}</math>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/`\``````````````````|
+
|                 / \                 |
−
|`````````````````/```\`````````````````|
+
|                 /   \                 |
−
|````````````````/`````\````````````````|
+
|               /     \               |
−
|```````````````o```````o```````````````|
+
|               o       o               |
−
|``````````````/%\`````/%\``````````````|
+
|             /%\     /%\             |
−
|`````````````/%%%\```/%%%\`````````````|
+
|             /%%%\   /%%%\             |
−
|````````````/%%%%%\`/%%%%%\````````````|
+
|           /%%%%%\ /%%%%%\           |
−
|```````````o%%%%%%%o%%%%%%%o```````````|
+
|           o%%%%%%%o%%%%%%%o           |
−
|``````````/%\%%%%%/`\%%%%%/%\``````````|
+
|         /%\%%%%%/ \%%%%%/%\         |
−
|`````````/%%%\%%%/```\%%%/%%%\`````````|
+
|         /%%%\%%%/   \%%%/%%%\         |
−
|````````/%%%%%\%/`````\%/%%%%%\````````|
+
|       /%%%%%\%/     \%/%%%%%\       |
−
|```````o%%%%%%%o```````o%%%%%%%o```````|
+
|       o%%%%%%%o       o%%%%%%%o       |
−
|``````/`\%%%%%/`\`````/`\%%%%%/`\``````|
+
|     / \%%%%%/ \     / \%%%%%/ \     |
−
|`````/```\%%%/```\```/```\%%%/```\`````|
+
|     /   \%%%/   \   /   \%%%/   \     |
−
|````/`````\%/`````\`/`````\%/`````\````|
+
|   /     \%/     \ /     \%/     \   |
−
|```o```````o```````o```````o```````o```|
+
|   o       o       o       o       o   |
−
|```|\`````/%\`````/`\`````/%\`````/|```|
+
|   |\     /%\     / \     /%\     /|   |
−
|```|`\```/%%%\```/```\```/%%%\```/`|```|
+
|   | \   /%%%\   /   \   /%%%\   / |   |
−
|```|``\`/%%%%%\`/`````\`/%%%%%\`/``|```|
+
|   | \ /%%%%%\ /     \ /%%%%%\ / |   |
−
|```|```o%%%%%%%o```````o%%%%%%%o```|```|
+
|   |   o%%%%%%%o       o%%%%%%%o   |   |
−
|```|```|\%%%%%/%\`````/%\%%%%%/|```|```|
+
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
−
|```|```|`\%%%/%%%\```/%%%\%%%/`|```|```|
+
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
−
|```|`u`|``\%/%%%%%\`/%%%%%\%/``|`v`|```|
+
|   | u | \%/%%%%%\ /%%%%%\%/ | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/`\%%%%%/````|```````|
+
|       |   \%%%%%/ \%%%%%/   |       |
−
|```````|`````\%%%/```\%%%/`````|```````|
+
|       |     \%%%/   \%%%/     |       |
−
|```````|`du```\%/`````\%/```dv`|```````|
+
|       | du   \%/     \%/   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 2.3.  Dg = g + Eg
 
Figure 2.3.  Dg = g + Eg
 
</pre>
 
</pre>
 +
|}
  
−
==Note 15==
+
==Differential : Locally Linear Approximation==
  
−
<pre>
+
{| cellpadding="2" cellspacing="2" width="100%"
−
| 'Tis a derivative from me to mine,
+
| width="60%" | &nbsp;
−
|  And only that I stand for.
+
| width="40%" |
−
|
+
'Tis a derivative from me to mine,<br>
−
| Winter's Tale, 3.2.43-44
+
And only that I stand for.
 +
|-
 +
| height="50px" | &nbsp;
 +
| valign="top"  | &mdash; ''Winter's Tale'', 3.2.43&ndash;44
 +
|}
  
−
We've talked about differentials long enough
+
We've talked about differentials long enough that I think it's way past time we met with some.
−
that I think it's past time we met with some.
 
  
−
When the term is being used with its more exact sense,
+
When the term is being used with its more exact sense, a ''differential'' is a locally linear approximation to a function, in the context of this logical discussion, then, a locally linear approximation to a proposition.
−
a "differential" is a locally linear approximation to
 
−
a function, in the context of this logical discussion,
 
−
then, a locally linear approximation to a proposition.
 
  
−
I think that it would be best to just go ahead and
+
Recall the form of the current example:
−
exhibit the simplest form of a differential dF for
 
−
the current example of a logical transformation F,
 
−
after which the majority of the easiest questions
 
−
will've been answered in visually intuitive terms.
 
  
−
For F = <f, g> we have dF = <df, dg>, and so we can proceed
+
{| align="center" cellpadding="8" width="90%"
−
componentwise, patching the pieces back together at the end.
+
|
 +
<math>\begin{array}{lllll}
 +
F
 +
& = & (f, g)
 +
& = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ )
 +
\end{array}</math>
 +
|}
  
−
We have prepared the ground already by computing these terms:
+
To speed things along, I will skip a mass of motivating discussion and just exhibit the simplest form of a differential <math>\mathrm{d}F\!</math> for the current example of a logical transformation <math>F,\!</math> after which the majority of the easiest questions will have been answered in visually intuitive terms.
  
−
Ef  = ((u + du)(v + dv))
+
For <math>F = (f, g)\!</math> we have <math>\mathrm{d}F = (\mathrm{d}f, \mathrm{d}g),\!</math> and so we can proceed componentwise, patching the pieces back together at the end.
  
−
Eg  =  ((u + du, v + dv))
+
We have prepared the ground already by computing these terms:
  
−
Df  = ((u)(v)) + ((u + du)(v + dv))
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{lll}
 +
\mathrm{E}f & = & \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}
 +
\\[8pt]
 +
\mathrm{E}g & = & \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))}
 +
\\[8pt]
 +
\mathrm{D}f & = & \texttt{((} u \texttt{)(} v \texttt{))} ~+~ \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}
 +
\\[8pt]
 +
\mathrm{D}g & = & \texttt{((} u \texttt{,~} v \texttt{))} ~+~ \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))}
 +
\end{array}</math>
 +
|}
  
−
Dg  =  ((u, v))  +  ((u + du, v + dv))
+
As a matter of fact, computing the symmetric differences <math>\mathrm{D}f = f + \mathrm{E}f\!</math> and <math>\mathrm{D}g = g + \mathrm{E}g\!</math> has already taken care of the ''localizing'' part of the task by subtracting out the forms of <math>f\!</math> and <math>g\!</math> from the forms of <math>\mathrm{E}f\!</math> and <math>\mathrm{E}g,\!</math> respectively.  Thus all we have left to do is to decide what linear propositions best approximate the difference maps <math>{\mathrm{D}f}\!</math> and <math>{\mathrm{D}g},\!</math> respectively.
−
 
 
−
As a matter of fact, computing the symmetric differences
 
−
Df = f + Ef and Dg = g + Eg has already taken care of the
 
−
"localizing" part of the task by subtracting out the forms
 
−
of f and g from the forms of Ef and Eg, respectively.  Thus
 
−
all we have left to do is to decide what linear propositions
 
−
best approximate the difference maps Df and Dg, respectively.
 
  
 
This raises the question:  What is a linear proposition?
 
This raises the question:  What is a linear proposition?
  
−
The answer that makes the most sense in this context is this:
+
The answer that makes the most sense in this context is this: A proposition is just a boolean-valued function, so a linear proposition is a linear function into the boolean space <math>\mathbb{B}.\!</math>
−
A proposition is just a boolean-valued function, so a linear
 
−
proposition is a linear function into the boolean space B.
 
  
−
In particular, the linear functions that we want will be
+
In particular, the linear functions that we want will be linear functions in the differential variables <math>\mathrm{d}u\!</math> and <math>\mathrm{d}v.\!</math>
−
linear functions in the differential variables du and dv.
 
  
−
As it turns out, there are just four linear propositions
+
As it turns out, there are just four linear propositions in the associated ''differential universe'' <math>\mathrm{d}U^\bullet = [\mathrm{d}u, \mathrm{d}v].\!</math>  These are the propositions that are commonly denoted: <math>{0, ~\mathrm{d}u, ~\mathrm{d}v, ~\mathrm{d}u + \mathrm{d}v},\!</math> in other words:  <math>\texttt{(~)}, ~\mathrm{d}u, ~\mathrm{d}v, ~\texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}.\!</math>
−
in the associated "differential universe" dU% = [du, dv],
 
−
and these are the propositions that are commonly denoted:
 
−
0, du, dv, du + dv, in other words, (), du, dv, (du, dv).
 
−
</pre>
 
  
−
==Note 16==
+
==Notions of Approximation==
  
−
<pre>
+
{| cellpadding="2" cellspacing="2" width="100%"
−
| for equalities are so weighed
+
| width="60%" | &nbsp;
−
| that curiosity in neither can
+
| width="40%" |
−
| make choice of either's moiety.
+
for equalities are so weighed<br>
 +
that curiosity in neither can<br>
 +
make choice of either's moiety.
 +
|-
 +
| height="50px" | &nbsp;
 +
| valign="top"  | &mdash; ''King Lear'', Sc.1.5&ndash;7 (Quarto)
 +
|-
 +
| &nbsp;
 
|
 
|
−
| King Lear, Sc.1.5-7, (Quarto)
+
for qualities are so weighed<br>
 +
that curiosity in neither can<br>
 +
make choice of either's moiety.<br>
 +
|-
 +
| height="50px" | &nbsp;
 +
| valign="top"  | &mdash; ''King Lear'', 1.1.5&ndash;6 (Folio)
  
−
| for qualities are so weighed
+
|}
−
| that curiosity in neither can
 
−
| make choice of either's moiety.
 
−
|
 
−
| King Lear, 1.1.5-6, (Folio)
 
  
−
Justifying a notion of approximation is a little more
+
Justifying a notion of approximation is a little more involved in general, and especially in these discrete logical spaces, than it would be expedient for people in a hurry to tangle with right now.  I will just say that there are ''naive'' or ''obvious'' notions and there are ''sophisticated'' or ''subtle'' notions that we might choose among.  The later would engage us in trying to construct proper logical analogues of Lie derivatives, and so let's save that for when we have become subtle or sophisticated or both.  Against or toward that day, as you wish, let's begin with an option in plain view.
−
involved in general, and especially in these discrete
 
−
logical spaces, than it would be expedient for people
 
−
in a hurry to tangle with right now.  I will just say
 
−
that there are "naive" or "obvious" notions and there
 
−
are "sophisticated" or "subtle" notions that we might
 
−
choose among.  The later would engage us in trying to
 
−
construct proper logical analogues of Lie derivatives,
 
−
and so let's save that for when we have become subtle
 
−
or sophisticated or both.  Against or toward that day,
 
−
as you wish, let's begin with an option in plain view.
 
  
−
Figure 1.4 illustrates one way of ranging over the cells of the
+
Figure&nbsp;1.4 illustrates one way of ranging over the cells of the underlying universe <math>U^\bullet = [u, v]\!</math> and selecting at each cell the linear proposition in <math>\mathrm{d}U^\bullet = [\mathrm{d}u, \mathrm{d}v]\!</math> that best approximates the patch of the difference map <math>{\mathrm{D}f}\!</math> that is located there, yielding the following formula for the differential <math>\mathrm{d}f.\!</math>
−
underlying universe U% = [u, v] and selecting at each cell the
 
−
linear proposition in dU% = [du, dv] that best approximates
 
−
the patch of the difference map Df that is located there,
 
−
yielding the following formula for the differential df.
 
  
−
df  = uv.0 + u(v).du + (u)v.dv + (u)(v).(du, dv)
+
{| align="center" cellpadding="8" style="text-align:center; width:100%"
 +
|
 +
<math>\begin{array}{*{11}{c}}
 +
\mathrm{d}f
 +
& = & \mathrm{d}\texttt{((} u \texttt{)(} v \texttt{))}
 +
& = & uv \cdot 0
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
 +
\end{array}</math>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/`\``````````````````|
+
|                 / \                 |
−
|`````````````````/```\`````````````````|
+
|                 /   \                 |
−
|````````````````/`````\````````````````|
+
|               /     \               |
−
|```````````````o```````o```````````````|
+
|               o       o               |
−
|``````````````/`\`````/`\``````````````|
+
|             / \     / \             |
−
|`````````````/```\```/```\`````````````|
+
|             /   \   /   \             |
−
|````````````/`````\`/`````\````````````|
+
|           /     \ /     \           |
−
|```````````o```````o```````o```````````|
+
|           o       o       o           |
−
|``````````/`\`````/`\`````/`\``````````|
+
|         / \     / \     / \         |
−
|`````````/```\```/```\```/```\`````````|
+
|         /   \   /   \   /   \         |
−
|````````/`````\`/`````\`/`````\````````|
+
|       /     \ /     \ /     \       |
−
|```````o```````o```````o```````o```````|
+
|       o       o       o       o       |
−
|``````/`\`````/%\`````/%\`````/`\``````|
+
|     / \     /%\     /%\     / \     |
−
|`````/```\```/%%%\```/%%%\```/```\`````|
+
|     /   \   /%%%\   /%%%\   /   \     |
−
|````/`````\`/%%%%%\`/%%%%%\`/`````\````|
+
|   /     \ /%%%%%\ /%%%%%\ /     \   |
−
|```o```````o%%%%%%%o%%%%%%%o```````o```|
+
|   o       o%%%%%%%o%%%%%%%o       o   |
−
|```|\`````/%\%%%%%/`\%%%%%/%\`````/|```|
+
|   |\     /%\%%%%%/ \%%%%%/%\     /|   |
−
|```|`\```/%%%\%%%/```\%%%/%%%\```/`|```|
+
|   | \   /%%%\%%%/   \%%%/%%%\   / |   |
−
|```|``\`/%%%%%\%/`````\%/%%%%%\`/``|```|
+
|   | \ /%%%%%\%/     \%/%%%%%\ / |   |
−
|```|```o%%%%%%%o```````o%%%%%%%o```|```|
+
|   |   o%%%%%%%o       o%%%%%%%o   |   |
−
|```|```|\%%%%%/%\`````/%\%%%%%/|```|```|
+
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
−
|```|```|`\%%%/%%%\```/%%%\%%%/`|```|```|
+
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
−
|```|`u`|``\%/%%%%%\`/%%%%%\%/``|`v`|```|
+
|   | u | \%/%%%%%\ /%%%%%\%/ | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/`\%%%%%/````|```````|
+
|       |   \%%%%%/ \%%%%%/   |       |
−
|```````|`````\%%%/```\%%%/`````|```````|
+
|       |     \%%%/   \%%%/     |       |
−
|```````|`du```\%/`````\%/```dv`|```````|
+
|       | du   \%/     \%/   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 1.4.  df = linear approx to Df
 
Figure 1.4.  df = linear approx to Df
 +
</pre>
 +
|}
  
−
Figure 2.4. illustrates one way of ranging over the cells of the
+
Figure&nbsp;2.4 illustrates one way of ranging over the cells of the underlying universe <math>U^\bullet = [u, v]\!</math> and selecting at each cell the linear proposition in <math>\mathrm{d}U^\bullet = [du, dv]\!</math> that best approximates the patch of the difference map <math>\mathrm{D}g\!</math> that is located there, yielding the following formula for the differential <math>\mathrm{d}g.\!</math>
−
underlying universe U% = [u, v] and selecting at each cell the
 
−
linear proposition in dU% = [du, dv] that best approximates
 
−
the patch of the difference map Dg that is located there,
 
−
yielding the following formula for the differential dg.
 
  
−
dg  = uv.(du, dv) + u(v).(du, dv) + (u)v.(du, dv) + (u)(v).(du, dv)
+
{| align="center" cellpadding="8" style="text-align:center; width:100%"
 +
|
 +
<math>\begin{array}{*{11}{c}}
 +
\mathrm{d}g
 +
& = & \mathrm{d}\texttt{((} u \texttt{,} v \texttt{))}
 +
& = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)}
 +
\end{array}</math>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/`\``````````````````|
+
|                 / \                 |
−
|`````````````````/```\`````````````````|
+
|                 /   \                 |
−
|````````````````/`````\````````````````|
+
|               /     \               |
−
|```````````````o```````o```````````````|
+
|               o       o               |
−
|``````````````/%\`````/%\``````````````|
+
|             /%\     /%\             |
−
|`````````````/%%%\```/%%%\`````````````|
+
|             /%%%\   /%%%\             |
−
|````````````/%%%%%\`/%%%%%\````````````|
+
|           /%%%%%\ /%%%%%\           |
−
|```````````o%%%%%%%o%%%%%%%o```````````|
+
|           o%%%%%%%o%%%%%%%o           |
−
|``````````/%\%%%%%/`\%%%%%/%\``````````|
+
|         /%\%%%%%/ \%%%%%/%\         |
−
|`````````/%%%\%%%/```\%%%/%%%\`````````|
+
|         /%%%\%%%/   \%%%/%%%\         |
−
|````````/%%%%%\%/`````\%/%%%%%\````````|
+
|       /%%%%%\%/     \%/%%%%%\       |
−
|```````o%%%%%%%o```````o%%%%%%%o```````|
+
|       o%%%%%%%o       o%%%%%%%o       |
−
|``````/`\%%%%%/`\`````/`\%%%%%/`\``````|
+
|     / \%%%%%/ \     / \%%%%%/ \     |
−
|`````/```\%%%/```\```/```\%%%/```\`````|
+
|     /   \%%%/   \   /   \%%%/   \     |
−
|````/`````\%/`````\`/`````\%/`````\````|
+
|   /     \%/     \ /     \%/     \   |
−
|```o```````o```````o```````o```````o```|
+
|   o       o       o       o       o   |
−
|```|\`````/%\`````/`\`````/%\`````/|```|
+
|   |\     /%\     / \     /%\     /|   |
−
|```|`\```/%%%\```/```\```/%%%\```/`|```|
+
|   | \   /%%%\   /   \   /%%%\   / |   |
−
|```|``\`/%%%%%\`/`````\`/%%%%%\`/``|```|
+
|   | \ /%%%%%\ /     \ /%%%%%\ / |   |
−
|```|```o%%%%%%%o```````o%%%%%%%o```|```|
+
|   |   o%%%%%%%o       o%%%%%%%o   |   |
−
|```|```|\%%%%%/%\`````/%\%%%%%/|```|```|
+
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
−
|```|```|`\%%%/%%%\```/%%%\%%%/`|```|```|
+
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
−
|```|`u`|``\%/%%%%%\`/%%%%%\%/``|`v`|```|
+
|   | u | \%/%%%%%\ /%%%%%\%/ | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/`\%%%%%/````|```````|
+
|       |   \%%%%%/ \%%%%%/   |       |
−
|```````|`````\%%%/```\%%%/`````|```````|
+
|       |     \%%%/   \%%%/     |       |
−
|```````|`du```\%/`````\%/```dv`|```````|
+
|       | du   \%/     \%/   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 2.4.  dg = linear approx to Dg
 
Figure 2.4.  dg = linear approx to Dg
 +
</pre>
 +
|}
  
−
Well, g, that was easy, seeing as how Dg
+
Well, <math>g,\!</math> that was easy, seeing as how <math>\mathrm{D}g\!</math> is already linear at each locus, <math>\mathrm{d}g = \mathrm{D}g.\!</math>
−
is already linear at each locus, dg = Dg.
 
−
</pre>
 
  
−
==Note 17==
+
==Analytic Series==
  
−
<pre>
+
We have been conducting the differential analysis of the logical transformation <math>F : [u, v] \mapsto [u, v]\!</math> defined as <math>F : (u, v) \mapsto ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ ),\!</math> and this means starting with the extended transformation <math>\mathrm{E}F : [u, v, \mathrm{d}u, \mathrm{d}v] \to [u, v, \mathrm{d}u, \mathrm{d}v]\!</math> and breaking it into an analytic series, <math>\mathrm{E}F = F + \mathrm{d}F + \mathrm{d}^2 F + \ldots,\!</math> and so on until there is nothing left to analyze any further.
−
We have been conducting the differential analysis
 
−
of the logical transformation F : [u, v] -> [u, v]
 
−
defined as F : <u, v> ~> <((u)(v)), ((u, v))>, and
 
−
this means starting with the extended transformation
 
−
EF : [u, v, du, dv] -> [u, v, du, dv] and breaking it
 
−
into an analytic series, EF = F + dF + d^2.F + ..., and
 
−
so on until there is nothing left to analyze any further.
 
  
 
As a general rule, one proceeds by way of the following stages:
 
As a general rule, one proceeds by way of the following stages:
  
−
1. EF      = [d^0]F + [r^0]F
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{*{6}{l}}
 +
1. & \mathrm{E}F
 +
& = & \mathrm{d}^0 F
 +
& + & \mathrm{r}^0 F
 +
\\
 +
2. & \mathrm{r}^0 F
 +
& = & \mathrm{d}^1 F
 +
& + & \mathrm{r}^1 F
 +
\\
 +
3. & \mathrm{r}^1 F
 +
& = & \mathrm{d}^2 F
 +
& + & \mathrm{r}^2 F
 +
\\
 +
4. & \ldots
 +
\end{array}</math>
 +
|}
  
−
2.  [r^0]F = [d^1]F + [r^1]F
+
In our analysis of the transformation <math>F,\!</math> we carried out Step&nbsp;1 in the more familiar form <math>\mathrm{E}F = F + \mathrm{D}F\!</math> and we have just reached Step&nbsp;2 in the form <math>\mathrm{D}F = \mathrm{d}F + \mathrm{r}F,\!</math> where <math>\mathrm{r}F\!</math> is the residual term that remains for us to examine next.
  
−
3.  [r^1]F  = [d^2]F + [r^2]F
+
'''Note.''' I'm am trying to give quick overview here, and this forces me to omit many picky details. The picky reader may wish to consult the more detailed presentation of this material at the following locations:
  
−
4.  ...
+
:* [[Differential Logic and Dynamic Systems 2.0|Differential Logic and Dynamic Systems]]
 +
::* [[Differential Logic and Dynamic Systems 2.0#The Secant Operator : E|The Secant Operator]]
 +
::* [[Differential Logic and Dynamic Systems 2.0#Taking Aim at Higher Dimensional Targets|Higher Dimensional Targets]]
  
−
In our analysis of the current transformation F,
+
Let's push on with the analysis of the transformation:
−
we carried out Step 1 in the more familiar form
 
−
EF = F + DF, and we have just reached Step 2 in
 
−
the form DF = dF + rF, where rF is the residual
 
−
term that remains for us to examine next.
 
  
−
NB.  I'm am trying to give quick overview here,
+
{| align="center" cellpadding="8" width="90%"
−
and this forces me to omit many picky details.
+
|
−
The picky reader may wish to consult the more
+
<math>\begin{matrix}
−
detailed presentation of this material in the
+
F & : & (u, v) & \mapsto & (f(u, v), g(u, v))
−
following ur-neighborhoods:
+
& = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~)
 +
\end{matrix}</math>
 +
|}
  
−
Jon Awbrey, "Differential Logic and Dynamic Systems"
+
For ease of comparison and computation, I will collect the Figures that we need for the remainder of the work together on one page.
  
−
DLOG D.  http://stderr.org/pipermail/inquiry/2003-May/thread.html#478
+
===Computation Summary for Logical Disjunction===
−
DLOG D.  http://stderr.org/pipermail/inquiry/2003-June/thread.html#553
 
  
−
Especially:
+
Figure&nbsp;1.1 shows the expansion of <math>f = \texttt{((} u \texttt{)(} v \texttt{))}\!</math> over <math>[u, v]\!</math> to produce the expression:
  
−
DLOG D40.  http://stderr.org/pipermail/inquiry/2003-May/000521.html
+
{| align="center" cellpadding="8" width="90%"
−
DLOG D71.  http://stderr.org/pipermail/inquiry/2003-June/000554.html
+
|
 +
<math>\begin{matrix}
 +
uv & + & u \texttt{(} v \texttt{)} & + & \texttt{(} u \texttt{)} v
 +
\end{matrix}</math>
 +
|}
  
−
Take your pick, Gimli ...
+
Figure&nbsp;1.2 shows the expansion of <math>\mathrm{E}f = \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}\!</math> over <math>[u, v]\!</math> to produce the expression:
−
</pre>
 
  
−
==Note 18==
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{matrix}
 +
uv \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)} & + &
 +
u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} & + &
 +
\texttt{(} u \texttt{)} v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)} & + &
 +
\texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
\end{matrix}</math>
 +
|}
  
−
<pre>
+
In general, <math>\mathrm{E}f\!</math> tells you what you would have to do, from wherever you are in the universe <math>[u, v],\!</math> if you want to end up in a place where <math>f\!</math> is true.  In this case, where the prevailing proposition <math>f\!</math> is <math>\texttt{((} u \texttt{)(} v \texttt{))},\!</math> the indication <math>uv \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)}\!</math> of <math>\mathrm{E}f\!</math> tells you this: If <math>u\!</math> and <math>v\!</math> are both true where you are, then just don't change both <math>u\!</math> and <math>v\!</math> at once, and you will end up in a place where <math>\texttt{((} u \texttt{)(} v \texttt{))}\!</math> is true.
−
Let's push on with the analysis of the transformation:
 
  
−
F : <u, v> ~> <f<u, v>, g<u, v>> = <((u)(v)), ((u, v))>
+
Figure&nbsp;1.3 shows the expansion of <math>\mathrm{D}f</math> over <math>[u, v]\!</math> to produce the expression:
  
−
For ease of comparison and computation, I will collect
+
{| align="center" cellpadding="8" width="90%"
−
the Figures that we need for the remainder of the work
+
|
−
together on one page.
+
<math>\begin{matrix}
 +
uv \cdot \mathrm{d}u ~ \mathrm{d}v & + &
 +
u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + &
 +
\texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + &
 +
\texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))}
 +
\end{matrix}</math>
 +
|}
  
−
Computation Summary for f<u, v> = ((u)(v))
+
In general, <math>{\mathrm{D}f}\!</math> tells you what you would have to do, from wherever you are in the universe <math>[u, v],\!</math> if you want to bring about a change in the value of <math>f,\!</math> that is, if you want to get to a place where the value of <math>f\!</math> is different from what it is where you are.  In the present case, where the reigning proposition <math>f\!</math> is <math>\texttt{((} u \texttt{)(} v \texttt{))},\!</math> the term <math>uv \cdot \mathrm{d}u ~ \mathrm{d}v\!</math> of <math>{\mathrm{D}f}\!</math> tells you this:  If <math>u\!</math> and <math>v\!</math> are both true where you are, then you would have to change both <math>u\!</math> and <math>v\!</math> in order to reach a place where the value of <math>f\!</math> is different from what it is where you are.
  
−
Figure 1.1 expands f = ((u)(v)) over [u, v] to produce
+
Figure&nbsp;1.4 approximates <math>{\mathrm{D}f}\!</math> by the linear form <math>\mathrm{d}f\!</math> that expands over <math>[u, v]\!</math> as follows:
−
the equivalent exclusive disjunction uv + u(v) + (u)v.
 
  
−
Figure 1.2 expands Ef = ((u + du)(v + dv)) over [u, v] to arrive at
+
{| align="center" cellpadding="8" width="90%"
−
Ef = uv (du dv) + u(v) (du (dv)) + (u)v ((du) dv) + (u)(v)((du)(dv)).
+
|
 +
<math>\begin{matrix}
 +
\mathrm{d}f
 +
& = & uv \cdot 0
 +
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u
 +
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
 +
\\[8pt]
 +
& = &&& u \texttt{(} v \texttt{)} \cdot \mathrm{d}u
 +
& + &  \texttt{(} u \texttt{)} v \cdot \mathrm{d}v
 +
& + &  \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
 +
\end{matrix}</math>
 +
|}
  
−
Ef tells you what you would have to do, from where you are in the
+
Figure&nbsp;1.5 shows what remains of the difference map <math>{\mathrm{D}f}\!</math> when the first order linear contribution <math>\mathrm{d}f\!</math> is removed, namely:
−
universe [u, v], if you want to end up in a place where f is true.
 
−
In this case, where the prevailing proposition f is ((u)(v)), the
 
−
indication uv (du dv) of Ef tells you this: If u and v are both
 
−
true where you are, then just don't change both u and v at once,
 
−
and you will end up in a place where ((u)(v)) is true.
 
  
−
Figure 1.3 expands Df over [u, v] to end up with the formula:
+
{| align="center" cellpadding="8" width="90%"
−
Df = uv du dv + u(v) du(dv) + (u)v (du)dv + (u)(v)((du)(dv)).
+
|
−
 
+
<math>\begin{array}{*{9}{l}}
−
Df tells you what you would have to do, from where you are in the
+
\mathrm{r}f
−
universe [u, v], if you want to bring about a change in the value
+
& = & uv \cdot \mathrm{d}u ~ \mathrm{d}v
−
of f, that is, if you want to get to a place where the value of f
+
& + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
−
is different from what it is where you are.  In the present case,
+
& + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v
−
where the reigning proposition f is ((u)(v)), the term uv du dv
+
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v
−
of Df tells you this:  If u and v are both true where you are,
+
\\[8pt]
−
then you would have to change both u and v in order to reach
+
& = & \mathrm{d}u ~ \mathrm{d}v
−
a place where the value of f is different from what it is
+
\end{array}</math>
−
where you are.
+
|}
−
 
 
−
Figure 1.4 approximates Df by the linear form
 
−
df = uv 0 + u(v) du + (u)v dv + (u)(v)(du, dv).
 
−
 
 
−
Figure 1.5 shows what remains of the difference map Df
 
−
when the first order linear contribution df is removed:
 
−
rf = uv du dv + u(v) du dv + (u)v du dv + (u)(v) du dv.
 
−
This form can be written more succinctly as rf = du dv.
 
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/%\``````````````````|
+
|                 /%\                 |
−
|`````````````````/%%%\`````````````````|
+
|                 /%%%\                 |
−
|````````````````/%%%%%\````````````````|
+
|               /%%%%%\               |
−
|```````````````o%%%%%%%o```````````````|
+
|               o%%%%%%%o               |
−
|``````````````/%\%%%%%/%\``````````````|
+
|             /%\%%%%%/%\             |
−
|`````````````/%%%\%%%/%%%\`````````````|
+
|             /%%%\%%%/%%%\             |
−
|````````````/%%%%%\%/%%%%%\````````````|
+
|           /%%%%%\%/%%%%%\           |
−
|```````````o%%%%%%%o%%%%%%%o```````````|
+
|           o%%%%%%%o%%%%%%%o           |
−
|``````````/%\%%%%%/%\%%%%%/%\``````````|
+
|         /%\%%%%%/%\%%%%%/%\         |
−
|`````````/%%%\%%%/%%%\%%%/%%%\`````````|
+
|         /%%%\%%%/%%%\%%%/%%%\         |
−
|````````/%%%%%\%/%%%%%\%/%%%%%\````````|
+
|       /%%%%%\%/%%%%%\%/%%%%%\       |
−
|```````o%%%%%%%o%%%%%%%o%%%%%%%o```````|
+
|       o%%%%%%%o%%%%%%%o%%%%%%%o       |
−
|``````/%\%%%%%/%\%%%%%/%\%%%%%/%\``````|
+
|     /%\%%%%%/%\%%%%%/%\%%%%%/%\     |
−
|`````/%%%\%%%/%%%\%%%/%%%\%%%/%%%\`````|
+
|     /%%%\%%%/%%%\%%%/%%%\%%%/%%%\     |
−
|````/%%%%%\%/%%%%%\%/%%%%%\%/%%%%%\````|
+
|   /%%%%%\%/%%%%%\%/%%%%%\%/%%%%%\   |
−
|```o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o```|
+
|   o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o   |
−
|```|\%%%%%/%\%%%%%/`\%%%%%/%\%%%%%/|```|
+
|   |\%%%%%/%\%%%%%/ \%%%%%/%\%%%%%/|   |
−
|```|`\%%%/%%%\%%%/```\%%%/%%%\%%%/`|```|
+
|   | \%%%/%%%\%%%/   \%%%/%%%\%%%/ |   |
−
|```|``\%/%%%%%\%/`````\%/%%%%%\%/``|```|
+
|   | \%/%%%%%\%/     \%/%%%%%\%/ |   |
−
|```|```o%%%%%%%o```````o%%%%%%%o```|```|
+
|   |   o%%%%%%%o       o%%%%%%%o   |   |
−
|```|```|\%%%%%/`\`````/`\%%%%%/|```|```|
+
|   |   |\%%%%%/ \     / \%%%%%/|   |   |
−
|```|```|`\%%%/```\```/```\%%%/`|```|```|
+
|   |   | \%%%/   \   /   \%%%/ |   |   |
−
|```|`u`|``\%/`````\`/`````\%/``|`v`|```|
+
|   | u | \%/     \ /     \%/ | v |   |
−
|```o---+---o```````o```````o---+---o```|
+
|   o---+---o       o       o---+---o   |
−
|```````|````\`````/`\`````/````|```````|
+
|       |   \     / \     /   |       |
−
|```````|`````\```/```\```/`````|```````|
+
|       |     \   /   \   /     |       |
−
|```````|`du```\`/`````\`/```dv`|```````|
+
|       | du   \ /     \ /   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 1.1.  f = ((u)(v))
 
Figure 1.1.  f = ((u)(v))
 +
</pre>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/%\``````````````````|
+
|                 /%\                 |
−
|`````````````````/%%%\`````````````````|
+
|                 /%%%\                 |
−
|````````````````/%%%%%\````````````````|
+
|               /%%%%%\               |
−
|```````````````o%%%%%%%o```````````````|
+
|               o%%%%%%%o               |
−
|``````````````/%\%%%%%/%\``````````````|
+
|             /%\%%%%%/%\             |
−
|`````````````/%%%\%%%/%%%\`````````````|
+
|             /%%%\%%%/%%%\             |
−
|````````````/%%%%%\%/%%%%%\````````````|
+
|           /%%%%%\%/%%%%%\           |
−
|```````````o%%%%%%%o%%%%%%%o```````````|
+
|           o%%%%%%%o%%%%%%%o           |
−
|``````````/%\%%%%%/`\%%%%%/%\``````````|
+
|         /%\%%%%%/ \%%%%%/%\         |
−
|`````````/%%%\%%%/```\%%%/%%%\`````````|
+
|         /%%%\%%%/   \%%%/%%%\         |
−
|````````/%%%%%\%/`````\%/%%%%%\````````|
+
|       /%%%%%\%/     \%/%%%%%\       |
−
|```````o%%%%%%%o```````o%%%%%%%o```````|
+
|       o%%%%%%%o       o%%%%%%%o       |
−
|``````/%\%%%%%/%\`````/%\%%%%%/%\``````|
+
|     /%\%%%%%/%\     /%\%%%%%/%\     |
−
|`````/%%%\%%%/%%%\```/%%%\%%%/%%%\`````|
+
|     /%%%\%%%/%%%\   /%%%\%%%/%%%\     |
−
|````/%%%%%\%/%%%%%\`/%%%%%\%/%%%%%\````|
+
|   /%%%%%\%/%%%%%\ /%%%%%\%/%%%%%\   |
−
|```o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o```|
+
|   o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o   |
−
|```|\%%%%%/`\%%%%%/%\%%%%%/`\%%%%%/|```|
+
|   |\%%%%%/ \%%%%%/%\%%%%%/ \%%%%%/|   |
−
|```|`\%%%/```\%%%/%%%\%%%/```\%%%/`|```|
+
|   | \%%%/   \%%%/%%%\%%%/   \%%%/ |   |
−
|```|``\%/`````\%/%%%%%\%/`````\%/``|```|
+
|   | \%/     \%/%%%%%\%/     \%/ |   |
−
|```|```o```````o%%%%%%%o```````o```|```|
+
|   |   o       o%%%%%%%o       o   |   |
−
|```|```|\`````/%\%%%%%/%\`````/|```|```|
+
|   |   |\     /%\%%%%%/%\     /|   |   |
−
|```|```|`\```/%%%\%%%/%%%\```/`|```|```|
+
|   |   | \   /%%%\%%%/%%%\   / |   |   |
−
|```|`u`|``\`/%%%%%\%/%%%%%\`/``|`v`|```|
+
|   | u | \ /%%%%%\%/%%%%%\ / | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/`\%%%%%/````|```````|
+
|       |   \%%%%%/ \%%%%%/   |       |
−
|```````|`````\%%%/```\%%%/`````|```````|
+
|       |     \%%%/   \%%%/     |       |
−
|```````|`du```\%/`````\%/```dv`|```````|
+
|       | du   \%/     \%/   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 1.2.  Ef = ((u + du)(v + dv))
 
Figure 1.2.  Ef = ((u + du)(v + dv))
 +
</pre>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/`\``````````````````|
+
|                 / \                 |
−
|`````````````````/```\`````````````````|
+
|                 /   \                 |
−
|````````````````/`````\````````````````|
+
|               /     \               |
−
|```````````````o```````o```````````````|
+
|               o       o               |
−
|``````````````/`\`````/`\``````````````|
+
|             / \     / \             |
−
|`````````````/```\```/```\`````````````|
+
|             /   \   /   \             |
−
|````````````/`````\`/`````\````````````|
+
|           /     \ /     \           |
−
|```````````o```````o```````o```````````|
+
|           o       o       o           |
−
|``````````/`\`````/%\`````/`\``````````|
+
|         / \     /%\     / \         |
−
|`````````/```\```/%%%\```/```\`````````|
+
|         /   \   /%%%\   /   \         |
−
|````````/`````\`/%%%%%\`/`````\````````|
+
|       /     \ /%%%%%\ /     \       |
−
|```````o```````o%%%%%%%o```````o```````|
+
|       o       o%%%%%%%o       o       |
−
|``````/`\`````/`\%%%%%/`\`````/`\``````|
+
|     / \     / \%%%%%/ \     / \     |
−
|`````/```\```/```\%%%/```\```/```\`````|
+
|     /   \   /   \%%%/   \   /   \     |
−
|````/`````\`/`````\%/`````\`/`````\````|
+
|   /     \ /     \%/     \ /     \   |
−
|```o```````o```````o```````o```````o```|
+
|   o       o       o       o       o   |
−
|```|\`````/%\`````/%\`````/%\`````/|```|
+
|   |\     /%\     /%\     /%\     /|   |
−
|```|`\```/%%%\```/%%%\```/%%%\```/`|```|
+
|   | \   /%%%\   /%%%\   /%%%\   / |   |
−
|```|``\`/%%%%%\`/%%%%%\`/%%%%%\`/``|```|
+
|   | \ /%%%%%\ /%%%%%\ /%%%%%\ / |   |
−
|```|```o%%%%%%%o%%%%%%%o%%%%%%%o```|```|
+
|   |   o%%%%%%%o%%%%%%%o%%%%%%%o   |   |
−
|```|```|\%%%%%/%\%%%%%/%\%%%%%/|```|```|
+
|   |   |\%%%%%/%\%%%%%/%\%%%%%/|   |   |
−
|```|```|`\%%%/%%%\%%%/%%%\%%%/`|```|```|
+
|   |   | \%%%/%%%\%%%/%%%\%%%/ |   |   |
−
|```|`u`|``\%/%%%%%\%/%%%%%\%/``|`v`|```|
+
|   | u | \%/%%%%%\%/%%%%%\%/ | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/`\%%%%%/````|```````|
+
|       |   \%%%%%/ \%%%%%/   |       |
−
|```````|`````\%%%/```\%%%/`````|```````|
+
|       |     \%%%/   \%%%/     |       |
−
|```````|`du```\%/`````\%/```dv`|```````|
+
|       | du   \%/     \%/   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 1.3.  Difference Map Df = f + Ef
 
Figure 1.3.  Difference Map Df = f + Ef
 +
</pre>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/`\``````````````````|
+
|                 / \                 |
−
|`````````````````/```\`````````````````|
+
|                 /   \                 |
−
|````````````````/`````\````````````````|
+
|               /     \               |
−
|```````````````o```````o```````````````|
+
|               o       o               |
−
|``````````````/`\`````/`\``````````````|
+
|             / \     / \             |
−
|`````````````/```\```/```\`````````````|
+
|             /   \   /   \             |
−
|````````````/`````\`/`````\````````````|
+
|           /     \ /     \           |
−
|```````````o```````o```````o```````````|
+
|           o       o       o           |
−
|``````````/`\`````/`\`````/`\``````````|
+
|         / \     / \     / \         |
−
|`````````/```\```/```\```/```\`````````|
+
|         /   \   /   \   /   \         |
−
|````````/`````\`/`````\`/`````\````````|
+
|       /     \ /     \ /     \       |
−
|```````o```````o```````o```````o```````|
+
|       o       o       o       o       |
−
|``````/`\`````/%\`````/%\`````/`\``````|
+
|     / \     /%\     /%\     / \     |
−
|`````/```\```/%%%\```/%%%\```/```\`````|
+
|     /   \   /%%%\   /%%%\   /   \     |
−
|````/`````\`/%%%%%\`/%%%%%\`/`````\````|
+
|   /     \ /%%%%%\ /%%%%%\ /     \   |
−
|```o```````o%%%%%%%o%%%%%%%o```````o```|
+
|   o       o%%%%%%%o%%%%%%%o       o   |
−
|```|\`````/%\%%%%%/`\%%%%%/%\`````/|```|
+
|   |\     /%\%%%%%/ \%%%%%/%\     /|   |
−
|```|`\```/%%%\%%%/```\%%%/%%%\```/`|```|
+
|   | \   /%%%\%%%/   \%%%/%%%\   / |   |
−
|```|``\`/%%%%%\%/`````\%/%%%%%\`/``|```|
+
|   | \ /%%%%%\%/     \%/%%%%%\ / |   |
−
|```|```o%%%%%%%o```````o%%%%%%%o```|```|
+
|   |   o%%%%%%%o       o%%%%%%%o   |   |
−
|```|```|\%%%%%/%\`````/%\%%%%%/|```|```|
+
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
−
|```|```|`\%%%/%%%\```/%%%\%%%/`|```|```|
+
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
−
|```|`u`|``\%/%%%%%\`/%%%%%\%/``|`v`|```|
+
|   | u | \%/%%%%%\ /%%%%%\%/ | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/`\%%%%%/````|```````|
+
|       |   \%%%%%/ \%%%%%/   |       |
−
|```````|`````\%%%/```\%%%/`````|```````|
+
|       |     \%%%/   \%%%/     |       |
−
|```````|`du```\%/`````\%/```dv`|```````|
+
|       | du   \%/     \%/   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 1.4.  Linear Proxy df for Df
 
Figure 1.4.  Linear Proxy df for Df
 +
</pre>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/`\``````````````````|
+
|                 / \                 |
−
|`````````````````/```\`````````````````|
+
|                 /   \                 |
−
|````````````````/`````\````````````````|
+
|               /     \               |
−
|```````````````o```````o```````````````|
+
|               o       o               |
−
|``````````````/`\`````/`\``````````````|
+
|             / \     / \             |
−
|`````````````/```\```/```\`````````````|
+
|             /   \   /   \             |
−
|````````````/`````\`/`````\````````````|
+
|           /     \ /     \           |
−
|```````````o```````o```````o```````````|
+
|           o       o       o           |
−
|``````````/`\`````/%\`````/`\``````````|
+
|         / \     /%\     / \         |
−
|`````````/```\```/%%%\```/```\`````````|
+
|         /   \   /%%%\   /   \         |
−
|````````/`````\`/%%%%%\`/`````\````````|
+
|       /     \ /%%%%%\ /     \       |
−
|```````o```````o%%%%%%%o```````o```````|
+
|       o       o%%%%%%%o       o       |
−
|``````/`\`````/%\%%%%%/%\`````/`\``````|
+
|     / \     /%\%%%%%/%\     / \     |
−
|`````/```\```/%%%\%%%/%%%\```/```\`````|
+
|     /   \   /%%%\%%%/%%%\   /   \     |
−
|````/`````\`/%%%%%\%/%%%%%\`/`````\````|
+
|   /     \ /%%%%%\%/%%%%%\ /     \   |
−
|```o```````o%%%%%%%o%%%%%%%o```````o```|
+
|   o       o%%%%%%%o%%%%%%%o       o   |
−
|```|\`````/`\%%%%%/%\%%%%%/`\`````/|```|
+
|   |\     / \%%%%%/%\%%%%%/ \     /|   |
−
|```|`\```/```\%%%/%%%\%%%/```\```/`|```|
+
|   | \   /   \%%%/%%%\%%%/   \   / |   |
−
|```|``\`/`````\%/%%%%%\%/`````\`/``|```|
+
|   | \ /     \%/%%%%%\%/     \ / |   |
−
|```|```o```````o%%%%%%%o```````o```|```|
+
|   |   o       o%%%%%%%o       o   |   |
−
|```|```|\`````/`\%%%%%/`\`````/|```|```|
+
|   |   |\     / \%%%%%/ \     /|   |   |
−
|```|```|`\```/```\%%%/```\```/`|```|```|
+
|   |   | \   /   \%%%/   \   / |   |   |
−
|```|`u`|``\`/`````\%/`````\`/``|`v`|```|
+
|   | u | \ /     \%/     \ / | v |   |
−
|```o---+---o```````o```````o---+---o```|
+
|   o---+---o       o       o---+---o   |
−
|```````|````\`````/`\`````/````|```````|
+
|       |   \     / \     /   |       |
−
|```````|`````\```/```\```/`````|```````|
+
|       |     \   /   \   /     |       |
−
|```````|`du```\`/`````\`/```dv`|```````|
+
|       | du   \ /     \ /   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 1.5.  Remainder rf = Df + df
 
Figure 1.5.  Remainder rf = Df + df
 +
</pre>
 +
|}
  
−
Computation Summary for g<u, v> = ((u, v))
+
===Computation Summary for Logical Equality===
  
−
Exercise for the Reader.
+
Figure&nbsp;2.1 shows the expansion of <math>g = \texttt{((} u \texttt{,~} v \texttt{))}\!</math> over <math>[u, v]\!</math> to produce the expression:
−
</pre>
+
 
 +
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{matrix}
 +
uv & + & \texttt{(} u \texttt{)(} v \texttt{)}
 +
\end{matrix}</math>
 +
|}
  
−
==Note 19==
+
Figure&nbsp;2.2 shows the expansion of <math>\mathrm{E}g = \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))}\!</math> over <math>[u, v]\!</math> to produce the expression:
  
−
<pre>
+
{| align="center" cellpadding="8"  width="90%"
−
I'd never rob readers of exercise ...
+
|
−
but for my ain sense of an ending ---
+
<math>\begin{matrix}
 +
uv \cdot \texttt{((} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{))} & + &
 +
u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} & + &
 +
\texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} & + &
 +
\texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{))}
 +
\end{matrix}</math>
 +
|}
  
−
Computation Summary for g<u, v> = ((u, v))
+
In general, <math>\mathrm{E}g\!</math> tells you what you would have to do, from wherever you are in the universe <math>[u, v],\!</math> if you want to end up in a place where <math>g\!</math> is true.  In this case, where the prevailing proposition <math>g\!</math> is <math>\texttt{((} u \texttt{,~} v \texttt{))},\!</math> the component <math>uv \cdot \texttt{((} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{))}\!</math> of <math>\mathrm{E}g\!</math> tells you this:  If <math>u\!</math> and <math>v\!</math> are both true where you are, then change either both or neither of <math>u\!</math> and <math>v\!</math> at the same time, and you will attain a place where <math>\texttt{((} u \texttt{,~} v \texttt{))}\!</math> is true.
  
−
Figure 2.1 expands g = ((u, v)) over [u, v] to get
+
Figure&nbsp;2.3 shows the expansion of <math>\mathrm{D}g\!</math> over <math>[u, v]\!</math> to produce the expression:
−
the equivalent exclusive disjunction u v + (u)(v).
 
  
−
Figure 2.2 expands Eg = ((u + du, v + dv)) over [u, v] to arrive at
+
{| align="center" cellpadding="8"  width="90%"
−
Eg = uv((du, dv)) + u(v)(du, dv) + (u)v (du, dv) + (u)(v)((du, dv)).
+
|
 +
<math>\begin{matrix}
 +
uv \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} & + &
 +
u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} & + &
 +
\texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} & + &
 +
\texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
 +
\end{matrix}</math>
 +
|}
  
−
Eg tells you what you would have to do, from where you are in the
+
In general, <math>\mathrm{D}g\!</math> tells you what you would have to do, from wherever you are in the universe <math>[u, v],\!</math> if you want to bring about a change in the value of <math>g,\!</math> that is, if you want to get to a place where the value of <math>g\!</math> is different from what it is where you are. In the present case, where the ruling proposition <math>g\!</math> is <math>\texttt{((} u \texttt{,~} v \texttt{))},\!</math> the term <math>uv \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}\!</math> of <math>\mathrm{D}g\!</math> tells you this:  If <math>u\!</math> and <math>v\!</math> are both true where you are, then you would have to change one or the other but not both <math>u\!</math> and <math>v\!</math> in order to reach a place where the value of <math>g\!</math> is different from what it is where you are.
−
universe [u, v], if you want to end up in a place where g is true.
 
−
In this case, where the prevailing proposition g is ((u, v)), the
 
−
component uv((du, dv)) of Eg tells you this:  If u and v are both
 
−
true where you are, then change either both or neither u and v at
 
−
the same time, and you will attain a place where ((u, v)) is true.
 
  
−
Figure 2.3 expands Dg over [u, v] to obtain the following formula:
+
Figure&nbsp;2.4 approximates <math>\mathrm{D}g\!</math> by the linear form <math>{\mathrm{d}g}\!</math> that expands over <math>[u, v]\!</math> as follows:
−
Dg = uv (du, dv) + u(v)(du, dv) + (u)v (du, dv) + (u)(v) (du, dv).
 
  
−
Dg tells you what you would have to do, from where you are in the
+
{| align="center" cellpadding="8" width="90%"
−
universe [u, v], if you want to bring about a change in the value
+
|
−
of g, that is, if you want to get to a place where the value of g
+
<math>\begin{array}{*{9}{l}}
−
is different from what it is where you are.  In the present case,
+
\mathrm{d}g
−
where the ruling proposition g is ((u, v)), the term uv (du, dv)
+
& = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
−
of Dg tells you this:  If u and v are both true where you are,
+
& + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
−
then you would have to change one or the other but not both
+
& + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
−
u and v in order to reach a place where the value of g is
+
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
−
different from what it is where you are.
+
\\[8pt]
 +
& = & \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}
 +
\end{array}</math>
 +
|}
  
−
Figure 2.4 approximates Dg in the proxy of the linear proposition
+
Figure&nbsp;2.5 shows what remains of the difference map <math>\mathrm{D}g\!</math> when the first order linear contribution <math>{\mathrm{d}g}\!</math> is removed, namely:
−
dg = uv (du, dv) + u(v)(du, dv) + (u)v (du, dv) + (u)(v) (du, dv).
 
−
Noting the caste of the constant factor (du, dv) distributed over
 
−
the expansion of a tautology, dg may be digested as dg = (du, dv).
 
  
−
Figure 2.5 shows what remains of the difference map Dg
+
{| align="center" cellpadding="8" width="90%"
−
when the first order linear contribution dg is removed,
+
|
−
and this is nothing but nothing at all, leaving rg = 0.
+
<math>\begin{array}{*{9}{l}}
 +
\mathrm{r}g
 +
& = & uv \cdot 0
 +
& + & u \texttt{(} v \texttt{)} \cdot 0
 +
& + & \texttt{(} u \texttt{)} v \cdot 0
 +
& + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0
 +
\\[8pt]
 +
& = & 0
 +
\end{array}</math>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/%\``````````````````|
+
|                 /%\                 |
−
|`````````````````/%%%\`````````````````|
+
|                 /%%%\                 |
−
|````````````````/%%%%%\````````````````|
+
|               /%%%%%\               |
−
|```````````````o%%%%%%%o```````````````|
+
|               o%%%%%%%o               |
−
|``````````````/%\%%%%%/%\``````````````|
+
|             /%\%%%%%/%\             |
−
|`````````````/%%%\%%%/%%%\`````````````|
+
|             /%%%\%%%/%%%\             |
−
|````````````/%%%%%\%/%%%%%\````````````|
+
|           /%%%%%\%/%%%%%\           |
−
|```````````o%%%%%%%o%%%%%%%o```````````|
+
|           o%%%%%%%o%%%%%%%o           |
−
|``````````/`\%%%%%/%\%%%%%/`\``````````|
+
|         / \%%%%%/%\%%%%%/ \         |
−
|`````````/```\%%%/%%%\%%%/```\`````````|
+
|         /   \%%%/%%%\%%%/   \         |
−
|````````/`````\%/%%%%%\%/`````\````````|
+
|       /     \%/%%%%%\%/     \       |
−
|```````o```````o%%%%%%%o```````o```````|
+
|       o       o%%%%%%%o       o       |
−
|``````/`\`````/`\%%%%%/`\`````/`\``````|
+
|     / \     / \%%%%%/ \     / \     |
−
|`````/```\```/```\%%%/```\```/```\`````|
+
|     /   \   /   \%%%/   \   /   \     |
−
|````/`````\`/`````\%/`````\`/`````\````|
+
|   /     \ /     \%/     \ /     \   |
−
|```o```````o```````o```````o```````o```|
+
|   o       o       o       o       o   |
−
|```|\`````/`\`````/%\`````/`\`````/|```|
+
|   |\     / \     /%\     / \     /|   |
−
|```|`\```/```\```/%%%\```/```\```/`|```|
+
|   | \   /   \   /%%%\   /   \   / |   |
−
|```|``\`/`````\`/%%%%%\`/`````\`/``|```|
+
|   | \ /     \ /%%%%%\ /     \ / |   |
−
|```|```o```````o%%%%%%%o```````o```|```|
+
|   |   o       o%%%%%%%o       o   |   |
−
|```|```|\`````/%\%%%%%/%\`````/|```|```|
+
|   |   |\     /%\%%%%%/%\     /|   |   |
−
|```|```|`\```/%%%\%%%/%%%\```/`|```|```|
+
|   |   | \   /%%%\%%%/%%%\   / |   |   |
−
|```|`u`|``\`/%%%%%\%/%%%%%\`/``|`v`|```|
+
|   | u | \ /%%%%%\%/%%%%%\ / | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/%\%%%%%/````|```````|
+
|       |   \%%%%%/%\%%%%%/   |       |
−
|```````|`````\%%%/%%%\%%%/`````|```````|
+
|       |     \%%%/%%%\%%%/     |       |
−
|```````|`du```\%/%%%%%\%/```dv`|```````|
+
|       | du   \%/%%%%%\%/   dv |       |
−
|```````o-------o%%%%%%%o-------o```````|
+
|       o-------o%%%%%%%o-------o       |
−
|````````````````\%%%%%/````````````````|
+
|               \%%%%%/               |
−
|`````````````````\%%%/`````````````````|
+
|                 \%%%/                 |
−
|``````````````````\%/``````````````````|
+
|                 \%/                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 2.1.  g = ((u, v))
 
Figure 2.1.  g = ((u, v))
 +
</pre>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/%\``````````````````|
+
|                 /%\                 |
−
|`````````````````/%%%\`````````````````|
+
|                 /%%%\                 |
−
|````````````````/%%%%%\````````````````|
+
|               /%%%%%\               |
−
|```````````````o%%%%%%%o```````````````|
+
|               o%%%%%%%o               |
−
|``````````````/`\%%%%%/`\``````````````|
+
|             / \%%%%%/ \             |
−
|`````````````/```\%%%/```\`````````````|
+
|             /   \%%%/   \             |
−
|````````````/`````\%/`````\````````````|
+
|           /     \%/     \           |
−
|```````````o```````o```````o```````````|
+
|           o       o       o           |
−
|``````````/%\`````/%\`````/%\``````````|
+
|         /%\     /%\     /%\         |
−
|`````````/%%%\```/%%%\```/%%%\`````````|
+
|         /%%%\   /%%%\   /%%%\         |
−
|````````/%%%%%\`/%%%%%\`/%%%%%\````````|
+
|       /%%%%%\ /%%%%%\ /%%%%%\       |
−
|```````o%%%%%%%o%%%%%%%o%%%%%%%o```````|
+
|       o%%%%%%%o%%%%%%%o%%%%%%%o       |
−
|``````/`\%%%%%/`\%%%%%/`\%%%%%/`\``````|
+
|     / \%%%%%/ \%%%%%/ \%%%%%/ \     |
−
|`````/```\%%%/```\%%%/```\%%%/```\`````|
+
|     /   \%%%/   \%%%/   \%%%/   \     |
−
|````/`````\%/`````\%/`````\%/`````\````|
+
|   /     \%/     \%/     \%/     \   |
−
|```o```````o```````o```````o```````o```|
+
|   o       o       o       o       o   |
−
|```|\`````/%\`````/%\`````/%\`````/|```|
+
|   |\     /%\     /%\     /%\     /|   |
−
|```|`\```/%%%\```/%%%\```/%%%\```/`|```|
+
|   | \   /%%%\   /%%%\   /%%%\   / |   |
−
|```|``\`/%%%%%\`/%%%%%\`/%%%%%\`/``|```|
+
|   | \ /%%%%%\ /%%%%%\ /%%%%%\ / |   |
−
|```|```o%%%%%%%o%%%%%%%o%%%%%%%o```|```|
+
|   |   o%%%%%%%o%%%%%%%o%%%%%%%o   |   |
−
|```|```|\%%%%%/`\%%%%%/`\%%%%%/|```|```|
+
|   |   |\%%%%%/ \%%%%%/ \%%%%%/|   |   |
−
|```|```|`\%%%/```\%%%/```\%%%/`|```|```|
+
|   |   | \%%%/   \%%%/   \%%%/ |   |   |
−
|```|`u`|``\%/`````\%/`````\%/``|`v`|```|
+
|   | u | \%/     \%/     \%/ | v |   |
−
|```o---+---o```````o```````o---+---o```|
+
|   o---+---o       o       o---+---o   |
−
|```````|````\`````/%\`````/````|```````|
+
|       |   \     /%\     /   |       |
−
|```````|`````\```/%%%\```/`````|```````|
+
|       |     \   /%%%\   /     |       |
−
|```````|`du```\`/%%%%%\`/```dv`|```````|
+
|       | du   \ /%%%%%\ /   dv |       |
−
|```````o-------o%%%%%%%o-------o```````|
+
|       o-------o%%%%%%%o-------o       |
−
|````````````````\%%%%%/````````````````|
+
|               \%%%%%/               |
−
|`````````````````\%%%/`````````````````|
+
|                 \%%%/                 |
−
|``````````````````\%/``````````````````|
+
|                 \%/                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 2.2.  Eg = ((u + du, v + dv))
 
Figure 2.2.  Eg = ((u + du, v + dv))
 +
</pre>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/`\``````````````````|
+
|                 / \                 |
−
|`````````````````/```\`````````````````|
+
|                 /   \                 |
−
|````````````````/`````\````````````````|
+
|               /     \               |
−
|```````````````o```````o```````````````|
+
|               o       o               |
−
|``````````````/%\`````/%\``````````````|
+
|             /%\     /%\             |
−
|`````````````/%%%\```/%%%\`````````````|
+
|             /%%%\   /%%%\             |
−
|````````````/%%%%%\`/%%%%%\````````````|
+
|           /%%%%%\ /%%%%%\           |
−
|```````````o%%%%%%%o%%%%%%%o```````````|
+
|           o%%%%%%%o%%%%%%%o           |
−
|``````````/%\%%%%%/`\%%%%%/%\``````````|
+
|         /%\%%%%%/ \%%%%%/%\         |
−
|`````````/%%%\%%%/```\%%%/%%%\`````````|
+
|         /%%%\%%%/   \%%%/%%%\         |
−
|````````/%%%%%\%/`````\%/%%%%%\````````|
+
|       /%%%%%\%/     \%/%%%%%\       |
−
|```````o%%%%%%%o```````o%%%%%%%o```````|
+
|       o%%%%%%%o       o%%%%%%%o       |
−
|``````/`\%%%%%/`\`````/`\%%%%%/`\``````|
+
|     / \%%%%%/ \     / \%%%%%/ \     |
−
|`````/```\%%%/```\```/```\%%%/```\`````|
+
|     /   \%%%/   \   /   \%%%/   \     |
−
|````/`````\%/`````\`/`````\%/`````\````|
+
|   /     \%/     \ /     \%/     \   |
−
|```o```````o```````o```````o```````o```|
+
|   o       o       o       o       o   |
−
|```|\`````/%\`````/`\`````/%\`````/|```|
+
|   |\     /%\     / \     /%\     /|   |
−
|```|`\```/%%%\```/```\```/%%%\```/`|```|
+
|   | \   /%%%\   /   \   /%%%\   / |   |
−
|```|``\`/%%%%%\`/`````\`/%%%%%\`/``|```|
+
|   | \ /%%%%%\ /     \ /%%%%%\ / |   |
−
|```|```o%%%%%%%o```````o%%%%%%%o```|```|
+
|   |   o%%%%%%%o       o%%%%%%%o   |   |
−
|```|```|\%%%%%/%\`````/%\%%%%%/|```|```|
+
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
−
|```|```|`\%%%/%%%\```/%%%\%%%/`|```|```|
+
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
−
|```|`u`|``\%/%%%%%\`/%%%%%\%/``|`v`|```|
+
|   | u | \%/%%%%%\ /%%%%%\%/ | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/`\%%%%%/````|```````|
+
|       |   \%%%%%/ \%%%%%/   |       |
−
|```````|`````\%%%/```\%%%/`````|```````|
+
|       |     \%%%/   \%%%/     |       |
−
|```````|`du```\%/`````\%/```dv`|```````|
+
|       | du   \%/     \%/   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 2.3.  Difference Map Dg = g + Eg
 
Figure 2.3.  Difference Map Dg = g + Eg
 +
</pre>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/`\``````````````````|
+
|                 / \                 |
−
|`````````````````/```\`````````````````|
+
|                 /   \                 |
−
|````````````````/`````\````````````````|
+
|               /     \               |
−
|```````````````o```````o```````````````|
+
|               o       o               |
−
|``````````````/%\`````/%\``````````````|
+
|             /%\     /%\             |
−
|`````````````/%%%\```/%%%\`````````````|
+
|             /%%%\   /%%%\             |
−
|````````````/%%%%%\`/%%%%%\````````````|
+
|           /%%%%%\ /%%%%%\           |
−
|```````````o%%%%%%%o%%%%%%%o```````````|
+
|           o%%%%%%%o%%%%%%%o           |
−
|``````````/%\%%%%%/`\%%%%%/%\``````````|
+
|         /%\%%%%%/ \%%%%%/%\         |
−
|`````````/%%%\%%%/```\%%%/%%%\`````````|
+
|         /%%%\%%%/   \%%%/%%%\         |
−
|````````/%%%%%\%/`````\%/%%%%%\````````|
+
|       /%%%%%\%/     \%/%%%%%\       |
−
|```````o%%%%%%%o```````o%%%%%%%o```````|
+
|       o%%%%%%%o       o%%%%%%%o       |
−
|``````/`\%%%%%/`\`````/`\%%%%%/`\``````|
+
|     / \%%%%%/ \     / \%%%%%/ \     |
−
|`````/```\%%%/```\```/```\%%%/```\`````|
+
|     /   \%%%/   \   /   \%%%/   \     |
−
|````/`````\%/`````\`/`````\%/`````\````|
+
|   /     \%/     \ /     \%/     \   |
−
|```o```````o```````o```````o```````o```|
+
|   o       o       o       o       o   |
−
|```|\`````/%\`````/`\`````/%\`````/|```|
+
|   |\     /%\     / \     /%\     /|   |
−
|```|`\```/%%%\```/```\```/%%%\```/`|```|
+
|   | \   /%%%\   /   \   /%%%\   / |   |
−
|```|``\`/%%%%%\`/`````\`/%%%%%\`/``|```|
+
|   | \ /%%%%%\ /     \ /%%%%%\ / |   |
−
|```|```o%%%%%%%o```````o%%%%%%%o```|```|
+
|   |   o%%%%%%%o       o%%%%%%%o   |   |
−
|```|```|\%%%%%/%\`````/%\%%%%%/|```|```|
+
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
−
|```|```|`\%%%/%%%\```/%%%\%%%/`|```|```|
+
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
−
|```|`u`|``\%/%%%%%\`/%%%%%\%/``|`v`|```|
+
|   | u | \%/%%%%%\ /%%%%%\%/ | v |   |
−
|```o---+---o%%%%%%%o%%%%%%%o---+---o```|
+
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
−
|```````|````\%%%%%/`\%%%%%/````|```````|
+
|       |   \%%%%%/ \%%%%%/   |       |
−
|```````|`````\%%%/```\%%%/`````|```````|
+
|       |     \%%%/   \%%%/     |       |
−
|```````|`du```\%/`````\%/```dv`|```````|
+
|       | du   \%/     \%/   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 2.4.  Linear Proxy dg for Dg
 
Figure 2.4.  Linear Proxy dg for Dg
 +
</pre>
 +
|}
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
|```````````````````````````````````````|
+
|                                       |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|``````````````````/`\``````````````````|
+
|                 / \                 |
−
|`````````````````/```\`````````````````|
+
|                 /   \                 |
−
|````````````````/`````\````````````````|
+
|               /     \               |
−
|```````````````o```````o```````````````|
+
|               o       o               |
−
|``````````````/`\`````/`\``````````````|
+
|             / \     / \             |
−
|`````````````/```\```/```\`````````````|
+
|             /   \   /   \             |
−
|````````````/`````\`/`````\````````````|
+
|           /     \ /     \           |
−
|```````````o```````o```````o```````````|
+
|           o       o       o           |
−
|``````````/`\`````/`\`````/`\``````````|
+
|         / \     / \     / \         |
−
|`````````/```\```/```\```/```\`````````|
+
|         /   \   /   \   /   \         |
−
|````````/`````\`/`````\`/`````\````````|
+
|       /     \ /     \ /     \       |
−
|```````o```````o```````o```````o```````|
+
|       o       o       o       o       |
−
|``````/`\`````/`\`````/`\`````/`\``````|
+
|     / \     / \     / \     / \     |
−
|`````/```\```/```\```/```\```/```\`````|
+
|     /   \   /   \   /   \   /   \     |
−
|````/`````\`/`````\`/`````\`/`````\````|
+
|   /     \ /     \ /     \ /     \   |
−
|```o```````o```````o```````o```````o```|
+
|   o       o       o       o       o   |
−
|```|\`````/`\`````/`\`````/`\`````/|```|
+
|   |\     / \     / \     / \     /|   |
−
|```|`\```/```\```/```\```/```\```/`|```|
+
|   | \   /   \   /   \   /   \   / |   |
−
|```|``\`/`````\`/`````\`/`````\`/``|```|
+
|   | \ /     \ /     \ /     \ / |   |
−
|```|```o```````o```````o```````o```|```|
+
|   |   o       o       o       o   |   |
−
|```|```|\`````/`\`````/`\`````/|```|```|
+
|   |   |\     / \     / \     /|   |   |
−
|```|```|`\```/```\```/```\```/`|```|```|
+
|   |   | \   /   \   /   \   / |   |   |
−
|```|`u`|``\`/`````\`/`````\`/``|`v`|```|
+
|   | u | \ /     \ /     \ / | v |   |
−
|```o---+---o```````o```````o---+---o```|
+
|   o---+---o       o       o---+---o   |
−
|```````|````\`````/`\`````/````|```````|
+
|       |   \     / \     /   |       |
−
|```````|`````\```/```\```/`````|```````|
+
|       |     \   /   \   /     |       |
−
|```````|`du```\`/`````\`/```dv`|```````|
+
|       | du   \ /     \ /   dv |       |
−
|```````o-------o```````o-------o```````|
+
|       o-------o       o-------o       |
−
|````````````````\`````/````````````````|
+
|               \     /               |
−
|`````````````````\```/`````````````````|
+
|                 \   /                 |
−
|``````````````````\`/``````````````````|
+
|                 \ /                 |
−
|```````````````````o```````````````````|
+
|                   o                   |
−
|```````````````````````````````````````|
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 
Figure 2.5.  Remainder rg = Dg + dg
 
Figure 2.5.  Remainder rg = Dg + dg
 +
</pre>
 +
|}
 +
 +
<br>
  
 +
<pre>
 
| Have I carved enough, my lord --
 
| Have I carved enough, my lord --
 
| Child, you are a bone.
 
| Child, you are a bone.
Line 1,611: Line 1,918:
 
</pre>
 
</pre>
  
−
==Note 20==
+
==Visualization==
  
−
<pre>
+
In my work on [[Differential Logic and Dynamic Systems 2.0|Differential Logic and Dynamic Systems]], I found it useful to develop several different ways of visualizing logical transformations, indeed, I devised four distinct styles of picture for the job.  Thus far in our work on the mapping <math>F : [u, v] \to [u, v],\!</math> we've been making use of what I call the ''areal view'' of the extended universe of discourse, <math>[u, v, \mathrm{d}u, \mathrm{d}v],\!</math> but as the number of dimensions climbs beyond four, it's time to bid this genre adieu and look for a style that can scale a little better.  At any rate, before we proceed any further, let's first assemble the information that we have gathered about <math>F\!</math> from several different angles, and see if it can be fitted into a coherent picture of the transformation <math>F : (u, v) \mapsto ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ ).\!</math>
−
In my work on "Differential Logic and Dynamic Systems",
 
−
I found it useful to develop several different ways of
 
−
visualizing logical transformations, indeed, I devised
 
−
four distinct styles of picture for the job.  Thus far
 
−
in our work on the mapping F : [u, v] -> [u, v], we've
 
−
been making use of what I call the "areal view" of the
 
−
extended universe of discourse, [u, v, du, dv], but as
 
−
the number of dimensions climbs beyond four, it's time
 
−
to bid this genre adieu, and look for a style that can
 
−
scale a little better.  At any rate, before we proceed
 
−
any further, let's first assemble the information that
 
−
we have gathered about F from several different angles,
 
−
and see if it can be fitted into a coherent picture of
 
−
the transformation F : <u, v> ~> <((u)(v)), ((u, v))>.
 
  
−
In our first crack at the transformation F, we simply
+
In our first crack at the transformation <math>F,\!</math> we simply plotted the state transitions and applied the utterly stock technique of calculating the finite differences.
−
plotted the state transitions and applied the utterly
 
−
stock technique of calculating the finite differences.
 
  
−
Orbit 1.  u v
+
{| align="center" cellpadding="8" style="text-align:center"
−
o-----o-----o
+
| <math>\text{Orbit 1}\!</math>
−
| ` ` | d d |
+
|-
−
| u v | u v |
+
|
−
o=====o=====o
+
<math>\begin{array}{c|cc|cc|}
−
| 1 1 | 0 0 |
+
t & u & v & \mathrm{d}u & \mathrm{d}v \\[8pt]
−
| " " | " " |
+
0 & 1 & 1 & 0 & 0 \\
−
o-----o-----o
+
1 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel
 +
\end{array}</math>
 +
|}
  
−
A quick inspection of the first Table suggests a rule
+
A quick inspection of the first Table suggests a rule to cover the case when <math>u = v = 1,\!</math> namely, <math>\mathrm{d}u  = \mathrm{d}v = 0.\!</math>  To put it another way, the Table characterizes Orbit&nbsp;1 by means of the data:  <math>(u, v, \mathrm{d}u, \mathrm{d}v) = (1, 1, 0, 0).\!</math> Another way to convey the same information is by means of the extended proposition:  <math>u v \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}.\!</math>
−
to cover the case when u = v = 1, namely, du = dv = 0.
 
−
To put it another way, the Table characterizes Orbit 1
 
−
by means of the data:  <u, v, du, dv>  = <1, 1, 0, 0>.
 
−
Last but not least, yet another way to convey the same
 
−
information is by means of the (first order) extended
 
−
proposition:  u v (du)(dv).
 
  
−
Orbit 2.  (u v)
+
{| align="center" cellpadding="8" style="text-align:center"
−
o-----o-----o-----o
+
| <math>\text{Orbit 2}\!</math>
−
| ` ` | ` ` | d d |
+
|-
−
| ` ` | d d | 2 2 |
+
|
−
| u v | u v | u v |
+
<math>\begin{array}{c|cc|cc|cc|}
−
o=====o=====o=====o
+
t & u & v & \mathrm{d}u & \mathrm{d}v & \mathrm{d}^2 u & \mathrm{d}^2 v \\[8pt]
−
| 0 0 | 0 1 | 1 0 |
+
0 & 0 & 0 & 0 & 1 & 1 & 0 \\
−
| 0 1 | 1 1 | 1 1 |
+
1 & 0 & 1 & 1 & 1 & 1 & 1 \\
−
| 1 0 | 0 0 | 0 0 |
+
2 & 1 & 0 & 0 & 0 & 0 & 0 \\
−
| " " | " " | " " |
+
3 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel
−
o-----o-----o-----o
+
\end{array}</math>
 +
|}
  
−
A more fine combing of the second Table brings to mind
+
A more fine combing of the second Table brings to mind a rule that partly covers the remaining cases, that is, <math>\mathrm{d}u = v, ~ \mathrm{d}v = \texttt{(} u \texttt{)}.\!</math>  This much information about Orbit&nbsp;2 is also encapsulated by the extended proposition <math>\texttt{(} uv \texttt{)((} \mathrm{d}u \texttt{,} v \texttt{))(} \mathrm{d}v, u \texttt{)},\!</math> which says that <math>u\!</math> and <math>v\!</math> are not both true at the same time, while <math>\mathrm{d}u\!</math> is equal in value to <math>v\!</math> and <math>\mathrm{d}v\!</math> is opposite in value to <math>u.\!</math>
−
a rule that partly covers the remaining cases, that is,
+
 
−
du = v, dv = (u). To vary the formulation, this Table
+
==Turing Machine Example==
−
characterizes Orbit 2 by means of the following vector
 
−
equation:  <du, dv> = <v, (u)>. This much information
 
−
about Orbit 2 is also encapsulated by the (first order)
 
−
extended proposition, (uv)((du, v))(dv, u), which says
 
−
that u and v are not both true at the same time, while
 
−
du is equal in value to v, and dv is the opposite of u.
 
−
</pre>
 
  
−
==Note 21==
+
<font size="3">&#9758;</font> See [[Theme One Program]] for documentation of the cactus graph syntax and the propositional modeling program used below.
  
−
<pre>
+
By way of providing a simple illustration of Cook's Theorem, namely, that &ldquo;Propositional Satisfiability is NP-Complete&rdquo;, I will describe one way to translate finite approximations of turing machines into propositional expressions, using the cactus language syntax for propositional calculus that I will describe in more detail as we proceed.
−
By way of providing a simple illustration of Cook's Theorem,
 
−
namely, that "Propositional Satisfiability is NP-Complete",
 
−
I will describe one way to translate finite approximations
 
−
of turing machines into propositional expressions, using
 
−
the cactus language syntax for propositional calculus
 
−
that I will describe in more detail as we proceed.
 
  
−
Notation:
+
:; <math>\mathrm{Stilt}(k) =\!</math>
 +
:: '''Space and time limited turing machine''',
 +
:: with <math>k\!</math> units of space and <math>k\!</math> units of time.
  
−
  Stilt(k) =
+
:; <math>\mathrm{Stunt}(k) =\!</math>
−
  space and time limited turing machine,
+
:: '''Space and time limited turing machine''',
−
  with k units of space and k units of time.
+
:: for computing the parity of a bit string, with number of tape cells of input equal to <math>k.\!</math>
  
−
  Stunt(k) =
+
I will follow the pattern of discussion in Herbert Wilf (1986), ''Algorithms and Complexity'', pp. 188&ndash;201, but translate his logical formalism into cactus language, which is more efficient in regard to the number of propositional clauses that are required.
−
  space and time limited turing machine,
 
−
  for computing the parity of a bit string,
 
−
  with number of tape cells of input equal to k.
 
  
−
I will follow the pattern of discussion in the book
+
A turing machine for computing the parity of a bit string is described by means of the following Figure and Table.
−
by Herbert Wilf, 'Algorithms and Complexity' (1986),
 
−
pp. 188-201, but translate his logical formalism into
 
−
cactus language, which is more efficient in regard to
 
−
the number of propositional clauses that are required.
 
  
−
A turing machine for computing the parity of a bit string
+
{| align="center" border="0" cellspacing="10" style="text-align:center; width:100%"
−
is described by means of the following Figure and Table.
+
| [[Image:Parity_Machine.jpg|400px]]
 +
|-
 +
| height="20px" valign="top" | <math>\text{Figure 3.} ~~ \text{Parity Machine}\!</math>
 +
|}
  
−
o-------------------------------------------------o
+
<br>
−
|                                                |
 
−
|                    1/1/+1                      |
 
−
|                    -------->                   |
 
−
|                /\ /        \ /\                |
 
−
|      0/0/+1  ^  0          1  ^  0/0/+1      |
 
−
|                \/|\        /|\/                |
 
−
|                  | <-------- |                  |
 
−
|          #/#/-1  |  1/1/+1  |  #/#/-1          |
 
−
|                  |          |                  |
 
−
|                  v          v                  |
 
−
|                  #          *                  |
 
−
|                                                |
 
−
o-------------------------------------------------o
 
−
Figure 21-a.  Parity Machine
 
  
−
Table 21-b.  Parity Machine
+
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 +
Table 4.  Parity Machine
 
o-------o--------o-------------o---------o------------o
 
o-------o--------o-------------o---------o------------o
 
| State | Symbol | Next Symbol | Ratchet | Next State |
 
| State | Symbol | Next Symbol | Ratchet | Next State |
Line 1,731: Line 1,993:
 
|  1  |  #    |    #      |  -1    |    *      |
 
|  1  |  #    |    #      |  -1    |    *      |
 
o-------o--------o-------------o---------o------------o
 
o-------o--------o-------------o---------o------------o
 +
</pre>
 +
|}
  
−
The TM has a "finite automaton" (FA) as one component.
+
<br>
−
Let us refer to this particular FA by the name of "M".
 
−
 
 
−
The "tape-head" (that is, the "read-unit") will be called "H".
 
−
The "registers" are also called "tape-cells" or "tape-squares".
 
−
</pre>
 
  
−
==Note 22==
+
The TM has a ''finite automaton'' (FA) as one component.  Let us refer to this particular FA by the name of <math>\mathrm{M}.</math>
  
−
<pre>
+
The ''tape head'' (that is, the ''read unit'') will be called <math>\mathrm{H}.</math>  The ''registers'' are also called ''tape cells'' or ''tape squares''.
−
To see how each finite approximation to a given turing machine
 
−
can be given a purely propositional description, one fixes the
 
−
parameter k and limits the rest of the discussion to describing
 
−
Stilt(k), which is not really a full-fledged TM anymore but just
 
−
a finite automaton in disguise.
 
  
−
In this example, for the sake of a minimal illustration,
+
===Finite Approximations===
−
we choose k = 2, and discuss Stunt(2).  Since the zeroth
 
−
tape cell and the last tape cell are occupied with the
 
−
bof and eof marks "#", this amounts to only one digit
 
−
of significant computation.
 
  
−
To translate Stunt(2) into propositional form we
+
To see how each finite approximation to a given turing machine can be given a purely propositional description, one fixes the parameter <math>k\!</math> and limits the rest of the discussion to describing <math>\mathrm{Stilt}(k),\!</math> which is not really a full-fledged TM anymore but just a finite automaton in disguise.
−
use the following collection of basic propositions,
 
−
boolean variables, or logical features, depending on
 
−
what one prefers to call them:
 
  
−
The basic propositions for describing the
+
In this example, for the sake of a minimal illustration, we choose <math>k = 2,\!</math> and discuss <math>\mathrm{Stunt}(2).</math>  Since the zeroth tape cell and the last tape cell are both occupied by the character <math>^{\backprime\backprime}\texttt{\#}^{\prime\prime}</math> that is used for both the ''beginning of file'' <math>(\mathrm{bof})</math> and the ''end of file'' <math>(\mathrm{eof})</math> markers, this allows for only one digit of significant computation.
−
"present state function" QF : P -> Q are
 
−
these:
 
  
−
  p0_q#, p0_q*, p0_q0, p0_q1,
+
To translate <math>\mathrm{Stunt}(2)</math> into propositional form we use the following collection of basic propositions, boolean variables, or logical features, depending on what one prefers to call them:
−
  p1_q#, p1_q*, p1_q0, p1_q1,
 
−
  p2_q#, p2_q*, p2_q0, p2_q1,
 
−
  p3_q#, p3_q*, p3_q0, p3_q1.
 
  
−
The proposition of the form pi_qj says:
+
The basic propositions for describing the ''present state function'' <math>\mathrm{QF} : P \to Q</math> are these:
  
−
  At the point-in-time p_i,
+
{| align="center" cellpadding="8" width="90%"
−
  the finite machine M is in the state q_j.
+
|
 +
<math>\begin{matrix}
 +
\texttt{p0\_q\#}, & \texttt{p0\_q*}, & \texttt{p0\_q0}, & \texttt{p0\_q1},
 +
\\[6pt]
 +
\texttt{p1\_q\#}, & \texttt{p1\_q*}, & \texttt{p1\_q0}, & \texttt{p1\_q1},
 +
\\[6pt]
 +
\texttt{p2\_q\#}, & \texttt{p2\_q*}, & \texttt{p2\_q0}, & \texttt{p2\_q1},
 +
\\[6pt]
 +
\texttt{p3\_q\#}, & \texttt{p3\_q*}, & \texttt{p3\_q0}, & \texttt{p3\_q1}.
 +
\end{matrix}</math>
 +
|}
  
−
The basic propositions for describing the
+
The proposition of the form <math>\texttt{pi\_qj}</math> says:
−
"present register function" RF : P -> R
 
−
are these:
 
  
−
  p0_r0, p0_r1, p0_r2, p0_r3,
+
{| align="center" cellpadding="8" width="90%"
−
  p1_r0, p1_r1, p1_r2, p1_r3,
+
| At the point-in-time <math>p_i,\!</math> the finite state machine <math>\mathrm{M}</math> is in the state <math>q_j.\!</math>
−
  p2_r0, p2_r1, p2_r2, p2_r3,
+
|}
−
  p3_r0, p3_r1, p3_r2, p3_r3.
 
  
−
The proposition of the form pi_rj says:
+
The basic propositions for describing the ''present register function'' <math>\mathrm{RF} : P \to R</math> are these:
  
−
  At the point-in-time p_i,
+
{| align="center" cellpadding="8" width="90%"
−
  the tape-head H is on the tape-cell r_j.
+
|
 +
<math>\begin{matrix}
 +
\texttt{p0\_r0}, & \texttt{p0\_r1}, & \texttt{p0\_r2}, & \texttt{p0\_r3},
 +
\\[6pt]
 +
\texttt{p1\_r0}, & \texttt{p1\_r1}, & \texttt{p1\_r2}, & \texttt{p1\_r3},
 +
\\[6pt]
 +
\texttt{p2\_r0}, & \texttt{p2\_r1}, & \texttt{p2\_r2}, & \texttt{p2\_r3},
 +
\\[6pt]
 +
\texttt{p3\_r0}, & \texttt{p3\_r1}, & \texttt{p3\_r2}, & \texttt{p3\_r3}.
 +
\end{matrix}</math>
 +
|}
  
−
The basic propositions for describing the
+
The proposition of the form <math>\texttt{pi\_rj}</math> says:
−
"present symbol function" SF : P -> (R -> S)
 
−
are these:
 
  
−
  p0_r0_s#, p0_r0_s*, p0_r0_s0, p0_r0_s1,
+
{| align="center" cellpadding="8" width="90%"
−
  p0_r1_s#, p0_r1_s*, p0_r1_s0, p0_r1_s1,
+
| At the point-in-time <math>p_i,\!</math> the tape head <math>\mathrm{H}</math> is on the tape cell <math>r_j.\!</math>
−
  p0_r2_s#, p0_r2_s*, p0_r2_s0, p0_r2_s1,
+
|}
−
  p0_r3_s#, p0_r3_s*, p0_r3_s0, p0_r3_s1,
 
−
  p1_r0_s#, p1_r0_s*, p1_r0_s0, p1_r0_s1,
 
−
  p1_r1_s#, p1_r1_s*, p1_r1_s0, p1_r1_s1,
 
−
  p1_r2_s#, p1_r2_s*, p1_r2_s0, p1_r2_s1,
 
−
  p1_r3_s#, p1_r3_s*, p1_r3_s0, p1_r3_s1,
 
−
  p2_r0_s#, p2_r0_s*, p2_r0_s0, p2_r0_s1,
 
−
  p2_r1_s#, p2_r1_s*, p2_r1_s0, p2_r1_s1,
 
−
  p2_r2_s#, p2_r2_s*, p2_r2_s0, p2_r2_s1,
 
−
  p2_r3_s#, p2_r3_s*, p2_r3_s0, p2_r3_s1,
 
−
  p3_r0_s#, p3_r0_s*, p3_r0_s0, p3_r0_s1,
 
−
  p3_r1_s#, p3_r1_s*, p3_r1_s0, p3_r1_s1,
 
−
  p3_r2_s#, p3_r2_s*, p3_r2_s0, p3_r2_s1,
 
−
  p3_r3_s#, p3_r3_s*, p3_r3_s0, p3_r3_s1.
 
  
−
The proposition of the form pi_rj_sk says:
+
The basic propositions for describing the ''present symbol function'' <math>\mathrm{SF} : P \to (R \to S)</math> are these:
  
−
  At the point-in-time p_i,
+
{| align="center" cellpadding="8" width="90%"
−
  the tape-cell r_j bears the mark s_k.
+
|
−
</pre>
+
<math>\begin{matrix}
 +
\texttt{p0\_r0\_s\#}, & \texttt{p0\_r0\_s*}, & \texttt{p0\_r0\_s0}, & \texttt{p0\_r0\_s1},
 +
\\[4pt]
 +
\texttt{p0\_r1\_s\#}, & \texttt{p0\_r1\_s*}, & \texttt{p0\_r1\_s0}, & \texttt{p0\_r1\_s1},
 +
\\[4pt]
 +
\texttt{p0\_r2\_s\#}, & \texttt{p0\_r2\_s*}, & \texttt{p0\_r2\_s0}, & \texttt{p0\_r2\_s1},
 +
\\[4pt]
 +
\texttt{p0\_r3\_s\#}, & \texttt{p0\_r3\_s*}, & \texttt{p0\_r3\_s0}, & \texttt{p0\_r3\_s1},
 +
\\[12pt]
 +
\texttt{p1\_r0\_s\#}, & \texttt{p1\_r0\_s*}, & \texttt{p1\_r0\_s0}, & \texttt{p1\_r0\_s1},
 +
\\[4pt]
 +
\texttt{p1\_r1\_s\#}, & \texttt{p1\_r1\_s*}, & \texttt{p1\_r1\_s0}, & \texttt{p1\_r1\_s1},
 +
\\[4pt]
 +
\texttt{p1\_r2\_s\#}, & \texttt{p1\_r2\_s*}, & \texttt{p1\_r2\_s0}, & \texttt{p1\_r2\_s1},
 +
\\[4pt]
 +
\texttt{p1\_r3\_s\#}, & \texttt{p1\_r3\_s*}, & \texttt{p1\_r3\_s0}, & \texttt{p1\_r3\_s1},
 +
\\[12pt]
 +
\texttt{p2\_r0\_s\#}, & \texttt{p2\_r0\_s*}, & \texttt{p2\_r0\_s0}, & \texttt{p2\_r0\_s1},
 +
\\[4pt]
 +
\texttt{p2\_r1\_s\#}, & \texttt{p2\_r1\_s*}, & \texttt{p2\_r1\_s0}, & \texttt{p2\_r1\_s1},
 +
\\[4pt]
 +
\texttt{p2\_r2\_s\#}, & \texttt{p2\_r2\_s*}, & \texttt{p2\_r2\_s0}, & \texttt{p2\_r2\_s1},
 +
\\[4pt]
 +
\texttt{p2\_r3\_s\#}, & \texttt{p2\_r3\_s*}, & \texttt{p2\_r3\_s0}, & \texttt{p2\_r3\_s1},
 +
\\[12pt]
 +
\texttt{p3\_r0\_s\#}, & \texttt{p3\_r0\_s*}, & \texttt{p3\_r0\_s0}, & \texttt{p3\_r0\_s1},
 +
\\[4pt]
 +
\texttt{p3\_r1\_s\#}, & \texttt{p3\_r1\_s*}, & \texttt{p3\_r1\_s0}, & \texttt{p3\_r1\_s1},
 +
\\[4pt]
 +
\texttt{p3\_r2\_s\#}, & \texttt{p3\_r2\_s*}, & \texttt{p3\_r2\_s0}, & \texttt{p3\_r2\_s1},
 +
\\[4pt]
 +
\texttt{p3\_r3\_s\#}, & \texttt{p3\_r3\_s*}, & \texttt{p3\_r3\_s0}, & \texttt{p3\_r3\_s1}.
 +
\end{matrix}</math>
 +
|}
  
−
==Note 23==
+
The proposition of the form <math>\texttt{pi\_rj\_sk}</math> says:
  
−
<pre>
+
{| align="center" cellpadding="8" width="90%"
−
Given but a single free square on the tape, there are just
+
| At the point-in-time <math>p_i,\!</math> the tape cell <math>r_j\!</math> bears the mark <math>s_k.\!</math>
−
two different sets of initial conditions for Stunt(2), the
+
|}
−
finite approximation to the parity turing machine that we
 
−
are presently considering.
 
  
−
Initial Conditions for Tape Input "0"
+
===Initial Conditions===
  
−
The following conjunction of 5 basic propositions
+
Given but a single free square on the tape, there are just two different sets of initial conditions for <math>\mathrm{Stunt}(2),</math> the finite approximation to the parity turing machine that we are presently considering.
−
describes the initial conditions when Stunt(2) is
 
−
started with an input of "0" in its free square:
 
  
−
  p0_q0
+
====Initial Conditions for Tape Input "0"====
  
−
  p0_r1
+
The following conjunction of 5 basic propositions describes the initial conditions when <math>\mathrm{Stunt}(2)</math> is started with an input of "0" in its free square:
  
−
  p0_r0_s#
+
{| align="center" cellpadding="8" width="90%"
−
  p0_r1_s0
+
|
−
  p0_r2_s#
+
<math>\begin{array}{l}
 +
\texttt{p0\_q0}
 +
\\ \\
 +
\texttt{p0\_r1}
 +
\\ \\
 +
\texttt{p0\_r0\_s\#}
 +
\\
 +
\texttt{p0\_r1\_s0}
 +
\\
 +
\texttt{p0\_r2\_s\#}
 +
\end{array}</math>
 +
|}
  
 
This conjunction of basic propositions may be read as follows:
 
This conjunction of basic propositions may be read as follows:
  
−
  At time p_0, M is in the state q_0, and
+
{| align="center" cellpadding=8" width="90%"
−
  At time p_0, H is reading cell r_1, and
+
|
−
  At time p_0, cell r_0 contains "#", and
+
<p>At time <math>p_0,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math></p>
−
  At time p_0, cell r_1 contains "0", and
+
<p>At time <math>p_0,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math></p>
−
  At time p_0, cell r_2 contains "#".
+
<p>At time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math></p>
 +
<p>At time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math></p>
 +
<p>At time <math>p_0,\!</math> cell <math>r_2\!</math> contains the symbol <math>\texttt{\#}.</math></p>
 +
|}
  
−
Initial Conditions for Tape Input "1"
+
====Initial Conditions for Tape Input "1"====
  
−
The following conjunction of 5 basic propositions
+
The following conjunction of 5 basic propositions describes the initial conditions when <math>\mathrm{Stunt}(2)</math> is started with an input of "1" in its free square:
−
describes the initial conditions when Stunt(2) is
 
−
started with an input of "1" in its free square:
 
  
−
  p0_q0
+
{| align="center" cellpadding="8" width="90%"
−
 
+
|
−
  p0_r1
+
<math>\begin{array}{l}
−
 
+
\texttt{p0\_q0}
−
  p0_r0_s#
+
\\ \\
−
  p0_r1_s1
+
\texttt{p0\_r1}
−
  p0_r2_s#
+
\\ \\
 +
\texttt{p0\_r0\_s\#}
 +
\\
 +
\texttt{p0\_r1\_s1}
 +
\\
 +
\texttt{p0\_r2\_s\#}
 +
\end{array}</math>
 +
|}
  
 
This conjunction of basic propositions may be read as follows:
 
This conjunction of basic propositions may be read as follows:
  
−
  At time p_0, M is in the state q_0, and
+
{| align="center" cellpadding=8" width="90%"
−
  At time p_0, H is reading cell r_1, and
+
|
−
  At time p_0, cell r_0 contains "#", and
+
<p>At time <math>p_0,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math></p>
−
  At time p_0, cell r_1 contains "1", and
+
<p>At time <math>p_0,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math></p>
−
  At time p_0, cell r_2 contains "#".
+
<p>At time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math></p>
−
</pre>
+
<p>At time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math></p>
 +
<p>At time <math>p_0,\!</math> cell <math>r_2\!</math> contains the symbol <math>\texttt{\#}.</math></p>
 +
|}
  
−
==Note 24==
+
===Propositional Program===
  
−
<pre>
+
A complete description of <math>\mathrm{Stunt}(2)</math> in propositional form is obtained by conjoining one of the above choices for initial conditions with all of the following sets of propositions, that serve in effect as a simple type of ''declarative program'', telling us all that we need to know about the anatomy and behavior of the truncated TM in question.
−
A complete description of Stunt(2) in propositional form is obtained by
 
−
conjoining one of the above choices for initial conditions with all of
 
−
the following sets of propositions, that serve in effect as a simple
 
−
type of "declarative program", telling us all that we need to know
 
−
about the anatomy and behavior of the truncated TM in question.
 
  
−
Mediate Conditions:
+
====Mediate Conditions====
  
−
  ( p0_q# ( p1_q# ))
+
{| align="center" cellpadding="8" width="90%"
−
  ( p0_q* ( p1_q* ))
+
|
 +
<math>\begin{array}{l}
 +
\texttt{(~p0\_q\#~(~p1\_q\#~))}
 +
\\
 +
\texttt{(~p0\_q*~(~p1\_q*~))}
 +
\\ \\
 +
\texttt{(~p1\_q\#~(~p2\_q\#~))}
 +
\\
 +
\texttt{(~p1\_q*~(~p2\_q*~))}
 +
\end{array}</math>
 +
|}
  
−
  ( p1_q# ( p2_q# ))
+
====Terminal Conditions====
−
  ( p1_q* ( p2_q* ))
 
  
−
Terminal Conditions:
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{l}
 +
\texttt{((~p2\_q\#~)(~p2\_q*~))}
 +
\end{array}</math>
 +
|}
  
−
  (( p2_q# )( p2_q* ))
+
====State Partition====
  
−
State Partition:
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{l}
 +
\texttt{((~p0\_q0~),(~p0\_q1~),(~p0\_q\#~),(~p0\_q*~))}
 +
\\
 +
\texttt{((~p1\_q0~),(~p1\_q1~),(~p1\_q\#~),(~p1\_q*~))}
 +
\\
 +
\texttt{((~p2\_q0~),(~p2\_q1~),(~p2\_q\#~),(~p2\_q*~))}
 +
\end{array}</math>
 +
|}
  
−
  (( p0_q0 ),( p0_q1 ),( p0_q# ),( p0_q* ))
+
====Register Partition====
−
  (( p1_q0 ),( p1_q1 ),( p1_q# ),( p1_q* ))
 
−
  (( p2_q0 ),( p2_q1 ),( p2_q# ),( p2_q* ))
 
  
−
Register Partition:
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{l}
 +
\texttt{((~p0\_r0~),(~p0\_r1~),(~p0\_r2~))}
 +
\\
 +
\texttt{((~p1\_r0~),(~p1\_r1~),(~p1\_r2~))}
 +
\\
 +
\texttt{((~p2\_r0~),(~p2\_r1~),(~p2\_r2~))}
 +
\end{array}</math>
 +
|}
  
−
  (( p0_r0 ),( p0_r1 ),( p0_r2 ))
+
====Symbol Partition====
−
  (( p1_r0 ),( p1_r1 ),( p1_r2 ))
 
−
  (( p2_r0 ),( p2_r1 ),( p2_r2 ))
 
  
−
Symbol Partition:
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{l}
 +
\texttt{((~p0\_r0\_s0~),(~p0\_r0\_s1~),(~p0\_r0\_s\#~))}
 +
\\
 +
\texttt{((~p0\_r1\_s0~),(~p0\_r1\_s1~),(~p0\_r1\_s\#~))}
 +
\\
 +
\texttt{((~p0\_r2\_s0~),(~p0\_r2\_s1~),(~p0\_r2\_s\#~))}
 +
\\ \\
 +
\texttt{((~p1\_r0\_s0~),(~p1\_r0\_s1~),(~p1\_r0\_s\#~))}
 +
\\
 +
\texttt{((~p1\_r1\_s0~),(~p1\_r1\_s1~),(~p1\_r1\_s\#~))}
 +
\\
 +
\texttt{((~p1\_r2\_s0~),(~p1\_r2\_s1~),(~p1\_r2\_s\#~))}
 +
\\ \\
 +
\texttt{((~p2\_r0\_s0~),(~p2\_r0\_s1~),(~p2\_r0\_s\#~))}
 +
\\
 +
\texttt{((~p2\_r1\_s0~),(~p2\_r1\_s1~),(~p2\_r1\_s\#~))}
 +
\\
 +
\texttt{((~p2\_r2\_s0~),(~p2\_r2\_s1~),(~p2\_r2\_s\#~))}
 +
\end{array}</math>
 +
|}
  
−
  (( p0_r0_s0 ),( p0_r0_s1 ),( p0_r0_s# ))
+
====Interaction Conditions====
−
  (( p0_r1_s0 ),( p0_r1_s1 ),( p0_r1_s# ))
 
−
  (( p0_r2_s0 ),( p0_r2_s1 ),( p0_r2_s# ))
 
  
−
  (( p1_r0_s0 ),( p1_r0_s1 ),( p1_r0_s# ))
+
{| align="center" cellpadding="8" width="90%"
−
  (( p1_r1_s0 ),( p1_r1_s1 ),( p1_r1_s# ))
+
|
−
  (( p1_r2_s0 ),( p1_r2_s1 ),( p1_r2_s# ))
+
<math>\begin{array}{l}
 +
\texttt{((~p0\_r0~) ~p0\_r0\_s0~  (~p1\_r0\_s0~))}
 +
\\
 +
\texttt{((~p0\_r0~) ~p0\_r0\_s1~  (~p1\_r0\_s1~))}
 +
\\
 +
\texttt{((~p0\_r0~) ~p0\_r0\_s\#~ (~p1\_r0\_s\#~))}
 +
\\ \\
 +
\texttt{((~p0\_r1~) ~p0\_r1\_s0~  (~p1\_r1\_s0~))}
 +
\\
 +
\texttt{((~p0\_r1~) ~p0\_r1\_s1~  (~p1\_r1\_s1~))}
 +
\\
 +
\texttt{((~p0\_r1~) ~p0\_r1\_s\#~ (~p1\_r1\_s\#~))}
 +
\\ \\
 +
\texttt{((~p0\_r2~) ~p0\_r2\_s0~  (~p1\_r2\_s0~))}
 +
\\
 +
\texttt{((~p0\_r2~) ~p0\_r2\_s1~  (~p1\_r2\_s1~))}
 +
\\
 +
\texttt{((~p0\_r2~) ~p0\_r2\_s\#~ (~p1\_r2\_s\#~))}
 +
\\ \\
 +
\texttt{((~p1\_r0~) ~p1\_r0\_s0~  (~p2\_r0\_s0~))}
 +
\\
 +
\texttt{((~p1\_r0~) ~p1\_r0\_s1~  (~p2\_r0\_s1~))}
 +
\\
 +
\texttt{((~p1\_r0~) ~p1\_r0\_s\#~ (~p2\_r0\_s\#~))}
 +
\\ \\
 +
\texttt{((~p1\_r1~) ~p1\_r1\_s0~  (~p2\_r1\_s0~))}
 +
\\
 +
\texttt{((~p1\_r1~) ~p1\_r1\_s1~  (~p2\_r1\_s1~))}
 +
\\
 +
\texttt{((~p1\_r1~) ~p1\_r1\_s\#~ (~p2\_r1\_s\#~))}
 +
\\ \\
 +
\texttt{((~p1\_r2~) ~p1\_r2\_s0~  (~p2\_r2\_s0~))}
 +
\\
 +
\texttt{((~p1\_r2~) ~p1\_r2\_s1~  (~p2\_r2\_s1~))}
 +
\\
 +
\texttt{((~p1\_r2~) ~p1\_r2\_s\#~ (~p2\_r2\_s\#~))}
 +
\end{array}</math>
 +
|}
  
−
  (( p2_r0_s0 ),( p2_r0_s1 ),( p2_r0_s# ))
+
====Transition Relations====
−
  (( p2_r1_s0 ),( p2_r1_s1 ),( p2_r1_s# ))
 
−
  (( p2_r2_s0 ),( p2_r2_s1 ),( p2_r2_s# ))
 
  
−
Interaction Conditions:
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{l}
 +
\texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s0~~(~p1\_q0~~p1\_r2~~p1\_r1\_s0~))}
 +
\\
 +
\texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s1~~(~p1\_q1~~p1\_r2~~p1\_r1\_s1~))}
 +
\\
 +
\texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q\#~~p1\_r0~~p1\_r1\_s\#~))}
 +
\\
 +
\texttt{(~p0\_q0~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q\#~~p1\_r1~~p1\_r2\_s\#~))}
 +
\\ \\
 +
\texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s0~~(~p1\_q1~~p1\_r2~~p1\_r1\_s0~))}
 +
\\
 +
\texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s1~~(~p1\_q0~~p1\_r2~~p1\_r1\_s1~))}
 +
\\
 +
\texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q*~~p1\_r0~~p1\_r1\_s\#~))}
 +
\\
 +
\texttt{(~p0\_q1~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q*~~p1\_r1~~p1\_r2\_s\#~))}
 +
\\ \\
 +
\texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s0~~(~p2\_q0~~p2\_r2~~p2\_r1\_s0~))}
 +
\\
 +
\texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s1~~(~p2\_q1~~p2\_r2~~p2\_r1\_s1~))}
 +
\\
 +
\texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q\#~~p2\_r0~~p2\_r1\_s\#~))}
 +
\\
 +
\texttt{(~p1\_q0~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q\#~~p2\_r1~~p2\_r2\_s\#~))}
 +
\\ \\
 +
\texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s0~~(~p2\_q1~~p2\_r2~~p2\_r1\_s0~))}
 +
\\
 +
\texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s1~~(~p2\_q0~~p2\_r2~~p2\_r1\_s1~))}
 +
\\
 +
\texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q*~~p2\_r0~~p2\_r1\_s\#~))}
 +
\\
 +
\texttt{(~p1\_q1~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q*~~p2\_r1~~p2\_r2\_s\#~))}
 +
\end{array}</math>
 +
|}
  
−
  (( p0_r0 ) p0_r0_s0 ( p1_r0_s0 ))
+
===Interpretation of the Propositional Program===
−
  (( p0_r0 ) p0_r0_s1 ( p1_r0_s1 ))
 
−
  (( p0_r0 ) p0_r0_s# ( p1_r0_s# ))
 
  
−
  (( p0_r1 ) p0_r1_s0 ( p1_r1_s0 ))
+
Let us now run through the propositional specification of <math>\mathrm{Stunt}(2),</math> our truncated TM, and paraphrase what it says in ordinary language.
−
  (( p0_r1 ) p0_r1_s1 ( p1_r1_s1 ))
 
−
  (( p0_r1 ) p0_r1_s# ( p1_r1_s# ))
 
  
−
  (( p0_r2 ) p0_r2_s0 ( p1_r2_s0 ))
+
====Mediate Conditions====
−
  (( p0_r2 ) p0_r2_s1 ( p1_r2_s1 ))
 
−
  (( p0_r2 ) p0_r2_s# ( p1_r2_s# ))
 
  
−
  (( p1_r0 ) p1_r0_s0 ( p2_r0_s0 ))
+
{| align="center" cellpadding="8" width="90%"
−
  (( p1_r0 ) p1_r0_s1 ( p2_r0_s1 ))
+
|
−
  (( p1_r0 ) p1_r0_s# ( p2_r0_s# ))
+
<math>\begin{array}{l}
 +
\texttt{(~p0\_q\#~(~p1\_q\#~))}
 +
\\
 +
\texttt{(~p0\_q*~(~p1\_q*~))}
 +
\\ \\
 +
\texttt{(~p1\_q\#~(~p2\_q\#~))}
 +
\\
 +
\texttt{(~p1\_q*~(~p2\_q*~))}
 +
\end{array}</math>
 +
|}
  
−
  (( p1_r1 ) p1_r1_s0 ( p2_r1_s0 ))
+
In the interpretation of the cactus language for propositional logic that we are using here, an expression of the form <math>\texttt{(p(q))}</math> expresses a ''conditional'', an ''implication'', or an ''if-then'' proposition, commonly read in one of the following ways:
−
  (( p1_r1 ) p1_r1_s1 ( p2_r1_s1 ))
 
−
  (( p1_r1 ) p1_r1_s# ( p2_r1_s# ))
 
  
−
  (( p1_r2 ) p1_r2_s0 ( p2_r2_s0 ))
+
{| align="center" cellpadding="8" width="90%"
−
  (( p1_r2 ) p1_r2_s1 ( p2_r2_s1 ))
+
|
−
  (( p1_r2 ) p1_r2_s# ( p2_r2_s# ))
+
<math>\begin{array}{l}
 +
\mathrm{not}~ p ~\mathrm{without}~ q
 +
\\[4pt]
 +
p ~\mathrm{implies}~ q
 +
\\[4pt]
 +
\mathrm{if}~ p ~\mathrm{then}~ q
 +
\\[4pt]
 +
p \Rightarrow q
 +
\end{array}</math>
 +
|}
  
−
Transition Relations:
+
A text string expression of the form <math>\texttt{(p(q))}</math> corresponds to a graph-theoretic data-structure of the following form:
  
−
  ( p0_q0  p0_r1  p0_r1_s0  ( p1_q0  p1_r2  p1_r1_s0 ))
+
<br>
−
  ( p0_q0  p0_r1  p0_r1_s1  ( p1_q1  p1_r2  p1_r1_s1 ))
 
−
  ( p0_q0  p0_r1  p0_r1_s#  ( p1_q#  p1_r0  p1_r1_s# ))
 
−
  ( p0_q0  p0_r2  p0_r2_s#  ( p1_q#  p1_r1  p1_r2_s# ))
 
  
−
  ( p0_q1  p0_r1  p0_r1_s0  ( p1_q1  p1_r2  p1_r1_s0 ))
+
{| align="center" border="0" cellpadding="10"
−
  ( p0_q1  p0_r1  p0_r1_s1  ( p1_q0  p1_r2  p1_r1_s1 ))
+
|
−
  ( p0_q1  p0_r1  p0_r1_s#  ( p1_q*  p1_r0  p1_r1_s# ))
+
<pre>
−
  ( p0_q1  p0_r2  p0_r2_s#  ( p1_q*  p1_r1  p1_r2_s# ))
+
o---------------------------------------o
 +
|                                      |
 +
|                p  q                |
 +
|                o---o                |
 +
|                |                    |
 +
|                @                    |
 +
|                                      |
 +
o---------------------------------------o
 +
|              ( p ( q ))             |
 +
o---------------------------------------o
 +
</pre>
 +
|}
  
−
  ( p1_q0  p1_r1  p1_r1_s0  ( p2_q0  p2_r2  p2_r1_s0 ))
+
<br>
−
  ( p1_q0  p1_r1  p1_r1_s1  ( p2_q1  p2_r2  p2_r1_s1 ))
 
−
  ( p1_q0  p1_r1  p1_r1_s#  ( p2_q#  p2_r0  p2_r1_s# ))
 
−
  ( p1_q0  p1_r2  p1_r2_s#  ( p2_q#  p2_r1  p2_r2_s# ))
 
  
−
  ( p1_q1  p1_r1  p1_r1_s0  ( p2_q1  p2_r2  p2_r1_s0 ))
+
Taken together, the Mediate Conditions state the following:
−
  ( p1_q1  p1_r1  p1_r1_s1  ( p2_q0  p2_r2  p2_r1_s1 ))
 
−
  ( p1_q1  p1_r1  p1_r1_s#  ( p2_q*  p2_r0  p2_r1_s# ))
 
−
  ( p1_q1  p1_r2  p1_r2_s#  ( p2_q*  p2_r1  p2_r2_s# ))
 
−
</pre>
 
  
−
==Note 25==
+
{| align="center" cellpadding=8" width="90%"
 +
|
 +
<p>If <math>\mathrm{M}</math> at <math>p_0\!</math> is in state <math>q_\#,\!</math> then <math>\mathrm{M}</math> at <math>p_1\!</math> is in state <math>q_\#,\!</math> and</p>
  
−
<pre>
+
<p>If <math>\mathrm{M}</math> at <math>p_0\!</math> is in state <math>q_*,\!</math> then <math>\mathrm{M}</math> at <math>p_1\!</math> is in state <math>q_*,\!</math> and</p>
−
Interpretation of the Propositional Program
 
  
−
Let us now run through the propositional specification of Stunt(2),
+
<p>If <math>\mathrm{M}</math> at <math>p_1\!</math> is in state <math>q_\#,\!</math> then <math>\mathrm{M}</math> at <math>p_2\!</math> is in state <math>q_\#,\!</math> and</p>
−
our truncated TM, and paraphrase what it says in ordinary language.
 
  
−
Mediate Conditions:
+
<p>If <math>\mathrm{M}</math> at <math>p_1\!</math> is in state <math>q_*,\!</math> then <math>\mathrm{M}</math> at <math>p_2\!</math> is in state <math>q_*.\!</math></p>
 +
|}
  
−
  ( p0_q# ( p1_q# ))
+
====Terminal Conditions====
−
  ( p0_q* ( p1_q* ))
 
  
−
  ( p1_q# ( p2_q# ))
+
{| align="center" cellpadding="8" width="90%"
−
  ( p1_q* ( p2_q* ))
+
|
 +
<math>\begin{array}{l}
 +
\texttt{((~p2\_q\#~)(~p2\_q*~))}
 +
\end{array}</math>
 +
|}
  
−
In the interpretation of the cactus language for propositional logic
+
In cactus syntax, an expression of the form <math>\texttt{((p)(q))}</math> expresses the disjunction <math>p ~\mathrm{or}~ q.</math> The corresponding cactus graph, here just a tree, has the following shape:
−
that we are using here, an expression of the form "(p (q))" expresses
 
−
a conditional, an implication, or an if-then proposition, commonly read
 
−
as: "not p without q", "if p then q", "p implies q", "p => q", and so on.
 
  
−
A text string expression of the form "(p (q))" corresponds
+
<br>
−
to a graph-theoretic data-structure of the following form:
 
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|                                       |
−
| ` ` ` ` ` ` ` ` p ` q ` ` ` ` ` ` ` ` |
+
|                 p   q                 |
−
| ` ` ` ` ` ` ` ` o---o ` ` ` ` ` ` ` ` |
+
|                 o   o                 |
−
| ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` |
+
|                 \ /                  |
−
| ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` |
+
|                  o                  |
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|                  |                  |
 +
|                   @                   |
 +
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
−
| ` ` ` ` ` ` ` ( p ( q ))` ` ` ` ` ` ` |
+
|               ((p) (q))               |
 
o---------------------------------------o
 
o---------------------------------------o
−
 
−
Taken together, the Mediate Conditions state the following:
 
−
 
−
  If M at p_0 is in state q_#, then M at p_1 is in state q_#, and
 
−
  If M at p_0 is in state q_*, then M at p_1 is in state q_*, and
 
−
  If M at p_1 is in state q_#, then M at p_2 is in state q_#, and
 
−
  If M at p_1 is in state q_*, then M at p_2 is in state q_*.
 
 
</pre>
 
</pre>
 +
|}
  
−
==Note 26==
+
<br>
  
−
<pre>
+
In effect, the Terminal Conditions state the following:
−
Interpretation of the Propositional Program (cont.)
 
  
−
Terminal Conditions:
+
{| align="center" cellpadding=8" width="90%"
 +
|
 +
<p>At time <math>p_2\!</math> machine <math>\mathrm{M}</math> is in state <math>q_\#,\!</math> or</p>
 +
<p>At time <math>p_2\!</math> machine <math>\mathrm{M}</math> is in state <math>q_*.\!</math></p>
 +
|}
  
−
  (( p2_q# )( p2_q* ))
+
====State Partition====
  
−
In cactus syntax, an expression of the form "((p)(q))"
+
{| align="center" cellpadding="8" width="90%"
−
expresses the disjunction "p or q".  The corresponding
+
|
−
cactus graph, here just a tree, has the following shape:
+
<math>\begin{array}{l}
 +
\texttt{((~p0\_q0~),(~p0\_q1~),(~p0\_q\#~),(~p0\_q*~))}
 +
\\
 +
\texttt{((~p1\_q0~),(~p1\_q1~),(~p1\_q\#~),(~p1\_q*~))}
 +
\\
 +
\texttt{((~p2\_q0~),(~p2\_q1~),(~p2\_q\#~),(~p2\_q*~))}
 +
\end{array}</math>
 +
|}
  
−
o---------------------------------------o
+
In cactus syntax, an expression of the form <math>\texttt{((} e_1 \texttt{),(} e_2 \texttt{),(} \ldots \texttt{),(} e_k \texttt{))}\!</math> expresses a statement to the effect that ''exactly one of the expressions <math>e_j\!</math> is true, for <math>j = 1 ~\mathit{to}~ k.</math>''  Expressions of this form are called ''universal partition'' expressions, and the corresponding ''painted and rooted cactus'' (PARC) has the following shape:
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
 
−
| ` ` ` ` ` ` ` ` p ` q ` ` ` ` ` ` ` ` |
 
−
| ` ` ` ` ` ` ` ` o ` o ` ` ` ` ` ` ` ` |
 
−
| ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` |
 
−
| ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` |
 
−
| ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` |
 
−
| ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` |
 
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
 
−
o---------------------------------------o
 
−
| ` ` ` ` ` ` ` ((p) (q)) ` ` ` ` ` ` ` |
 
−
o---------------------------------------o
 
  
−
In effect, the Terminal Conditions state the following:
+
<br>
−
 
 
−
  At time p_2, M is in state q_#, or
 
−
  At time p_2, M is in state q_*.
 
−
</pre>
 
−
 
 
−
==Note 27==
 
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 
<pre>
 
<pre>
−
Interpretation of the Propositional Program (cont.)
 
−
 
−
State Partition:
 
−
 
−
  (( p0_q0 ),( p0_q1 ),( p0_q# ),( p0_q* ))
 
−
  (( p1_q0 ),( p1_q1 ),( p1_q# ),( p1_q* ))
 
−
  (( p2_q0 ),( p2_q1 ),( p2_q# ),( p2_q* ))
 
−
 
−
In cactus syntax, an expression of the form "((e_1),(e_2),(...),(e_k))"
 
−
expresses the fact that "exactly one of the e_j is true, for j = 1 to k".
 
−
Expressions of this form are called "universal partition" expressions, and
 
−
the corresponding "painted and rooted cactus" (PARC) has the following shape:
 
−
 
 
o---------------------------------------o
 
o---------------------------------------o
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|                                       |
−
| ` ` ` ` e_1 ` e_2 ` ... ` e_k ` ` ` ` |
+
|         e_1   e_2   ...   e_k         |
−
| ` ` ` ` `o` ` `o` ` ` ` ` `o` ` ` ` ` |
+
|         o     o           o         |
−
| ` ` ` ` `|` ` `|` ` ` ` ` `|` ` ` ` ` |
+
|         |     |           |         |
−
| ` ` ` ` `o-----o--- ... ---o` ` ` ` ` |
+
|         o-----o--- ... ---o         |
−
| ` ` ` ` ` \ ` ` ` ` ` ` ` / ` ` ` ` ` |
+
|           \               /           |
−
| ` ` ` ` ` `\` ` ` ` ` ` `/` ` ` ` ` ` |
+
|           \             /           |
−
| ` ` ` ` ` ` \ ` ` ` ` ` / ` ` ` ` ` ` |
+
|             \           /             |
−
| ` ` ` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` |
+
|             \         /             |
−
| ` ` ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` |
+
|               \       /               |
−
| ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` |
+
|               \     /               |
−
| ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` |
+
|                 \   /                 |
−
| ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` |
+
|                 \ /                 |
−
| ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` |
+
|                   @                   |
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
−
| ` ` ` ((e_1),(e_2),(...),(e_k)) ` ` ` |
+
|       ((e_1),(e_2),(...),(e_k))       |
 
o---------------------------------------o
 
o---------------------------------------o
−
 
−
The State Partition segment of the propositional program
 
−
consists of three universal partition expressions, taken
 
−
in conjunction expressing the condition that M has to be
 
−
in one and only one of its states at each point in time
 
−
under consideration.  In short, we have the constraint:
 
−
 
−
  At each of the points in time p_i, for i in the set {0, 1, 2}
 
−
  M can be in exactly one state q_j, for j in the set {0, 1, #, *}.
 
 
</pre>
 
</pre>
 +
|}
  
−
==Note 28==
+
<br>
  
−
<pre>
+
The State Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction expressing the condition that <math>\mathrm{M}</math> has to be in one and only one of its states at each point in time under consideration.  In short, we have the constraint:
−
Interpretation of the Propositional Program (cont.)
 
  
−
Register Partition:
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<p>At each of the points in time <math>p_i,\!</math> for <math>i\!</math> in the set <math>\{ 0, 1, 2 \},\!</math></p>
  
−
  (( p0_r0 ),( p0_r1 ),( p0_r2 ))
+
<p><math>\mathrm{M}</math> can be in exactly one state <math>q_j,\!</math> for <math>j\!</math> in the set <math>\{ 0, 1, \#, * \}.\!</math></p>
−
  (( p1_r0 ),( p1_r1 ),( p1_r2 ))
+
|}
−
  (( p2_r0 ),( p2_r1 ),( p2_r2 ))
 
  
−
The Register Partition segment of the propositional program
+
====Register Partition====
−
consists of three universal partition expressions, taken in
 
−
conjunction saying that the read head H must be reading one
 
−
and only one of the registers or tape cells available to it
 
−
at each of the points in time under consideration.  In sum:
 
  
−
  At each of the points in time p_i, for i = 0, 1, 2,
+
{| align="center" cellpadding="8" width="90%"
−
  H is reading exactly one cell r_j, for j = 0, 1, 2.
+
|
−
</pre>
+
<math>\begin{array}{l}
 +
\texttt{((~p0\_r0~),(~p0\_r1~),(~p0\_r2~))}
 +
\\
 +
\texttt{((~p1\_r0~),(~p1\_r1~),(~p1\_r2~))}
 +
\\
 +
\texttt{((~p2\_r0~),(~p2\_r1~),(~p2\_r2~))}
 +
\end{array}</math>
 +
|}
  
−
==Note 29==
+
The Register Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction saying that the read head <math>\mathrm{H}</math> must be reading one and only one of the registers or tape cells available to it at each of the points in time under consideration.  In sum:
  
−
<pre>
+
{| align="center" cellpadding="8" width="90%"
−
Interpretation of the Propositional Program (cont.)
+
|
 +
<p>At each of the points in time <math>p_i,\!</math> for <math>i = 0, 1, 2,\!</math></p>
  
−
Symbol Partition:
+
<p><math>\mathrm{H}</math> is reading exactly one cell <math>r_j,\!</math> for <math>j = 0, 1, 2.\!</math>
 +
|}
  
−
  (( p0_r0_s0 ),( p0_r0_s1 ),( p0_r0_s# ))
+
====Symbol Partition====
−
  (( p0_r1_s0 ),( p0_r1_s1 ),( p0_r1_s# ))
 
−
  (( p0_r2_s0 ),( p0_r2_s1 ),( p0_r2_s# ))
 
  
−
  (( p1_r0_s0 ),( p1_r0_s1 ),( p1_r0_s# ))
+
{| align="center" cellpadding="8" width="90%"
−
  (( p1_r1_s0 ),( p1_r1_s1 ),( p1_r1_s# ))
+
|
−
  (( p1_r2_s0 ),( p1_r2_s1 ),( p1_r2_s# ))
+
<math>\begin{array}{l}
 +
\texttt{((~p0\_r0\_s0~),(~p0\_r0\_s1~),(~p0\_r0\_s\#~))}
 +
\\
 +
\texttt{((~p0\_r1\_s0~),(~p0\_r1\_s1~),(~p0\_r1\_s\#~))}
 +
\\
 +
\texttt{((~p0\_r2\_s0~),(~p0\_r2\_s1~),(~p0\_r2\_s\#~))}
 +
\\ \\
 +
\texttt{((~p1\_r0\_s0~),(~p1\_r0\_s1~),(~p1\_r0\_s\#~))}
 +
\\
 +
\texttt{((~p1\_r1\_s0~),(~p1\_r1\_s1~),(~p1\_r1\_s\#~))}
 +
\\
 +
\texttt{((~p1\_r2\_s0~),(~p1\_r2\_s1~),(~p1\_r2\_s\#~))}
 +
\\ \\
 +
\texttt{((~p2\_r0\_s0~),(~p2\_r0\_s1~),(~p2\_r0\_s\#~))}
 +
\\
 +
\texttt{((~p2\_r1\_s0~),(~p2\_r1\_s1~),(~p2\_r1\_s\#~))}
 +
\\
 +
\texttt{((~p2\_r2\_s0~),(~p2\_r2\_s1~),(~p2\_r2\_s\#~))}
 +
\end{array}</math>
 +
|}
  
−
  (( p2_r0_s0 ),( p2_r0_s1 ),( p2_r0_s# ))
+
The Symbol Partition segment of the propositional program for <math>\mathrm{Stunt}(2)</math> consists of nine universal partition expressions, taken in conjunction stipulating that there has to be one and only one symbol in each of the registers at each point in time under consideration.  In short, we have:
−
  (( p2_r1_s0 ),( p2_r1_s1 ),( p2_r1_s# ))
 
−
  (( p2_r2_s0 ),( p2_r2_s1 ),( p2_r2_s# ))
 
  
−
The Symbol Partition segment of the propositional program for Stunt(2)
+
{| align="center" cellpadding="8" width="90%"
−
consists of nine universal partition expressions, taken in conjunction
+
|
−
stipulating that there has to be one and only one symbol in each of the
+
<p>At each of the points in time <math>p_i,\!</math> for <math>i\!</math> in <math>\{ 0, 1, 2 \},\!</math></p>
−
registers at each point in time under consideration.  In short, we have:
 
  
−
  At each of the points in time p_i, for i in {0, 1, 2},
+
<p>in each of the tape registers <math>r_j,\!</math> for <math>j\!</math> in <math>\{ 0, 1, 2 \},\!</math></p>
−
  in each of the tape registers r_j, for j in {0, 1, 2},  
 
−
  there can be exactly one sign s_k, for k in {0, 1, #}.
 
−
</pre>
 
  
−
==Note 30==
+
<p>there can be exactly one sign <math>s_k,\!</math> for <math>k\!</math> in <math>\{ 0, 1, \# \}.\!</math></p>
 +
|}
  
−
<pre>
+
====Interaction Conditions====
−
Interpretation of the Propositional Program (cont.)
 
  
−
Interaction Conditions:
+
{| align="center" cellpadding="8" width="90%"
−
 
+
|
−
  (( p0_r0 ) p0_r0_s0 ( p1_r0_s0 ))
+
<math>\begin{array}{l}
−
  (( p0_r0 ) p0_r0_s1 ( p1_r0_s1 ))
+
\texttt{((~p0\_r0~) ~p0\_r0\_s0~  (~p1\_r0\_s0~))}
−
  (( p0_r0 ) p0_r0_s# ( p1_r0_s# ))
+
\\
−
 
+
\texttt{((~p0\_r0~) ~p0\_r0\_s1~  (~p1\_r0\_s1~))}
−
  (( p0_r1 ) p0_r1_s0 ( p1_r1_s0 ))
+
\\
−
  (( p0_r1 ) p0_r1_s1 ( p1_r1_s1 ))
+
\texttt{((~p0\_r0~) ~p0\_r0\_s\#~ (~p1\_r0\_s\#~))}
−
  (( p0_r1 ) p0_r1_s# ( p1_r1_s# ))
+
\\ \\
−
 
+
\texttt{((~p0\_r1~) ~p0\_r1\_s0~  (~p1\_r1\_s0~))}
−
  (( p0_r2 ) p0_r2_s0 ( p1_r2_s0 ))
+
\\
−
  (( p0_r2 ) p0_r2_s1 ( p1_r2_s1 ))
+
\texttt{((~p0\_r1~) ~p0\_r1\_s1~  (~p1\_r1\_s1~))}
−
  (( p0_r2 ) p0_r2_s# ( p1_r2_s# ))
+
\\
−
 
+
\texttt{((~p0\_r1~) ~p0\_r1\_s\#~ (~p1\_r1\_s\#~))}
−
  (( p1_r0 ) p1_r0_s0 ( p2_r0_s0 ))
+
\\ \\
−
  (( p1_r0 ) p1_r0_s1 ( p2_r0_s1 ))
+
\texttt{((~p0\_r2~) ~p0\_r2\_s0~  (~p1\_r2\_s0~))}
−
  (( p1_r0 ) p1_r0_s# ( p2_r0_s# ))
+
\\
−
 
+
\texttt{((~p0\_r2~) ~p0\_r2\_s1~  (~p1\_r2\_s1~))}
−
  (( p1_r1 ) p1_r1_s0 ( p2_r1_s0 ))
+
\\
−
  (( p1_r1 ) p1_r1_s1 ( p2_r1_s1 ))
+
\texttt{((~p0\_r2~) ~p0\_r2\_s\#~ (~p1\_r2\_s\#~))}
−
  (( p1_r1 ) p1_r1_s# ( p2_r1_s# ))
+
\\ \\
−
 
+
\texttt{((~p1\_r0~) ~p1\_r0\_s0~  (~p2\_r0\_s0~))}
−
  (( p1_r2 ) p1_r2_s0 ( p2_r2_s0 ))
+
\\
−
  (( p1_r2 ) p1_r2_s1 ( p2_r2_s1 ))
+
\texttt{((~p1\_r0~) ~p1\_r0\_s1~  (~p2\_r0\_s1~))}
−
  (( p1_r2 ) p1_r2_s# ( p2_r2_s# ))
+
\\
 +
\texttt{((~p1\_r0~) ~p1\_r0\_s\#~ (~p2\_r0\_s\#~))}
 +
\\ \\
 +
\texttt{((~p1\_r1~) ~p1\_r1\_s0~  (~p2\_r1\_s0~))}
 +
\\
 +
\texttt{((~p1\_r1~) ~p1\_r1\_s1~  (~p2\_r1\_s1~))}
 +
\\
 +
\texttt{((~p1\_r1~) ~p1\_r1\_s\#~ (~p2\_r1\_s\#~))}
 +
\\ \\
 +
\texttt{((~p1\_r2~) ~p1\_r2\_s0~  (~p2\_r2\_s0~))}
 +
\\
 +
\texttt{((~p1\_r2~) ~p1\_r2\_s1~  (~p2\_r2\_s1~))}
 +
\\
 +
\texttt{((~p1\_r2~) ~p1\_r2\_s\#~ (~p2\_r2\_s\#~))}
 +
\end{array}</math>
 +
|}
  
−
In briefest terms, the Interaction Conditions merely express
+
In briefest terms, the Interaction Conditions simply express the circumstance that the mark on a tape cell cannot change between two points in time unless the tape head is over the cell in question at the initial one of those points in time. All that we have to do is to see how they manage to say this.
−
the circumstance that the mark on a tape cell cannot change
 
−
between two points in time unless the tape head is over the
 
−
cell in question at the initial one of those points in time.
 
−
All that we have to do is to see how they manage to say this.
 
  
 
Consider a cactus expression of the following form:
 
Consider a cactus expression of the following form:
  
−
  (( p<i>_r<j> ) p<i>_r<j>_s<k> ( p<i+1>_r<j>_s<k> ))
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{array}{l}
 +
\texttt{((}~ p_i\_r_j ~\texttt{)}~ p_i\_r_j\_s_k ~\texttt{(}~ p_{i+1}\_r_j\_s_k ~\texttt{))}
 +
\end{array}</math>
 +
|}
  
 
This expression has the corresponding cactus graph:
 
This expression has the corresponding cactus graph:
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o---------------------------------------o
 
o---------------------------------------o
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|                                       |
−
| ` ` ` ` p<i>_r<j> ` p<i+1>_r<j>_s<k>` |
+
|         p<i>_r<j>   p<i+1>_r<j>_s<k> |
−
| ` ` ` ` ` ` ` ` o ` o ` ` ` ` ` ` ` ` |
+
|                 o   o                 |
−
| ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` |
+
|                 \ /                 |
−
| ` `p<i>_r<j>_s<k> o ` ` ` ` ` ` ` ` ` |
+
|   p<i>_r<j>_s<k> o                   |
−
| ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` |
+
|                   |                   |
−
| ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` |
+
|                   @                   |
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|                                       |
 
o---------------------------------------o
 
o---------------------------------------o
 +
</pre>
 +
|}
  
 
A propositional expression of this form can be read as follows:
 
A propositional expression of this form can be read as follows:
  
−
  IF:
+
{| align="center" cellpadding="8" width="90%"
 +
|<math>\mathrm{If}</math>
 +
|-
 +
| At the time <math>p_i,\!</math> the tape cell <math>r_j\!</math> bears the mark <math>s_k,\!</math>
 +
|-
 +
| <math>\mathrm{But}</math> it is not the case that:
 +
|-
 +
| At the time <math>p_i,\!</math> the tape head is on the tape cell <math>r_j,\!</math>
 +
|-
 +
| <math>\mathrm{Then}</math>
 +
|-
 +
| At the time <math>p_{i+1},\!</math> the tape cell <math>r_j\!</math> bears the mark <math>s_k.\!</math>
 +
|}
  
−
  At the time p<i>, the tape cell r<j> bears the mark s<k>,
+
The eighteen clauses of the Interaction Conditions simply impose one such constraint on symbol changes for each combination of the times <math>p_0, p_1,\!</math> registers <math>r_0, r_1, r_2,\!</math> and symbols <math>s_0, s_1, s_\#.\!</math>
  
−
  BUT it is NOT the case that:
+
====Transition Relations====
  
−
  At the time p<i>, the tape head is on the tape cell r<j>,
+
{| align="center" cellpadding="8" width="90%"
−
 
+
|
−
  THEN:
+
<math>\begin{array}{l}
−
 
+
\texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s0~~(~p1\_q0~~p1\_r2~~p1\_r1\_s0~))}
−
  At the time p<i+1>, the tape cell r<j> bears the mark s<k>.
+
\\
−
 
+
\texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s1~~(~p1\_q1~~p1\_r2~~p1\_r1\_s1~))}
−
The eighteen clauses of the Interaction Conditions simply impose
+
\\
−
one such constraint on symbol changes for each combination of the
+
\texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q\#~~p1\_r0~~p1\_r1\_s\#~))}
−
times p_0, p_1, registers r_0, r_1, r_2, and symbols s_0, s_1, s_#.
+
\\
−
</pre>
+
\texttt{(~p0\_q0~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q\#~~p1\_r1~~p1\_r2\_s\#~))}
−
 
+
\\ \\
−
==Note 31==
+
\texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s0~~(~p1\_q1~~p1\_r2~~p1\_r1\_s0~))}
−
 
+
\\
−
<pre>
+
\texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s1~~(~p1\_q0~~p1\_r2~~p1\_r1\_s1~))}
−
Interpretation of the Propositional Program (cont.)
+
\\
−
 
+
\texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q*~~p1\_r0~~p1\_r1\_s\#~))}
−
Transition Relations:
+
\\
−
 
+
\texttt{(~p0\_q1~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q*~~p1\_r1~~p1\_r2\_s\#~))}
−
  ( p0_q0  p0_r1  p0_r1_s0  ( p1_q0  p1_r2  p1_r1_s0 ))
+
\\ \\
−
  ( p0_q0  p0_r1  p0_r1_s1  ( p1_q1  p1_r2  p1_r1_s1 ))
+
\texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s0~~(~p2\_q0~~p2\_r2~~p2\_r1\_s0~))}
−
  ( p0_q0  p0_r1  p0_r1_s# ( p1_q# p1_r0  p1_r1_s# ))
+
\\
−
  ( p0_q0  p0_r2  p0_r2_s# ( p1_q# p1_r1  p1_r2_s# ))
+
\texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s1~~(~p2\_q1~~p2\_r2~~p2\_r1\_s1~))}
−
 
+
\\
−
  ( p0_q1  p0_r1  p0_r1_s0  ( p1_q1  p1_r2  p1_r1_s0 ))
+
\texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q\#~~p2\_r0~~p2\_r1\_s\#~))}
−
  ( p0_q1  p0_r1  p0_r1_s1  ( p1_q0  p1_r2  p1_r1_s1 ))
+
\\
−
  ( p0_q1  p0_r1  p0_r1_s# ( p1_q* p1_r0  p1_r1_s# ))
+
\texttt{(~p1\_q0~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q\#~~p2\_r1~~p2\_r2\_s\#~))}
−
  ( p0_q1  p0_r2  p0_r2_s# ( p1_q* p1_r1  p1_r2_s# ))
+
\\ \\
−
 
+
\texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s0~~(~p2\_q1~~p2\_r2~~p2\_r1\_s0~))}
−
  ( p1_q0  p1_r1  p1_r1_s0  ( p2_q0  p2_r2  p2_r1_s0 ))
+
\\
−
  ( p1_q0  p1_r1  p1_r1_s1  ( p2_q1  p2_r2  p2_r1_s1 ))
+
\texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s1~~(~p2\_q0~~p2\_r2~~p2\_r1\_s1~))}
−
  ( p1_q0  p1_r1  p1_r1_s# ( p2_q# p2_r0  p2_r1_s# ))
+
\\
−
  ( p1_q0  p1_r2  p1_r2_s# ( p2_q# p2_r1  p2_r2_s# ))
+
\texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q*~~p2\_r0~~p2\_r1\_s\#~))}
−
 
+
\\
−
  ( p1_q1  p1_r1  p1_r1_s0  ( p2_q1  p2_r2  p2_r1_s0 ))
+
\texttt{(~p1\_q1~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q*~~p2\_r1~~p2\_r2\_s\#~))}
−
  ( p1_q1  p1_r1  p1_r1_s1  ( p2_q0  p2_r2  p2_r1_s1 ))
+
\end{array}</math>
−
  ( p1_q1  p1_r1  p1_r1_s# ( p2_q* p2_r0  p2_r1_s# ))
+
|}
−
  ( p1_q1  p1_r2  p1_r2_s# ( p2_q* p2_r1  p2_r2_s# ))
 
  
−
The Transition Relation segment of the propositional program
+
The Transition Relation segment of the propositional program for <math>\mathrm{Stunt}(2)</math> consists of sixteen implication statements with complex antecedents and consequents.  Taken together, these give propositional expression to the TM Figure and Table that were given at the outset.
−
for Stunt(2) consists of sixteen implication statements with
 
−
complex antecedents and consequents.  Taken together, these
 
−
give propositional expression to the TM Figure and Table
 
−
that were given at the outset.
 
  
 
Just by way of a single example, consider the clause:
 
Just by way of a single example, consider the clause:
  
−
  ( p0_q0  p0_r1  p0_r1_s1  ( p1_q1  p1_r2  p1_r1_s1 ))
+
{| align="center" cellpadding="8" width="90%"
 +
| <math>\texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s1~~(~p1\_q1~~p1\_r2~~p1\_r1\_s1~))}</math>
 +
|}
  
 
This complex implication statement can be read to say:
 
This complex implication statement can be read to say:
  
−
  IF:
+
{| align="center" cellpadding="8" width="90%"
 +
|<math>\mathrm{If}</math>
 +
|-
 +
| At the time <math>p_0,\!</math> the machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math> and
 +
|-
 +
| At the time <math>p_0,\!</math> the scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math> and
 +
|-
 +
| At the time <math>p_0,\!</math> the tape cell <math>r_1\!</math> contains a <math>\texttt{1},</math>
 +
|-
 +
| <math>\mathrm{Then}</math>
 +
|-
 +
| At the time <math>p_1,\!</math> the machine <math>\mathrm{M}</math> is in the state <math>q_1,\!</math> and
 +
|-
 +
| At the time <math>p_1,\!</math> the scanner <math>\mathrm{H}</math> is reading cell <math>r_2,\!</math> and
 +
|-
 +
| At the time <math>p_1,\!</math> the tape cell <math>r_1\!</math> contains a <math>\texttt{1}.</math>
 +
|}
  
−
  At time p_0, M is in the state q_0, and
+
===Computation===
−
  At time p_0, H is reading cell r_1, and
 
−
  At time p_0, cell r_1 contains "1",
 
  
−
  THEN:
+
The propositional program for <math>\mathrm{Stunt}(2)</math> uses the following set
 +
of <math>9 + 12 + 36 = 57\!</math> basic propositions or boolean variables:
  
−
  At time p_1, M is in the state q_1, and
+
{| align="center" cellpadding="8" width="90%"
−
  At time p_1, H is reading cell r_2, and
+
|
−
  At time p_1, cell r_1 contains "1".
+
<math>\begin{matrix}
−
</pre>
+
\texttt{p0\_r0}, & \texttt{p0\_r1}, & \texttt{p0\_r2},
 +
\\[6pt]
 +
\texttt{p1\_r0}, & \texttt{p1\_r1}, & \texttt{p1\_r2},
 +
\\[6pt]
 +
\texttt{p2\_r0}, & \texttt{p2\_r1}, & \texttt{p2\_r2}.
 +
\end{matrix}</math>
 +
|}
  
−
==Note 32==
+
{| align="center" cellpadding="8" width="90%"
 +
|
 +
<math>\begin{matrix}
 +
\texttt{p0\_q\#}, & \texttt{p0\_q*}, & \texttt{p0\_q0}, & \texttt{p0\_q1},
 +
\\[6pt]
 +
\texttt{p1\_q\#}, & \texttt{p1\_q*}, & \texttt{p1\_q0}, & \texttt{p1\_q1},
 +
\\[6pt]
 +
\texttt{p2\_q\#}, & \texttt{p2\_q*}, & \texttt{p2\_q0}, & \texttt{p2\_q1}.
 +
\end{matrix}</math>
 +
|}
  
−
<pre>
+
{| align="center" cellpadding="8" width="90%"
−
Interpretation of the Propositional Program (cont.)
+
|
 +
<math>\begin{matrix}
 +
\texttt{p0\_r0\_s\#}, & \texttt{p0\_r0\_s*}, & \texttt{p0\_r0\_s0}, & \texttt{p0\_r0\_s1},
 +
\\[4pt]
 +
\texttt{p0\_r1\_s\#}, & \texttt{p0\_r1\_s*}, & \texttt{p0\_r1\_s0}, & \texttt{p0\_r1\_s1},
 +
\\[4pt]
 +
\texttt{p0\_r2\_s\#}, & \texttt{p0\_r2\_s*}, & \texttt{p0\_r2\_s0}, & \texttt{p0\_r2\_s1},
 +
\\[12pt]
 +
\texttt{p1\_r0\_s\#}, & \texttt{p1\_r0\_s*}, & \texttt{p1\_r0\_s0}, & \texttt{p1\_r0\_s1},
 +
\\[4pt]
 +
\texttt{p1\_r1\_s\#}, & \texttt{p1\_r1\_s*}, & \texttt{p1\_r1\_s0}, & \texttt{p1\_r1\_s1},
 +
\\[4pt]
 +
\texttt{p1\_r2\_s\#}, & \texttt{p1\_r2\_s*}, & \texttt{p1\_r2\_s0}, & \texttt{p1\_r2\_s1},
 +
\\[12pt]
 +
\texttt{p2\_r0\_s\#}, & \texttt{p2\_r0\_s*}, & \texttt{p2\_r0\_s0}, & \texttt{p2\_r0\_s1},
 +
\\[4pt]
 +
\texttt{p2\_r1\_s\#}, & \texttt{p2\_r1\_s*}, & \texttt{p2\_r1\_s0}, & \texttt{p2\_r1\_s1},
 +
\\[4pt]
 +
\texttt{p2\_r2\_s\#}, & \texttt{p2\_r2\_s*}, & \texttt{p2\_r2\_s0}, & \texttt{p2\_r2\_s1}.
 +
\end{matrix}</math>
 +
|}
  
−
The propositional program for Stunt(2) uses the following set
+
This means that the propositional program itself is nothing but a single proposition or boolean function of the form <math>p : \mathbb{B}^{57} \to \mathbb{B}.</math>
−
of (9 + 12 + 36) = 57 basic propositions or boolean variables:
 
  
−
  p0_r0, p0_r1, p0_r2,
+
An assignment of boolean values to the above set of boolean variables is called an ''interpretation'' of the proposition <math>p,\!</math> and any interpretation of <math>p\!</math> that makes the proposition <math>p : \mathbb{B}^{57} \to \mathbb{B}</math> evaluate to <math>1\!</math> is referred to as a ''satisfying interpretation'' of the proposition <math>p.\!</math>  Another way to specify interpretations, instead of giving them as bit vectors in <math>\mathbb{B}^{57}</math> and trying to remember some arbitrary ordering of variables, is to give them in the form of ''singular propositions'', that is, a conjunction of the form <math>e_1 \cdot \ldots \cdot e_{57}</math> where each <math>e_j\!</math> is either <math>v_j\!</math> or <math>\texttt{(} v_j \texttt{)},</math> that is, either the assertion or the negation of the boolean variable <math>{v_j},\!</math> as <math>j\!</math> runs from 1 to 57.  Even more briefly, the same information can be communicated simply by giving the conjunction of the asserted variables, with the understanding that each of the others is negated.
−
  p1_r0, p1_r1, p1_r2,
 
−
  p2_r0, p2_r1, p2_r2.
 
  
−
  p0_q#, p0_q*, p0_q0, p0_q1,
+
A satisfying interpretation of the proposition <math>p\!</math> supplies us with all the information of a complete execution history for the corresponding program, and so all we have to do in order to get the output of the program <math>p\!</math> is to read off the proper part of the data from the expression of this interpretation.
−
  p1_q#, p1_q*, p1_q0, p1_q1,
 
−
  p2_q#, p2_q*, p2_q0, p2_q1.
 
  
−
  p0_r0_s#, p0_r0_s*, p0_r0_s0, p0_r0_s1,
+
===Output===
−
  p0_r1_s#, p0_r1_s*, p0_r1_s0, p0_r1_s1,
 
−
  p0_r2_s#, p0_r2_s*, p0_r2_s0, p0_r2_s1,
 
  
−
  p1_r0_s#, p1_r0_s*, p1_r0_s0, p1_r0_s1,
+
One component of the <math>\begin{smallmatrix}\mathrm{Theme~One}\end{smallmatrix}</math> program that I wrote some years ago finds all the satisfying interpretations of propositions expressed in cactus syntax.  It's not a polynomial time algorithm, as you may guess, but it was just barely efficient enough to do this example in the 500 K of spare memory that I had on an old 286 PC in about 1989, so I will give you the actual outputs from those trials.
−
  p1_r1_s#, p1_r1_s*, p1_r1_s0, p1_r1_s1,
 
−
  p1_r2_s#, p1_r2_s*, p1_r2_s0, p1_r2_s1,
 
  
−
  p2_r0_s#, p2_r0_s*, p2_r0_s0, p2_r0_s1,
+
====Output Conditions for Tape Input "0"====
−
  p2_r1_s#, p2_r1_s*, p2_r1_s0, p2_r1_s1,
 
−
  p2_r2_s#, p2_r2_s*, p2_r2_s0, p2_r2_s1.
 
  
−
This means that the propositional program itself is nothing more or
+
Let <math>p_0\!</math> be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "0" with the proposition that describes the truncated turing machine <math>\mathrm{Stunt}(2).</math>  As it turns out, <math>p_0\!</math> has a single satisfying interpretation.  This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display:
−
less than a single proposition or a boolean function P : B^57 -> B.
 
  
−
An assignment of boolean values to the above set of boolean variables
+
<br>
−
is called an "interpretation" of P, and any interpretation of P that
 
−
makes the proposition P : B^57 -> B evaluate to 1 is referred to as
 
−
a "satisfying interpretation" of the proposition P.  Another way to
 
−
specify interpretations, instead of giving them as bit vectors in
 
−
B^57 and trying to remember some arbitrary ordering of variables,
 
−
is to give them in the form of "singular propositions", that is,
 
−
a conjunction of the form "e_1 & ... & e_57" where each e_j is
 
−
either "v_j" or "(v_j)", that is, either the assertion or the
 
−
negation of the boolean variable v_j, as j runs from 1 to 57.
 
−
Even more briefly, the same information can be communicated
 
−
simply by giving the conjunction of the asserted variables,
 
−
with the understanding that each of the others is negated.
 
−
 
 
−
A satisfying interpretation of the proposition P supplies us
 
−
with all the information of a complete execution history for
 
−
the corresponding program, and so all we have to do in order
 
−
to get the output of the program P is to read off the proper
 
−
part of the data from the expression of this interpretation.
 
−
</pre>
 
−
 
 
−
==Note 33==
 
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 
<pre>
 
<pre>
−
Interpretation of the Propositional Program (concl.)
 
−
 
−
One component of the Theme One program that I wrote some years ago
 
−
finds all the satisfying interpretations of propositions expressed
 
−
in cactus syntax.  It's not a polynomial time algorithm, as you may
 
−
guess, but it was just barely efficient enough to do this example
 
−
in the 500 K of spare memory that I had on an old 286 PC in about
 
−
1989, so I will give you the actual outputs from those trials.
 
−
 
−
Output Conditions for Tape Input "0"
 
−
 
−
Let P_0 be the proposition that we get by conjoining
 
−
the proposition that describes the initial conditions
 
−
for tape input "0" with the proposition that describes
 
−
the truncated turing machine Stunt(2).  As it turns out,
 
−
P_0 has a single satisfying interpretation, and this is
 
−
represented as a singular proposition in terms of its
 
−
positive logical features in the following display:
 
−
 
 
o-------------------------------------------------o
 
o-------------------------------------------------o
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|                                                 |
−
| p0_q0 ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
| p0_q0                                           |
−
| `p0_r1` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
| p0_r1                                         |
−
| ` p0_r0_s#` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|   p0_r0_s#                                     |
−
| ` `p0_r1_s0 ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|   p0_r1_s0                                     |
−
| ` ` p0_r2_s#` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|     p0_r2_s#                                   |
−
| ` ` `p1_q0` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|     p1_q0                                     |
−
| ` ` ` p1_r2 ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|       p1_r2                                     |
−
| ` ` ` `p1_r2_s# ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|       p1_r2_s#                                 |
−
| ` ` ` ` p1_r0_s#` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|         p1_r0_s#                               |
−
| ` ` ` ` `p1_r1_s0 ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|         p1_r1_s0                               |
−
| ` ` ` ` ` p2_q# ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|           p2_q#                                 |
−
| ` ` ` ` ` `p2_r1` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|           p2_r1                               |
−
| ` ` ` ` ` ` p2_r0_s#` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|             p2_r0_s#                           |
−
| ` ` ` ` ` ` `p2_r1_s0 ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|             p2_r1_s0                           |
−
| ` ` ` ` ` ` ` p2_r2_s#` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|               p2_r2_s#                         |
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|                                                 |
 
o-------------------------------------------------o
 
o-------------------------------------------------o
 +
</pre>
 +
|}
 +
 +
<br>
  
 
The Output Conditions for Tape Input "0" can be read as follows:
 
The Output Conditions for Tape Input "0" can be read as follows:
  
−
  At the time p_0, M is in the state q_0, and
+
{| align="center" cellpadding=8" width="90%"
−
  At the time p_0, H is reading cell r_1, and
+
|
−
  At the time p_0, cell r_0 contains "#", and
+
<p>At the time <math>p_0,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math> and</p>
−
  At the time p_0, cell r_1 contains "0", and
+
<p>At the time <math>p_0,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math> and</p>
−
  At the time p_0, cell r_2 contains "#", and
+
<p>At the time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 +
<p>At the time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math> and</p>
 +
<p>At the time <math>p_0,\!</math> cell <math>r_2\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 +
|-
 +
|
 +
<p>At the time <math>p_1,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math> and</p>
 +
<p>At the time <math>p_1,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_2,\!</math> and</p>
 +
<p>At the time <math>p_1,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 +
<p>At the time <math>p_1,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math> and</p>
 +
<p>At the time <math>p_1,\!</math> cell <math>r_2\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 +
|-
 +
|
 +
<p>At the time <math>p_2,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_\#,\!</math> and</p>
 +
<p>At the time <math>p_2,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math> and</p>
 +
<p>At the time <math>p_2,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 +
<p>At the time <math>p_2,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math> and</p>
 +
<p>At the time <math>p_2,\!</math> cell <math>r_2\!</math> contains the symbol <math>\texttt{\#}.</math></p>
 +
|}
  
−
  At the time p_1, M is in the state q_0, and
+
The output of <math>\mathrm{Stunt}(2)</math> being the symbol that rests under the tape head <math>\mathrm{H}</math> if and when the machine <math>\mathrm{M}</math> reaches one of its resting states, we get the result that <math>\mathrm{Parity}(0) = 0.</math>
−
  At the time p_1, H is reading cell r_2, and
 
−
  At the time p_1, cell r_0 contains "#", and
 
−
  At the time p_1, cell r_1 contains "0", and
 
−
  At the time p_1, cell r_2 contains "#", and
 
  
−
  At the time p_2, M is in the state q_#, and
+
====Output Conditions for Tape Input "1"====
−
  At the time p_2, H is reading cell r_1, and
 
−
  At the time p_2, cell r_0 contains "#", and
 
−
  At the time p_2, cell r_1 contains "0", and
 
−
  At the time p_2, cell r_2 contains "#".
 
  
−
The output of Stunt(2) being the symbol that rests under
+
Let <math>p_1\!</math> be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "1" with the proposition that describes the truncated turing machine <math>\mathrm{Stunt}(2).</math>  As it turns out, <math>p_1\!</math> has a single satisfying interpretation.  This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display:
−
the tape head H if and when the machine M reaches one of
 
−
its resting states, we get the result that Parity(0) = 0.
 
  
−
Output Conditions for Tape Input "1"
+
<br>
−
 
 
−
Let P_1 be the proposition that we get by conjoining
 
−
the proposition that describes the initial conditions
 
−
for tape input "1" with the proposition that describes
 
−
the truncated turing machine Stunt(2).  As it turns out,
 
−
P_1 has a single satisfying interpretation, and this is
 
−
represented as a singular proposition in terms of its
 
−
positive logical features in the following display:
 
  
 +
{| align="center" border="0" cellpadding="10"
 +
|
 +
<pre>
 
o-------------------------------------------------o
 
o-------------------------------------------------o
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|                                                 |
−
| p0_q0 ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
| p0_q0                                           |
−
| `p0_r1` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
| p0_r1                                         |
−
| ` p0_r0_s#` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|   p0_r0_s#                                     |
−
| ` `p0_r1_s1 ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|   p0_r1_s1                                     |
−
| ` ` p0_r2_s#` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|     p0_r2_s#                                   |
−
| ` ` `p1_q1` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|     p1_q1                                     |
−
| ` ` ` p1_r2 ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|       p1_r2                                     |
−
| ` ` ` `p1_r2_s# ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|       p1_r2_s#                                 |
−
| ` ` ` ` p1_r0_s#` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|         p1_r0_s#                               |
−
| ` ` ` ` `p1_r1_s1 ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|         p1_r1_s1                               |
−
| ` ` ` ` ` p2_q* ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|           p2_q*                                 |
−
| ` ` ` ` ` `p2_r1` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|           p2_r1                               |
−
| ` ` ` ` ` ` p2_r0_s#` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|             p2_r0_s#                           |
−
| ` ` ` ` ` ` `p2_r1_s1 ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|             p2_r1_s1                           |
−
| ` ` ` ` ` ` ` p2_r2_s#` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|               p2_r2_s#                         |
−
| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` |
+
|                                                 |
 
o-------------------------------------------------o
 
o-------------------------------------------------o
−
 
−
The Output Conditions for Tape Input "1" can be read as follows:
 
−
 
−
  At the time p_0, M is in the state q_0, and
 
−
  At the time p_0, H is reading cell r_1, and
 
−
  At the time p_0, cell r_0 contains "#", and
 
−
  At the time p_0, cell r_1 contains "1", and
 
−
  At the time p_0, cell r_2 contains "#", and
 
−
 
−
  At the time p_1, M is in the state q_1, and
 
−
  At the time p_1, H is reading cell r_2, and
 
−
  At the time p_1, cell r_0 contains "#", and
 
−
  At the time p_1, cell r_1 contains "1", and
 
−
  At the time p_1, cell r_2 contains "#", and
 
−
 
−
  At the time p_2, M is in the state q_*, and
 
−
  At the time p_2, H is reading cell r_1, and
 
−
  At the time p_2, cell r_0 contains "#", and
 
−
  At the time p_2, cell r_1 contains "1", and
 
−
  At the time p_2, cell r_2 contains "#".
 
−
 
−
The output of Stunt(2) being the symbol that rests under
 
−
the tape head H when and if the machine M reaches one of
 
−
its resting states, we get the result that Parity(1) = 1.
 
 
</pre>
 
</pre>
 +
|}
  
−
==Work Area==
+
<br>
  
−
<pre>
+
The Output Conditions for Tape Input "1" can be read as follows:
−
DATA 20.  http://forum.wolframscience.com/showthread.php?postid=791#post791
 
  
−
Let's see how this information about the transformation F,
+
{| align="center" cellpadding=8" width="90%"
−
arrived at by eyeballing the raw data, comports with what
+
|
−
we derived through a more systematic symbolic computation.
+
<p>At the time <math>p_0,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math> and</p>
−
 
+
<p>At the time <math>p_0,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math> and</p>
−
The results of the various operator actions that we have just
+
<p>At the time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
−
computed are summarized in Tables 66-i and 66-ii from my paper,
+
<p>At the time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math> and</p>
−
and I have attached these as a text file below.
+
<p>At the time <math>p_0,\!</math> cell <math>r_2\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
−
 
+
|-
−
Table 66-i.  Computation Summary for f<u, v> = ((u)(v))
+
|
−
o--------------------------------------------------------------------------------o
+
<p>At the time <math>p_1,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_1,\!</math> and</p>
−
|                                                                                |
+
<p>At the time <math>p_1,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_2,\!</math> and</p>
−
| !e!f  = uv.    1      + u(v).    1      + (u)v.    1      + (u)(v).    0      |
+
<p>At the time <math>p_1,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
−
|                                                                                |
+
<p>At the time <math>p_1,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math> and</p>
−
|  Ef  = uv. (du  dv)  + u(v). (du (dv)) + (u)v.((du) dv)  + (u)(v).((du)(dv)) |
+
<p>At the time <math>p_1,\!</math> cell <math>r_2\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
−
|                                                                                |
+
|-
−
|  Df  = uv.  du  dv  + u(v).  du (dv)  + (u)v. (du) dv  + (u)(v).((du)(dv)) |
+
|
−
|                                                                                |
+
<p>At the time <math>p_2,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_*,\!</math> and</p>
−
|  df  =  uv.    0      + u(v).  du      + (u)v.      dv  + (u)(v). (du, dv)  |
+
<p>At the time <math>p_2,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math> and</p>
−
|                                                                                |
+
<p>At the time <math>p_2,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
−
|  rf  =  uv.  du  dv  + u(v).  du  dv  + (u)v.  du  dv  + (u)(v).  du  dv  |
+
<p>At the time <math>p_2,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math> and</p>
−
|                                                                                |
+
<p>At the time <math>p_2,\!</math> cell <math>r_2\!</math> contains the symbol <math>\texttt{\#}.</math></p>
−
o--------------------------------------------------------------------------------o
+
|}
−
 
 
−
Table 66-ii.  Computation Summary for g<u, v> = ((u, v))
 
−
o--------------------------------------------------------------------------------o
 
−
|                                                                                |
 
−
| !e!g  =  uv.    1      + u(v).    0      + (u)v.    0      + (u)(v).    1      |
 
−
|                                                                                |
 
−
|  Eg  =  uv.((du, dv)) + u(v). (du, dv)  + (u)v. (du, dv)  + (u)(v).((du, dv)) |
 
−
|                                                                                |
 
−
|  Dg  =  uv. (du, dv)  + u(v). (du, dv)  + (u)v. (du, dv)  + (u)(v). (du, dv)  |
 
−
|                                                                                |
 
−
|  dg  =  uv. (du, dv)  + u(v). (du, dv)  + (u)v. (du, dv)  + (u)(v). (du, dv)  |
 
−
|                                                                                |
 
−
|  rg  =  uv.    0      + u(v).    0      + (u)v.    0      + (u)(v).    0      |
 
−
|                                                                                |
 
−
o--------------------------------------------------------------------------------o
 
−
 
 
−
 
 
−
o---------------------------------------o
 
−
|                                      |
 
−
|                  o                  |
 
−
|                  / \                 |
 
−
|                /   \                 |
 
−
|                /    \               |
 
−
|              o      o              |
 
−
|              / \     / \             |
 
−
|            /   \  /   \             |
 
−
|            /     \ /     \           |
 
−
|          o      o      o          |
 
−
|          / \     / \    / \          |
 
−
|        /  \   /   \   /   \         |
 
−
|        /     \ /     \ /     \       |
 
−
|      o      o      o      o      |
 
−
|      / \     / \     / \    / \      |
 
−
|     /   \   /   \   /   \  /   \     |
 
−
|    /     \ /     \ /     \ /     \    |
 
−
|  o      o      o      o      o  |
 
−
|  |\     / \     / \     / \    /|  |
 
−
|  | \   /   \   /   \   /   \  / |  |
 
−
|  |  \ /     \ /     \ /     \ / |  |
 
−
|  |  o      o      o      o  |  |
 
−
|  |  |\     / \     / \     /|  |  |
 
−
|  |  | \   /   \   /   \   / |  |  |
 
−
|  | u |  \ /     \ /     \ /  | v |  |
 
−
|  o---+---o      o      o---+---o  |
 
−
|      |    \     / \    /   |      |
 
−
|      |    \   /   \   /     |      |
 
−
|      | du  \ /     \ /   dv |      |
 
−
|      o-------o      o-------o      |
 
−
|                \     /               |
 
−
|                \   /                 |
 
−
|                  \ /                  |
 
−
|                  o                  |
 
−
|                                      |
 
−
o---------------------------------------o
 
−
</pre>
 
−
 
 
−
==Discussion==
 
−
 
 
−
<pre>
 
−
PD = Philip Dutton
 
−
 
 
−
PD: I've been watching your posts.
 
−
 
 
−
PD: I am not an expert on logic infrastructures but I find the posts
 
−
    interesting (despite not understanding much of it).  I am like
 
−
    the diagrams.  I have recently been trying to understand CA's
 
−
    using a particular perspective:  sinks and sources.  I think
 
−
    that all CA's are simply combinations of sinks and sources.
 
−
    How they interact (or intrude into each other's domains)
 
−
    would most likely be a result of the rules (and initial
 
−
    configuration of on or off cells).
 
−
 
 
−
PD: Anyway, to be short, I "see" diamond shapes quite often in
 
−
    your diagrams.  Triangles (either up or down) or diamonds
 
−
    (combination of an up and down triangle) make me think
 
−
    soley of sinks and sources.  I think of the diamond to
 
−
    be a source which, during the course of progression,
 
−
    is expanding (because it is producing) and then starts
 
−
    to act as a sink  (because it consumes) -- and hence the
 
−
    diamond.  I can't stop thinking about sinks and sources in
 
−
    CA's and so I thought I would ask you if there is some way
 
−
    to tie the two worlds together (CA's of sinks and sources
 
−
    together with your differential constructs).
 
  
−
PD: Any thoughts?
+
The output of <math>\mathrm{Stunt}(2)</math> being the symbol that rests under the tape head <math>\mathrm{H}</math> when and if the machine <math>\mathrm{M}</math> reaches one of its resting states, we get the result that <math>\mathrm{Parity}(1) = 1.</math>
−
 
 
−
Yes, I'm hoping that there's a lot of stuff analogous to
 
−
R-world dynamics to be discovered in this B-world variety,
 
−
indeed, that's kind of why I set out on this investigation --
 
−
oh, gee, has it been that long? -- I guess about 1989 or so,
 
−
when I started to see this "differential logic" angle on what
 
−
I had previously studied in systems theory as the "qualitative
 
−
approach to differential equations".  I think we used to use the
 
−
words "attractor" and "basin" more often than "sink", but a source
 
−
is still a source as time goes by, and I do remember using the word
 
−
"sink" a lot when I was a freshperson in physics, before I got logic.
 
−
 
 
−
I have spent the last 15 years doing a funny mix of practice in stats
 
−
and theory in math, but I did read early works by Von Neumann, Burks,
 
−
Ulam, and later stuff by Holland on CA's.  Still, it may be a while
 
−
before I have re-heated my concrete intuitions about them in the
 
−
NKS way of thinking.
 
−
 
 
−
There are some fractal-looking pictures that emerge when
 
−
I turn to "higher order propositional expressions" (HOPE's).
 
−
I have discussed this topic elswhere on the web and can look
 
−
it up now if your are interested, but I am trying to make my
 
−
e-positions somewhat clearer for the NKS forum than I have
 
−
tried to do before.
 
−
 
 
−
But do not hestitate to dialogue all this stuff on the boards,
 
−
as that's what always seems to work the best.  What I've found
 
−
works best for me, as I can hardly remember what I was writing
 
−
last month without Google, is to archive a copy at one of the
 
−
other Google-visible discussion lists that I'm on at present.
 
−
</pre>
 
  
 
==Document History==
 
==Document History==
  
−
<pre>
+
===Ontology List : Feb&ndash;Mar 2004===
−
DATA.  Differential Analytic Turing Automata
 
  
−
Ontology List
+
* http://suo.ieee.org/ontology/thrd2.html#05457
 +
# http://suo.ieee.org/ontology/msg05457.html
 +
# http://suo.ieee.org/ontology/msg05458.html
 +
# http://suo.ieee.org/ontology/msg05459.html
 +
# http://suo.ieee.org/ontology/msg05460.html
 +
# http://suo.ieee.org/ontology/msg05461.html
 +
# http://suo.ieee.org/ontology/msg05462.html
 +
# http://suo.ieee.org/ontology/msg05463.html
 +
# http://suo.ieee.org/ontology/msg05464.html
 +
# http://suo.ieee.org/ontology/msg05465.html
 +
# http://suo.ieee.org/ontology/msg05466.html
 +
# http://suo.ieee.org/ontology/msg05467.html
 +
# http://suo.ieee.org/ontology/msg05469.html
 +
# http://suo.ieee.org/ontology/msg05470.html
 +
# http://suo.ieee.org/ontology/msg05471.html
 +
# http://suo.ieee.org/ontology/msg05472.html
 +
# http://suo.ieee.org/ontology/msg05473.html
 +
# http://suo.ieee.org/ontology/msg05474.html
 +
# http://suo.ieee.org/ontology/msg05475.html
 +
# http://suo.ieee.org/ontology/msg05476.html
 +
# http://suo.ieee.org/ontology/msg05479.html
  
−
01.  http://suo.ieee.org/ontology/msg05457.html
+
===NKS Forum : Feb&ndash;Jun 2004===
−
02.  http://suo.ieee.org/ontology/msg05458.html
 
−
03.  http://suo.ieee.org/ontology/msg05459.html
 
−
04.  http://suo.ieee.org/ontology/msg05460.html
 
−
05.  http://suo.ieee.org/ontology/msg05461.html
 
−
06.  http://suo.ieee.org/ontology/msg05462.html
 
−
07.  http://suo.ieee.org/ontology/msg05463.html
 
−
08.  http://suo.ieee.org/ontology/msg05464.html
 
−
09.  http://suo.ieee.org/ontology/msg05465.html
 
−
10.  http://suo.ieee.org/ontology/msg05466.html
 
−
11.  http://suo.ieee.org/ontology/msg05467.html
 
−
12.  http://suo.ieee.org/ontology/msg05469.html
 
−
13.  http://suo.ieee.org/ontology/msg05470.html
 
−
14.  http://suo.ieee.org/ontology/msg05471.html
 
−
15.  http://suo.ieee.org/ontology/msg05472.html
 
−
16.  http://suo.ieee.org/ontology/msg05473.html
 
−
17.  http://suo.ieee.org/ontology/msg05474.html
 
−
18.  http://suo.ieee.org/ontology/msg05475.html
 
−
19.  http://suo.ieee.org/ontology/msg05476.html
 
−
20.  http://suo.ieee.org/ontology/msg05479.html
 
  
−
Inquiry List
+
* http://forum.wolframscience.com/archive/topic/228-1.html
 +
* http://forum.wolframscience.com/showthread.php?threadid=228
 +
* http://forum.wolframscience.com/printthread.php?threadid=228&perpage=50
 +
# http://forum.wolframscience.com/showthread.php?postid=664#post664
 +
# http://forum.wolframscience.com/showthread.php?postid=666#post666
 +
# http://forum.wolframscience.com/showthread.php?postid=677#post677
 +
# http://forum.wolframscience.com/showthread.php?postid=684#post684
 +
# http://forum.wolframscience.com/showthread.php?postid=689#post689
 +
# http://forum.wolframscience.com/showthread.php?postid=697#post697
 +
# http://forum.wolframscience.com/showthread.php?postid=708#post708
 +
# http://forum.wolframscience.com/showthread.php?postid=721#post721
 +
# http://forum.wolframscience.com/showthread.php?postid=722#post722
 +
# http://forum.wolframscience.com/showthread.php?postid=725#post725
 +
# http://forum.wolframscience.com/showthread.php?postid=733#post733
 +
# http://forum.wolframscience.com/showthread.php?postid=756#post756
 +
# http://forum.wolframscience.com/showthread.php?postid=759#post759
 +
# http://forum.wolframscience.com/showthread.php?postid=764#post764
 +
# http://forum.wolframscience.com/showthread.php?postid=766#post766
 +
# http://forum.wolframscience.com/showthread.php?postid=767#post767
 +
# http://forum.wolframscience.com/showthread.php?postid=773#post773
 +
# http://forum.wolframscience.com/showthread.php?postid=775#post775
 +
# http://forum.wolframscience.com/showthread.php?postid=777#post777
 +
# http://forum.wolframscience.com/showthread.php?postid=791#post791
 +
# http://forum.wolframscience.com/showthread.php?postid=1458#post1458
 +
# http://forum.wolframscience.com/showthread.php?postid=1461#post1461
 +
# http://forum.wolframscience.com/showthread.php?postid=1463#post1463
 +
# http://forum.wolframscience.com/showthread.php?postid=1464#post1464
 +
# http://forum.wolframscience.com/showthread.php?postid=1467#post1467
 +
# http://forum.wolframscience.com/showthread.php?postid=1469#post1469
 +
# http://forum.wolframscience.com/showthread.php?postid=1470#post1470
 +
# http://forum.wolframscience.com/showthread.php?postid=1471#post1471
 +
# http://forum.wolframscience.com/showthread.php?postid=1473#post1473
 +
# http://forum.wolframscience.com/showthread.php?postid=1475#post1475
 +
# http://forum.wolframscience.com/showthread.php?postid=1479#post1479
 +
# http://forum.wolframscience.com/showthread.php?postid=1489#post1489
 +
# http://forum.wolframscience.com/showthread.php?postid=1490#post1490
  
−
00.  http://stderr.org/pipermail/inquiry/2004-February/thread.html#1228
+
===Inquiry List : Feb&ndash;Jun 2004===
−
00.  http://stderr.org/pipermail/inquiry/2004-March/thread.html#1235
 
−
00.  http://stderr.org/pipermail/inquiry/2004-March/thread.html#1240
 
−
00.  http://stderr.org/pipermail/inquiry/2004-June/thread.html#1630
 
  
−
01. http://stderr.org/pipermail/inquiry/2004-February/001228.html
+
* http://stderr.org/pipermail/inquiry/2004-February/thread.html#1228
−
02.  http://stderr.org/pipermail/inquiry/2004-February/001230.html
+
* http://stderr.org/pipermail/inquiry/2004-March/thread.html#1235
−
03.  http://stderr.org/pipermail/inquiry/2004-February/001231.html
+
* http://stderr.org/pipermail/inquiry/2004-March/thread.html#1240
−
04.  http://stderr.org/pipermail/inquiry/2004-February/001232.html
+
* http://stderr.org/pipermail/inquiry/2004-June/thread.html#1630
−
05.  http://stderr.org/pipermail/inquiry/2004-February/001233.html
+
# http://stderr.org/pipermail/inquiry/2004-February/001228.html
−
06.  http://stderr.org/pipermail/inquiry/2004-February/001234.html
+
# http://stderr.org/pipermail/inquiry/2004-February/001230.html
−
07.  http://stderr.org/pipermail/inquiry/2004-March/001235.html
+
# http://stderr.org/pipermail/inquiry/2004-February/001231.html
−
08.  http://stderr.org/pipermail/inquiry/2004-March/001236.html
+
# http://stderr.org/pipermail/inquiry/2004-February/001232.html
−
09.  http://stderr.org/pipermail/inquiry/2004-March/001237.html
+
# http://stderr.org/pipermail/inquiry/2004-February/001233.html
−
10.  http://stderr.org/pipermail/inquiry/2004-March/001238.html
+
# http://stderr.org/pipermail/inquiry/2004-February/001234.html
−
11.  http://stderr.org/pipermail/inquiry/2004-March/001240.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001235.html
−
12.  http://stderr.org/pipermail/inquiry/2004-March/001242.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001236.html
−
13.  http://stderr.org/pipermail/inquiry/2004-March/001243.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001237.html
−
14.  http://stderr.org/pipermail/inquiry/2004-March/001244.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001238.html
−
15.  http://stderr.org/pipermail/inquiry/2004-March/001245.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001240.html
−
16.  http://stderr.org/pipermail/inquiry/2004-March/001246.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001242.html
−
17.  http://stderr.org/pipermail/inquiry/2004-March/001247.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001243.html
−
18.  http://stderr.org/pipermail/inquiry/2004-March/001248.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001244.html
−
19.  http://stderr.org/pipermail/inquiry/2004-March/001249.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001245.html
−
20.  http://stderr.org/pipermail/inquiry/2004-March/001255.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001246.html
−
21.  http://stderr.org/pipermail/inquiry/2004-June/001630.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001247.html
−
22.  http://stderr.org/pipermail/inquiry/2004-June/001631.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001248.html
−
23.  http://stderr.org/pipermail/inquiry/2004-June/001632.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001249.html
−
24.  http://stderr.org/pipermail/inquiry/2004-June/001633.html
+
# http://stderr.org/pipermail/inquiry/2004-March/001255.html
−
25.  http://stderr.org/pipermail/inquiry/2004-June/001634.html
+
# http://stderr.org/pipermail/inquiry/2004-June/001630.html
−
26.  http://stderr.org/pipermail/inquiry/2004-June/001635.html
+
# http://stderr.org/pipermail/inquiry/2004-June/001631.html
−
27.  http://stderr.org/pipermail/inquiry/2004-June/001636.html
+
# http://stderr.org/pipermail/inquiry/2004-June/001632.html
−
28.  http://stderr.org/pipermail/inquiry/2004-June/001637.html
+
# http://stderr.org/pipermail/inquiry/2004-June/001633.html
−
29.  http://stderr.org/pipermail/inquiry/2004-June/001638.html
+
# http://stderr.org/pipermail/inquiry/2004-June/001634.html
−
30.  http://stderr.org/pipermail/inquiry/2004-June/001639.html
+
# http://stderr.org/pipermail/inquiry/2004-June/001635.html
−
31.  http://stderr.org/pipermail/inquiry/2004-June/001640.html
+
# http://stderr.org/pipermail/inquiry/2004-June/001636.html
−
32.  http://stderr.org/pipermail/inquiry/2004-June/001641.html
+
# http://stderr.org/pipermail/inquiry/2004-June/001637.html
−
33.  http://stderr.org/pipermail/inquiry/2004-June/001642.html
+
# http://stderr.org/pipermail/inquiry/2004-June/001638.html
 +
# http://stderr.org/pipermail/inquiry/2004-June/001639.html
 +
# http://stderr.org/pipermail/inquiry/2004-June/001640.html
 +
# http://stderr.org/pipermail/inquiry/2004-June/001641.html
 +
# http://stderr.org/pipermail/inquiry/2004-June/001642.html
  
−
NKS Forum
+
[[Category:Automata Theory]]
−
 
+
[[Category:Computation]]
−
00.  http://forum.wolframscience.com/showthread.php?threadid=228
+
[[Category:Computational Complexity]]
−
01.  http://forum.wolframscience.com/showthread.php?postid=664#post664
+
[[Category:Computer Science]]
−
02.  http://forum.wolframscience.com/showthread.php?postid=666#post666
+
[[Category:Differential Logic]]
−
03.  http://forum.wolframscience.com/showthread.php?postid=677#post677
+
[[Category:Formal Languages]]
−
04.  http://forum.wolframscience.com/showthread.php?postid=684#post684
+
[[Category:Graph Theory]]
−
05.  http://forum.wolframscience.com/showthread.php?postid=689#post689
+
[[Category:Logic]]
−
06.  http://forum.wolframscience.com/showthread.php?postid=697#post697
+
[[Category:Logical Graphs]]
−
07.  http://forum.wolframscience.com/showthread.php?postid=708#post708
+
[[Category:Mathematics]]
−
08.  http://forum.wolframscience.com/showthread.php?postid=721#post721
+
[[Category:Programming Languages]]
−
09.  http://forum.wolframscience.com/showthread.php?postid=722#post722
+
[[Category:Turing Machines]]
−
10.  http://forum.wolframscience.com/showthread.php?postid=725#post725
+
[[Category:Visualization]]
−
11.  http://forum.wolframscience.com/showthread.php?postid=733#post733
 
−
12.  http://forum.wolframscience.com/showthread.php?postid=756#post756
 
−
13.  http://forum.wolframscience.com/showthread.php?postid=759#post759
 
−
14.  http://forum.wolframscience.com/showthread.php?postid=764#post764
 
−
15.  http://forum.wolframscience.com/showthread.php?postid=766#post766
 
−
16.  http://forum.wolframscience.com/showthread.php?postid=767#post767
 
−
17.  http://forum.wolframscience.com/showthread.php?postid=773#post773
 
−
18.  http://forum.wolframscience.com/showthread.php?postid=775#post775
 
−
19.  http://forum.wolframscience.com/showthread.php?postid=777#post777
 
−
20.  http://forum.wolframscience.com/showthread.php?postid=791#post791
 
−
21.  http://forum.wolframscience.com/showthread.php?postid=1458#post1458
 
−
22.  http://forum.wolframscience.com/showthread.php?postid=1461#post1461
 
−
23.  http://forum.wolframscience.com/showthread.php?postid=1463#post1463
 
−
24.  http://forum.wolframscience.com/showthread.php?postid=1464#post1464
 
−
25.  http://forum.wolframscience.com/showthread.php?postid=1467#post1467
 
−
26.  http://forum.wolframscience.com/showthread.php?postid=1469#post1469
 
−
27.  http://forum.wolframscience.com/showthread.php?postid=1470#post1470
 
−
28.  http://forum.wolframscience.com/showthread.php?postid=1471#post1471
 
−
29.  http://forum.wolframscience.com/showthread.php?postid=1473#post1473
 
−
30.  http://forum.wolframscience.com/showthread.php?postid=1475#post1475
 
−
31.  http://forum.wolframscience.com/showthread.php?postid=1479#post1479
 
−
32.  http://forum.wolframscience.com/showthread.php?postid=1489#post1489
 
−
33.  http://forum.wolframscience.com/showthread.php?postid=1490#post1490
 
−
</pre>
 

Latest revision as of 15:30, 11 October 2013

Author: Jon Awbrey

The task ahead is to chart a course from general ideas about transformational equivalence classes of graphs to a notion of differential analytic turing automata (DATA). It may be a while before we get within sight of that goal, but it will provide a better measure of motivation to name the thread after the envisioned end rather than the more homely starting place.

The basic idea is as follows. One has a set \(\mathcal{G}\) of graphs and a set \(\mathcal{T}\) of transformation rules, and each rule \(\mathrm{t} \in \mathcal{T}\) has the effect of transforming graphs into graphs, \(\mathrm{t} : \mathcal{G} \to \mathcal{G}.\) In the cases that we shall be studying, this set of transformation rules partitions the set of graphs into transformational equivalence classes (TECs).

There are many interesting excursions to be had here, but I will focus mainly on logical applications, and and so the TECs I talk about will almost always have the character of logical equivalence classes (LECs).

An example that will figure heavily in the sequel is given by rooted trees as the species of graphs and a pair of equational transformation rules that derive from the graphical calculi of C.S. Peirce, as revived and extended by George Spencer Brown.

Here are the fundamental transformation rules, also referred to as the arithmetic axioms, more precisely, the arithmetic initials.

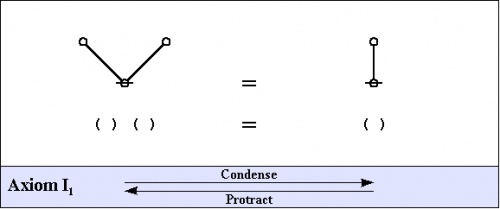PERS Figure 01.jpg (1)
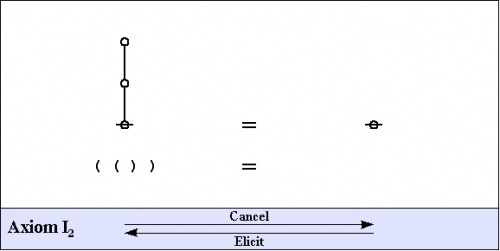PERS Figure 02.jpg (2)

That should be enough to get started.

Cactus Language

I will be making use of the cactus language extension of Peirce's Alpha Graphs, so called because it uses a species of graphs that are usually called "cacti" in graph theory. The last exposition of the cactus syntax that I've written can be found here:

The representational and computational efficiency of the cactus language for the tasks that are usually associated with boolean algebra and propositional calculus makes it possible to entertain a further extension, to what we may call differential logic, because it develops this basic level of logic in the same way that differential calculus augments analytic geometry to handle change and diversity. There are several different introductions to differential logic that I have written and distributed across the Internet. You might start with the following couple of treatments:

I will draw on those previously advertised resources of notation and theory as needed, but right now I sense the need for some concrete examples.

Example 1

Let's say we have a system that is known by the name of its state space \(X\!\) and we have a boolean state variable \(x : X \to \mathbb{B},\!\) where \(\mathbb{B} = \{ 0, 1 \}.\!\)

We observe \(X\!\) for a while, relative to a discrete time frame, and we write down the following sequence of values for \(x.\!\)

\(\begin{array}{c|c} t & x \'"`UNIQ-MathJax1-QINU`"' in other words'"`UNIQ-MathJax2-QINU`"' =='"`UNIQ--h-10--QINU`"'Notions of Approximation== {| cellpadding="2" cellspacing="2" width="100%" | width="60%" |   | width="40%" | for equalities are so weighed<br> that curiosity in neither can<br> make choice of either's moiety. |- | height="50px" |   | valign="top" | — ''King Lear'', Sc.1.5–7 (Quarto) |- |   | for qualities are so weighed<br> that curiosity in neither can<br> make choice of either's moiety.<br> |- | height="50px" |   | valign="top" | — ''King Lear'', 1.1.5–6 (Folio) |} Justifying a notion of approximation is a little more involved in general, and especially in these discrete logical spaces, than it would be expedient for people in a hurry to tangle with right now. I will just say that there are ''naive'' or ''obvious'' notions and there are ''sophisticated'' or ''subtle'' notions that we might choose among. The later would engage us in trying to construct proper logical analogues of Lie derivatives, and so let's save that for when we have become subtle or sophisticated or both. Against or toward that day, as you wish, let's begin with an option in plain view. Figure 1.4 illustrates one way of ranging over the cells of the underlying universe \(U^\bullet = [u, v]\!\) and selecting at each cell the linear proposition in \(\mathrm{d}U^\bullet = [\mathrm{d}u, \mathrm{d}v]\!\) that best approximates the patch of the difference map \({\mathrm{D}f}\!\) that is located there, yielding the following formula for the differential \(\mathrm{d}f.\!\)

\(\begin{array}{*{11}{c}} \mathrm{d}f & = & \mathrm{d}\texttt{((} u \texttt{)(} v \texttt{))} & = & uv \cdot 0 & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} \end{array}\) 

o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              / \     / \              |
|             /   \   /   \             |
|            /     \ /     \            |
|           o       o       o           |
|          / \     / \     / \          |
|         /   \   /   \   /   \         |
|        /     \ /     \ /     \        |
|       o       o       o       o       |
|      / \     /%\     /%\     / \      |
|     /   \   /%%%\   /%%%\   /   \     |
|    /     \ /%%%%%\ /%%%%%\ /     \    |
|   o       o%%%%%%%o%%%%%%%o       o   |
|   |\     /%\%%%%%/ \%%%%%/%\     /|   |
|   | \   /%%%\%%%/   \%%%/%%%\   / |   |
|   |  \ /%%%%%\%/     \%/%%%%%\ /  |   |
|   |   o%%%%%%%o       o%%%%%%%o   |   |
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
|   | u |  \%/%%%%%\ /%%%%%\%/  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 1.4.  df = linear approx to Df

Figure 2.4 illustrates one way of ranging over the cells of the underlying universe \(U^\bullet = [u, v]\!\) and selecting at each cell the linear proposition in \(\mathrm{d}U^\bullet = [du, dv]\!\) that best approximates the patch of the difference map \(\mathrm{D}g\!\) that is located there, yielding the following formula for the differential \(\mathrm{d}g.\!\)

\(\begin{array}{*{11}{c}} \mathrm{d}g & = & \mathrm{d}\texttt{((} u \texttt{,} v \texttt{))} & = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \end{array}\) 

o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              /%\     /%\              |
|             /%%%\   /%%%\             |
|            /%%%%%\ /%%%%%\            |
|           o%%%%%%%o%%%%%%%o           |
|          /%\%%%%%/ \%%%%%/%\          |
|         /%%%\%%%/   \%%%/%%%\         |
|        /%%%%%\%/     \%/%%%%%\        |
|       o%%%%%%%o       o%%%%%%%o       |
|      / \%%%%%/ \     / \%%%%%/ \      |
|     /   \%%%/   \   /   \%%%/   \     |
|    /     \%/     \ /     \%/     \    |
|   o       o       o       o       o   |
|   |\     /%\     / \     /%\     /|   |
|   | \   /%%%\   /   \   /%%%\   / |   |
|   |  \ /%%%%%\ /     \ /%%%%%\ /  |   |
|   |   o%%%%%%%o       o%%%%%%%o   |   |
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
|   | u |  \%/%%%%%\ /%%%%%\%/  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 2.4.  dg = linear approx to Dg

Well, \(g,\!\) that was easy, seeing as how \(\mathrm{D}g\!\) is already linear at each locus, \(\mathrm{d}g = \mathrm{D}g.\!\)

Analytic Series

We have been conducting the differential analysis of the logical transformation \(F : [u, v] \mapsto [u, v]\!\) defined as \(F : (u, v) \mapsto ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ ),\!\) and this means starting with the extended transformation \(\mathrm{E}F : [u, v, \mathrm{d}u, \mathrm{d}v] \to [u, v, \mathrm{d}u, \mathrm{d}v]\!\) and breaking it into an analytic series, \(\mathrm{E}F = F + \mathrm{d}F + \mathrm{d}^2 F + \ldots,\!\) and so on until there is nothing left to analyze any further.

As a general rule, one proceeds by way of the following stages:

\(\begin{array}{*{6}{l}} 1. & \mathrm{E}F & = & \mathrm{d}^0 F & + & \mathrm{r}^0 F \\ 2. & \mathrm{r}^0 F & = & \mathrm{d}^1 F & + & \mathrm{r}^1 F \\ 3. & \mathrm{r}^1 F & = & \mathrm{d}^2 F & + & \mathrm{r}^2 F \\ 4. & \ldots \end{array}\)

In our analysis of the transformation \(F,\!\) we carried out Step 1 in the more familiar form \(\mathrm{E}F = F + \mathrm{D}F\!\) and we have just reached Step 2 in the form \(\mathrm{D}F = \mathrm{d}F + \mathrm{r}F,\!\) where \(\mathrm{r}F\!\) is the residual term that remains for us to examine next.

Note. I'm am trying to give quick overview here, and this forces me to omit many picky details. The picky reader may wish to consult the more detailed presentation of this material at the following locations:

Let's push on with the analysis of the transformation:

\(\begin{matrix} F & : & (u, v) & \mapsto & (f(u, v), g(u, v)) & = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~) \end{matrix}\)

For ease of comparison and computation, I will collect the Figures that we need for the remainder of the work together on one page.

Computation Summary for Logical Disjunction

Figure 1.1 shows the expansion of \(f = \texttt{((} u \texttt{)(} v \texttt{))}\!\) over \([u, v]\!\) to produce the expression:

\(\begin{matrix} uv & + & u \texttt{(} v \texttt{)} & + & \texttt{(} u \texttt{)} v \end{matrix}\)

Figure 1.2 shows the expansion of \(\mathrm{E}f = \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}\!\) over \([u, v]\!\) to produce the expression:

\(\begin{matrix} uv \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \end{matrix}\)

In general, \(\mathrm{E}f\!\) tells you what you would have to do, from wherever you are in the universe \([u, v],\!\) if you want to end up in a place where \(f\!\) is true. In this case, where the prevailing proposition \(f\!\) is \(\texttt{((} u \texttt{)(} v \texttt{))},\!\) the indication \(uv \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)}\!\) of \(\mathrm{E}f\!\) tells you this: If \(u\!\) and \(v\!\) are both true where you are, then just don't change both \(u\!\) and \(v\!\) at once, and you will end up in a place where \(\texttt{((} u \texttt{)(} v \texttt{))}\!\) is true.

Figure 1.3 shows the expansion of \(\mathrm{D}f\) over \([u, v]\!\) to produce the expression:

\(\begin{matrix} uv \cdot \mathrm{d}u ~ \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \end{matrix}\)

In general, \({\mathrm{D}f}\!\) tells you what you would have to do, from wherever you are in the universe \([u, v],\!\) if you want to bring about a change in the value of \(f,\!\) that is, if you want to get to a place where the value of \(f\!\) is different from what it is where you are. In the present case, where the reigning proposition \(f\!\) is \(\texttt{((} u \texttt{)(} v \texttt{))},\!\) the term \(uv \cdot \mathrm{d}u ~ \mathrm{d}v\!\) of \({\mathrm{D}f}\!\) tells you this: If \(u\!\) and \(v\!\) are both true where you are, then you would have to change both \(u\!\) and \(v\!\) in order to reach a place where the value of \(f\!\) is different from what it is where you are.

Figure 1.4 approximates \({\mathrm{D}f}\!\) by the linear form \(\mathrm{d}f\!\) that expands over \([u, v]\!\) as follows:

\(\begin{matrix} \mathrm{d}f & = & uv \cdot 0 & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} \'"`UNIQ-MathJax3-QINU`"' Another way to convey the same information is by means of the extended proposition'"`UNIQ-MathJax4-QINU`"' {| align="center" cellpadding="8" style="text-align:center" | \(\text{Orbit 2}\!\)

\(\begin{array}{c|cc|cc|cc|} t & u & v & \mathrm{d}u & \mathrm{d}v & \mathrm{d}^2 u & \mathrm{d}^2 v \\[8pt] 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 & 1 & 1 & 1 \\ 2 & 1 & 0 & 0 & 0 & 0 & 0 \\ 3 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel \end{array}\)

A more fine combing of the second Table brings to mind a rule that partly covers the remaining cases, that is, \(\mathrm{d}u = v, ~ \mathrm{d}v = \texttt{(} u \texttt{)}.\!\) This much information about Orbit 2 is also encapsulated by the extended proposition \(\texttt{(} uv \texttt{)((} \mathrm{d}u \texttt{,} v \texttt{))(} \mathrm{d}v, u \texttt{)},\!\) which says that \(u\!\) and \(v\!\) are not both true at the same time, while \(\mathrm{d}u\!\) is equal in value to \(v\!\) and \(\mathrm{d}v\!\) is opposite in value to \(u.\!\)

Turing Machine Example

☞ See Theme One Program for documentation of the cactus graph syntax and the propositional modeling program used below.

By way of providing a simple illustration of Cook's Theorem, namely, that “Propositional Satisfiability is NP-Complete”, I will describe one way to translate finite approximations of turing machines into propositional expressions, using the cactus language syntax for propositional calculus that I will describe in more detail as we proceed.

\(\mathrm{Stilt}(k) =\!\)
Space and time limited turing machine,
with \(k\!\) units of space and \(k\!\) units of time.
\(\mathrm{Stunt}(k) =\!\)
Space and time limited turing machine,
for computing the parity of a bit string, with number of tape cells of input equal to \(k.\!\)

I will follow the pattern of discussion in Herbert Wilf (1986), Algorithms and Complexity, pp. 188–201, but translate his logical formalism into cactus language, which is more efficient in regard to the number of propositional clauses that are required.

A turing machine for computing the parity of a bit string is described by means of the following Figure and Table.

Parity Machine.jpg
\(\text{Figure 3.} ~~ \text{Parity Machine}\!\) 


Table 4.  Parity Machine
o-------o--------o-------------o---------o------------o
| State | Symbol | Next Symbol | Ratchet | Next State |
|   Q   |   S    |     S'      |   dR    |     Q'     |
o-------o--------o-------------o---------o------------o
|   0   |   0    |     0       |   +1    |     0      |
|   0   |   1    |     1       |   +1    |     1      |
|   0   |   #    |     #       |   -1    |     #      |
|   1   |   0    |     0       |   +1    |     1      |
|   1   |   1    |     1       |   +1    |     0      |
|   1   |   #    |     #       |   -1    |     *      |
o-------o--------o-------------o---------o------------o


The TM has a finite automaton (FA) as one component. Let us refer to this particular FA by the name of \(\mathrm{M}.\)

The tape head (that is, the read unit) will be called \(\mathrm{H}.\) The registers are also called tape cells or tape squares.

Finite Approximations

To see how each finite approximation to a given turing machine can be given a purely propositional description, one fixes the parameter \(k\!\) and limits the rest of the discussion to describing \(\mathrm{Stilt}(k),\!\) which is not really a full-fledged TM anymore but just a finite automaton in disguise.

In this example, for the sake of a minimal illustration, we choose \(k = 2,\!\) and discuss \(\mathrm{Stunt}(2).\) Since the zeroth tape cell and the last tape cell are both occupied by the character \(^{\backprime\backprime}\texttt{\#}^{\prime\prime}\) that is used for both the beginning of file \((\mathrm{bof})\) and the end of file \((\mathrm{eof})\) markers, this allows for only one digit of significant computation.

To translate \(\mathrm{Stunt}(2)\) into propositional form we use the following collection of basic propositions, boolean variables, or logical features, depending on what one prefers to call them:

The basic propositions for describing the present state function \(\mathrm{QF} : P \to Q\) are these:

\(\begin{matrix} \texttt{p0\_q\#}, & \texttt{p0\_q*}, & \texttt{p0\_q0}, & \texttt{p0\_q1}, \\[6pt] \texttt{p1\_q\#}, & \texttt{p1\_q*}, & \texttt{p1\_q0}, & \texttt{p1\_q1}, \\[6pt] \texttt{p2\_q\#}, & \texttt{p2\_q*}, & \texttt{p2\_q0}, & \texttt{p2\_q1}, \\[6pt] \texttt{p3\_q\#}, & \texttt{p3\_q*}, & \texttt{p3\_q0}, & \texttt{p3\_q1}. \end{matrix}\)

The proposition of the form \(\texttt{pi\_qj}\) says:

At the point-in-time \(p_i,\!\) the finite state machine \(\mathrm{M}\) is in the state \(q_j.\!\)

The basic propositions for describing the present register function \(\mathrm{RF} : P \to R\) are these:

\(\begin{matrix} \texttt{p0\_r0}, & \texttt{p0\_r1}, & \texttt{p0\_r2}, & \texttt{p0\_r3}, \\[6pt] \texttt{p1\_r0}, & \texttt{p1\_r1}, & \texttt{p1\_r2}, & \texttt{p1\_r3}, \\[6pt] \texttt{p2\_r0}, & \texttt{p2\_r1}, & \texttt{p2\_r2}, & \texttt{p2\_r3}, \\[6pt] \texttt{p3\_r0}, & \texttt{p3\_r1}, & \texttt{p3\_r2}, & \texttt{p3\_r3}. \end{matrix}\)

The proposition of the form \(\texttt{pi\_rj}\) says:

At the point-in-time \(p_i,\!\) the tape head \(\mathrm{H}\) is on the tape cell \(r_j.\!\)

The basic propositions for describing the present symbol function \(\mathrm{SF} : P \to (R \to S)\) are these:

\(\begin{matrix} \texttt{p0\_r0\_s\#}, & \texttt{p0\_r0\_s*}, & \texttt{p0\_r0\_s0}, & \texttt{p0\_r0\_s1}, \\[4pt] \texttt{p0\_r1\_s\#}, & \texttt{p0\_r1\_s*}, & \texttt{p0\_r1\_s0}, & \texttt{p0\_r1\_s1}, \\[4pt] \texttt{p0\_r2\_s\#}, & \texttt{p0\_r2\_s*}, & \texttt{p0\_r2\_s0}, & \texttt{p0\_r2\_s1}, \\[4pt] \texttt{p0\_r3\_s\#}, & \texttt{p0\_r3\_s*}, & \texttt{p0\_r3\_s0}, & \texttt{p0\_r3\_s1}, \\[12pt] \texttt{p1\_r0\_s\#}, & \texttt{p1\_r0\_s*}, & \texttt{p1\_r0\_s0}, & \texttt{p1\_r0\_s1}, \\[4pt] \texttt{p1\_r1\_s\#}, & \texttt{p1\_r1\_s*}, & \texttt{p1\_r1\_s0}, & \texttt{p1\_r1\_s1}, \\[4pt] \texttt{p1\_r2\_s\#}, & \texttt{p1\_r2\_s*}, & \texttt{p1\_r2\_s0}, & \texttt{p1\_r2\_s1}, \\[4pt] \texttt{p1\_r3\_s\#}, & \texttt{p1\_r3\_s*}, & \texttt{p1\_r3\_s0}, & \texttt{p1\_r3\_s1}, \\[12pt] \texttt{p2\_r0\_s\#}, & \texttt{p2\_r0\_s*}, & \texttt{p2\_r0\_s0}, & \texttt{p2\_r0\_s1}, \\[4pt] \texttt{p2\_r1\_s\#}, & \texttt{p2\_r1\_s*}, & \texttt{p2\_r1\_s0}, & \texttt{p2\_r1\_s1}, \\[4pt] \texttt{p2\_r2\_s\#}, & \texttt{p2\_r2\_s*}, & \texttt{p2\_r2\_s0}, & \texttt{p2\_r2\_s1}, \\[4pt] \texttt{p2\_r3\_s\#}, & \texttt{p2\_r3\_s*}, & \texttt{p2\_r3\_s0}, & \texttt{p2\_r3\_s1}, \\[12pt] \texttt{p3\_r0\_s\#}, & \texttt{p3\_r0\_s*}, & \texttt{p3\_r0\_s0}, & \texttt{p3\_r0\_s1}, \\[4pt] \texttt{p3\_r1\_s\#}, & \texttt{p3\_r1\_s*}, & \texttt{p3\_r1\_s0}, & \texttt{p3\_r1\_s1}, \\[4pt] \texttt{p3\_r2\_s\#}, & \texttt{p3\_r2\_s*}, & \texttt{p3\_r2\_s0}, & \texttt{p3\_r2\_s1}, \\[4pt] \texttt{p3\_r3\_s\#}, & \texttt{p3\_r3\_s*}, & \texttt{p3\_r3\_s0}, & \texttt{p3\_r3\_s1}. \end{matrix}\)

The proposition of the form \(\texttt{pi\_rj\_sk}\) says:

At the point-in-time \(p_i,\!\) the tape cell \(r_j\!\) bears the mark \(s_k.\!\)

Initial Conditions

Given but a single free square on the tape, there are just two different sets of initial conditions for \(\mathrm{Stunt}(2),\) the finite approximation to the parity turing machine that we are presently considering.

Initial Conditions for Tape Input "0"

The following conjunction of 5 basic propositions describes the initial conditions when \(\mathrm{Stunt}(2)\) is started with an input of "0" in its free square:

\(\begin{array}{l} \texttt{p0\_q0} \\ \\ \texttt{p0\_r1} \\ \\ \texttt{p0\_r0\_s\#} \\ \texttt{p0\_r1\_s0} \\ \texttt{p0\_r2\_s\#} \end{array}\)

This conjunction of basic propositions may be read as follows:

At time \(p_0,\!\) machine \(\mathrm{M}\) is in the state \(q_0,\!\)

At time \(p_0,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\)

At time \(p_0,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\)

At time \(p_0,\!\) cell \(r_1\!\) contains the symbol \(\texttt{0},\)

At time \(p_0,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#}.\)

Initial Conditions for Tape Input "1"

The following conjunction of 5 basic propositions describes the initial conditions when \(\mathrm{Stunt}(2)\) is started with an input of "1" in its free square:

\(\begin{array}{l} \texttt{p0\_q0} \\ \\ \texttt{p0\_r1} \\ \\ \texttt{p0\_r0\_s\#} \\ \texttt{p0\_r1\_s1} \\ \texttt{p0\_r2\_s\#} \end{array}\)

This conjunction of basic propositions may be read as follows:

At time \(p_0,\!\) machine \(\mathrm{M}\) is in the state \(q_0,\!\)

At time \(p_0,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\)

At time \(p_0,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\)

At time \(p_0,\!\) cell \(r_1\!\) contains the symbol \(\texttt{1},\)

At time \(p_0,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#}.\)

Propositional Program

A complete description of \(\mathrm{Stunt}(2)\) in propositional form is obtained by conjoining one of the above choices for initial conditions with all of the following sets of propositions, that serve in effect as a simple type of declarative program, telling us all that we need to know about the anatomy and behavior of the truncated TM in question.

Mediate Conditions

\(\begin{array}{l} \texttt{(~p0\_q\#~(~p1\_q\#~))} \\ \texttt{(~p0\_q*~(~p1\_q*~))} \\ \\ \texttt{(~p1\_q\#~(~p2\_q\#~))} \\ \texttt{(~p1\_q*~(~p2\_q*~))} \end{array}\)

Terminal Conditions

\(\begin{array}{l} \texttt{((~p2\_q\#~)(~p2\_q*~))} \end{array}\)

State Partition

\(\begin{array}{l} \texttt{((~p0\_q0~),(~p0\_q1~),(~p0\_q\#~),(~p0\_q*~))} \\ \texttt{((~p1\_q0~),(~p1\_q1~),(~p1\_q\#~),(~p1\_q*~))} \\ \texttt{((~p2\_q0~),(~p2\_q1~),(~p2\_q\#~),(~p2\_q*~))} \end{array}\)

Register Partition

\(\begin{array}{l} \texttt{((~p0\_r0~),(~p0\_r1~),(~p0\_r2~))} \\ \texttt{((~p1\_r0~),(~p1\_r1~),(~p1\_r2~))} \\ \texttt{((~p2\_r0~),(~p2\_r1~),(~p2\_r2~))} \end{array}\)

Symbol Partition

\(\begin{array}{l} \texttt{((~p0\_r0\_s0~),(~p0\_r0\_s1~),(~p0\_r0\_s\#~))} \\ \texttt{((~p0\_r1\_s0~),(~p0\_r1\_s1~),(~p0\_r1\_s\#~))} \\ \texttt{((~p0\_r2\_s0~),(~p0\_r2\_s1~),(~p0\_r2\_s\#~))} \\ \\ \texttt{((~p1\_r0\_s0~),(~p1\_r0\_s1~),(~p1\_r0\_s\#~))} \\ \texttt{((~p1\_r1\_s0~),(~p1\_r1\_s1~),(~p1\_r1\_s\#~))} \\ \texttt{((~p1\_r2\_s0~),(~p1\_r2\_s1~),(~p1\_r2\_s\#~))} \\ \\ \texttt{((~p2\_r0\_s0~),(~p2\_r0\_s1~),(~p2\_r0\_s\#~))} \\ \texttt{((~p2\_r1\_s0~),(~p2\_r1\_s1~),(~p2\_r1\_s\#~))} \\ \texttt{((~p2\_r2\_s0~),(~p2\_r2\_s1~),(~p2\_r2\_s\#~))} \end{array}\)

Interaction Conditions

\(\begin{array}{l} \texttt{((~p0\_r0~) ~p0\_r0\_s0~ (~p1\_r0\_s0~))} \\ \texttt{((~p0\_r0~) ~p0\_r0\_s1~ (~p1\_r0\_s1~))} \\ \texttt{((~p0\_r0~) ~p0\_r0\_s\#~ (~p1\_r0\_s\#~))} \\ \\ \texttt{((~p0\_r1~) ~p0\_r1\_s0~ (~p1\_r1\_s0~))} \\ \texttt{((~p0\_r1~) ~p0\_r1\_s1~ (~p1\_r1\_s1~))} \\ \texttt{((~p0\_r1~) ~p0\_r1\_s\#~ (~p1\_r1\_s\#~))} \\ \\ \texttt{((~p0\_r2~) ~p0\_r2\_s0~ (~p1\_r2\_s0~))} \\ \texttt{((~p0\_r2~) ~p0\_r2\_s1~ (~p1\_r2\_s1~))} \\ \texttt{((~p0\_r2~) ~p0\_r2\_s\#~ (~p1\_r2\_s\#~))} \\ \\ \texttt{((~p1\_r0~) ~p1\_r0\_s0~ (~p2\_r0\_s0~))} \\ \texttt{((~p1\_r0~) ~p1\_r0\_s1~ (~p2\_r0\_s1~))} \\ \texttt{((~p1\_r0~) ~p1\_r0\_s\#~ (~p2\_r0\_s\#~))} \\ \\ \texttt{((~p1\_r1~) ~p1\_r1\_s0~ (~p2\_r1\_s0~))} \\ \texttt{((~p1\_r1~) ~p1\_r1\_s1~ (~p2\_r1\_s1~))} \\ \texttt{((~p1\_r1~) ~p1\_r1\_s\#~ (~p2\_r1\_s\#~))} \\ \\ \texttt{((~p1\_r2~) ~p1\_r2\_s0~ (~p2\_r2\_s0~))} \\ \texttt{((~p1\_r2~) ~p1\_r2\_s1~ (~p2\_r2\_s1~))} \\ \texttt{((~p1\_r2~) ~p1\_r2\_s\#~ (~p2\_r2\_s\#~))} \end{array}\)

Transition Relations

\(\begin{array}{l} \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s0~~(~p1\_q0~~p1\_r2~~p1\_r1\_s0~))} \\ \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s1~~(~p1\_q1~~p1\_r2~~p1\_r1\_s1~))} \\ \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q\#~~p1\_r0~~p1\_r1\_s\#~))} \\ \texttt{(~p0\_q0~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q\#~~p1\_r1~~p1\_r2\_s\#~))} \\ \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s0~~(~p1\_q1~~p1\_r2~~p1\_r1\_s0~))} \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s1~~(~p1\_q0~~p1\_r2~~p1\_r1\_s1~))} \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q*~~p1\_r0~~p1\_r1\_s\#~))} \\ \texttt{(~p0\_q1~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q*~~p1\_r1~~p1\_r2\_s\#~))} \\ \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s0~~(~p2\_q0~~p2\_r2~~p2\_r1\_s0~))} \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s1~~(~p2\_q1~~p2\_r2~~p2\_r1\_s1~))} \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q\#~~p2\_r0~~p2\_r1\_s\#~))} \\ \texttt{(~p1\_q0~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q\#~~p2\_r1~~p2\_r2\_s\#~))} \\ \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s0~~(~p2\_q1~~p2\_r2~~p2\_r1\_s0~))} \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s1~~(~p2\_q0~~p2\_r2~~p2\_r1\_s1~))} \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q*~~p2\_r0~~p2\_r1\_s\#~))} \\ \texttt{(~p1\_q1~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q*~~p2\_r1~~p2\_r2\_s\#~))} \end{array}\)

Interpretation of the Propositional Program

Let us now run through the propositional specification of \(\mathrm{Stunt}(2),\) our truncated TM, and paraphrase what it says in ordinary language.

Mediate Conditions

\(\begin{array}{l} \texttt{(~p0\_q\#~(~p1\_q\#~))} \\ \texttt{(~p0\_q*~(~p1\_q*~))} \\ \\ \texttt{(~p1\_q\#~(~p2\_q\#~))} \\ \texttt{(~p1\_q*~(~p2\_q*~))} \end{array}\)

In the interpretation of the cactus language for propositional logic that we are using here, an expression of the form \(\texttt{(p(q))}\) expresses a conditional, an implication, or an if-then proposition, commonly read in one of the following ways:

\(\begin{array}{l} \mathrm{not}~ p ~\mathrm{without}~ q \\[4pt] p ~\mathrm{implies}~ q \\[4pt] \mathrm{if}~ p ~\mathrm{then}~ q \\[4pt] p \Rightarrow q \end{array}\)

A text string expression of the form \(\texttt{(p(q))}\) corresponds to a graph-theoretic data-structure of the following form: 


o---------------------------------------o
|                                       |
|                 p   q                 |
|                 o---o                 |
|                 |                     |
|                 @                     |
|                                       |
o---------------------------------------o
|               ( p ( q ))              |
o---------------------------------------o


Taken together, the Mediate Conditions state the following:

If \(\mathrm{M}\) at \(p_0\!\) is in state \(q_\#,\!\) then \(\mathrm{M}\) at \(p_1\!\) is in state \(q_\#,\!\) and

If \(\mathrm{M}\) at \(p_0\!\) is in state \(q_*,\!\) then \(\mathrm{M}\) at \(p_1\!\) is in state \(q_*,\!\) and

If \(\mathrm{M}\) at \(p_1\!\) is in state \(q_\#,\!\) then \(\mathrm{M}\) at \(p_2\!\) is in state \(q_\#,\!\) and

If \(\mathrm{M}\) at \(p_1\!\) is in state \(q_*,\!\) then \(\mathrm{M}\) at \(p_2\!\) is in state \(q_*.\!\)

Terminal Conditions

\(\begin{array}{l} \texttt{((~p2\_q\#~)(~p2\_q*~))} \end{array}\)

In cactus syntax, an expression of the form \(\texttt{((p)(q))}\) expresses the disjunction \(p ~\mathrm{or}~ q.\) The corresponding cactus graph, here just a tree, has the following shape: 


o---------------------------------------o
|                                       |
|                 p   q                 |
|                 o   o                 |
|                  \ /                  |
|                   o                   |
|                   |                   |
|                   @                   |
|                                       |
o---------------------------------------o
|               ((p) (q))               |
o---------------------------------------o


In effect, the Terminal Conditions state the following:

At time \(p_2\!\) machine \(\mathrm{M}\) is in state \(q_\#,\!\) or

At time \(p_2\!\) machine \(\mathrm{M}\) is in state \(q_*.\!\)

State Partition

\(\begin{array}{l} \texttt{((~p0\_q0~),(~p0\_q1~),(~p0\_q\#~),(~p0\_q*~))} \\ \texttt{((~p1\_q0~),(~p1\_q1~),(~p1\_q\#~),(~p1\_q*~))} \\ \texttt{((~p2\_q0~),(~p2\_q1~),(~p2\_q\#~),(~p2\_q*~))} \end{array}\)

In cactus syntax, an expression of the form \(\texttt{((} e_1 \texttt{),(} e_2 \texttt{),(} \ldots \texttt{),(} e_k \texttt{))}\!\) expresses a statement to the effect that exactly one of the expressions \(e_j\!\) is true, for \(j = 1 ~\mathit{to}~ k.\) Expressions of this form are called universal partition expressions, and the corresponding painted and rooted cactus (PARC) has the following shape: 


o---------------------------------------o
|                                       |
|         e_1   e_2   ...   e_k         |
|          o     o           o          |
|          |     |           |          |
|          o-----o--- ... ---o          |
|           \               /           |
|            \             /            |
|             \           /             |
|              \         /              |
|               \       /               |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   @                   |
|                                       |
o---------------------------------------o
|       ((e_1),(e_2),(...),(e_k))       |
o---------------------------------------o


The State Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction expressing the condition that \(\mathrm{M}\) has to be in one and only one of its states at each point in time under consideration. In short, we have the constraint:

At each of the points in time \(p_i,\!\) for \(i\!\) in the set \(\{ 0, 1, 2 \},\!\)

\(\mathrm{M}\) can be in exactly one state \(q_j,\!\) for \(j\!\) in the set \(\{ 0, 1, \#, * \}.\!\)

Register Partition

\(\begin{array}{l} \texttt{((~p0\_r0~),(~p0\_r1~),(~p0\_r2~))} \\ \texttt{((~p1\_r0~),(~p1\_r1~),(~p1\_r2~))} \\ \texttt{((~p2\_r0~),(~p2\_r1~),(~p2\_r2~))} \end{array}\)

The Register Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction saying that the read head \(\mathrm{H}\) must be reading one and only one of the registers or tape cells available to it at each of the points in time under consideration. In sum:

At each of the points in time \(p_i,\!\) for \(i = 0, 1, 2,\!\)

\(\mathrm{H}\) is reading exactly one cell \(r_j,\!\) for \(j = 0, 1, 2.\!\)

Symbol Partition

\(\begin{array}{l} \texttt{((~p0\_r0\_s0~),(~p0\_r0\_s1~),(~p0\_r0\_s\#~))} \\ \texttt{((~p0\_r1\_s0~),(~p0\_r1\_s1~),(~p0\_r1\_s\#~))} \\ \texttt{((~p0\_r2\_s0~),(~p0\_r2\_s1~),(~p0\_r2\_s\#~))} \\ \\ \texttt{((~p1\_r0\_s0~),(~p1\_r0\_s1~),(~p1\_r0\_s\#~))} \\ \texttt{((~p1\_r1\_s0~),(~p1\_r1\_s1~),(~p1\_r1\_s\#~))} \\ \texttt{((~p1\_r2\_s0~),(~p1\_r2\_s1~),(~p1\_r2\_s\#~))} \\ \\ \texttt{((~p2\_r0\_s0~),(~p2\_r0\_s1~),(~p2\_r0\_s\#~))} \\ \texttt{((~p2\_r1\_s0~),(~p2\_r1\_s1~),(~p2\_r1\_s\#~))} \\ \texttt{((~p2\_r2\_s0~),(~p2\_r2\_s1~),(~p2\_r2\_s\#~))} \end{array}\)

The Symbol Partition segment of the propositional program for \(\mathrm{Stunt}(2)\) consists of nine universal partition expressions, taken in conjunction stipulating that there has to be one and only one symbol in each of the registers at each point in time under consideration. In short, we have:

At each of the points in time \(p_i,\!\) for \(i\!\) in \(\{ 0, 1, 2 \},\!\)

in each of the tape registers \(r_j,\!\) for \(j\!\) in \(\{ 0, 1, 2 \},\!\)

there can be exactly one sign \(s_k,\!\) for \(k\!\) in \(\{ 0, 1, \# \}.\!\)

Interaction Conditions

\(\begin{array}{l} \texttt{((~p0\_r0~) ~p0\_r0\_s0~ (~p1\_r0\_s0~))} \\ \texttt{((~p0\_r0~) ~p0\_r0\_s1~ (~p1\_r0\_s1~))} \\ \texttt{((~p0\_r0~) ~p0\_r0\_s\#~ (~p1\_r0\_s\#~))} \\ \\ \texttt{((~p0\_r1~) ~p0\_r1\_s0~ (~p1\_r1\_s0~))} \\ \texttt{((~p0\_r1~) ~p0\_r1\_s1~ (~p1\_r1\_s1~))} \\ \texttt{((~p0\_r1~) ~p0\_r1\_s\#~ (~p1\_r1\_s\#~))} \\ \\ \texttt{((~p0\_r2~) ~p0\_r2\_s0~ (~p1\_r2\_s0~))} \\ \texttt{((~p0\_r2~) ~p0\_r2\_s1~ (~p1\_r2\_s1~))} \\ \texttt{((~p0\_r2~) ~p0\_r2\_s\#~ (~p1\_r2\_s\#~))} \\ \\ \texttt{((~p1\_r0~) ~p1\_r0\_s0~ (~p2\_r0\_s0~))} \\ \texttt{((~p1\_r0~) ~p1\_r0\_s1~ (~p2\_r0\_s1~))} \\ \texttt{((~p1\_r0~) ~p1\_r0\_s\#~ (~p2\_r0\_s\#~))} \\ \\ \texttt{((~p1\_r1~) ~p1\_r1\_s0~ (~p2\_r1\_s0~))} \\ \texttt{((~p1\_r1~) ~p1\_r1\_s1~ (~p2\_r1\_s1~))} \\ \texttt{((~p1\_r1~) ~p1\_r1\_s\#~ (~p2\_r1\_s\#~))} \\ \\ \texttt{((~p1\_r2~) ~p1\_r2\_s0~ (~p2\_r2\_s0~))} \\ \texttt{((~p1\_r2~) ~p1\_r2\_s1~ (~p2\_r2\_s1~))} \\ \texttt{((~p1\_r2~) ~p1\_r2\_s\#~ (~p2\_r2\_s\#~))} \end{array}\)

In briefest terms, the Interaction Conditions simply express the circumstance that the mark on a tape cell cannot change between two points in time unless the tape head is over the cell in question at the initial one of those points in time. All that we have to do is to see how they manage to say this.

Consider a cactus expression of the following form:

\(\begin{array}{l} \texttt{((}~ p_i\_r_j ~\texttt{)}~ p_i\_r_j\_s_k ~\texttt{(}~ p_{i+1}\_r_j\_s_k ~\texttt{))} \end{array}\)

This expression has the corresponding cactus graph: 

o---------------------------------------o
|                                       |
|         p<i>_r<j>   p<i+1>_r<j>_s<k>  |
|                 o   o                 |
|                  \ /                  |
|    p<i>_r<j>_s<k> o                   |
|                   |                   |
|                   @                   |
|                                       |
o---------------------------------------o

A propositional expression of this form can be read as follows:

\(\mathrm{If}\)
At the time \(p_i,\!\) the tape cell \(r_j\!\) bears the mark \(s_k,\!\)
\(\mathrm{But}\) it is not the case that:
At the time \(p_i,\!\) the tape head is on the tape cell \(r_j,\!\)
\(\mathrm{Then}\)
At the time \(p_{i+1},\!\) the tape cell \(r_j\!\) bears the mark \(s_k.\!\)

The eighteen clauses of the Interaction Conditions simply impose one such constraint on symbol changes for each combination of the times \(p_0, p_1,\!\) registers \(r_0, r_1, r_2,\!\) and symbols \(s_0, s_1, s_\#.\!\)

Transition Relations

\(\begin{array}{l} \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s0~~(~p1\_q0~~p1\_r2~~p1\_r1\_s0~))} \\ \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s1~~(~p1\_q1~~p1\_r2~~p1\_r1\_s1~))} \\ \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q\#~~p1\_r0~~p1\_r1\_s\#~))} \\ \texttt{(~p0\_q0~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q\#~~p1\_r1~~p1\_r2\_s\#~))} \\ \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s0~~(~p1\_q1~~p1\_r2~~p1\_r1\_s0~))} \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s1~~(~p1\_q0~~p1\_r2~~p1\_r1\_s1~))} \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q*~~p1\_r0~~p1\_r1\_s\#~))} \\ \texttt{(~p0\_q1~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q*~~p1\_r1~~p1\_r2\_s\#~))} \\ \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s0~~(~p2\_q0~~p2\_r2~~p2\_r1\_s0~))} \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s1~~(~p2\_q1~~p2\_r2~~p2\_r1\_s1~))} \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q\#~~p2\_r0~~p2\_r1\_s\#~))} \\ \texttt{(~p1\_q0~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q\#~~p2\_r1~~p2\_r2\_s\#~))} \\ \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s0~~(~p2\_q1~~p2\_r2~~p2\_r1\_s0~))} \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s1~~(~p2\_q0~~p2\_r2~~p2\_r1\_s1~))} \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q*~~p2\_r0~~p2\_r1\_s\#~))} \\ \texttt{(~p1\_q1~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q*~~p2\_r1~~p2\_r2\_s\#~))} \end{array}\)

The Transition Relation segment of the propositional program for \(\mathrm{Stunt}(2)\) consists of sixteen implication statements with complex antecedents and consequents. Taken together, these give propositional expression to the TM Figure and Table that were given at the outset.

Just by way of a single example, consider the clause:

\(\texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s1~~(~p1\_q1~~p1\_r2~~p1\_r1\_s1~))}\)

This complex implication statement can be read to say:

\(\mathrm{If}\)
At the time \(p_0,\!\) the machine \(\mathrm{M}\) is in the state \(q_0,\!\) and
At the time \(p_0,\!\) the scanner \(\mathrm{H}\) is reading cell \(r_1,\!\) and
At the time \(p_0,\!\) the tape cell \(r_1\!\) contains a \(\texttt{1},\)
\(\mathrm{Then}\)
At the time \(p_1,\!\) the machine \(\mathrm{M}\) is in the state \(q_1,\!\) and
At the time \(p_1,\!\) the scanner \(\mathrm{H}\) is reading cell \(r_2,\!\) and
At the time \(p_1,\!\) the tape cell \(r_1\!\) contains a \(\texttt{1}.\)

Computation

The propositional program for \(\mathrm{Stunt}(2)\) uses the following set of \(9 + 12 + 36 = 57\!\) basic propositions or boolean variables:

\(\begin{matrix} \texttt{p0\_r0}, & \texttt{p0\_r1}, & \texttt{p0\_r2}, \\[6pt] \texttt{p1\_r0}, & \texttt{p1\_r1}, & \texttt{p1\_r2}, \\[6pt] \texttt{p2\_r0}, & \texttt{p2\_r1}, & \texttt{p2\_r2}. \end{matrix}\)

\(\begin{matrix} \texttt{p0\_q\#}, & \texttt{p0\_q*}, & \texttt{p0\_q0}, & \texttt{p0\_q1}, \\[6pt] \texttt{p1\_q\#}, & \texttt{p1\_q*}, & \texttt{p1\_q0}, & \texttt{p1\_q1}, \\[6pt] \texttt{p2\_q\#}, & \texttt{p2\_q*}, & \texttt{p2\_q0}, & \texttt{p2\_q1}. \end{matrix}\)

\(\begin{matrix} \texttt{p0\_r0\_s\#}, & \texttt{p0\_r0\_s*}, & \texttt{p0\_r0\_s0}, & \texttt{p0\_r0\_s1}, \\[4pt] \texttt{p0\_r1\_s\#}, & \texttt{p0\_r1\_s*}, & \texttt{p0\_r1\_s0}, & \texttt{p0\_r1\_s1}, \\[4pt] \texttt{p0\_r2\_s\#}, & \texttt{p0\_r2\_s*}, & \texttt{p0\_r2\_s0}, & \texttt{p0\_r2\_s1}, \\[12pt] \texttt{p1\_r0\_s\#}, & \texttt{p1\_r0\_s*}, & \texttt{p1\_r0\_s0}, & \texttt{p1\_r0\_s1}, \\[4pt] \texttt{p1\_r1\_s\#}, & \texttt{p1\_r1\_s*}, & \texttt{p1\_r1\_s0}, & \texttt{p1\_r1\_s1}, \\[4pt] \texttt{p1\_r2\_s\#}, & \texttt{p1\_r2\_s*}, & \texttt{p1\_r2\_s0}, & \texttt{p1\_r2\_s1}, \\[12pt] \texttt{p2\_r0\_s\#}, & \texttt{p2\_r0\_s*}, & \texttt{p2\_r0\_s0}, & \texttt{p2\_r0\_s1}, \\[4pt] \texttt{p2\_r1\_s\#}, & \texttt{p2\_r1\_s*}, & \texttt{p2\_r1\_s0}, & \texttt{p2\_r1\_s1}, \\[4pt] \texttt{p2\_r2\_s\#}, & \texttt{p2\_r2\_s*}, & \texttt{p2\_r2\_s0}, & \texttt{p2\_r2\_s1}. \end{matrix}\)

This means that the propositional program itself is nothing but a single proposition or boolean function of the form \(p : \mathbb{B}^{57} \to \mathbb{B}.\)

An assignment of boolean values to the above set of boolean variables is called an interpretation of the proposition \(p,\!\) and any interpretation of \(p\!\) that makes the proposition \(p : \mathbb{B}^{57} \to \mathbb{B}\) evaluate to \(1\!\) is referred to as a satisfying interpretation of the proposition \(p.\!\) Another way to specify interpretations, instead of giving them as bit vectors in \(\mathbb{B}^{57}\) and trying to remember some arbitrary ordering of variables, is to give them in the form of singular propositions, that is, a conjunction of the form \(e_1 \cdot \ldots \cdot e_{57}\) where each \(e_j\!\) is either \(v_j\!\) or \(\texttt{(} v_j \texttt{)},\) that is, either the assertion or the negation of the boolean variable \({v_j},\!\) as \(j\!\) runs from 1 to 57. Even more briefly, the same information can be communicated simply by giving the conjunction of the asserted variables, with the understanding that each of the others is negated.

A satisfying interpretation of the proposition \(p\!\) supplies us with all the information of a complete execution history for the corresponding program, and so all we have to do in order to get the output of the program \(p\!\) is to read off the proper part of the data from the expression of this interpretation.

Output

One component of the \(\begin{smallmatrix}\mathrm{Theme~One}\end{smallmatrix}\) program that I wrote some years ago finds all the satisfying interpretations of propositions expressed in cactus syntax. It's not a polynomial time algorithm, as you may guess, but it was just barely efficient enough to do this example in the 500 K of spare memory that I had on an old 286 PC in about 1989, so I will give you the actual outputs from those trials.

Output Conditions for Tape Input "0"

Let \(p_0\!\) be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "0" with the proposition that describes the truncated turing machine \(\mathrm{Stunt}(2).\) As it turns out, \(p_0\!\) has a single satisfying interpretation. This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display: 


o-------------------------------------------------o
|                                                 |
| p0_q0                                           |
|  p0_r1                                          |
|   p0_r0_s#                                      |
|    p0_r1_s0                                     |
|     p0_r2_s#                                    |
|      p1_q0                                      |
|       p1_r2                                     |
|        p1_r2_s#                                 |
|         p1_r0_s#                                |
|          p1_r1_s0                               |
|           p2_q#                                 |
|            p2_r1                                |
|             p2_r0_s#                            |
|              p2_r1_s0                           |
|               p2_r2_s#                          |
|                                                 |
o-------------------------------------------------o


The Output Conditions for Tape Input "0" can be read as follows:

At the time \(p_0,\!\) machine \(\mathrm{M}\) is in the state \(q_0,\!\) and

At the time \(p_0,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\) and

At the time \(p_0,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_0,\!\) cell \(r_1\!\) contains the symbol \(\texttt{0},\) and

At the time \(p_0,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_1,\!\) machine \(\mathrm{M}\) is in the state \(q_0,\!\) and

At the time \(p_1,\!\) scanner \(\mathrm{H}\) is reading cell \(r_2,\!\) and

At the time \(p_1,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_1,\!\) cell \(r_1\!\) contains the symbol \(\texttt{0},\) and

At the time \(p_1,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_2,\!\) machine \(\mathrm{M}\) is in the state \(q_\#,\!\) and

At the time \(p_2,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\) and

At the time \(p_2,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_2,\!\) cell \(r_1\!\) contains the symbol \(\texttt{0},\) and

At the time \(p_2,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#}.\)

The output of \(\mathrm{Stunt}(2)\) being the symbol that rests under the tape head \(\mathrm{H}\) if and when the machine \(\mathrm{M}\) reaches one of its resting states, we get the result that \(\mathrm{Parity}(0) = 0.\)

Output Conditions for Tape Input "1"

Let \(p_1\!\) be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "1" with the proposition that describes the truncated turing machine \(\mathrm{Stunt}(2).\) As it turns out, \(p_1\!\) has a single satisfying interpretation. This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display: 


o-------------------------------------------------o
|                                                 |
| p0_q0                                           |
|  p0_r1                                          |
|   p0_r0_s#                                      |
|    p0_r1_s1                                     |
|     p0_r2_s#                                    |
|      p1_q1                                      |
|       p1_r2                                     |
|        p1_r2_s#                                 |
|         p1_r0_s#                                |
|          p1_r1_s1                               |
|           p2_q*                                 |
|            p2_r1                                |
|             p2_r0_s#                            |
|              p2_r1_s1                           |
|               p2_r2_s#                          |
|                                                 |
o-------------------------------------------------o


The Output Conditions for Tape Input "1" can be read as follows:

At the time \(p_0,\!\) machine \(\mathrm{M}\) is in the state \(q_0,\!\) and

At the time \(p_0,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\) and

At the time \(p_0,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_0,\!\) cell \(r_1\!\) contains the symbol \(\texttt{1},\) and

At the time \(p_0,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_1,\!\) machine \(\mathrm{M}\) is in the state \(q_1,\!\) and

At the time \(p_1,\!\) scanner \(\mathrm{H}\) is reading cell \(r_2,\!\) and

At the time \(p_1,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_1,\!\) cell \(r_1\!\) contains the symbol \(\texttt{1},\) and

At the time \(p_1,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_2,\!\) machine \(\mathrm{M}\) is in the state \(q_*,\!\) and

At the time \(p_2,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\) and

At the time \(p_2,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_2,\!\) cell \(r_1\!\) contains the symbol \(\texttt{1},\) and

At the time \(p_2,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#}.\)

The output of \(\mathrm{Stunt}(2)\) being the symbol that rests under the tape head \(\mathrm{H}\) when and if the machine \(\mathrm{M}\) reaches one of its resting states, we get the result that \(\mathrm{Parity}(1) = 1.\)

Document History

Ontology List : Feb–Mar 2004

  1. http://suo.ieee.org/ontology/msg05457.html
  2. http://suo.ieee.org/ontology/msg05458.html
  3. http://suo.ieee.org/ontology/msg05459.html
  4. http://suo.ieee.org/ontology/msg05460.html
  5. http://suo.ieee.org/ontology/msg05461.html
  6. http://suo.ieee.org/ontology/msg05462.html
  7. http://suo.ieee.org/ontology/msg05463.html
  8. http://suo.ieee.org/ontology/msg05464.html
  9. http://suo.ieee.org/ontology/msg05465.html
  10. http://suo.ieee.org/ontology/msg05466.html
  11. http://suo.ieee.org/ontology/msg05467.html
  12. http://suo.ieee.org/ontology/msg05469.html
  13. http://suo.ieee.org/ontology/msg05470.html
  14. http://suo.ieee.org/ontology/msg05471.html
  15. http://suo.ieee.org/ontology/msg05472.html
  16. http://suo.ieee.org/ontology/msg05473.html
  17. http://suo.ieee.org/ontology/msg05474.html
  18. http://suo.ieee.org/ontology/msg05475.html
  19. http://suo.ieee.org/ontology/msg05476.html
  20. http://suo.ieee.org/ontology/msg05479.html

NKS Forum : Feb–Jun 2004

  1. http://forum.wolframscience.com/showthread.php?postid=664#post664
  2. http://forum.wolframscience.com/showthread.php?postid=666#post666
  3. http://forum.wolframscience.com/showthread.php?postid=677#post677
  4. http://forum.wolframscience.com/showthread.php?postid=684#post684
  5. http://forum.wolframscience.com/showthread.php?postid=689#post689
  6. http://forum.wolframscience.com/showthread.php?postid=697#post697
  7. http://forum.wolframscience.com/showthread.php?postid=708#post708
  8. http://forum.wolframscience.com/showthread.php?postid=721#post721
  9. http://forum.wolframscience.com/showthread.php?postid=722#post722
  10. http://forum.wolframscience.com/showthread.php?postid=725#post725
  11. http://forum.wolframscience.com/showthread.php?postid=733#post733
  12. http://forum.wolframscience.com/showthread.php?postid=756#post756
  13. http://forum.wolframscience.com/showthread.php?postid=759#post759
  14. http://forum.wolframscience.com/showthread.php?postid=764#post764
  15. http://forum.wolframscience.com/showthread.php?postid=766#post766
  16. http://forum.wolframscience.com/showthread.php?postid=767#post767
  17. http://forum.wolframscience.com/showthread.php?postid=773#post773
  18. http://forum.wolframscience.com/showthread.php?postid=775#post775
  19. http://forum.wolframscience.com/showthread.php?postid=777#post777
  20. http://forum.wolframscience.com/showthread.php?postid=791#post791
  21. http://forum.wolframscience.com/showthread.php?postid=1458#post1458
  22. http://forum.wolframscience.com/showthread.php?postid=1461#post1461
  23. http://forum.wolframscience.com/showthread.php?postid=1463#post1463
  24. http://forum.wolframscience.com/showthread.php?postid=1464#post1464
  25. http://forum.wolframscience.com/showthread.php?postid=1467#post1467
  26. http://forum.wolframscience.com/showthread.php?postid=1469#post1469
  27. http://forum.wolframscience.com/showthread.php?postid=1470#post1470
  28. http://forum.wolframscience.com/showthread.php?postid=1471#post1471
  29. http://forum.wolframscience.com/showthread.php?postid=1473#post1473
  30. http://forum.wolframscience.com/showthread.php?postid=1475#post1475
  31. http://forum.wolframscience.com/showthread.php?postid=1479#post1479
  32. http://forum.wolframscience.com/showthread.php?postid=1489#post1489
  33. http://forum.wolframscience.com/showthread.php?postid=1490#post1490

Inquiry List : Feb–Jun 2004

  1. http://stderr.org/pipermail/inquiry/2004-February/001228.html
  2. http://stderr.org/pipermail/inquiry/2004-February/001230.html
  3. http://stderr.org/pipermail/inquiry/2004-February/001231.html
  4. http://stderr.org/pipermail/inquiry/2004-February/001232.html
  5. http://stderr.org/pipermail/inquiry/2004-February/001233.html
  6. http://stderr.org/pipermail/inquiry/2004-February/001234.html
  7. http://stderr.org/pipermail/inquiry/2004-March/001235.html
  8. http://stderr.org/pipermail/inquiry/2004-March/001236.html
  9. http://stderr.org/pipermail/inquiry/2004-March/001237.html
  10. http://stderr.org/pipermail/inquiry/2004-March/001238.html
  11. http://stderr.org/pipermail/inquiry/2004-March/001240.html
  12. http://stderr.org/pipermail/inquiry/2004-March/001242.html
  13. http://stderr.org/pipermail/inquiry/2004-March/001243.html
  14. http://stderr.org/pipermail/inquiry/2004-March/001244.html
  15. http://stderr.org/pipermail/inquiry/2004-March/001245.html
  16. http://stderr.org/pipermail/inquiry/2004-March/001246.html
  17. http://stderr.org/pipermail/inquiry/2004-March/001247.html
  18. http://stderr.org/pipermail/inquiry/2004-March/001248.html
  19. http://stderr.org/pipermail/inquiry/2004-March/001249.html
  20. http://stderr.org/pipermail/inquiry/2004-March/001255.html
  21. http://stderr.org/pipermail/inquiry/2004-June/001630.html
  22. http://stderr.org/pipermail/inquiry/2004-June/001631.html
  23. http://stderr.org/pipermail/inquiry/2004-June/001632.html
  24. http://stderr.org/pipermail/inquiry/2004-June/001633.html
  25. http://stderr.org/pipermail/inquiry/2004-June/001634.html
  26. http://stderr.org/pipermail/inquiry/2004-June/001635.html
  27. http://stderr.org/pipermail/inquiry/2004-June/001636.html
  28. http://stderr.org/pipermail/inquiry/2004-June/001637.html
  29. http://stderr.org/pipermail/inquiry/2004-June/001638.html
  30. http://stderr.org/pipermail/inquiry/2004-June/001639.html
  31. http://stderr.org/pipermail/inquiry/2004-June/001640.html
  32. http://stderr.org/pipermail/inquiry/2004-June/001641.html
  33. http://stderr.org/pipermail/inquiry/2004-June/001642.html
Retrieved from "https://mywikibiz.com/index.php?title=Directory:Jon_Awbrey/Papers/Differential_Analytic_Turing_Automata&oldid=228459"