Difference between revisions of "Golden Diagram"
Drlesmgolden (talk | contribs) (Created page with "'''The Golden Diagram''' is a contour diagram which summarizes the levels of probability of attaining a given advantage in the card game of blackjack depending on the number o...") |
Drlesmgolden (talk | contribs) |
||
| Line 9: | Line 9: | ||
==The Golden Diagram== | ==The Golden Diagram== | ||
None of the above phenomena were quantified. Based on Monte Carlo calculations and the application of a modified central limit theorem, Les Golden quantified these effects and indicated how players can regain some of their lost advantage by variations in strategy and a suggested betting sequence. | None of the above phenomena were quantified. Based on Monte Carlo calculations and the application of a modified central limit theorem, Les Golden quantified these effects and indicated how players can regain some of their lost advantage by variations in strategy and a suggested betting sequence. | ||
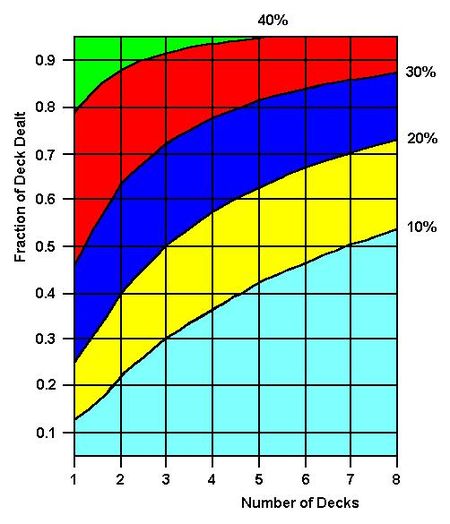
| − | The step-wise betting strategy based on these findings was shown to increase the player's expected winnings by a factor of up to 2.6. [[File: | + | The step-wise betting strategy based on these findings was shown to increase the player's expected winnings by a factor of up to 2.6. [[File: Goldendiagrama.JPG|450px|thumb|right|<small> The Golden Diagram for a value of high-low index of +6 in the complete point count system of Edward O. Thorp. At given depths into deck packs noted, the curved lines provide the probability that the deck will achieve the high-low index value of +6.</small>]] |
==Advantages to Card Counters== | ==Advantages to Card Counters== | ||
Latest revision as of 17:02, 20 June 2017
The Golden Diagram is a contour diagram which summarizes the levels of probability of attaining a given advantage in the card game of blackjack depending on the number of decks in use and the depth to which the deck has been played. It was developed by blackjack professional, writer, and mathematician Dr. Leslie M. Golden of Oak Park, Illinois in 2011 and published in the peer-reviewed scholarly journal The Mathematical Scientist as well as in a series of articles in Bluff Europe magazine.[1][2]
Card Counting
In the early 1960's, Edward Thorp[3] in collaboration with Julian Braun and Harvey Dubner, utilized electronic computing to devise a strategy for the game of 21 based on its being a game of statistics without replacement. As a result of the publication of Thorp's book Beat the Dealer[4], readily accessible to the lay public, what had been a relatively unpopular casino game has in the decades since become the overwhelmingly most popular casino game. Casinos reacted to the advantage that a strategic player gains over the house by changing some of the rules of the game and by adopting counter strategies. These included not dealing to the end of the deck and employing multiple decks rather than the single hand-held deck. Two-deck games and games employing four and six decks dealt from a so-called shoe became commonplace. Players soon realized intuitively that both these changes in the game reduced their probabilities of winning. In games with a multiple deck, compared to single-deck or double-deck games, players experience frequency, magnitude, and "depth" (the fraction of the deck which has been dealt in playing previous hands) effects: 1) The deck becomes favorable less frequently at all depths, 2) when the deck does becomes favorable, the magnitude of the advantage is not as great, 3) all decks are favorable infrequently until a significant portion of the deck has been dealt and this occurs at greater depths into the deck in games using multiple decks. The latter follows from the phenomenon that the "spread" in the distribution of player expectations increases as cards are dealt out of the deck; this is referred to as the "fundamental theorem of card counting" by Thorp and Walden. Proofs under the assumption of a fixed player strategy, one in which neither the strategy nor bet size are varied as the cards are played, were provided by both Thorp and Walden and Ethier and Levin[5][6].
The Golden Diagram
None of the above phenomena were quantified. Based on Monte Carlo calculations and the application of a modified central limit theorem, Les Golden quantified these effects and indicated how players can regain some of their lost advantage by variations in strategy and a suggested betting sequence.
The step-wise betting strategy based on these findings was shown to increase the player's expected winnings by a factor of up to 2.6.
Advantages to Card Counters
Using the stepwise betting system has several advantages for players. First, it does not change from deck to deck. Changing a bet when the deck becomes favorable is a tip-off to the casino that the player is a card-counter. The system developed by Golden requires a step-wise betting sequence which is independent of the quality of the deck.
References
- ^ Golden, Leslie M. (2011). “An Analysis of the Disadvantage to Players of Multiple Decks in the Game of 21.” The Mathematical Scientist, 32, 2, p. 57-69
- ^ Golden, Les (2011). “Stepping Out With My Baby: The Stepwise Betting Strategy,” Bluff Europe, April, p. 92-93
- ^ Thorp, E. O. [1961] A favorable strategy for twenty-one, Proceedings of the National Academy of Sciences
- ^ Thorp, E. O. [1962, 1966] Beat the Dealer: A Winning Strategy for the Game of Twenty-One, Random House, New York
- ^ Thorp, E. O. and Walden, W. E. [1973]. The fundamental theorem of card counting with applications to trente-et-quarante and baccarat, Internat. J. Game Theory 2, 109-119
- ^ Ethier, S.N. and D. A. Levin, D.A. [2005] On the fundamental theorem of card counting, with application to the game of trente et quarante, Adv. in Appl. Probab. Vol. 37, No. 1, 90-107
Categories
- Academia
- American academics
- American essayists
- Betting systems
- Research
- Gambling
- Gambling games
- Gambling terminology
- American non-fiction writers
- American writers
- Politics
- Probability theory
- Jewish writers
- Jewish academics
- Jewish gambling writers
- Jewish astronomers
- Notable residents of Oak Park Illinois
- Notable residents of Illinois
- Gambling writers
- American computer programmers
- American people of Jewish descent
- American people of Polish-Jewish descent
- American scientists
- Authors
- Blackjack
- Celebrities
- Celebrity Interviews
- Jewish American writers
- Jewish scientists