Difference between revisions of "Minimal negation operator"
Jon Awbrey (talk | contribs) (→Truth tables: HTML → LaTeX) |
Jon Awbrey (talk | contribs) (→Truth tables: PNG) |
||
| Line 24: | Line 24: | ||
Table 1 is a [[truth table]] for the sixteen boolean functions of type <math>f : \mathbb{B}^3 \to \mathbb{B}</math> whose fibers of 1 are either the boundaries of points in <math>\mathbb{B}^3</math> or the complements of those boundaries. | Table 1 is a [[truth table]] for the sixteen boolean functions of type <math>f : \mathbb{B}^3 \to \mathbb{B}</math> whose fibers of 1 are either the boundaries of points in <math>\mathbb{B}^3</math> or the complements of those boundaries. | ||
| + | <br> | ||
{| align="center" border="1" cellpadding="4" cellspacing="0" style="background:whitesmoke; font-weight:bold; text-align:center; width:80%" | {| align="center" border="1" cellpadding="4" cellspacing="0" style="background:whitesmoke; font-weight:bold; text-align:center; width:80%" | ||
|+ Table 1. Logical Boundaries and Their Complements | |+ Table 1. Logical Boundaries and Their Complements | ||
| Line 53: | Line 54: | ||
{| align="center" border="1" cellpadding="4" cellspacing="0" style="background:ghostwhite; font-weight:bold; text-align:center; width:80%" | {| align="center" border="1" cellpadding="4" cellspacing="0" style="background:ghostwhite; font-weight:bold; text-align:center; width:80%" | ||
|- | |- | ||
| − | | width="20%" | <math>f_{104}</math> | + | | width="20%" | <math>f_{104}\!</math> |
| − | | width="20%" | <math>f_{01101000}</math> | + | | width="20%" | <math>f_{01101000}\!</math> |
| width="20%" | 0 1 1 0 1 0 0 0 | | width="20%" | 0 1 1 0 1 0 0 0 | ||
| − | | width="20%" | <math>( p , q , r )</math> | + | | width="20%" | <math>( p , q , r )\!</math> |
|- | |- | ||
| − | | <math>f_{148}</math> | + | | <math>f_{148}\!</math> |
| − | | <math>f_{10010100}</math> | + | | <math>f_{10010100}\!</math> |
| 1 0 0 1 0 1 0 0 | | 1 0 0 1 0 1 0 0 | ||
| − | | <math>( p , q , (r))</math> | + | | <math>( p , q , (r))\!</math> |
|- | |- | ||
| − | | <math>f_{146}</math> | + | | <math>f_{146}\!</math> |
| − | | <math>f_{10010010}</math> | + | | <math>f_{10010010}\!</math> |
| 1 0 0 1 0 0 1 0 | | 1 0 0 1 0 0 1 0 | ||
| − | | <math>( p , (q), r )</math> | + | | <math>( p , (q), r )\!</math> |
|- | |- | ||
| − | | <math>f_{97}</math> | + | | <math>f_{97}\!</math> |
| − | | <math>f_{01100001}</math> | + | | <math>f_{01100001}\!</math> |
| 0 1 1 0 0 0 0 1 | | 0 1 1 0 0 0 0 1 | ||
| − | | <math>( p , (q), (r))</math> | + | | <math>( p , (q), (r))\!</math> |
|- | |- | ||
| − | | <math>f_{134}</math> | + | | <math>f_{134}\!</math> |
| − | | <math>f_{10000110}</math> | + | | <math>f_{10000110}\!</math> |
| 1 0 0 0 0 1 1 0 | | 1 0 0 0 0 1 1 0 | ||
| − | | <math>((p), q , r )</math> | + | | <math>((p), q , r )\!</math> |
|- | |- | ||
| − | | <math>f_{73}</math> | + | | <math>f_{73}\!</math> |
| − | | <math>f_{01001001}</math> | + | | <math>f_{01001001}\!</math> |
| 0 1 0 0 1 0 0 1 | | 0 1 0 0 1 0 0 1 | ||
| − | | <math>((p), q , (r))</math> | + | | <math>((p), q , (r))\!</math> |
|- | |- | ||
| − | | <math>f_{41}</math> | + | | <math>f_{41}\!</math> |
| − | | <math>f_{00101001}</math> | + | | <math>f_{00101001}\!</math> |
| 0 0 1 0 1 0 0 1 | | 0 0 1 0 1 0 0 1 | ||
| − | | <math>((p), (q), r )</math> | + | | <math>((p), (q), r )\!</math> |
|- | |- | ||
| − | | <math>f_{22}</math> | + | | <math>f_{22}\!</math> |
| − | | <math>f_{00010110}</math> | + | | <math>f_{00010110}\!</math> |
| 0 0 0 1 0 1 1 0 | | 0 0 0 1 0 1 1 0 | ||
| − | | <math>((p), (q), (r))</math> | + | | <math>((p), (q), (r))\!</math> |
|} | |} | ||
{| align="center" border="1" cellpadding="4" cellspacing="0" style="background:ghostwhite; font-weight:bold; text-align:center; width:80%" | {| align="center" border="1" cellpadding="4" cellspacing="0" style="background:ghostwhite; font-weight:bold; text-align:center; width:80%" | ||
|- | |- | ||
| − | | width="20%" | <math>f_{233}</math> | + | | width="20%" | <math>f_{233}\!</math> |
| − | | width="20%" | <math>f_{11101001}</math> | + | | width="20%" | <math>f_{11101001}\!</math> |
| width="20%" | 1 1 1 0 1 0 0 1 | | width="20%" | 1 1 1 0 1 0 0 1 | ||
| − | | width="20%" | <math>(((p), (q), (r)))</math> | + | | width="20%" | <math>(((p), (q), (r)))\!</math> |
|- | |- | ||
| − | | <math>f_{214}</math> | + | | <math>f_{214}\!</math> |
| − | | <math>f_{11010110}</math> | + | | <math>f_{11010110}\!</math> |
| 1 1 0 1 0 1 1 0 | | 1 1 0 1 0 1 1 0 | ||
| − | | <math>(((p), (q), r ))</math> | + | | <math>(((p), (q), r ))\!</math> |
|- | |- | ||
| − | | <math>f_{182}</math> | + | | <math>f_{182}\!</math> |
| − | | <math>f_{10110110}</math> | + | | <math>f_{10110110}\!</math> |
| 1 0 1 1 0 1 1 0 | | 1 0 1 1 0 1 1 0 | ||
| − | | <math>(((p), q , (r)))</math> | + | | <math>(((p), q , (r)))\!</math> |
|- | |- | ||
| − | | <math>f_{121}</math> | + | | <math>f_{121}\!</math> |
| − | | <math>f_{01111001}</math> | + | | <math>f_{01111001}\!</math> |
| 0 1 1 1 1 0 0 1 | | 0 1 1 1 1 0 0 1 | ||
| − | | <math>(((p), q , r ))</math> | + | | <math>(((p), q , r ))\!</math> |
|- | |- | ||
| − | | <math>f_{158}</math> | + | | <math>f_{158}\!</math> |
| − | | <math>f_{10011110}</math> | + | | <math>f_{10011110}\!</math> |
| 1 0 0 1 1 1 1 0 | | 1 0 0 1 1 1 1 0 | ||
| − | | <math>(( p , (q), (r)))</math> | + | | <math>(( p , (q), (r)))\!</math> |
|- | |- | ||
| − | | <math>f_{109}</math> | + | | <math>f_{109}\!</math> |
| − | | <math>f_{01101101}</math> | + | | <math>f_{01101101}\!</math> |
| 0 1 1 0 1 1 0 1 | | 0 1 1 0 1 1 0 1 | ||
| − | | <math>(( p , (q), r ))</math> | + | | <math>(( p , (q), r ))\!</math> |
|- | |- | ||
| − | | <math>f_{107}</math> | + | | <math>f_{107}\!</math> |
| − | | <math>f_{01101011}</math> | + | | <math>f_{01101011}\!</math> |
| 0 1 1 0 1 0 1 1 | | 0 1 1 0 1 0 1 1 | ||
| − | | <math>(( p , q , (r)))</math> | + | | <math>(( p , q , (r)))\!</math> |
|- | |- | ||
| − | | <math>f_{151}</math> | + | | <math>f_{151}\!</math> |
| − | | <math>f_{10010111}</math> | + | | <math>f_{10010111}\!</math> |
| 1 0 0 1 0 1 1 1 | | 1 0 0 1 0 1 1 1 | ||
| − | | <math>(( p , q , r ))</math> | + | | <math>(( p , q , r ))\!</math> |
|} | |} | ||
<br> | <br> | ||
Revision as of 17:18, 20 May 2009
In logic and mathematics, the minimal negation operator \(\nu\!\) is a multigrade operator \((\nu_k)_{k \in \mathbb{N}}\) where each \(\nu_k\!\) is a \(k\!\)-ary boolean function defined in such a way that \(\nu_k (x_1, \ldots , x_k) = 1\) if and only if exactly one of the arguments \(x_j\!\) is \(0.\!\)
In contexts where the initial letter \(\nu\!\) is understood, the minimal negation operators can be indicated by argument lists in parentheses. The first four members of this family of operators are shown below, with paraphrases in a couple of other notations, where tildes and primes, respectively, indicate logical negation.
|
\(\begin{matrix} (~) & = & 0 & = & \operatorname{false} \'"`UNIQ-MathJax1-QINU`"' * The point \((0, 0, \ldots , 0, 0)\) with all 0's as coordinates is the point where the conjunction of all negated variables evaluates to 1, namely, the point where:
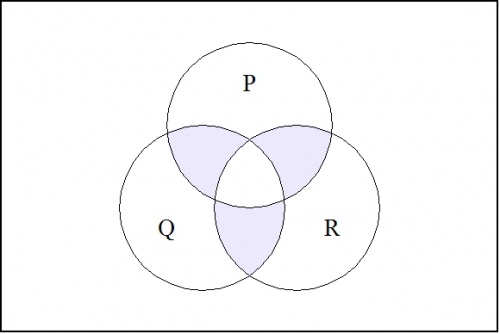
To pass from these limiting examples to the general case, observe that a singular proposition s : Bk → B can be given canonical expression as a conjunction of literals, \(s = e_1 e_2 \ldots e_{k-1} e_k\). Then the proposition \(\nu (e_1, e_2, \ldots, e_{k-1}, e_k)\) is 1 on the points adjacent to the point where s is 1, and 0 everywhere else on the cube. For example, consider the case where k = 3. Then the minimal negation operation \(\nu (p, q, r)\!\), when there is no risk of confusion written more simply as \((p, q, r)\!\), has the following venn diagram:
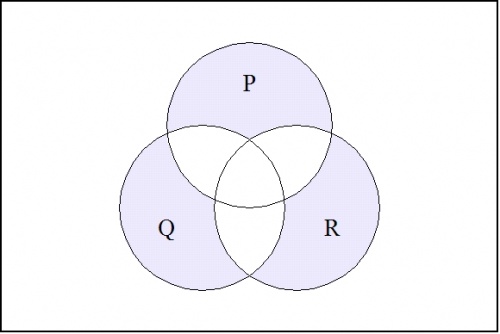
For a contrasting example, the boolean function expressed by the form \(((p),(q),(r))\!\) has the following venn diagram:
Glossary of basic terms
See alsoTemplate:Col-break
External linksAficionados
<sharethis /> |