Minimal negation operator

In logic and mathematics, the minimal negation operator \(\nu\!\) is a multigrade operator \((\nu_k)_{k \in \mathbb{N}}\) where each \(\nu_k\!\) is a \(k\!\)-ary boolean function defined in such a way that \(\nu_k (x_1, \ldots , x_k) = 1\) if and only if exactly one of the arguments \(x_j\!\) is \(0.\!\)

In contexts where the initial letter \(\nu\!\) is understood, the minimal negation operators can be indicated by argument lists in parentheses. The first four members of this family of operators are shown below, with paraphrases in a couple of other notations, where tildes and primes, respectively, indicate logical negation.

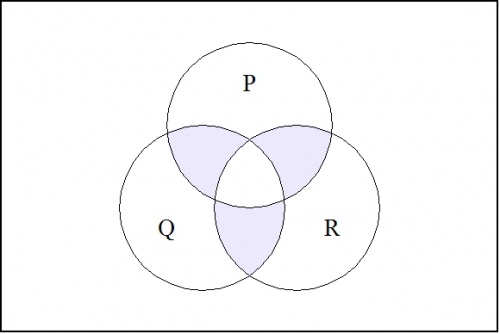
\(\begin{matrix} \texttt{(~)} & = & 0 & = & \operatorname{false} \'"`UNIQ-MathJax1-QINU`"' * The point \((0, 0, \ldots , 0, 0)\) with all 0's as coordinates is the point where the conjunction of all negated variables evaluates to \(1,\!\) namely, the point where: \[(x_1)(x_2)\ldots(x_{n-1})(x_n) = 1.\] To pass from these limiting examples to the general case, observe that a singular proposition \(s : \mathbb{B}^k \to \mathbb{B}\) can be given canonical expression as a conjunction of literals, \(s = e_1 e_2 \ldots e_{k-1} e_k\). Then the proposition \(\nu (e_1, e_2, \ldots, e_{k-1}, e_k)\) is \(1\!\) on the points adjacent to the point where \(s\!\) is \(1,\!\) and 0 everywhere else on the cube. 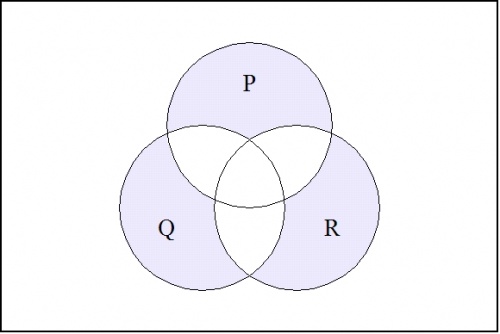For example, consider the case where \(k = 3.\!\) Then the minimal negation operation \(\nu (p, q, r)\!\), when there is no risk of confusion written more simply as \((p, q, r)\!\), has the following venn diagram: \(\text{Figure 1.}\quad (p, q, r)\!\) For a contrasting example, the boolean function expressed by the form \(((p),(q),(r))\!\) has the following venn diagram: \(\text{Figure 2.}\quad ((p),(q),(r))\!\) Glossary of basic terms Boolean domain A boolean domain \(\mathbb{B}\) is a generic 2-element set, for example, \(\mathbb{B} = \{ 0, 1 \},\) whose elements are interpreted as logical values, usually but not invariably with \(0 = \operatorname{false}\) and \(1 = \operatorname{true}.\) Boolean variable A boolean variable \(x\!\) is a variable that takes its value from a boolean domain, as \(x \in \mathbb{B}.\) Proposition In situations where boolean values are interpreted as logical values, a boolean-valued function \(f : X \to \mathbb{B}\) or a boolean function \(g : \mathbb{B}^k \to \mathbb{B}\) is frequently called a proposition. Basis element, Coordinate projection Given a sequence of \(k\!\) boolean variables, \(x_1, \ldots, x_k,\) each variable \(x_j\!\) may be treated either as a basis element of the space \(\mathbb{B}^k\) or as a coordinate projection \(x_j : \mathbb{B}^k \to \mathbb{B}.\) Basic proposition This means that the set of objects \(\{ x_j : 1 \le j \le k \}\) is a set of boolean functions \(\{ x_j : \mathbb{B}^k \to \mathbb{B} \}\) subject to logical interpretation as a set of basic propositions that collectively generate the complete set of \(2^{2^k}\) propositions over \(\mathbb{B}^k.\) Literal A literal is one of the \(2k\!\) propositions \(x_1, \ldots, x_k, (x_1), \ldots, (x_k),\) in other words, either a posited basic proposition \(x_j\!\) or a negated basic proposition \((x_j),\!\) for some \(j = 1 ~\text{to}~ k.\) Fiber In mathematics generally, the fiber of a point \(y \in Y\) under a function \(f : X \to Y\) is defined as the inverse image \(f^{-1}(y) \subseteq X.\) In the case of a boolean function \(f : \mathbb{B}^k \to \mathbb{B},\) there are just two fibers: The fiber of \(0\!\) under \(f,\!\) defined as \(f^{-1}(0),\!\) is the set of points where the value of \(f\!\) is \(0.\!\) The fiber of \(1\!\) under \(f,\!\) defined as \(f^{-1}(1),\!\) is the set of points where the value of \(f\!\) is \(1.\!\) Fiber of truth When \(1\!\) is interpreted as the logical value \(\operatorname{true},\) then \(f^{-1}(1)\!\) is called the fiber of truth in the proposition \(f.\!\) Frequent mention of this fiber makes it useful to have a shorter way of referring to it. This leads to the definition of the notation \([|f|] = f^{-1}(1)\!\) for the fiber of truth in the proposition \(f.\!\) Singular boolean function A singular boolean function \(s : \mathbb{B}^k \to \mathbb{B}\) is a boolean function whose fiber of \(1\!\) is a single point of \(\mathbb{B}^k.\) Singular proposition In the interpretation where \(1\!\) equals \(\operatorname{true},\) a singular boolean function is called a singular proposition. Singular boolean functions and singular propositions serve as functional or logical representatives of the points in \(\mathbb{B}^k.\) Singular conjunction A singular conjunction in \(\mathbb{B}^k \to \mathbb{B}\) is a conjunction of \(k\!\) literals that includes just one conjunct of the pair \(\{ x_j, ~\nu(x_j) \}\) for each \(j = 1 ~\text{to}~ k.\) A singular proposition \(s : \mathbb{B}^k \to \mathbb{B}\) can be expressed as a singular conjunction: \(s ~=~ e_1 e_2 \ldots e_{k-1} e_k\), \(\begin{array}{llll} \text{where} & e_j & = & x_j \\[6pt] \text{or} & e_j & = & \nu (x_j), \\[6pt] \text{for} & j & = & 1 ~\text{to}~ k. \end{array}\) See also Template:Col-break Ampheck Anamnesis BACD Boole, George Boolean algebra Boolean function Boolean logic Boolean-valued function Template:Col-break Continuous predicate Differentiable manifold Differential topology Dynamical system Exclusive disjunction Leibniz, G.W. Logical connective Logical graph Template:Col-break Meno Multigrade operator Parametric operator Peirce, C.S. Sole sufficient operator Truth table Universal algebra Zeroth order logic Template:Col-end External links Minimal Negation Operator @ PlanetMath Minimal Negation Operator @ PlanetPhysics Wolfram Atlas of Simple Programs Elementary Cellular Automata Rules (ECARs) ECAR Index ECAR Icons ECAR Examples ECAR Formulas Aficionados See Talk:Minimal negation operator for discussions/comments regarding this article. See Minimal negation operator/Aficionados for those who have listed Minimal negation operator as an interest. See Talk:Minimal negation operator/Aficionados for discussions regarding this interest. <sharethis />