Difference between revisions of "Directory:Jon Awbrey/Papers/Differential Analytic Turing Automata"

MyWikiBiz, Author Your Legacy — Sunday November 17, 2024
Jump to navigationJump to search
(update)
(update)
Line 4: Line 4:
 
The task ahead is to chart a course from general ideas about ''transformational equivalence classes of graphs'' to a notion of ''differential analytic turing automata'' (DATA).  It may be a while before we get within sight of that goal, but it will provide a better measure of motivation to name the thread after the envisioned end rather than the more homely starting place.
 
The task ahead is to chart a course from general ideas about ''transformational equivalence classes of graphs'' to a notion of ''differential analytic turing automata'' (DATA).  It may be a while before we get within sight of that goal, but it will provide a better measure of motivation to name the thread after the envisioned end rather than the more homely starting place.
  
−
The basic idea is as follows.  One has a set <math>\mathcal{G}</math> of graphs and a set <math>\mathcal{T}</math> of transformation rules, and each rule <math>\operatorname{t} \in \mathcal{T}</math> has the effect of transforming graphs into graphs, <math>\operatorname{t} : \mathcal{G} \to \mathcal{G}.</math>  In the cases that we shall be studying, this set of transformation rules partitions the set of graphs into ''transformational equivalence classes'' (TECs).
+
The basic idea is as follows.  One has a set <math>\mathcal{G}</math> of graphs and a set <math>\mathcal{T}</math> of transformation rules, and each rule <math>\mathrm{t} \in \mathcal{T}</math> has the effect of transforming graphs into graphs, <math>\mathrm{t} : \mathcal{G} \to \mathcal{G}.</math>  In the cases that we shall be studying, this set of transformation rules partitions the set of graphs into ''transformational equivalence classes'' (TECs).
  
 
There are many interesting excursions to be had here, but I will focus mainly on logical applications, and and so the TECs I talk about will almost always have the character of ''logical equivalence classes'' (LECs).
 
There are many interesting excursions to be had here, but I will focus mainly on logical applications, and and so the TECs I talk about will almost always have the character of ''logical equivalence classes'' (LECs).
Line 581: Line 581:
 
|}
 
|}
  
−
Given any transformation of this type, <math>G : U^\bullet \to X^\bullet,\!</math> the (first order) differential analysis of <math>G\!</math> is based on the definition of a couple of further transformations, derived by way of operators on <math>G,\!</math> that ply between the (first order) extended universes, <math>\mathrm{E}U^\bullet = [u, v, du, dv]\!</math> and <math>\operatorname{E}X^\bullet = [x, y, dx, dy],\!</math> of <math>G\text{'s}\!</math> own source and target universes.
+
Given any transformation of this type, <math>G : U^\bullet \to X^\bullet,\!</math> the (first order) differential analysis of <math>G\!</math> is based on the definition of a couple of further transformations, derived by way of operators on <math>G,\!</math> that ply between the (first order) extended universes, <math>\mathrm{E}U^\bullet = [u, v, du, dv]\!</math> and <math>\mathrm{E}X^\bullet = [x, y, dx, dy],\!</math> of <math>G\text{'s}\!</math> own source and target universes.
  
 
First, the ''enlargement map'' (or the ''secant transformation'') <math>\mathrm{E}G = (\mathrm{E}G_1, \mathrm{E}G_2) : \mathrm{E}U^\bullet \to \mathrm{E}X^\bullet\!</math> is defined by the following pair of component equations:
 
First, the ''enlargement map'' (or the ''secant transformation'') <math>\mathrm{E}G = (\mathrm{E}G_1, \mathrm{E}G_2) : \mathrm{E}U^\bullet \to \mathrm{E}X^\bullet\!</math> is defined by the following pair of component equations:
Line 671: Line 671:
 
|
 
|
 
<math>\begin{array}{ll}
 
<math>\begin{array}{ll}
−
1.1. & f : \mathbb{B} \to \mathbb{B} ~\text{such that}~ f : \texttt{x} \mapsto \texttt{(x)}
+
1.1. & f : \mathbb{B} \to \mathbb{B} ~\text{such that}~ f : x \mapsto \texttt{(} x \texttt{)}
 
\\
 
\\
−
1.2. & \texttt{x}' ~=~ \texttt{(x)}
+
1.2. & x' ~=~ \texttt{(} x \texttt{)}
 
\\
 
\\
−
1.3. & \texttt{x} ~:=~ \texttt{(x)}
+
1.3. & x ~:=~ \texttt{(} x \texttt{)}
 
\\
 
\\
−
1.4. & \texttt{dx} ~=~ \texttt{1}
+
1.4. & \mathrm{d}x ~=~ 1
 
\end{array}</math>
 
\end{array}</math>
 
|}
 
|}
Line 686: Line 686:
 
|
 
|
 
<math>\begin{array}{ll}
 
<math>\begin{array}{ll}
−
2.1. & F : \mathbb{B}^2 \to \mathbb{B}^2 ~\text{such that}~ F : (\texttt{u}, \texttt{v}) \mapsto ( ~\texttt{((u)(v))}~ , ~\texttt{((u,~v))}~ )
+
2.1. & F : \mathbb{B}^2 \to \mathbb{B}^2 ~\text{such that}~ F : (u, v) \mapsto ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ )
 
\\
 
\\
−
2.2. & \texttt{u}' ~=~ \texttt{((u)(v))}~, \quad \texttt{v}' ~=~ \texttt{((u,~v))}
+
2.2. & u' ~=~ \texttt{((} u \texttt{)(} v \texttt{))} \quad ~,~ \quad v' ~=~ \texttt{((} u \texttt{,~} v \texttt{))}
 
\\
 
\\
−
2.3. & \texttt{u} ~:=~ \texttt{((u)(v))}~, \quad \texttt{v} ~:=~ \texttt{((u,~v))}
+
2.3. & u ~:=~ \texttt{((} u \texttt{)(} v \texttt{))} \quad ~,~ \quad v ~:=~ \texttt{((} u \texttt{,~} v \texttt{))}
 
\\
 
\\
−
2.4. & ???
+
2.4. & ?
 
\end{array}</math>
 
\end{array}</math>
 
|}
 
|}
  
−
Well, the last one is not such a fall off the log, but that is exactly the purpose for which we have been developing all of the foregoing machinations.
+
Well, the last one is not such a fall off a log, but that is exactly the purpose for which we have been developing all of the foregoing machinations.
  
 
Here is what I got when I just went ahead and calculated the finite differences willy-nilly:
 
Here is what I got when I just went ahead and calculated the finite differences willy-nilly:
Line 702: Line 702:
 
{| align="center" cellpadding="8" style="text-align:center"
 
{| align="center" cellpadding="8" style="text-align:center"
 
|-
 
|-
−
| <math>\text{Orbit 1. Intitial Point :}~ (u, v) = (1, 1)</math>
+
| <math>\text{Orbit 1. Intitial Point :}~ (u, v) = (1, 1)\!</math>
 
|-
 
|-
 
|
 
|
 
<math>\begin{array}{c|cc|cc|cc|cc|cc|c}
 
<math>\begin{array}{c|cc|cc|cc|cc|cc|c}
−
t & u & v & du & dv & d^2 u & d^2 v & d^3 u & d^3 v & d^4 u & d^4 v & \ldots \\
+
t & u & v & \mathrm{d}u & \mathrm{d}v & \mathrm{d}^2 u & \mathrm{d}^2 v & \mathrm{d}^3 u & \mathrm{d}^3 v & \mathrm{d}^4 u & \mathrm{d}^4 v & \ldots \\[8pt]
−
\\
+
0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ldots \\
−
0 & 1 & 1 & 0 & 0 &     0 &     0 &     0 &     0 &     0 &     0 & \ldots \\
+
1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ldots \\
−
1 & 1 & 1 & 0 & 0 &     0 &     0 &     0 &     0 &     0 &     0 & \ldots \\
+
2 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & \ldots
−
4 & '' & '' & '' & '' &   '' &   '' &   '' &   '' &   '' &   '' & \ldots \\
 
 
\end{array}</math>
 
\end{array}</math>
 
|-
 
|-
−
| <math>\text{Orbit 2. Intitial Point :}~ (u, v) = (0, 0)</math>
+
| <math>\text{Orbit 2. Intitial Point :}~ (u, v) = (0, 0)\!</math>
 
|-
 
|-
 
|
 
|
 
<math>\begin{array}{c|cc|cc|cc|cc|cc|c}
 
<math>\begin{array}{c|cc|cc|cc|cc|cc|c}
−
t & u & v & du & dv & d^2 u & d^2 v & d^3 u & d^3 v & d^4 u & d^4 v & \ldots \\
+
t & u & v & \mathrm{d}u & \mathrm{d}v & \mathrm{d}^2 u & \mathrm{d}^2 v & \mathrm{d}^3 u & \mathrm{d}^3 v & \mathrm{d}^4 u & \mathrm{d}^4 v & \ldots \\[8pt]
−
\\
+
0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & \ldots \\
−
0 & 0 & 0 & 0 & 1 &     1 &     0 &     0 &     1 &     1 &     0 & \ldots \\
+
1 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & \ldots \\
−
1 & 0 & 1 & 1 & 1 &     1 &     1 &     1 &     1 &     1 &     1 & \ldots \\
+
2 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ldots \\
−
2 & 1 & 0 & 0 & 0 &     0 &     0 &     0 &     0 &     0 &     0 & \ldots \\
+
3 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ldots \\
−
3 & 1 & 0 & 0 & 0 &     0 &     0 &     0 &     0 &     0 &     0 & \ldots \\
+
4 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & \ldots
−
4 & '' & '' & '' & '' &   '' &   '' &   '' &   '' &   '' &   '' & \ldots \\
 
 
\end{array}</math>
 
\end{array}</math>
 
|}
 
|}
Line 731: Line 729:
 
What we are looking for is &mdash; one rule to rule them all, a rule that applies to every state and works every time.
 
What we are looking for is &mdash; one rule to rule them all, a rule that applies to every state and works every time.
  
−
What we see at first sight in the tables above are patterns of differential features that attach to the states in each orbit of the dynamics.  Looked at locally to these orbits, the isolated fixed point at <math>(1, 1)\!</math> is no problem, as the rule <math>\texttt{du~=~dv~=~0}</math> describes it pithily enough.  When it comes to the other orbit, the first thing that comes to mind is to write out the law <math>\texttt{du~=~v}, ~\texttt{dv~=~(u)}.</math>
+
What we see at first sight in the tables above are patterns of differential features that attach to the states in each orbit of the dynamics.  Looked at locally to these orbits, the isolated fixed point at <math>(1, 1)\!</math> is no problem, as the rule <math>\mathrm{d}u = \mathrm{d}v = 0\!</math> describes it pithily enough.  When it comes to the other orbit, the first thing that comes to mind is to write out the law <math>\mathrm{d}u = v ~,~ \mathrm{d}v = \texttt{(} u \texttt{)}.\!</math>
  
 
==Symbolic Method==
 
==Symbolic Method==
Line 741: Line 739:
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
 
|
 
|
−
<math>\begin{array}{lllll}
+
<math>\begin{matrix}
−
F & = & (f, g) & = & ( ~\texttt{((u)(v))}~ , ~\texttt{((u,~v))}~ ).
+
F & = & (f, g) & = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ ).
−
\end{array}</math>
+
\end{matrix}</math>
 
|}
 
|}
  
−
In their application to this logical transformation the operators <math>\operatorname{E}</math> and <math>\operatorname{D}</math> respectively produce the ''enlarged map'' <math>\operatorname{E}F = (\operatorname{E}f, \operatorname{E}g)</math> and the ''difference map'' <math>\operatorname{D}F = (\operatorname{D}f, \operatorname{D}g),</math> whose components can be given as follows, if the reader, in the absence of a special format for logical parentheses, can forgive syntactically bilingual phrases:
+
In their application to this logical transformation the operators <math>\mathrm{E}\!</math> and <math>\mathrm{D}\!</math> respectively produce the ''enlarged map'' <math>\mathrm{E}F = (\mathrm{E}f, \mathrm{E}g)\!</math> and the ''difference map'' <math>\mathrm{D}F = (\mathrm{D}f, \mathrm{D}g),\!</math> whose components can be given as follows.
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
 
|
 
|
 
<math>\begin{array}{lll}
 
<math>\begin{array}{lll}
−
\operatorname{E}f & = & \texttt{(( u + du )( v + dv ))}
+
\mathrm{E}f & = & \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}
−
\\ \\
+
\\[8pt]
−
\operatorname{E}g & = & \texttt{(( u + du ,~ v + dv ))}
+
\mathrm{E}g & = & \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))}
−
\\ \\
+
\\[8pt]
−
\operatorname{D}f & = & \texttt{((u)(v)) ~+~ (( u + du )( v + dv ))}
+
\mathrm{D}f & = & \texttt{((} u \texttt{)(} v \texttt{))} ~+~ \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}
−
\\ \\
+
\\[8pt]
−
\operatorname{D}g & = & \texttt{((u,~v)) ~+~ (( u + du ,~ v + dv ))}
+
\mathrm{D}g & = & \texttt{((} u \texttt{,~} v \texttt{))} ~+~ \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))}
−
\end{array}\!</math>
+
\end{array}</math>
 
|}
 
|}
  
 
But these initial formulas are purely definitional, and help us little to understand either the purpose of the operators or the significance of the results.  Working symbolically, let's apply a more systematic method to the separate components of the mapping <math>F.\!</math>
 
But these initial formulas are purely definitional, and help us little to understand either the purpose of the operators or the significance of the results.  Working symbolically, let's apply a more systematic method to the separate components of the mapping <math>F.\!</math>
  
−
A sketch of this work is presented in the following series of Figures, where each logical proposition is expanded over the basic cells <math>\texttt{uv}, \texttt{u(v)}, \texttt{(u)v}, \texttt{(u)(v)}</math> of the 2-dimensional universe of discourse <math>U^\bullet = [u, v].\!</math>
+
A sketch of this work is presented in the following series of Figures, where each logical proposition is expanded over the basic cells <math>uv, u \texttt{(} v \texttt{)}, \texttt{(} u \texttt{)} v, \texttt{(} u \texttt{)(} v \texttt{)}\!</math> of the 2-dimensional universe of discourse <math>U^\bullet = [u, v].\!</math>
  
 
===Computation Summary : <math>f(u, v) = \texttt{((u)(v))}</math>===
 
===Computation Summary : <math>f(u, v) = \texttt{((u)(v))}</math>===
Line 813: Line 811:
 
|}
 
|}
  
−
Figure&nbsp;1.2 expands <math>\operatorname{E}f = \texttt{((u + du)(v + dv))}</math> over <math>[u, v]\!</math> to give:
+
Figure&nbsp;1.2 expands <math>\mathrm{E}f = \texttt{((u + du)(v + dv))}</math> over <math>[u, v]\!</math> to give:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 863: Line 861:
 
|}
 
|}
  
−
Figure&nbsp;1.3 expands <math>\operatorname{D}f = f + \operatorname{E}f</math> over <math>[u, v]\!</math> to produce:
+
Figure&nbsp;1.3 expands <math>\mathrm{D}f = f + \mathrm{E}f</math> over <math>[u, v]\!</math> to produce:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 963: Line 961:
 
|}
 
|}
  
−
Figure&nbsp;2.2 expands <math>\operatorname{E}g = \texttt{((u + du,~v + dv))}</math> over <math>[u, v]\!</math> to give:
+
Figure&nbsp;2.2 expands <math>\mathrm{E}g = \texttt{((u + du,~v + dv))}</math> over <math>[u, v]\!</math> to give:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 1,013: Line 1,011:
 
|}
 
|}
  
−
Figure&nbsp;2.3 expands <math>\operatorname{D}g = g + \operatorname{E}g</math> over <math>[u, v]\!</math> to yield the form:
+
Figure&nbsp;2.3 expands <math>\mathrm{D}g = g + \mathrm{E}g</math> over <math>[u, v]\!</math> to yield the form:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 1,088: Line 1,086:
 
|}
 
|}
  
−
To speed things along, I will skip a mass of motivating discussion and just exhibit the simplest form of a differential <math>\operatorname{d}F\!</math> for the current example of a logical transformation <math>F,\!</math> after which the majority of the easiest questions will have been answered in visually intuitive terms.
+
To speed things along, I will skip a mass of motivating discussion and just exhibit the simplest form of a differential <math>\mathrm{d}F\!</math> for the current example of a logical transformation <math>F,\!</math> after which the majority of the easiest questions will have been answered in visually intuitive terms.
  
−
For <math>F = (f, g)\!</math> we have <math>\operatorname{d}F = (\operatorname{d}f, \operatorname{d}g),</math> and so we can proceed componentwise, patching the pieces back together at the end.
+
For <math>F = (f, g)\!</math> we have <math>\mathrm{d}F = (\mathrm{d}f, \mathrm{d}g),</math> and so we can proceed componentwise, patching the pieces back together at the end.
  
 
We have prepared the ground already by computing these terms:
 
We have prepared the ground already by computing these terms:
Line 1,097: Line 1,095:
 
|
 
|
 
<math>\begin{array}{lll}
 
<math>\begin{array}{lll}
−
\operatorname{E}f & = & \texttt{(( u + du )( v + dv ))}
+
\mathrm{E}f & = & \texttt{(( u + du )( v + dv ))}
 
\\ \\
 
\\ \\
−
\operatorname{E}g & = & \texttt{(( u + du ,~ v + dv ))}
+
\mathrm{E}g & = & \texttt{(( u + du ,~ v + dv ))}
 
\\ \\
 
\\ \\
−
\operatorname{D}f & = & \texttt{((u)(v)) ~+~ (( u + du )( v + dv ))}
+
\mathrm{D}f & = & \texttt{((u)(v)) ~+~ (( u + du )( v + dv ))}
 
\\ \\
 
\\ \\
−
\operatorname{D}g & = & \texttt{((u,~v)) ~+~ (( u + du ,~ v + dv ))}
+
\mathrm{D}g & = & \texttt{((u,~v)) ~+~ (( u + du ,~ v + dv ))}
 
\end{array}\!</math>
 
\end{array}\!</math>
 
|}
 
|}
  
−
As a matter of fact, computing the symmetric differences <math>\operatorname{D}f = f + \operatorname{E}f</math> and <math>\operatorname{D}g = g + \operatorname{E}g</math> has already taken care of the ''localizing'' part of the task by subtracting out the forms of <math>f\!</math> and <math>g\!</math> from the forms of <math>\operatorname{E}f</math> and <math>\operatorname{E}g,</math> respectively.  Thus all we have left to do is to decide what linear propositions best approximate the difference maps <math>\operatorname{D}f</math> and <math>\operatorname{D}g,</math> respectively.
+
As a matter of fact, computing the symmetric differences <math>\mathrm{D}f = f + \mathrm{E}f</math> and <math>\mathrm{D}g = g + \mathrm{E}g</math> has already taken care of the ''localizing'' part of the task by subtracting out the forms of <math>f\!</math> and <math>g\!</math> from the forms of <math>\mathrm{E}f</math> and <math>\mathrm{E}g,</math> respectively.  Thus all we have left to do is to decide what linear propositions best approximate the difference maps <math>\mathrm{D}f</math> and <math>\mathrm{D}g,</math> respectively.
  
 
This raises the question:  What is a linear proposition?
 
This raises the question:  What is a linear proposition?
Line 1,115: Line 1,113:
 
In particular, the linear functions that we want will be linear functions in the differential variables <math>du\!</math> and <math>dv.\!</math>
 
In particular, the linear functions that we want will be linear functions in the differential variables <math>du\!</math> and <math>dv.\!</math>
  
−
As it turns out, there are just four linear propositions in the associated ''differential universe'' <math>\operatorname{d}U^\bullet = [du, dv],</math> and these are the propositions that are commonly denoted:  <math>\texttt{0}, \texttt{du}, \texttt{dv}, \texttt{du + dv},</math> in other words, <math>\texttt{()}, \texttt{du}, \texttt{dv}, \texttt{(du, dv)}.</math>
+
As it turns out, there are just four linear propositions in the associated ''differential universe'' <math>\mathrm{d}U^\bullet = [du, dv],</math> and these are the propositions that are commonly denoted:  <math>\texttt{0}, \texttt{du}, \texttt{dv}, \texttt{du + dv},</math> in other words, <math>\texttt{()}, \texttt{du}, \texttt{dv}, \texttt{(du, dv)}.</math>
  
 
==Notions of Approximation==
 
==Notions of Approximation==
Line 1,142: Line 1,140:
 
Justifying a notion of approximation is a little more involved in general, and especially in these discrete logical spaces, than it would be expedient for people in a hurry to tangle with right now.  I will just say that there are ''naive'' or ''obvious'' notions and there are ''sophisticated'' or ''subtle'' notions that we might choose among.  The later would engage us in trying to construct proper logical analogues of Lie derivatives, and so let's save that for when we have become subtle or sophisticated or both.  Against or toward that day, as you wish, let's begin with an option in plain view.
 
Justifying a notion of approximation is a little more involved in general, and especially in these discrete logical spaces, than it would be expedient for people in a hurry to tangle with right now.  I will just say that there are ''naive'' or ''obvious'' notions and there are ''sophisticated'' or ''subtle'' notions that we might choose among.  The later would engage us in trying to construct proper logical analogues of Lie derivatives, and so let's save that for when we have become subtle or sophisticated or both.  Against or toward that day, as you wish, let's begin with an option in plain view.
  
−
Figure&nbsp;1.4 illustrates one way of ranging over the cells of the underlying universe <math>U^\bullet = [u, v]\!</math> and selecting at each cell the linear proposition in <math>\operatorname{d}U^\bullet = [du, dv]</math> that best approximates the patch of the difference map <math>\operatorname{D}f</math> that is located there, yielding the following formula for the differential <math>\operatorname{d}f.</math>
+
Figure&nbsp;1.4 illustrates one way of ranging over the cells of the underlying universe <math>U^\bullet = [u, v]\!</math> and selecting at each cell the linear proposition in <math>\mathrm{d}U^\bullet = [du, dv]</math> that best approximates the patch of the difference map <math>\mathrm{D}f</math> that is located there, yielding the following formula for the differential <math>\mathrm{d}f.</math>
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
−
| <math>\operatorname{d}f ~=~ \texttt{uv} \cdot \texttt{0} ~+~ \texttt{u(v)} \cdot \texttt{du} ~+~ \texttt{(u)v} \cdot \texttt{dv} ~+~ \texttt{(u)(v)} \cdot \texttt{(du, dv)}</math>
+
| <math>\mathrm{d}f ~=~ \texttt{uv} \cdot \texttt{0} ~+~ \texttt{u(v)} \cdot \texttt{du} ~+~ \texttt{(u)v} \cdot \texttt{dv} ~+~ \texttt{(u)(v)} \cdot \texttt{(du, dv)}</math>
 
|}
 
|}
  
Line 1,192: Line 1,190:
 
|}
 
|}
  
−
Figure&nbsp;2.4 illustrates one way of ranging over the cells of the underlying universe <math>U^\bullet = [u, v]\!</math> and selecting at each cell the linear proposition in <math>\operatorname{d}U^\bullet = [du, dv]</math> that best approximates the patch of the difference map <math>\operatorname{D}g</math> that is located there, yielding the following formula for the differential <math>\operatorname{d}g.\!</math>
+
Figure&nbsp;2.4 illustrates one way of ranging over the cells of the underlying universe <math>U^\bullet = [u, v]\!</math> and selecting at each cell the linear proposition in <math>\mathrm{d}U^\bullet = [du, dv]</math> that best approximates the patch of the difference map <math>\mathrm{D}g</math> that is located there, yielding the following formula for the differential <math>\mathrm{d}g.\!</math>
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
−
| <math>\operatorname{d}g ~=~ \texttt{uv} \cdot \texttt{(du, dv)} ~+~ \texttt{u(v)} \cdot \texttt{(du, dv)} ~+~ \texttt{(u)v} \cdot \texttt{(du, dv)} ~+~ \texttt{(u)(v)} \cdot \texttt{(du, dv)}</math>
+
| <math>\mathrm{d}g ~=~ \texttt{uv} \cdot \texttt{(du, dv)} ~+~ \texttt{u(v)} \cdot \texttt{(du, dv)} ~+~ \texttt{(u)v} \cdot \texttt{(du, dv)} ~+~ \texttt{(u)(v)} \cdot \texttt{(du, dv)}</math>
 
|}
 
|}
  
Line 1,242: Line 1,240:
 
|}
 
|}
  
−
Well, <math>g,\!</math> that was easy, seeing as how <math>\operatorname{D}g</math> is already linear at each locus, <math>\operatorname{d}g = \operatorname{D}g.</math>
+
Well, <math>g,\!</math> that was easy, seeing as how <math>\mathrm{D}g</math> is already linear at each locus, <math>\mathrm{d}g = \mathrm{D}g.</math>
  
 
==Analytic Series==
 
==Analytic Series==
  
−
We have been conducting the differential analysis of the logical transformation <math>F : [u, v] \mapsto [u, v]</math> defined as <math>F : (u, v) \mapsto ( ~\texttt{((u)(v))}~, ~\texttt{((u, v))}~ ),</math> and this means starting with the extended transformation <math>\operatorname{E}F : [u, v, du, dv] \to [u, v, du, dv]</math> and breaking it into an analytic series, <math>\operatorname{E}F = F + \operatorname{d}F + \operatorname{d}^2 F + \ldots,</math> and
+
We have been conducting the differential analysis of the logical transformation <math>F : [u, v] \mapsto [u, v]</math> defined as <math>F : (u, v) \mapsto ( ~\texttt{((u)(v))}~, ~\texttt{((u, v))}~ ),</math> and this means starting with the extended transformation <math>\mathrm{E}F : [u, v, du, dv] \to [u, v, du, dv]</math> and breaking it into an analytic series, <math>\mathrm{E}F = F + \mathrm{d}F + \mathrm{d}^2 F + \ldots,</math> and
 
so on until there is nothing left to analyze any further.
 
so on until there is nothing left to analyze any further.
  
Line 1,254: Line 1,252:
 
|
 
|
 
<math>\begin{array}{lccccc}
 
<math>\begin{array}{lccccc}
−
1. & \operatorname{E}F    & = & \operatorname{d}^0 F & + & \operatorname{r}^0 F
+
1. & \mathrm{E}F    & = & \mathrm{d}^0 F & + & \mathrm{r}^0 F
 
\\
 
\\
−
2. & \operatorname{r}^0 F & = & \operatorname{d}^1 F & + & \operatorname{r}^1 F
+
2. & \mathrm{r}^0 F & = & \mathrm{d}^1 F & + & \mathrm{r}^1 F
 
\\
 
\\
−
3. & \operatorname{r}^1 F & = & \operatorname{d}^2 F & + & \operatorname{r}^2 F
+
3. & \mathrm{r}^1 F & = & \mathrm{d}^2 F & + & \mathrm{r}^2 F
 
\\
 
\\
 
4. & \ldots
 
4. & \ldots
Line 1,264: Line 1,262:
 
|}
 
|}
  
−
In our analysis of the transformation <math>F,\!</math> we carried out Step&nbsp;1 in the more familiar form <math>\operatorname{E}F = F + \operatorname{D}F,</math> and we have just reached Step&nbsp;2 in the form <math>\operatorname{D}F = \operatorname{d}F + \operatorname{r}F,</math> where <math>\operatorname{r}F</math> is the residual term that remains for us to examine next.
+
In our analysis of the transformation <math>F,\!</math> we carried out Step&nbsp;1 in the more familiar form <math>\mathrm{E}F = F + \mathrm{D}F,</math> and we have just reached Step&nbsp;2 in the form <math>\mathrm{D}F = \mathrm{d}F + \mathrm{r}F,</math> where <math>\mathrm{r}F</math> is the residual term that remains for us to examine next.
  
 
'''NB.'''  I'm am trying to give quick overview here, and this forces me to omit many picky details.  The picky reader may wish to consult the more detailed presentation of this material at the following locations:
 
'''NB.'''  I'm am trying to give quick overview here, and this forces me to omit many picky details.  The picky reader may wish to consult the more detailed presentation of this material at the following locations:
Line 1,290: Line 1,288:
 
|}
 
|}
  
−
Figure&nbsp;1.2 shows the expansion of <math>\operatorname{E}f = \texttt{((u + du)(v + dv))}</math> over <math>[u, v]\!</math> to produce the expression:
+
Figure&nbsp;1.2 shows the expansion of <math>\mathrm{E}f = \texttt{((u + du)(v + dv))}</math> over <math>[u, v]\!</math> to produce the expression:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 1,296: Line 1,294:
 
|}
 
|}
  
−
<math>\operatorname{E}f</math> tells you what you would have to do, from where you are in the universe <math>[u, v],\!</math> if you want to end up in a place where <math>f\!</math> is true.  In this case, where the prevailing proposition <math>f\!</math> is <math>\texttt{((u)(v))},</math> the indication <math>\texttt{uv} \cdot \texttt{(du~dv)}</math> of <math>\operatorname{E}f</math> tells you this:  If <math>u\!</math> and <math>v\!</math> are both true where you are, then just don't change both <math>u\!</math> and <math>v\!</math> at once, and you will end up in a place where <math>\texttt{((u)(v))}</math> is true.
+
<math>\mathrm{E}f</math> tells you what you would have to do, from where you are in the universe <math>[u, v],\!</math> if you want to end up in a place where <math>f\!</math> is true.  In this case, where the prevailing proposition <math>f\!</math> is <math>\texttt{((u)(v))},</math> the indication <math>\texttt{uv} \cdot \texttt{(du~dv)}</math> of <math>\mathrm{E}f</math> tells you this:  If <math>u\!</math> and <math>v\!</math> are both true where you are, then just don't change both <math>u\!</math> and <math>v\!</math> at once, and you will end up in a place where <math>\texttt{((u)(v))}</math> is true.
  
−
Figure&nbsp;1.3 shows the expansion of <math>\operatorname{D}f</math> over <math>[u, v]\!</math> to produce the expression:
+
Figure&nbsp;1.3 shows the expansion of <math>\mathrm{D}f</math> over <math>[u, v]\!</math> to produce the expression:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 1,304: Line 1,302:
 
|}
 
|}
  
−
<math>\operatorname{D}f</math> tells you what you would have to do, from where you are in the universe <math>[u, v],\!</math> if you want to bring about a change in the value of <math>f,\!</math> that is, if you want to get to a place where the value of <math>f\!</math> is different from what it is where you are.  In the present case, where the reigning proposition <math>f\!</math> is <math>\texttt{((u)(v))},</math> the term <math>\texttt{uv} \cdot \texttt{du~dv}</math> of <math>\operatorname{D}f</math> tells you this:  If <math>u\!</math> and <math>v\!</math> are both true where you are, then you would have to change both <math>u\!</math> and <math>v\!</math> in order to reach a place where the value of <math>f\!</math> is different from what it is where you are.
+
<math>\mathrm{D}f</math> tells you what you would have to do, from where you are in the universe <math>[u, v],\!</math> if you want to bring about a change in the value of <math>f,\!</math> that is, if you want to get to a place where the value of <math>f\!</math> is different from what it is where you are.  In the present case, where the reigning proposition <math>f\!</math> is <math>\texttt{((u)(v))},</math> the term <math>\texttt{uv} \cdot \texttt{du~dv}</math> of <math>\mathrm{D}f</math> tells you this:  If <math>u\!</math> and <math>v\!</math> are both true where you are, then you would have to change both <math>u\!</math> and <math>v\!</math> in order to reach a place where the value of <math>f\!</math> is different from what it is where you are.
  
−
Figure&nbsp;1.4 approximates <math>\operatorname{D}f</math> by the linear form <math>\operatorname{d}f</math> that expands over <math>[u, v]\!</math> as follows:
+
Figure&nbsp;1.4 approximates <math>\mathrm{D}f</math> by the linear form <math>\mathrm{d}f</math> that expands over <math>[u, v]\!</math> as follows:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
 
|
 
|
 
<math>\begin{matrix}
 
<math>\begin{matrix}
−
\operatorname{d}f
+
\mathrm{d}f
 
& = & \texttt{uv} \cdot \texttt{0} & + & \texttt{u(v)} \cdot \texttt{du} & + & \texttt{(u)v} \cdot \texttt{dv} & + & \texttt{(u)(v)} \cdot \texttt{(du, dv)}
 
& = & \texttt{uv} \cdot \texttt{0} & + & \texttt{u(v)} \cdot \texttt{du} & + & \texttt{(u)v} \cdot \texttt{dv} & + & \texttt{(u)(v)} \cdot \texttt{(du, dv)}
 
\\ \\
 
\\ \\
Line 1,318: Line 1,316:
 
|}
 
|}
  
−
Figure&nbsp;1.5 shows what remains of the difference map <math>\operatorname{D}f</math> when the first order linear contribution <math>\operatorname{d}f</math> is removed, namely:
+
Figure&nbsp;1.5 shows what remains of the difference map <math>\mathrm{D}f</math> when the first order linear contribution <math>\mathrm{d}f</math> is removed, namely:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
 
|
 
|
 
<math>\begin{matrix}
 
<math>\begin{matrix}
−
\operatorname{r}f
+
\mathrm{r}f
 
& = & \texttt{uv} \cdot \texttt{du~dv} & + & \texttt{u(v)} \cdot \texttt{du~dv} & + & \texttt{(u)v} \cdot \texttt{du~dv} & + & \texttt{(u)(v)} \cdot \texttt{du~dv}
 
& = & \texttt{uv} \cdot \texttt{du~dv} & + & \texttt{u(v)} \cdot \texttt{du~dv} & + & \texttt{(u)v} \cdot \texttt{du~dv} & + & \texttt{(u)(v)} \cdot \texttt{du~dv}
 
\\ \\
 
\\ \\
Line 1,566: Line 1,564:
 
|}
 
|}
  
−
Figure&nbsp;2.2 shows the expansion of <math>\operatorname{E}g = \texttt{((u + du, v + dv))}</math> over <math>[u, v]\!</math> to produce the expression:
+
Figure&nbsp;2.2 shows the expansion of <math>\mathrm{E}g = \texttt{((u + du, v + dv))}</math> over <math>[u, v]\!</math> to produce the expression:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 1,572: Line 1,570:
 
|}
 
|}
  
−
<math>\operatorname{E}g</math> tells you what you would have to do, from where you are in the universe <math>[u, v],\!</math> if you want to end up in a place where <math>g\!</math> is true.  In this case, where the prevailing proposition <math>g\!</math> is <math>\texttt{((u, v))},</math> the component <math>\texttt{uv} \cdot \texttt{((du, dv))}</math> of <math>\operatorname{E}g</math> tells you this:  If <math>u\!</math> and <math>v\!</math> are both true where you are, then change either both or neither of <math>u\!</math> and <math>v\!</math> at the same time, and you will attain a place where <math>\texttt{((du, dv))}</math> is true.
+
<math>\mathrm{E}g</math> tells you what you would have to do, from where you are in the universe <math>[u, v],\!</math> if you want to end up in a place where <math>g\!</math> is true.  In this case, where the prevailing proposition <math>g\!</math> is <math>\texttt{((u, v))},</math> the component <math>\texttt{uv} \cdot \texttt{((du, dv))}</math> of <math>\mathrm{E}g</math> tells you this:  If <math>u\!</math> and <math>v\!</math> are both true where you are, then change either both or neither of <math>u\!</math> and <math>v\!</math> at the same time, and you will attain a place where <math>\texttt{((du, dv))}</math> is true.
  
−
Figure&nbsp;2.3 shows the expansion of <math>\operatorname{D}g</math> over <math>[u, v]\!</math> to produce the expression:
+
Figure&nbsp;2.3 shows the expansion of <math>\mathrm{D}g</math> over <math>[u, v]\!</math> to produce the expression:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 1,580: Line 1,578:
 
|}
 
|}
  
−
<math>\operatorname{D}g</math> tells you what you would have to do, from where you are in the universe <math>[u, v],\!</math> if you want to bring about a change in the value of <math>g,\!</math> that is, if you want to get to a place where the value of <math>g\!</math> is different from what it is where you are.  In the present case, where the ruling proposition <math>g\!</math> is <math>\texttt{((u, v))},</math> the term <math>\texttt{uv} \cdot \texttt{(du, dv)}</math> of <math>\operatorname{D}g</math> tells you this:  If <math>u\!</math> and <math>v\!</math> are both true where you are, then you would have to change one or the other but not both <math>u\!</math> and <math>v\!</math> in order to reach a place where the value of <math>g\!</math> is different from what it is where you are.
+
<math>\mathrm{D}g</math> tells you what you would have to do, from where you are in the universe <math>[u, v],\!</math> if you want to bring about a change in the value of <math>g,\!</math> that is, if you want to get to a place where the value of <math>g\!</math> is different from what it is where you are.  In the present case, where the ruling proposition <math>g\!</math> is <math>\texttt{((u, v))},</math> the term <math>\texttt{uv} \cdot \texttt{(du, dv)}</math> of <math>\mathrm{D}g</math> tells you this:  If <math>u\!</math> and <math>v\!</math> are both true where you are, then you would have to change one or the other but not both <math>u\!</math> and <math>v\!</math> in order to reach a place where the value of <math>g\!</math> is different from what it is where you are.
  
−
Figure&nbsp;2.4 approximates <math>\operatorname{D}g</math> by the linear form <math>\operatorname{d}g</math> that expands over <math>[u, v]\!</math> as follows:
+
Figure&nbsp;2.4 approximates <math>\mathrm{D}g</math> by the linear form <math>\mathrm{d}g</math> that expands over <math>[u, v]\!</math> as follows:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
 
|
 
|
 
<math>\begin{array}{lll}
 
<math>\begin{array}{lll}
−
\operatorname{d}g
+
\mathrm{d}g
 
& = & \texttt{uv}\!\cdot\!\texttt{(du, dv)} + \texttt{u(v)}\!\cdot\!\texttt{(du, dv)} + \texttt{(u)v}\!\cdot\!\texttt{(du, dv)} + \texttt{(u)(v)}\!\cdot\!\texttt{(du, dv)}
 
& = & \texttt{uv}\!\cdot\!\texttt{(du, dv)} + \texttt{u(v)}\!\cdot\!\texttt{(du, dv)} + \texttt{(u)v}\!\cdot\!\texttt{(du, dv)} + \texttt{(u)(v)}\!\cdot\!\texttt{(du, dv)}
 
\\ \\
 
\\ \\
Line 1,594: Line 1,592:
 
|}
 
|}
  
−
Figure&nbsp;2.5 shows what remains of the difference map <math>\operatorname{D}g</math> when the first order linear contribution <math>\operatorname{d}g</math> is removed, namely:
+
Figure&nbsp;2.5 shows what remains of the difference map <math>\mathrm{D}g</math> when the first order linear contribution <math>\mathrm{d}g</math> is removed, namely:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
 
|
 
|
 
<math>\begin{matrix}
 
<math>\begin{matrix}
−
\operatorname{r}g
+
\mathrm{r}g
 
& = & \texttt{uv} \cdot \texttt{0} & + & \texttt{u(v)} \cdot \texttt{0} & + & \texttt{(u)v} \cdot \texttt{0} & + & \texttt{(u)(v)} \cdot \texttt{0}
 
& = & \texttt{uv} \cdot \texttt{0} & + & \texttt{u(v)} \cdot \texttt{0} & + & \texttt{(u)v} \cdot \texttt{0} & + & \texttt{(u)(v)} \cdot \texttt{0}
 
\\ \\
 
\\ \\
Line 1,881: Line 1,879:
 
By way of providing a simple illustration of Cook's Theorem, namely, that &ldquo;Propositional Satisfiability is NP-Complete&rdquo;, I will describe one way to translate finite approximations of turing machines into propositional expressions, using the cactus language syntax for propositional calculus that I will describe in more detail as we proceed.
 
By way of providing a simple illustration of Cook's Theorem, namely, that &ldquo;Propositional Satisfiability is NP-Complete&rdquo;, I will describe one way to translate finite approximations of turing machines into propositional expressions, using the cactus language syntax for propositional calculus that I will describe in more detail as we proceed.
  
−
:; <math>\operatorname{Stilt}(k) =\!</math>
+
:; <math>\mathrm{Stilt}(k) =\!</math>
 
:: '''Space and time limited turing machine''',
 
:: '''Space and time limited turing machine''',
 
:: with <math>k\!</math> units of space and <math>k\!</math> units of time.
 
:: with <math>k\!</math> units of space and <math>k\!</math> units of time.
  
−
:; <math>\operatorname{Stunt}(k) =\!</math>
+
:; <math>\mathrm{Stunt}(k) =\!</math>
 
:: '''Space and time limited turing machine''',
 
:: '''Space and time limited turing machine''',
 
:: for computing the parity of a bit string, with number of tape cells of input equal to <math>k.\!</math>
 
:: for computing the parity of a bit string, with number of tape cells of input equal to <math>k.\!</math>
Line 1,938: Line 1,936:
 
<br>
 
<br>
  
−
The TM has a ''finite automaton'' (FA) as one component.  Let us refer to this particular FA by the name of <math>\operatorname{M}.</math>
+
The TM has a ''finite automaton'' (FA) as one component.  Let us refer to this particular FA by the name of <math>\mathrm{M}.</math>
  
−
The ''tape head'' (that is, the ''read unit'') will be called <math>\operatorname{H}.</math>  The ''registers'' are also called ''tape cells'' or ''tape squares''.
+
The ''tape head'' (that is, the ''read unit'') will be called <math>\mathrm{H}.</math>  The ''registers'' are also called ''tape cells'' or ''tape squares''.
  
 
===Finite Approximations===
 
===Finite Approximations===
  
−
To see how each finite approximation to a given turing machine can be given a purely propositional description, one fixes the parameter <math>k\!</math> and limits the rest of the discussion to describing <math>\operatorname{Stilt}(k),\!</math> which is not really a full-fledged TM anymore but just a finite automaton in disguise.
+
To see how each finite approximation to a given turing machine can be given a purely propositional description, one fixes the parameter <math>k\!</math> and limits the rest of the discussion to describing <math>\mathrm{Stilt}(k),\!</math> which is not really a full-fledged TM anymore but just a finite automaton in disguise.
  
−
In this example, for the sake of a minimal illustration, we choose <math>k = 2,\!</math> and discuss <math>\operatorname{Stunt}(2).</math>  Since the zeroth tape cell and the last tape cell are both occupied by the character <math>^{\backprime\backprime}\texttt{\#}^{\prime\prime}</math> that is used for both the ''beginning of file'' <math>(\operatorname{bof})</math> and the ''end of file'' <math>(\operatorname{eof})</math> markers, this allows for only one digit of significant computation.
+
In this example, for the sake of a minimal illustration, we choose <math>k = 2,\!</math> and discuss <math>\mathrm{Stunt}(2).</math>  Since the zeroth tape cell and the last tape cell are both occupied by the character <math>^{\backprime\backprime}\texttt{\#}^{\prime\prime}</math> that is used for both the ''beginning of file'' <math>(\mathrm{bof})</math> and the ''end of file'' <math>(\mathrm{eof})</math> markers, this allows for only one digit of significant computation.
  
−
To translate <math>\operatorname{Stunt}(2)</math> into propositional form we use the following collection of basic propositions, boolean variables, or logical features, depending on what one prefers to call them:
+
To translate <math>\mathrm{Stunt}(2)</math> into propositional form we use the following collection of basic propositions, boolean variables, or logical features, depending on what one prefers to call them:
  
−
The basic propositions for describing the ''present state function'' <math>\operatorname{QF} : P \to Q</math> are these:
+
The basic propositions for describing the ''present state function'' <math>\mathrm{QF} : P \to Q</math> are these:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 1,968: Line 1,966:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
−
| At the point-in-time <math>p_i,\!</math> the finite state machine <math>\operatorname{M}</math> is in the state <math>q_j.\!</math>
+
| At the point-in-time <math>p_i,\!</math> the finite state machine <math>\mathrm{M}</math> is in the state <math>q_j.\!</math>
 
|}
 
|}
  
−
The basic propositions for describing the ''present register function'' <math>\operatorname{RF} : P \to R</math> are these:
+
The basic propositions for describing the ''present register function'' <math>\mathrm{RF} : P \to R</math> are these:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 1,989: Line 1,987:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
−
| At the point-in-time <math>p_i,\!</math> the tape head <math>\operatorname{H}</math> is on the tape cell <math>r_j.\!</math>
+
| At the point-in-time <math>p_i,\!</math> the tape head <math>\mathrm{H}</math> is on the tape cell <math>r_j.\!</math>
 
|}
 
|}
  
−
The basic propositions for describing the ''present symbol function'' <math>\operatorname{SF} : P \to (R \to S)</math> are these:
+
The basic propositions for describing the ''present symbol function'' <math>\mathrm{SF} : P \to (R \to S)</math> are these:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 2,039: Line 2,037:
 
===Initial Conditions===
 
===Initial Conditions===
  
−
Given but a single free square on the tape, there are just two different sets of initial conditions for <math>\operatorname{Stunt}(2),</math> the finite approximation to the parity turing machine that we are presently considering.
+
Given but a single free square on the tape, there are just two different sets of initial conditions for <math>\mathrm{Stunt}(2),</math> the finite approximation to the parity turing machine that we are presently considering.
  
 
====Initial Conditions for Tape Input "0"====
 
====Initial Conditions for Tape Input "0"====
  
−
The following conjunction of 5 basic propositions describes the initial conditions when <math>\operatorname{Stunt}(2)</math> is started with an input of "0" in its free square:
+
The following conjunction of 5 basic propositions describes the initial conditions when <math>\mathrm{Stunt}(2)</math> is started with an input of "0" in its free square:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 2,064: Line 2,062:
 
{| align="center" cellpadding=8" width="90%"
 
{| align="center" cellpadding=8" width="90%"
 
|
 
|
−
<p>At time <math>p_0,\!</math> machine <math>\operatorname{M}</math> is in the state <math>q_0,\!</math></p>
+
<p>At time <math>p_0,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math></p>
−
<p>At time <math>p_0,\!</math> scanner <math>\operatorname{H}</math> is reading cell <math>r_1,\!</math></p>
+
<p>At time <math>p_0,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math></p>
 
<p>At time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math></p>
 
<p>At time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math></p>
 
<p>At time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math></p>
 
<p>At time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math></p>
Line 2,073: Line 2,071:
 
====Initial Conditions for Tape Input "1"====
 
====Initial Conditions for Tape Input "1"====
  
−
The following conjunction of 5 basic propositions describes the initial conditions when <math>\operatorname{Stunt}(2)</math> is started with an input of "1" in its free square:
+
The following conjunction of 5 basic propositions describes the initial conditions when <math>\mathrm{Stunt}(2)</math> is started with an input of "1" in its free square:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 2,094: Line 2,092:
 
{| align="center" cellpadding=8" width="90%"
 
{| align="center" cellpadding=8" width="90%"
 
|
 
|
−
<p>At time <math>p_0,\!</math> machine <math>\operatorname{M}</math> is in the state <math>q_0,\!</math></p>
+
<p>At time <math>p_0,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math></p>
−
<p>At time <math>p_0,\!</math> scanner <math>\operatorname{H}</math> is reading cell <math>r_1,\!</math></p>
+
<p>At time <math>p_0,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math></p>
 
<p>At time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math></p>
 
<p>At time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math></p>
 
<p>At time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math></p>
 
<p>At time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math></p>
Line 2,103: Line 2,101:
 
===Propositional Program===
 
===Propositional Program===
  
−
A complete description of <math>\operatorname{Stunt}(2)</math> in propositional form is obtained by conjoining one of the above choices for initial conditions with all of the following sets of propositions, that serve in effect as a simple type of ''declarative program'', telling us all that we need to know about the anatomy and behavior of the truncated TM in question.
+
A complete description of <math>\mathrm{Stunt}(2)</math> in propositional form is obtained by conjoining one of the above choices for initial conditions with all of the following sets of propositions, that serve in effect as a simple type of ''declarative program'', telling us all that we need to know about the anatomy and behavior of the truncated TM in question.
  
 
====Mediate Conditions====
 
====Mediate Conditions====
Line 2,264: Line 2,262:
 
===Interpretation of the Propositional Program===
 
===Interpretation of the Propositional Program===
  
−
Let us now run through the propositional specification of <math>\operatorname{Stunt}(2),</math> our truncated TM, and paraphrase what it says in ordinary language.
+
Let us now run through the propositional specification of <math>\mathrm{Stunt}(2),</math> our truncated TM, and paraphrase what it says in ordinary language.
  
 
====Mediate Conditions====
 
====Mediate Conditions====
Line 2,286: Line 2,284:
 
|
 
|
 
<math>\begin{array}{l}
 
<math>\begin{array}{l}
−
\operatorname{not}~ p ~\operatorname{without}~ q
+
\mathrm{not}~ p ~\mathrm{without}~ q
 
\\[4pt]
 
\\[4pt]
−
p ~\operatorname{implies}~ q
+
p ~\mathrm{implies}~ q
 
\\[4pt]
 
\\[4pt]
−
\operatorname{if}~ p ~\operatorname{then}~ q
+
\mathrm{if}~ p ~\mathrm{then}~ q
 
\\[4pt]
 
\\[4pt]
 
p \Rightarrow q
 
p \Rightarrow q
Line 2,322: Line 2,320:
 
{| align="center" cellpadding=8" width="90%"
 
{| align="center" cellpadding=8" width="90%"
 
|
 
|
−
<p>If <math>\operatorname{M}</math> at <math>p_0\!</math> is in state <math>q_\#,\!</math> then <math>\operatorname{M}</math> at <math>p_1\!</math> is in state <math>q_\#,\!</math> and</p>
+
<p>If <math>\mathrm{M}</math> at <math>p_0\!</math> is in state <math>q_\#,\!</math> then <math>\mathrm{M}</math> at <math>p_1\!</math> is in state <math>q_\#,\!</math> and</p>
  
−
<p>If <math>\operatorname{M}</math> at <math>p_0\!</math> is in state <math>q_*,\!</math> then <math>\operatorname{M}</math> at <math>p_1\!</math> is in state <math>q_*,\!</math> and</p>
+
<p>If <math>\mathrm{M}</math> at <math>p_0\!</math> is in state <math>q_*,\!</math> then <math>\mathrm{M}</math> at <math>p_1\!</math> is in state <math>q_*,\!</math> and</p>
  
−
<p>If <math>\operatorname{M}</math> at <math>p_1\!</math> is in state <math>q_\#,\!</math> then <math>\operatorname{M}</math> at <math>p_2\!</math> is in state <math>q_\#,\!</math> and</p>
+
<p>If <math>\mathrm{M}</math> at <math>p_1\!</math> is in state <math>q_\#,\!</math> then <math>\mathrm{M}</math> at <math>p_2\!</math> is in state <math>q_\#,\!</math> and</p>
  
−
<p>If <math>\operatorname{M}</math> at <math>p_1\!</math> is in state <math>q_*,\!</math> then <math>\operatorname{M}</math> at <math>p_2\!</math> is in state <math>q_*.\!</math></p>
+
<p>If <math>\mathrm{M}</math> at <math>p_1\!</math> is in state <math>q_*,\!</math> then <math>\mathrm{M}</math> at <math>p_2\!</math> is in state <math>q_*.\!</math></p>
 
|}
 
|}
  
Line 2,340: Line 2,338:
 
|}
 
|}
  
−
In cactus syntax, an expression of the form <math>\texttt{((p)(q))}</math> expresses the disjunction <math>p ~\operatorname{or}~ q.</math>  The corresponding cactus graph, here just a tree, has the following shape:
+
In cactus syntax, an expression of the form <math>\texttt{((p)(q))}</math> expresses the disjunction <math>p ~\mathrm{or}~ q.</math>  The corresponding cactus graph, here just a tree, has the following shape:
  
 
<br>
 
<br>
Line 2,368: Line 2,366:
 
{| align="center" cellpadding=8" width="90%"
 
{| align="center" cellpadding=8" width="90%"
 
|
 
|
−
<p>At time <math>p_2\!</math> machine <math>\operatorname{M}</math> is in state <math>q_\#,\!</math> or</p>
+
<p>At time <math>p_2\!</math> machine <math>\mathrm{M}</math> is in state <math>q_\#,\!</math> or</p>
−
<p>At time <math>p_2\!</math> machine <math>\operatorname{M}</math> is in state <math>q_*.\!</math></p>
+
<p>At time <math>p_2\!</math> machine <math>\mathrm{M}</math> is in state <math>q_*.\!</math></p>
 
|}
 
|}
  
Line 2,416: Line 2,414:
 
<br>
 
<br>
  
−
The State Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction expressing the condition that <math>\operatorname{M}</math> has to be in one and only one of its states at each point in time under consideration.  In short, we have the constraint:
+
The State Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction expressing the condition that <math>\mathrm{M}</math> has to be in one and only one of its states at each point in time under consideration.  In short, we have the constraint:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 2,422: Line 2,420:
 
<p>At each of the points in time <math>p_i,\!</math> for <math>i\!</math> in the set <math>\{ 0, 1, 2 \},\!</math></p>
 
<p>At each of the points in time <math>p_i,\!</math> for <math>i\!</math> in the set <math>\{ 0, 1, 2 \},\!</math></p>
  
−
<p><math>\operatorname{M}</math> can be in exactly one state <math>q_j,\!</math> for <math>j\!</math> in the set <math>\{ 0, 1, \#, * \}.\!</math></p>
+
<p><math>\mathrm{M}</math> can be in exactly one state <math>q_j,\!</math> for <math>j\!</math> in the set <math>\{ 0, 1, \#, * \}.\!</math></p>
 
|}
 
|}
  
Line 2,438: Line 2,436:
 
|}
 
|}
  
−
The Register Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction saying that the read head <math>\operatorname{H}</math> must be reading one and only one of the registers or tape cells available to it at each of the points in time under consideration.  In sum:
+
The Register Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction saying that the read head <math>\mathrm{H}</math> must be reading one and only one of the registers or tape cells available to it at each of the points in time under consideration.  In sum:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 2,444: Line 2,442:
 
<p>At each of the points in time <math>p_i,\!</math> for <math>i = 0, 1, 2,\!</math></p>
 
<p>At each of the points in time <math>p_i,\!</math> for <math>i = 0, 1, 2,\!</math></p>
  
−
<p><math>\operatorname{H}</math> is reading exactly one cell <math>r_j,\!</math> for <math>j = 0, 1, 2.\!</math>
+
<p><math>\mathrm{H}</math> is reading exactly one cell <math>r_j,\!</math> for <math>j = 0, 1, 2.\!</math>
 
|}
 
|}
  
Line 2,472: Line 2,470:
 
|}
 
|}
  
−
The Symbol Partition segment of the propositional program for <math>\operatorname{Stunt}(2)</math> consists of nine universal partition expressions, taken in conjunction stipulating that there has to be one and only one symbol in each of the registers at each point in time under consideration.  In short, we have:
+
The Symbol Partition segment of the propositional program for <math>\mathrm{Stunt}(2)</math> consists of nine universal partition expressions, taken in conjunction stipulating that there has to be one and only one symbol in each of the registers at each point in time under consideration.  In short, we have:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
Line 2,558: Line 2,556:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
−
|<math>\operatorname{If}</math>
+
|<math>\mathrm{If}</math>
 
|-
 
|-
 
| At the time <math>p_i,\!</math> the tape cell <math>r_j\!</math> bears the mark <math>s_k,\!</math>
 
| At the time <math>p_i,\!</math> the tape cell <math>r_j\!</math> bears the mark <math>s_k,\!</math>
 
|-
 
|-
−
| <math>\operatorname{But}</math> it is not the case that:
+
| <math>\mathrm{But}</math> it is not the case that:
 
|-
 
|-
 
| At the time <math>p_i,\!</math> the tape head is on the tape cell <math>r_j,\!</math>
 
| At the time <math>p_i,\!</math> the tape head is on the tape cell <math>r_j,\!</math>
 
|-
 
|-
−
| <math>\operatorname{Then}</math>
+
| <math>\mathrm{Then}</math>
 
|-
 
|-
 
| At the time <math>p_{i+1},\!</math> the tape cell <math>r_j\!</math> bears the mark <math>s_k.\!</math>
 
| At the time <math>p_{i+1},\!</math> the tape cell <math>r_j\!</math> bears the mark <math>s_k.\!</math>
Line 2,612: Line 2,610:
 
|}
 
|}
  
−
The Transition Relation segment of the propositional program for <math>\operatorname{Stunt}(2)</math> consists of sixteen implication statements with complex antecedents and consequents.  Taken together, these give propositional expression to the TM Figure and Table that were given at the outset.
+
The Transition Relation segment of the propositional program for <math>\mathrm{Stunt}(2)</math> consists of sixteen implication statements with complex antecedents and consequents.  Taken together, these give propositional expression to the TM Figure and Table that were given at the outset.
  
 
Just by way of a single example, consider the clause:
 
Just by way of a single example, consider the clause:
Line 2,623: Line 2,621:
  
 
{| align="center" cellpadding="8" width="90%"
 
{| align="center" cellpadding="8" width="90%"
−
|<math>\operatorname{If}</math>
+
|<math>\mathrm{If}</math>
 
|-
 
|-
−
| At the time <math>p_0,\!</math> the machine <math>\operatorname{M}</math> is in the state <math>q_0,\!</math> and
+
| At the time <math>p_0,\!</math> the machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math> and
 
|-
 
|-
−
| At the time <math>p_0,\!</math> the scanner <math>\operatorname{H}</math> is reading cell <math>r_1,\!</math> and
+
| At the time <math>p_0,\!</math> the scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math> and
 
|-
 
|-
 
| At the time <math>p_0,\!</math> the tape cell <math>r_1\!</math> contains a <math>\texttt{1},</math>
 
| At the time <math>p_0,\!</math> the tape cell <math>r_1\!</math> contains a <math>\texttt{1},</math>
 
|-
 
|-
−
| <math>\operatorname{Then}</math>
+
| <math>\mathrm{Then}</math>
 
|-
 
|-
−
| At the time <math>p_1,\!</math> the machine <math>\operatorname{M}</math> is in the state <math>q_1,\!</math> and
+
| At the time <math>p_1,\!</math> the machine <math>\mathrm{M}</math> is in the state <math>q_1,\!</math> and
 
|-
 
|-
−
| At the time <math>p_1,\!</math> the scanner <math>\operatorname{H}</math> is reading cell <math>r_2,\!</math> and
+
| At the time <math>p_1,\!</math> the scanner <math>\mathrm{H}</math> is reading cell <math>r_2,\!</math> and
 
|-
 
|-
 
| At the time <math>p_1,\!</math> the tape cell <math>r_1\!</math> contains a <math>\texttt{1}.</math>
 
| At the time <math>p_1,\!</math> the tape cell <math>r_1\!</math> contains a <math>\texttt{1}.</math>
Line 2,642: Line 2,640:
 
===Computation===
 
===Computation===
  
−
The propositional program for <math>\operatorname{Stunt}(2)</math> uses the following set
+
The propositional program for <math>\mathrm{Stunt}(2)</math> uses the following set
 
of <math>9 + 12 + 36 = 57\!</math> basic propositions or boolean variables:
 
of <math>9 + 12 + 36 = 57\!</math> basic propositions or boolean variables:
  
Line 2,698: Line 2,696:
 
===Output===
 
===Output===
  
−
One component of the <math>\begin{smallmatrix}\operatorname{Theme~One}\end{smallmatrix}</math> program that I wrote some years ago finds all the satisfying interpretations of propositions expressed in cactus syntax.  It's not a polynomial time algorithm, as you may guess, but it was just barely efficient enough to do this example in the 500 K of spare memory that I had on an old 286 PC in about 1989, so I will give you the actual outputs from those trials.
+
One component of the <math>\begin{smallmatrix}\mathrm{Theme~One}\end{smallmatrix}</math> program that I wrote some years ago finds all the satisfying interpretations of propositions expressed in cactus syntax.  It's not a polynomial time algorithm, as you may guess, but it was just barely efficient enough to do this example in the 500 K of spare memory that I had on an old 286 PC in about 1989, so I will give you the actual outputs from those trials.
  
 
====Output Conditions for Tape Input "0"====
 
====Output Conditions for Tape Input "0"====
  
−
Let <math>p_0\!</math> be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "0" with the proposition that describes the truncated turing machine <math>\operatorname{Stunt}(2).</math>  As it turns out, <math>p_0\!</math> has a single satisfying interpretation.  This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display:
+
Let <math>p_0\!</math> be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "0" with the proposition that describes the truncated turing machine <math>\mathrm{Stunt}(2).</math>  As it turns out, <math>p_0\!</math> has a single satisfying interpretation.  This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display:
  
 
<br>
 
<br>
Line 2,737: Line 2,735:
 
{| align="center" cellpadding=8" width="90%"
 
{| align="center" cellpadding=8" width="90%"
 
|
 
|
−
<p>At the time <math>p_0,\!</math> machine <math>\operatorname{M}</math> is in the state <math>q_0,\!</math> and</p>
+
<p>At the time <math>p_0,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math> and</p>
−
<p>At the time <math>p_0,\!</math> scanner <math>\operatorname{H}</math> is reading cell <math>r_1,\!</math> and</p>
+
<p>At the time <math>p_0,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math> and</p>
 
<p>At the time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math> and</p>
 
<p>At the time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math> and</p>
Line 2,744: Line 2,742:
 
|-
 
|-
 
|
 
|
−
<p>At the time <math>p_1,\!</math> machine <math>\operatorname{M}</math> is in the state <math>q_0,\!</math> and</p>
+
<p>At the time <math>p_1,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math> and</p>
−
<p>At the time <math>p_1,\!</math> scanner <math>\operatorname{H}</math> is reading cell <math>r_2,\!</math> and</p>
+
<p>At the time <math>p_1,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_2,\!</math> and</p>
 
<p>At the time <math>p_1,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_1,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_1,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math> and</p>
 
<p>At the time <math>p_1,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math> and</p>
Line 2,751: Line 2,749:
 
|-
 
|-
 
|
 
|
−
<p>At the time <math>p_2,\!</math> machine <math>\operatorname{M}</math> is in the state <math>q_\#,\!</math> and</p>
+
<p>At the time <math>p_2,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_\#,\!</math> and</p>
−
<p>At the time <math>p_2,\!</math> scanner <math>\operatorname{H}</math> is reading cell <math>r_1,\!</math> and</p>
+
<p>At the time <math>p_2,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math> and</p>
 
<p>At the time <math>p_2,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_2,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_2,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math> and</p>
 
<p>At the time <math>p_2,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{0},</math> and</p>
Line 2,758: Line 2,756:
 
|}
 
|}
  
−
The output of <math>\operatorname{Stunt}(2)</math> being the symbol that rests under the tape head <math>\operatorname{H}</math> if and when the machine <math>\operatorname{M}</math> reaches one of its resting states, we get the result that <math>\operatorname{Parity}(0) = 0.</math>
+
The output of <math>\mathrm{Stunt}(2)</math> being the symbol that rests under the tape head <math>\mathrm{H}</math> if and when the machine <math>\mathrm{M}</math> reaches one of its resting states, we get the result that <math>\mathrm{Parity}(0) = 0.</math>
  
 
====Output Conditions for Tape Input "1"====
 
====Output Conditions for Tape Input "1"====
  
−
Let <math>p_1\!</math> be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "1" with the proposition that describes the truncated turing machine <math>\operatorname{Stunt}(2).</math>  As it turns out, <math>p_1\!</math> has a single satisfying interpretation.  This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display:
+
Let <math>p_1\!</math> be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "1" with the proposition that describes the truncated turing machine <math>\mathrm{Stunt}(2).</math>  As it turns out, <math>p_1\!</math> has a single satisfying interpretation.  This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display:
  
 
<br>
 
<br>
Line 2,797: Line 2,795:
 
{| align="center" cellpadding=8" width="90%"
 
{| align="center" cellpadding=8" width="90%"
 
|
 
|
−
<p>At the time <math>p_0,\!</math> machine <math>\operatorname{M}</math> is in the state <math>q_0,\!</math> and</p>
+
<p>At the time <math>p_0,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_0,\!</math> and</p>
−
<p>At the time <math>p_0,\!</math> scanner <math>\operatorname{H}</math> is reading cell <math>r_1,\!</math> and</p>
+
<p>At the time <math>p_0,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math> and</p>
 
<p>At the time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_0,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math> and</p>
 
<p>At the time <math>p_0,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math> and</p>
Line 2,804: Line 2,802:
 
|-
 
|-
 
|
 
|
−
<p>At the time <math>p_1,\!</math> machine <math>\operatorname{M}</math> is in the state <math>q_1,\!</math> and</p>
+
<p>At the time <math>p_1,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_1,\!</math> and</p>
−
<p>At the time <math>p_1,\!</math> scanner <math>\operatorname{H}</math> is reading cell <math>r_2,\!</math> and</p>
+
<p>At the time <math>p_1,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_2,\!</math> and</p>
 
<p>At the time <math>p_1,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_1,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_1,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math> and</p>
 
<p>At the time <math>p_1,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math> and</p>
Line 2,811: Line 2,809:
 
|-
 
|-
 
|
 
|
−
<p>At the time <math>p_2,\!</math> machine <math>\operatorname{M}</math> is in the state <math>q_*,\!</math> and</p>
+
<p>At the time <math>p_2,\!</math> machine <math>\mathrm{M}</math> is in the state <math>q_*,\!</math> and</p>
−
<p>At the time <math>p_2,\!</math> scanner <math>\operatorname{H}</math> is reading cell <math>r_1,\!</math> and</p>
+
<p>At the time <math>p_2,\!</math> scanner <math>\mathrm{H}</math> is reading cell <math>r_1,\!</math> and</p>
 
<p>At the time <math>p_2,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_2,\!</math> cell <math>r_0\!</math> contains the symbol <math>\texttt{\#},</math> and</p>
 
<p>At the time <math>p_2,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math> and</p>
 
<p>At the time <math>p_2,\!</math> cell <math>r_1\!</math> contains the symbol <math>\texttt{1},</math> and</p>
Line 2,818: Line 2,816:
 
|}
 
|}
  
−
The output of <math>\operatorname{Stunt}(2)</math> being the symbol that rests under the tape head <math>\operatorname{H}</math> when and if the machine <math>\operatorname{M}</math> reaches one of its resting states, we get the result that <math>\operatorname{Parity}(1) = 1.</math>
+
The output of <math>\mathrm{Stunt}(2)</math> being the symbol that rests under the tape head <math>\mathrm{H}</math> when and if the machine <math>\mathrm{M}</math> reaches one of its resting states, we get the result that <math>\mathrm{Parity}(1) = 1.</math>
  
 
==Work Area==
 
==Work Area==

Revision as of 03:30, 27 September 2013

Author: Jon Awbrey

The task ahead is to chart a course from general ideas about transformational equivalence classes of graphs to a notion of differential analytic turing automata (DATA). It may be a while before we get within sight of that goal, but it will provide a better measure of motivation to name the thread after the envisioned end rather than the more homely starting place.

The basic idea is as follows. One has a set \(\mathcal{G}\) of graphs and a set \(\mathcal{T}\) of transformation rules, and each rule \(\mathrm{t} \in \mathcal{T}\) has the effect of transforming graphs into graphs, \(\mathrm{t} : \mathcal{G} \to \mathcal{G}.\) In the cases that we shall be studying, this set of transformation rules partitions the set of graphs into transformational equivalence classes (TECs).

There are many interesting excursions to be had here, but I will focus mainly on logical applications, and and so the TECs I talk about will almost always have the character of logical equivalence classes (LECs).

An example that will figure heavily in the sequel is given by rooted trees as the species of graphs and a pair of equational transformation rules that derive from the graphical calculi of C.S. Peirce, as revived and extended by George Spencer Brown.

Here are the fundamental transformation rules, also referred to as the arithmetic axioms, more precisely, the arithmetic initials.

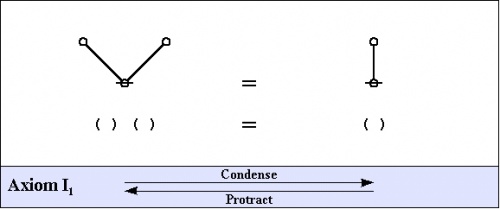PERS Figure 01.jpg (1)
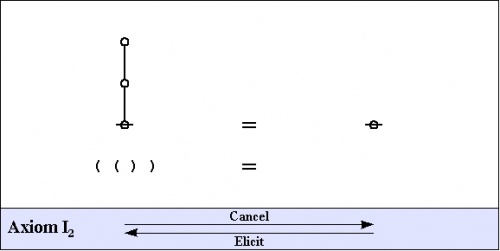PERS Figure 02.jpg (2)

That should be enough to get started.

Cactus Language

I will be making use of the cactus language extension of Peirce's Alpha Graphs, so called because it uses a species of graphs that are usually called "cacti" in graph theory. The last exposition of the cactus syntax that I've written can be found here:

The representational and computational efficiency of the cactus language for the tasks that are usually associated with boolean algebra and propositional calculus makes it possible to entertain a further extension, to what we may call differential logic, because it develops this basic level of logic in the same way that differential calculus augments analytic geometry to handle change and diversity. There are several different introductions to differential logic that I have written and distributed across the Internet. You might start with the following couple of treatments:

I will draw on those previously advertised resources of notation and theory as needed, but right now I sense the need for some concrete examples.

Example 1

Let's say we have a system that is known by the name of its state space \(X\!\) and we have a boolean state variable \(x : X \to \mathbb{B},\!\) where \(\mathbb{B} = \{ 0, 1 \}.\!\)

We observe \(X\!\) for a while, relative to a discrete time frame, and we write down the following sequence of values for \(x.\!\)

\(\begin{array}{c|c} t & x \'"`UNIQ-MathJax1-QINU`"'=== The venn diagram in Figure 1.1 shows how the proposition \(f = \texttt{((u)(v))}\) can be expanded over the universe of discourse \([u, v]\!\) to produce a logically equivalent exclusive disjunction, namely, \(\texttt{uv~+~u(v)~+~(u)v}.\) 

o---------------------------------------o
|                                       |
|                   o                   |
|                  /%\                  |
|                 /%%%\                 |
|                /%%%%%\                |
|               o%%%%%%%o               |
|              /%\%%%%%/%\              |
|             /%%%\%%%/%%%\             |
|            /%%%%%\%/%%%%%\            |
|           o%%%%%%%o%%%%%%%o           |
|          /%\%%%%%/%\%%%%%/%\          |
|         /%%%\%%%/%%%\%%%/%%%\         |
|        /%%%%%\%/%%%%%\%/%%%%%\        |
|       o%%%%%%%o%%%%%%%o%%%%%%%o       |
|      /%\%%%%%/%\%%%%%/%\%%%%%/%\      |
|     /%%%\%%%/%%%\%%%/%%%\%%%/%%%\     |
|    /%%%%%\%/%%%%%\%/%%%%%\%/%%%%%\    |
|   o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o   |
|   |\%%%%%/%\%%%%%/ \%%%%%/%\%%%%%/|   |
|   | \%%%/%%%\%%%/   \%%%/%%%\%%%/ |   |
|   |  \%/%%%%%\%/     \%/%%%%%\%/  |   |
|   |   o%%%%%%%o       o%%%%%%%o   |   |
|   |   |\%%%%%/ \     / \%%%%%/|   |   |
|   |   | \%%%/   \   /   \%%%/ |   |   |
|   | u |  \%/     \ /     \%/  | v |   |
|   o---+---o       o       o---+---o   |
|       |    \     / \     /    |       |
|       |     \   /   \   /     |       |
|       | du   \ /     \ /   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 1.1.  f = ((u)(v))

Figure 1.2 expands \(\mathrm{E}f = \texttt{((u + du)(v + dv))}\) over \([u, v]\!\) to give:

\(\texttt{uv~(du~dv) ~+~ u(v)~(du (dv)) ~+~ (u)v~((du) dv) ~+~ (u)(v)~((du)(dv))}\) 
o---------------------------------------o
|                                       |
|                   o                   |
|                  /%\                  |
|                 /%%%\                 |
|                /%%%%%\                |
|               o%%%%%%%o               |
|              /%\%%%%%/%\              |
|             /%%%\%%%/%%%\             |
|            /%%%%%\%/%%%%%\            |
|           o%%%%%%%o%%%%%%%o           |
|          /%\%%%%%/ \%%%%%/%\          |
|         /%%%\%%%/   \%%%/%%%\         |
|        /%%%%%\%/     \%/%%%%%\        |
|       o%%%%%%%o       o%%%%%%%o       |
|      /%\%%%%%/%\     /%\%%%%%/%\      |
|     /%%%\%%%/%%%\   /%%%\%%%/%%%\     |
|    /%%%%%\%/%%%%%\ /%%%%%\%/%%%%%\    |
|   o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o   |
|   |\%%%%%/ \%%%%%/%\%%%%%/ \%%%%%/|   |
|   | \%%%/   \%%%/%%%\%%%/   \%%%/ |   |
|   |  \%/     \%/%%%%%\%/     \%/  |   |
|   |   o       o%%%%%%%o       o   |   |
|   |   |\     /%\%%%%%/%\     /|   |   |
|   |   | \   /%%%\%%%/%%%\   / |   |   |
|   | u |  \ /%%%%%\%/%%%%%\ /  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 1.2.  Ef = ((u + du)(v + dv))

Figure 1.3 expands \(\mathrm{D}f = f + \mathrm{E}f\) over \([u, v]\!\) to produce:

\(\texttt{uv~du~dv ~+~ u(v)~du(dv) ~+~ (u)v~(du)dv ~+~ (u)(v)~((du)(dv))}\) 
o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              / \     / \              |
|             /   \   /   \             |
|            /     \ /     \            |
|           o       o       o           |
|          / \     /%\     / \          |
|         /   \   /%%%\   /   \         |
|        /     \ /%%%%%\ /     \        |
|       o       o%%%%%%%o       o       |
|      / \     / \%%%%%/ \     / \      |
|     /   \   /   \%%%/   \   /   \     |
|    /     \ /     \%/     \ /     \    |
|   o       o       o       o       o   |
|   |\     /%\     /%\     /%\     /|   |
|   | \   /%%%\   /%%%\   /%%%\   / |   |
|   |  \ /%%%%%\ /%%%%%\ /%%%%%\ /  |   |
|   |   o%%%%%%%o%%%%%%%o%%%%%%%o   |   |
|   |   |\%%%%%/%\%%%%%/%\%%%%%/|   |   |
|   |   | \%%%/%%%\%%%/%%%\%%%/ |   |   |
|   | u |  \%/%%%%%\%/%%%%%\%/  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 1.3.  Df = f + Ef

I'll break this here in case anyone wants to try and do the work for \(g\!\) on their own.

Computation Summary \[g(u, v) = \texttt{((u,~v))}\]

The venn diagram in Figure 2.1 shows how the proposition \(g = \texttt{((u,~v))}\) can be expanded over the universe of discourse \([u, v]\!\) to produce a logically equivalent exclusive disjunction, namely, \(\texttt{uv ~+~ (u)(v)}.\) 

o---------------------------------------o
|                                       |
|                   o                   |
|                  /%\                  |
|                 /%%%\                 |
|                /%%%%%\                |
|               o%%%%%%%o               |
|              /%\%%%%%/%\              |
|             /%%%\%%%/%%%\             |
|            /%%%%%\%/%%%%%\            |
|           o%%%%%%%o%%%%%%%o           |
|          / \%%%%%/%\%%%%%/ \          |
|         /   \%%%/%%%\%%%/   \         |
|        /     \%/%%%%%\%/     \        |
|       o       o%%%%%%%o       o       |
|      / \     / \%%%%%/ \     / \      |
|     /   \   /   \%%%/   \   /   \     |
|    /     \ /     \%/     \ /     \    |
|   o       o       o       o       o   |
|   |\     / \     /%\     / \     /|   |
|   | \   /   \   /%%%\   /   \   / |   |
|   |  \ /     \ /%%%%%\ /     \ /  |   |
|   |   o       o%%%%%%%o       o   |   |
|   |   |\     /%\%%%%%/%\     /|   |   |
|   |   | \   /%%%\%%%/%%%\   / |   |   |
|   | u |  \ /%%%%%\%/%%%%%\ /  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/%\%%%%%/    |       |
|       |     \%%%/%%%\%%%/     |       |
|       | du   \%/%%%%%\%/   dv |       |
|       o-------o%%%%%%%o-------o       |
|                \%%%%%/                |
|                 \%%%/                 |
|                  \%/                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 2.1.  g = ((u, v))

Figure 2.2 expands \(\mathrm{E}g = \texttt{((u + du,~v + dv))}\) over \([u, v]\!\) to give:

\(\texttt{uv~((du,~dv)) ~+~ u(v)~(du,~dv) ~+~ (u)v~(du,~dv) ~+~ (u)(v)~((du,~dv))}\) 
o---------------------------------------o
|                                       |
|                   o                   |
|                  /%\                  |
|                 /%%%\                 |
|                /%%%%%\                |
|               o%%%%%%%o               |
|              / \%%%%%/ \              |
|             /   \%%%/   \             |
|            /     \%/     \            |
|           o       o       o           |
|          /%\     /%\     /%\          |
|         /%%%\   /%%%\   /%%%\         |
|        /%%%%%\ /%%%%%\ /%%%%%\        |
|       o%%%%%%%o%%%%%%%o%%%%%%%o       |
|      / \%%%%%/ \%%%%%/ \%%%%%/ \      |
|     /   \%%%/   \%%%/   \%%%/   \     |
|    /     \%/     \%/     \%/     \    |
|   o       o       o       o       o   |
|   |\     /%\     /%\     /%\     /|   |
|   | \   /%%%\   /%%%\   /%%%\   / |   |
|   |  \ /%%%%%\ /%%%%%\ /%%%%%\ /  |   |
|   |   o%%%%%%%o%%%%%%%o%%%%%%%o   |   |
|   |   |\%%%%%/ \%%%%%/ \%%%%%/|   |   |
|   |   | \%%%/   \%%%/   \%%%/ |   |   |
|   | u |  \%/     \%/     \%/  | v |   |
|   o---+---o       o       o---+---o   |
|       |    \     /%\     /    |       |
|       |     \   /%%%\   /     |       |
|       | du   \ /%%%%%\ /   dv |       |
|       o-------o%%%%%%%o-------o       |
|                \%%%%%/                |
|                 \%%%/                 |
|                  \%/                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 2.2.  Eg = ((u + du, v + dv))

Figure 2.3 expands \(\mathrm{D}g = g + \mathrm{E}g\) over \([u, v]\!\) to yield the form:

\(\texttt{uv~(du,~dv) ~+~ u(v)~(du,~dv) ~+~ (u)v~(du,~dv) ~+~ (u)(v)~(du,~dv)}\!\) 
o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              /%\     /%\              |
|             /%%%\   /%%%\             |
|            /%%%%%\ /%%%%%\            |
|           o%%%%%%%o%%%%%%%o           |
|          /%\%%%%%/ \%%%%%/%\          |
|         /%%%\%%%/   \%%%/%%%\         |
|        /%%%%%\%/     \%/%%%%%\        |
|       o%%%%%%%o       o%%%%%%%o       |
|      / \%%%%%/ \     / \%%%%%/ \      |
|     /   \%%%/   \   /   \%%%/   \     |
|    /     \%/     \ /     \%/     \    |
|   o       o       o       o       o   |
|   |\     /%\     / \     /%\     /|   |
|   | \   /%%%\   /   \   /%%%\   / |   |
|   |  \ /%%%%%\ /     \ /%%%%%\ /  |   |
|   |   o%%%%%%%o       o%%%%%%%o   |   |
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
|   | u |  \%/%%%%%\ /%%%%%\%/  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 2.3.  Dg = g + Eg

Differential : Locally Linear Approximation

 

'Tis a derivative from me to mine,
And only that I stand for.

  — Winter's Tale, 3.2.43–44

We've talked about differentials long enough that I think it's way past time we met with some.

When the term is being used with its more exact sense, a differential is a locally linear approximation to a function, in the context of this logical discussion, then, a locally linear approximation to a proposition.

Recall the form of the current example:

\(\begin{array}{lllll} F & = & (f, g) & = & ( ~\texttt{((u)(v))}~ , ~\texttt{((u,~v))}~ ). \end{array}\)

To speed things along, I will skip a mass of motivating discussion and just exhibit the simplest form of a differential \(\mathrm{d}F\!\) for the current example of a logical transformation \(F,\!\) after which the majority of the easiest questions will have been answered in visually intuitive terms.

For \(F = (f, g)\!\) we have \(\mathrm{d}F = (\mathrm{d}f, \mathrm{d}g),\) and so we can proceed componentwise, patching the pieces back together at the end.

We have prepared the ground already by computing these terms:

\(\begin{array}{lll} \mathrm{E}f & = & \texttt{(( u + du )( v + dv ))} \\ \\ \mathrm{E}g & = & \texttt{(( u + du ,~ v + dv ))} \\ \\ \mathrm{D}f & = & \texttt{((u)(v)) ~+~ (( u + du )( v + dv ))} \\ \\ \mathrm{D}g & = & \texttt{((u,~v)) ~+~ (( u + du ,~ v + dv ))} \end{array}\!\)

As a matter of fact, computing the symmetric differences \(\mathrm{D}f = f + \mathrm{E}f\) and \(\mathrm{D}g = g + \mathrm{E}g\) has already taken care of the localizing part of the task by subtracting out the forms of \(f\!\) and \(g\!\) from the forms of \(\mathrm{E}f\) and \(\mathrm{E}g,\) respectively. Thus all we have left to do is to decide what linear propositions best approximate the difference maps \(\mathrm{D}f\) and \(\mathrm{D}g,\) respectively.

This raises the question: What is a linear proposition?

The answer that makes the most sense in this context is this: A proposition is just a boolean-valued function, so a linear proposition is a linear function into the boolean space \(\mathbb{B}.\)

In particular, the linear functions that we want will be linear functions in the differential variables \(du\!\) and \(dv.\!\)

As it turns out, there are just four linear propositions in the associated differential universe \(\mathrm{d}U^\bullet = [du, dv],\) and these are the propositions that are commonly denoted\[\texttt{0}, \texttt{du}, \texttt{dv}, \texttt{du + dv},\] in other words, \(\texttt{()}, \texttt{du}, \texttt{dv}, \texttt{(du, dv)}.\)

Notions of Approximation

 

for equalities are so weighed
that curiosity in neither can
make choice of either's moiety.

  — King Lear, Sc.1.5–7 (Quarto)
 

for qualities are so weighed
that curiosity in neither can
make choice of either's moiety.

  — King Lear, 1.1.5–6 (Folio)

Justifying a notion of approximation is a little more involved in general, and especially in these discrete logical spaces, than it would be expedient for people in a hurry to tangle with right now. I will just say that there are naive or obvious notions and there are sophisticated or subtle notions that we might choose among. The later would engage us in trying to construct proper logical analogues of Lie derivatives, and so let's save that for when we have become subtle or sophisticated or both. Against or toward that day, as you wish, let's begin with an option in plain view.

Figure 1.4 illustrates one way of ranging over the cells of the underlying universe \(U^\bullet = [u, v]\!\) and selecting at each cell the linear proposition in \(\mathrm{d}U^\bullet = [du, dv]\) that best approximates the patch of the difference map \(\mathrm{D}f\) that is located there, yielding the following formula for the differential \(\mathrm{d}f.\)

\(\mathrm{d}f ~=~ \texttt{uv} \cdot \texttt{0} ~+~ \texttt{u(v)} \cdot \texttt{du} ~+~ \texttt{(u)v} \cdot \texttt{dv} ~+~ \texttt{(u)(v)} \cdot \texttt{(du, dv)}\) 
o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              / \     / \              |
|             /   \   /   \             |
|            /     \ /     \            |
|           o       o       o           |
|          / \     / \     / \          |
|         /   \   /   \   /   \         |
|        /     \ /     \ /     \        |
|       o       o       o       o       |
|      / \     /%\     /%\     / \      |
|     /   \   /%%%\   /%%%\   /   \     |
|    /     \ /%%%%%\ /%%%%%\ /     \    |
|   o       o%%%%%%%o%%%%%%%o       o   |
|   |\     /%\%%%%%/ \%%%%%/%\     /|   |
|   | \   /%%%\%%%/   \%%%/%%%\   / |   |
|   |  \ /%%%%%\%/     \%/%%%%%\ /  |   |
|   |   o%%%%%%%o       o%%%%%%%o   |   |
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
|   | u |  \%/%%%%%\ /%%%%%\%/  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 1.4.  df = linear approx to Df

Figure 2.4 illustrates one way of ranging over the cells of the underlying universe \(U^\bullet = [u, v]\!\) and selecting at each cell the linear proposition in \(\mathrm{d}U^\bullet = [du, dv]\) that best approximates the patch of the difference map \(\mathrm{D}g\) that is located there, yielding the following formula for the differential \(\mathrm{d}g.\!\)

\(\mathrm{d}g ~=~ \texttt{uv} \cdot \texttt{(du, dv)} ~+~ \texttt{u(v)} \cdot \texttt{(du, dv)} ~+~ \texttt{(u)v} \cdot \texttt{(du, dv)} ~+~ \texttt{(u)(v)} \cdot \texttt{(du, dv)}\) 
o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              /%\     /%\              |
|             /%%%\   /%%%\             |
|            /%%%%%\ /%%%%%\            |
|           o%%%%%%%o%%%%%%%o           |
|          /%\%%%%%/ \%%%%%/%\          |
|         /%%%\%%%/   \%%%/%%%\         |
|        /%%%%%\%/     \%/%%%%%\        |
|       o%%%%%%%o       o%%%%%%%o       |
|      / \%%%%%/ \     / \%%%%%/ \      |
|     /   \%%%/   \   /   \%%%/   \     |
|    /     \%/     \ /     \%/     \    |
|   o       o       o       o       o   |
|   |\     /%\     / \     /%\     /|   |
|   | \   /%%%\   /   \   /%%%\   / |   |
|   |  \ /%%%%%\ /     \ /%%%%%\ /  |   |
|   |   o%%%%%%%o       o%%%%%%%o   |   |
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
|   | u |  \%/%%%%%\ /%%%%%\%/  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 2.4.  dg = linear approx to Dg

Well, \(g,\!\) that was easy, seeing as how \(\mathrm{D}g\) is already linear at each locus, \(\mathrm{d}g = \mathrm{D}g.\)

Analytic Series

We have been conducting the differential analysis of the logical transformation \(F : [u, v] \mapsto [u, v]\) defined as \(F : (u, v) \mapsto ( ~\texttt{((u)(v))}~, ~\texttt{((u, v))}~ ),\) and this means starting with the extended transformation \(\mathrm{E}F : [u, v, du, dv] \to [u, v, du, dv]\) and breaking it into an analytic series, \(\mathrm{E}F = F + \mathrm{d}F + \mathrm{d}^2 F + \ldots,\) and so on until there is nothing left to analyze any further.

As a general rule, one proceeds by way of the following stages:

\(\begin{array}{lccccc} 1. & \mathrm{E}F & = & \mathrm{d}^0 F & + & \mathrm{r}^0 F \\ 2. & \mathrm{r}^0 F & = & \mathrm{d}^1 F & + & \mathrm{r}^1 F \\ 3. & \mathrm{r}^1 F & = & \mathrm{d}^2 F & + & \mathrm{r}^2 F \\ 4. & \ldots \end{array}\)

In our analysis of the transformation \(F,\!\) we carried out Step 1 in the more familiar form \(\mathrm{E}F = F + \mathrm{D}F,\) and we have just reached Step 2 in the form \(\mathrm{D}F = \mathrm{d}F + \mathrm{r}F,\) where \(\mathrm{r}F\) is the residual term that remains for us to examine next.

NB. I'm am trying to give quick overview here, and this forces me to omit many picky details. The picky reader may wish to consult the more detailed presentation of this material at the following locations:

Differential Logic and Dynamic Systems
The Secant Operator
Higher Dimensional Targets

Let's push on with the analysis of the transformation:

\(\begin{matrix} F & : & (u, v) & \mapsto & (f(u, v),~g(u, v)) & = & (~\texttt{((u)(v))}~,~\texttt{((u,~v))}~).\end{matrix}\)

For ease of comparison and computation, I will collect the Figures that we need for the remainder of the work together on one page.

Computation Summary \[f(u, v) = \texttt{((u)(v))}\]

Figure 1.1 shows the expansion of \(f = \texttt{((u)(v))}\) over \([u, v]\!\) to produce the expression:

\(\texttt{uv} ~+~ \texttt{u(v)} ~+~ \texttt{(u)v}\)

Figure 1.2 shows the expansion of \(\mathrm{E}f = \texttt{((u + du)(v + dv))}\) over \([u, v]\!\) to produce the expression:

\(\texttt{uv} \cdot \texttt{(du~dv)} + \texttt{u(v)} \cdot \texttt{(du (dv))} + \texttt{(u)v} \cdot \texttt{((du) dv)} + \texttt{(u)(v)} \cdot \texttt{((du)(dv))}\)

\(\mathrm{E}f\) tells you what you would have to do, from where you are in the universe \([u, v],\!\) if you want to end up in a place where \(f\!\) is true. In this case, where the prevailing proposition \(f\!\) is \(\texttt{((u)(v))},\) the indication \(\texttt{uv} \cdot \texttt{(du~dv)}\) of \(\mathrm{E}f\) tells you this: If \(u\!\) and \(v\!\) are both true where you are, then just don't change both \(u\!\) and \(v\!\) at once, and you will end up in a place where \(\texttt{((u)(v))}\) is true.

Figure 1.3 shows the expansion of \(\mathrm{D}f\) over \([u, v]\!\) to produce the expression:

\(\texttt{uv} \cdot \texttt{du~dv} ~+~ \texttt{u(v)} \cdot \texttt{du(dv)} ~+~ \texttt{(u)v} \cdot \texttt{(du)dv} ~+~ \texttt{(u)(v)} \cdot \texttt{((du)(dv))}\)

\(\mathrm{D}f\) tells you what you would have to do, from where you are in the universe \([u, v],\!\) if you want to bring about a change in the value of \(f,\!\) that is, if you want to get to a place where the value of \(f\!\) is different from what it is where you are. In the present case, where the reigning proposition \(f\!\) is \(\texttt{((u)(v))},\) the term \(\texttt{uv} \cdot \texttt{du~dv}\) of \(\mathrm{D}f\) tells you this: If \(u\!\) and \(v\!\) are both true where you are, then you would have to change both \(u\!\) and \(v\!\) in order to reach a place where the value of \(f\!\) is different from what it is where you are.

Figure 1.4 approximates \(\mathrm{D}f\) by the linear form \(\mathrm{d}f\) that expands over \([u, v]\!\) as follows:

\(\begin{matrix} \mathrm{d}f & = & \texttt{uv} \cdot \texttt{0} & + & \texttt{u(v)} \cdot \texttt{du} & + & \texttt{(u)v} \cdot \texttt{dv} & + & \texttt{(u)(v)} \cdot \texttt{(du, dv)} \\ \\ & = & & & \texttt{u(v)} \cdot \texttt{du} & + & \texttt{(u)v} \cdot \texttt{dv} & + & \texttt{(u)(v)} \cdot \texttt{(du, dv)} \end{matrix}\)

Figure 1.5 shows what remains of the difference map \(\mathrm{D}f\) when the first order linear contribution \(\mathrm{d}f\) is removed, namely:

\(\begin{matrix} \mathrm{r}f & = & \texttt{uv} \cdot \texttt{du~dv} & + & \texttt{u(v)} \cdot \texttt{du~dv} & + & \texttt{(u)v} \cdot \texttt{du~dv} & + & \texttt{(u)(v)} \cdot \texttt{du~dv} \\ \\ & = & \texttt{du~dv} \end{matrix}\) 

o---------------------------------------o
|                                       |
|                   o                   |
|                  /%\                  |
|                 /%%%\                 |
|                /%%%%%\                |
|               o%%%%%%%o               |
|              /%\%%%%%/%\              |
|             /%%%\%%%/%%%\             |
|            /%%%%%\%/%%%%%\            |
|           o%%%%%%%o%%%%%%%o           |
|          /%\%%%%%/%\%%%%%/%\          |
|         /%%%\%%%/%%%\%%%/%%%\         |
|        /%%%%%\%/%%%%%\%/%%%%%\        |
|       o%%%%%%%o%%%%%%%o%%%%%%%o       |
|      /%\%%%%%/%\%%%%%/%\%%%%%/%\      |
|     /%%%\%%%/%%%\%%%/%%%\%%%/%%%\     |
|    /%%%%%\%/%%%%%\%/%%%%%\%/%%%%%\    |
|   o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o   |
|   |\%%%%%/%\%%%%%/ \%%%%%/%\%%%%%/|   |
|   | \%%%/%%%\%%%/   \%%%/%%%\%%%/ |   |
|   |  \%/%%%%%\%/     \%/%%%%%\%/  |   |
|   |   o%%%%%%%o       o%%%%%%%o   |   |
|   |   |\%%%%%/ \     / \%%%%%/|   |   |
|   |   | \%%%/   \   /   \%%%/ |   |   |
|   | u |  \%/     \ /     \%/  | v |   |
|   o---+---o       o       o---+---o   |
|       |    \     / \     /    |       |
|       |     \   /   \   /     |       |
|       | du   \ /     \ /   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 1.1.  f = ((u)(v))



o---------------------------------------o
|                                       |
|                   o                   |
|                  /%\                  |
|                 /%%%\                 |
|                /%%%%%\                |
|               o%%%%%%%o               |
|              /%\%%%%%/%\              |
|             /%%%\%%%/%%%\             |
|            /%%%%%\%/%%%%%\            |
|           o%%%%%%%o%%%%%%%o           |
|          /%\%%%%%/ \%%%%%/%\          |
|         /%%%\%%%/   \%%%/%%%\         |
|        /%%%%%\%/     \%/%%%%%\        |
|       o%%%%%%%o       o%%%%%%%o       |
|      /%\%%%%%/%\     /%\%%%%%/%\      |
|     /%%%\%%%/%%%\   /%%%\%%%/%%%\     |
|    /%%%%%\%/%%%%%\ /%%%%%\%/%%%%%\    |
|   o%%%%%%%o%%%%%%%o%%%%%%%o%%%%%%%o   |
|   |\%%%%%/ \%%%%%/%\%%%%%/ \%%%%%/|   |
|   | \%%%/   \%%%/%%%\%%%/   \%%%/ |   |
|   |  \%/     \%/%%%%%\%/     \%/  |   |
|   |   o       o%%%%%%%o       o   |   |
|   |   |\     /%\%%%%%/%\     /|   |   |
|   |   | \   /%%%\%%%/%%%\   / |   |   |
|   | u |  \ /%%%%%\%/%%%%%\ /  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 1.2.  Ef = ((u + du)(v + dv))



o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              / \     / \              |
|             /   \   /   \             |
|            /     \ /     \            |
|           o       o       o           |
|          / \     /%\     / \          |
|         /   \   /%%%\   /   \         |
|        /     \ /%%%%%\ /     \        |
|       o       o%%%%%%%o       o       |
|      / \     / \%%%%%/ \     / \      |
|     /   \   /   \%%%/   \   /   \     |
|    /     \ /     \%/     \ /     \    |
|   o       o       o       o       o   |
|   |\     /%\     /%\     /%\     /|   |
|   | \   /%%%\   /%%%\   /%%%\   / |   |
|   |  \ /%%%%%\ /%%%%%\ /%%%%%\ /  |   |
|   |   o%%%%%%%o%%%%%%%o%%%%%%%o   |   |
|   |   |\%%%%%/%\%%%%%/%\%%%%%/|   |   |
|   |   | \%%%/%%%\%%%/%%%\%%%/ |   |   |
|   | u |  \%/%%%%%\%/%%%%%\%/  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 1.3.  Difference Map Df = f + Ef



o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              / \     / \              |
|             /   \   /   \             |
|            /     \ /     \            |
|           o       o       o           |
|          / \     / \     / \          |
|         /   \   /   \   /   \         |
|        /     \ /     \ /     \        |
|       o       o       o       o       |
|      / \     /%\     /%\     / \      |
|     /   \   /%%%\   /%%%\   /   \     |
|    /     \ /%%%%%\ /%%%%%\ /     \    |
|   o       o%%%%%%%o%%%%%%%o       o   |
|   |\     /%\%%%%%/ \%%%%%/%\     /|   |
|   | \   /%%%\%%%/   \%%%/%%%\   / |   |
|   |  \ /%%%%%\%/     \%/%%%%%\ /  |   |
|   |   o%%%%%%%o       o%%%%%%%o   |   |
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
|   | u |  \%/%%%%%\ /%%%%%\%/  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 1.4.  Linear Proxy df for Df



o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              / \     / \              |
|             /   \   /   \             |
|            /     \ /     \            |
|           o       o       o           |
|          / \     /%\     / \          |
|         /   \   /%%%\   /   \         |
|        /     \ /%%%%%\ /     \        |
|       o       o%%%%%%%o       o       |
|      / \     /%\%%%%%/%\     / \      |
|     /   \   /%%%\%%%/%%%\   /   \     |
|    /     \ /%%%%%\%/%%%%%\ /     \    |
|   o       o%%%%%%%o%%%%%%%o       o   |
|   |\     / \%%%%%/%\%%%%%/ \     /|   |
|   | \   /   \%%%/%%%\%%%/   \   / |   |
|   |  \ /     \%/%%%%%\%/     \ /  |   |
|   |   o       o%%%%%%%o       o   |   |
|   |   |\     / \%%%%%/ \     /|   |   |
|   |   | \   /   \%%%/   \   / |   |   |
|   | u |  \ /     \%/     \ /  | v |   |
|   o---+---o       o       o---+---o   |
|       |    \     / \     /    |       |
|       |     \   /   \   /     |       |
|       | du   \ /     \ /   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 1.5.  Remainder rf = Df + df

Computation Summary \[g(u, v) = \texttt{((u, v))}\]

Figure 2.1 shows the expansion of \(g = \texttt{((u, v))}\) over \([u, v]\!\) to produce the expression:

\(\texttt{uv} ~+~ \texttt{(u)(v)}\)

Figure 2.2 shows the expansion of \(\mathrm{E}g = \texttt{((u + du, v + dv))}\) over \([u, v]\!\) to produce the expression:

\(\texttt{uv} \cdot \texttt{((du, dv))} + \texttt{u(v)} \cdot \texttt{(du, dv)} + \texttt{(u)v} \cdot \texttt{(du, dv)} + \texttt{(u)(v)} \cdot \texttt{((du, dv))}\)

\(\mathrm{E}g\) tells you what you would have to do, from where you are in the universe \([u, v],\!\) if you want to end up in a place where \(g\!\) is true. In this case, where the prevailing proposition \(g\!\) is \(\texttt{((u, v))},\) the component \(\texttt{uv} \cdot \texttt{((du, dv))}\) of \(\mathrm{E}g\) tells you this: If \(u\!\) and \(v\!\) are both true where you are, then change either both or neither of \(u\!\) and \(v\!\) at the same time, and you will attain a place where \(\texttt{((du, dv))}\) is true.

Figure 2.3 shows the expansion of \(\mathrm{D}g\) over \([u, v]\!\) to produce the expression:

\(\texttt{uv} \cdot \texttt{(du, dv)} ~+~ \texttt{u(v)} \cdot \texttt{(du, dv)} ~+~ \texttt{(u)v} \cdot \texttt{(du, dv)} ~+~ \texttt{(u)(v)} \cdot \texttt{(du, dv)}\)

\(\mathrm{D}g\) tells you what you would have to do, from where you are in the universe \([u, v],\!\) if you want to bring about a change in the value of \(g,\!\) that is, if you want to get to a place where the value of \(g\!\) is different from what it is where you are. In the present case, where the ruling proposition \(g\!\) is \(\texttt{((u, v))},\) the term \(\texttt{uv} \cdot \texttt{(du, dv)}\) of \(\mathrm{D}g\) tells you this: If \(u\!\) and \(v\!\) are both true where you are, then you would have to change one or the other but not both \(u\!\) and \(v\!\) in order to reach a place where the value of \(g\!\) is different from what it is where you are.

Figure 2.4 approximates \(\mathrm{D}g\) by the linear form \(\mathrm{d}g\) that expands over \([u, v]\!\) as follows:

\(\begin{array}{lll} \mathrm{d}g & = & \texttt{uv}\!\cdot\!\texttt{(du, dv)} + \texttt{u(v)}\!\cdot\!\texttt{(du, dv)} + \texttt{(u)v}\!\cdot\!\texttt{(du, dv)} + \texttt{(u)(v)}\!\cdot\!\texttt{(du, dv)} \\ \\ & = & \texttt{(du, dv)} \end{array}\)

Figure 2.5 shows what remains of the difference map \(\mathrm{D}g\) when the first order linear contribution \(\mathrm{d}g\) is removed, namely:

\(\begin{matrix} \mathrm{r}g & = & \texttt{uv} \cdot \texttt{0} & + & \texttt{u(v)} \cdot \texttt{0} & + & \texttt{(u)v} \cdot \texttt{0} & + & \texttt{(u)(v)} \cdot \texttt{0} \\ \\ & = & \texttt{0} \end{matrix}\) 

o---------------------------------------o
|                                       |
|                   o                   |
|                  /%\                  |
|                 /%%%\                 |
|                /%%%%%\                |
|               o%%%%%%%o               |
|              /%\%%%%%/%\              |
|             /%%%\%%%/%%%\             |
|            /%%%%%\%/%%%%%\            |
|           o%%%%%%%o%%%%%%%o           |
|          / \%%%%%/%\%%%%%/ \          |
|         /   \%%%/%%%\%%%/   \         |
|        /     \%/%%%%%\%/     \        |
|       o       o%%%%%%%o       o       |
|      / \     / \%%%%%/ \     / \      |
|     /   \   /   \%%%/   \   /   \     |
|    /     \ /     \%/     \ /     \    |
|   o       o       o       o       o   |
|   |\     / \     /%\     / \     /|   |
|   | \   /   \   /%%%\   /   \   / |   |
|   |  \ /     \ /%%%%%\ /     \ /  |   |
|   |   o       o%%%%%%%o       o   |   |
|   |   |\     /%\%%%%%/%\     /|   |   |
|   |   | \   /%%%\%%%/%%%\   / |   |   |
|   | u |  \ /%%%%%\%/%%%%%\ /  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/%\%%%%%/    |       |
|       |     \%%%/%%%\%%%/     |       |
|       | du   \%/%%%%%\%/   dv |       |
|       o-------o%%%%%%%o-------o       |
|                \%%%%%/                |
|                 \%%%/                 |
|                  \%/                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 2.1.  g = ((u, v))



o---------------------------------------o
|                                       |
|                   o                   |
|                  /%\                  |
|                 /%%%\                 |
|                /%%%%%\                |
|               o%%%%%%%o               |
|              / \%%%%%/ \              |
|             /   \%%%/   \             |
|            /     \%/     \            |
|           o       o       o           |
|          /%\     /%\     /%\          |
|         /%%%\   /%%%\   /%%%\         |
|        /%%%%%\ /%%%%%\ /%%%%%\        |
|       o%%%%%%%o%%%%%%%o%%%%%%%o       |
|      / \%%%%%/ \%%%%%/ \%%%%%/ \      |
|     /   \%%%/   \%%%/   \%%%/   \     |
|    /     \%/     \%/     \%/     \    |
|   o       o       o       o       o   |
|   |\     /%\     /%\     /%\     /|   |
|   | \   /%%%\   /%%%\   /%%%\   / |   |
|   |  \ /%%%%%\ /%%%%%\ /%%%%%\ /  |   |
|   |   o%%%%%%%o%%%%%%%o%%%%%%%o   |   |
|   |   |\%%%%%/ \%%%%%/ \%%%%%/|   |   |
|   |   | \%%%/   \%%%/   \%%%/ |   |   |
|   | u |  \%/     \%/     \%/  | v |   |
|   o---+---o       o       o---+---o   |
|       |    \     /%\     /    |       |
|       |     \   /%%%\   /     |       |
|       | du   \ /%%%%%\ /   dv |       |
|       o-------o%%%%%%%o-------o       |
|                \%%%%%/                |
|                 \%%%/                 |
|                  \%/                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 2.2.  Eg = ((u + du, v + dv))



o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              /%\     /%\              |
|             /%%%\   /%%%\             |
|            /%%%%%\ /%%%%%\            |
|           o%%%%%%%o%%%%%%%o           |
|          /%\%%%%%/ \%%%%%/%\          |
|         /%%%\%%%/   \%%%/%%%\         |
|        /%%%%%\%/     \%/%%%%%\        |
|       o%%%%%%%o       o%%%%%%%o       |
|      / \%%%%%/ \     / \%%%%%/ \      |
|     /   \%%%/   \   /   \%%%/   \     |
|    /     \%/     \ /     \%/     \    |
|   o       o       o       o       o   |
|   |\     /%\     / \     /%\     /|   |
|   | \   /%%%\   /   \   /%%%\   / |   |
|   |  \ /%%%%%\ /     \ /%%%%%\ /  |   |
|   |   o%%%%%%%o       o%%%%%%%o   |   |
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
|   | u |  \%/%%%%%\ /%%%%%\%/  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 2.3.  Difference Map Dg = g + Eg



o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              /%\     /%\              |
|             /%%%\   /%%%\             |
|            /%%%%%\ /%%%%%\            |
|           o%%%%%%%o%%%%%%%o           |
|          /%\%%%%%/ \%%%%%/%\          |
|         /%%%\%%%/   \%%%/%%%\         |
|        /%%%%%\%/     \%/%%%%%\        |
|       o%%%%%%%o       o%%%%%%%o       |
|      / \%%%%%/ \     / \%%%%%/ \      |
|     /   \%%%/   \   /   \%%%/   \     |
|    /     \%/     \ /     \%/     \    |
|   o       o       o       o       o   |
|   |\     /%\     / \     /%\     /|   |
|   | \   /%%%\   /   \   /%%%\   / |   |
|   |  \ /%%%%%\ /     \ /%%%%%\ /  |   |
|   |   o%%%%%%%o       o%%%%%%%o   |   |
|   |   |\%%%%%/%\     /%\%%%%%/|   |   |
|   |   | \%%%/%%%\   /%%%\%%%/ |   |   |
|   | u |  \%/%%%%%\ /%%%%%\%/  | v |   |
|   o---+---o%%%%%%%o%%%%%%%o---+---o   |
|       |    \%%%%%/ \%%%%%/    |       |
|       |     \%%%/   \%%%/     |       |
|       | du   \%/     \%/   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 2.4.  Linear Proxy dg for Dg



o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              / \     / \              |
|             /   \   /   \             |
|            /     \ /     \            |
|           o       o       o           |
|          / \     / \     / \          |
|         /   \   /   \   /   \         |
|        /     \ /     \ /     \        |
|       o       o       o       o       |
|      / \     / \     / \     / \      |
|     /   \   /   \   /   \   /   \     |
|    /     \ /     \ /     \ /     \    |
|   o       o       o       o       o   |
|   |\     / \     / \     / \     /|   |
|   | \   /   \   /   \   /   \   / |   |
|   |  \ /     \ /     \ /     \ /  |   |
|   |   o       o       o       o   |   |
|   |   |\     / \     / \     /|   |   |
|   |   | \   /   \   /   \   / |   |   |
|   | u |  \ /     \ /     \ /  | v |   |
|   o---+---o       o       o---+---o   |
|       |    \     / \     /    |       |
|       |     \   /   \   /     |       |
|       | du   \ /     \ /   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o
Figure 2.5.  Remainder rg = Dg + dg



| Have I carved enough, my lord --
| Child, you are a bone.
|
| Leonard Cohen, "Teachers" (1967)

Visualization

In my work on Differential Logic and Dynamic Systems, I found it useful to develop several different ways of visualizing logical transformations, indeed, I devised four distinct styles of picture for the job. Thus far in our work on the mapping \(F : [u, v] \to [u, v],\!\) we've been making use of what I call the areal view of the extended universe of discourse, \([u, v, du, dv],\!\) but as the number of dimensions climbs beyond four, it's time to bid this genre adieu, and look for a style that can scale a little better. At any rate, before we proceed any further, let's first assemble the information that we have gathered about \(F\!\) from several different angles, and see if it can be fitted into a coherent picture of the transformation \(F : (u, v) \mapsto ( ~\texttt{((u)(v))}~, ~\texttt{((u, v))}~ ).\)

In our first crack at the transformation \(F,\!\) we simply plotted the state transitions and applied the utterly stock technique of calculating the finite differences.

\(\text{Orbit 1}\!\)

\(\begin{array}{c|cc|cc|} t & u & v & du & dv \'"`UNIQ-MathJax6-QINU`"' Another way to convey the same information is by means of the extended proposition'"`UNIQ-MathJax7-QINU`"' {| align="center" cellpadding="8" style="text-align:center" | \(\text{Orbit 2}\!\)

\(\begin{array}{c|cc|cc|cc|} t & u & v & du & dv & d^2 u & d^2 v \\[8pt] 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 & 1 & 1 & 1 \\ 2 & 1 & 0 & 0 & 0 & 0 & 0 \\ 3 & '' & '' & '' & '' & '' & '' \\ \end{array}\)

A more fine combing of the second Table brings to mind a rule that partly covers the remaining cases, that is, \(\texttt{du~=~v}, ~\texttt{dv~=~(u)}.\) This much information about Orbit 2 is also encapsulated by the extended proposition, \(\texttt{(uv)((du, v))(dv, u)},\) which says that \(u\!\) and \(v\!\) are not both true at the same time, while \(du\!\) is equal in value to \(v\!\) and \(dv\!\) is opposite in value to \(u.\!\)

Turing Machine Example

By way of providing a simple illustration of Cook's Theorem, namely, that “Propositional Satisfiability is NP-Complete”, I will describe one way to translate finite approximations of turing machines into propositional expressions, using the cactus language syntax for propositional calculus that I will describe in more detail as we proceed.

\(\mathrm{Stilt}(k) =\!\)
Space and time limited turing machine,
with \(k\!\) units of space and \(k\!\) units of time.
\(\mathrm{Stunt}(k) =\!\)
Space and time limited turing machine,
for computing the parity of a bit string, with number of tape cells of input equal to \(k.\!\)

I will follow the pattern of discussion in Herbert Wilf (1986), Algorithms and Complexity, pp. 188–201, but translate his logical formalism into cactus language, which is more efficient in regard to the number of propositional clauses that are required.

A turing machine for computing the parity of a bit string is described by means of the following Figure and Table. 


o-------------------------------------------------o
|                                                 |
|                     1/1/+1                      |
|                    -------->                    |
|                /\ /         \ /\                |
|       0/0/+1  ^  0           1  ^  0/0/+1       |
|                \/|\         /|\/                |
|                  | <-------- |                  |
|          #/#/-1  |  1/1/+1   |  #/#/-1          |
|                  |           |                  |
|                  v           v                  |
|                  #           *                  |
|                                                 |
o-------------------------------------------------o
Figure 21-a.  Parity Machine



Table 21-b.  Parity Machine
o-------o--------o-------------o---------o------------o
| State | Symbol | Next Symbol | Ratchet | Next State |
|   Q   |   S    |     S'      |   dR    |     Q'     |
o-------o--------o-------------o---------o------------o
|   0   |   0    |     0       |   +1    |     0      |
|   0   |   1    |     1       |   +1    |     1      |
|   0   |   #    |     #       |   -1    |     #      |
|   1   |   0    |     0       |   +1    |     1      |
|   1   |   1    |     1       |   +1    |     0      |
|   1   |   #    |     #       |   -1    |     *      |
o-------o--------o-------------o---------o------------o


The TM has a finite automaton (FA) as one component. Let us refer to this particular FA by the name of \(\mathrm{M}.\)

The tape head (that is, the read unit) will be called \(\mathrm{H}.\) The registers are also called tape cells or tape squares.

Finite Approximations

To see how each finite approximation to a given turing machine can be given a purely propositional description, one fixes the parameter \(k\!\) and limits the rest of the discussion to describing \(\mathrm{Stilt}(k),\!\) which is not really a full-fledged TM anymore but just a finite automaton in disguise.

In this example, for the sake of a minimal illustration, we choose \(k = 2,\!\) and discuss \(\mathrm{Stunt}(2).\) Since the zeroth tape cell and the last tape cell are both occupied by the character \(^{\backprime\backprime}\texttt{\#}^{\prime\prime}\) that is used for both the beginning of file \((\mathrm{bof})\) and the end of file \((\mathrm{eof})\) markers, this allows for only one digit of significant computation.

To translate \(\mathrm{Stunt}(2)\) into propositional form we use the following collection of basic propositions, boolean variables, or logical features, depending on what one prefers to call them:

The basic propositions for describing the present state function \(\mathrm{QF} : P \to Q\) are these:

\(\begin{matrix} \texttt{p0\_q\#}, & \texttt{p0\_q*}, & \texttt{p0\_q0}, & \texttt{p0\_q1}, \\[6pt] \texttt{p1\_q\#}, & \texttt{p1\_q*}, & \texttt{p1\_q0}, & \texttt{p1\_q1}, \\[6pt] \texttt{p2\_q\#}, & \texttt{p2\_q*}, & \texttt{p2\_q0}, & \texttt{p2\_q1}, \\[6pt] \texttt{p3\_q\#}, & \texttt{p3\_q*}, & \texttt{p3\_q0}, & \texttt{p3\_q1}. \end{matrix}\)

The proposition of the form \(\texttt{pi\_qj}\) says:

At the point-in-time \(p_i,\!\) the finite state machine \(\mathrm{M}\) is in the state \(q_j.\!\)

The basic propositions for describing the present register function \(\mathrm{RF} : P \to R\) are these:

\(\begin{matrix} \texttt{p0\_r0}, & \texttt{p0\_r1}, & \texttt{p0\_r2}, & \texttt{p0\_r3}, \\[6pt] \texttt{p1\_r0}, & \texttt{p1\_r1}, & \texttt{p1\_r2}, & \texttt{p1\_r3}, \\[6pt] \texttt{p2\_r0}, & \texttt{p2\_r1}, & \texttt{p2\_r2}, & \texttt{p2\_r3}, \\[6pt] \texttt{p3\_r0}, & \texttt{p3\_r1}, & \texttt{p3\_r2}, & \texttt{p3\_r3}. \end{matrix}\)

The proposition of the form \(\texttt{pi\_rj}\) says:

At the point-in-time \(p_i,\!\) the tape head \(\mathrm{H}\) is on the tape cell \(r_j.\!\)

The basic propositions for describing the present symbol function \(\mathrm{SF} : P \to (R \to S)\) are these:

\(\begin{matrix} \texttt{p0\_r0\_s\#}, & \texttt{p0\_r0\_s*}, & \texttt{p0\_r0\_s0}, & \texttt{p0\_r0\_s1}, \\[4pt] \texttt{p0\_r1\_s\#}, & \texttt{p0\_r1\_s*}, & \texttt{p0\_r1\_s0}, & \texttt{p0\_r1\_s1}, \\[4pt] \texttt{p0\_r2\_s\#}, & \texttt{p0\_r2\_s*}, & \texttt{p0\_r2\_s0}, & \texttt{p0\_r2\_s1}, \\[4pt] \texttt{p0\_r3\_s\#}, & \texttt{p0\_r3\_s*}, & \texttt{p0\_r3\_s0}, & \texttt{p0\_r3\_s1}, \\[12pt] \texttt{p1\_r0\_s\#}, & \texttt{p1\_r0\_s*}, & \texttt{p1\_r0\_s0}, & \texttt{p1\_r0\_s1}, \\[4pt] \texttt{p1\_r1\_s\#}, & \texttt{p1\_r1\_s*}, & \texttt{p1\_r1\_s0}, & \texttt{p1\_r1\_s1}, \\[4pt] \texttt{p1\_r2\_s\#}, & \texttt{p1\_r2\_s*}, & \texttt{p1\_r2\_s0}, & \texttt{p1\_r2\_s1}, \\[4pt] \texttt{p1\_r3\_s\#}, & \texttt{p1\_r3\_s*}, & \texttt{p1\_r3\_s0}, & \texttt{p1\_r3\_s1}, \\[12pt] \texttt{p2\_r0\_s\#}, & \texttt{p2\_r0\_s*}, & \texttt{p2\_r0\_s0}, & \texttt{p2\_r0\_s1}, \\[4pt] \texttt{p2\_r1\_s\#}, & \texttt{p2\_r1\_s*}, & \texttt{p2\_r1\_s0}, & \texttt{p2\_r1\_s1}, \\[4pt] \texttt{p2\_r2\_s\#}, & \texttt{p2\_r2\_s*}, & \texttt{p2\_r2\_s0}, & \texttt{p2\_r2\_s1}, \\[4pt] \texttt{p2\_r3\_s\#}, & \texttt{p2\_r3\_s*}, & \texttt{p2\_r3\_s0}, & \texttt{p2\_r3\_s1}, \\[12pt] \texttt{p3\_r0\_s\#}, & \texttt{p3\_r0\_s*}, & \texttt{p3\_r0\_s0}, & \texttt{p3\_r0\_s1}, \\[4pt] \texttt{p3\_r1\_s\#}, & \texttt{p3\_r1\_s*}, & \texttt{p3\_r1\_s0}, & \texttt{p3\_r1\_s1}, \\[4pt] \texttt{p3\_r2\_s\#}, & \texttt{p3\_r2\_s*}, & \texttt{p3\_r2\_s0}, & \texttt{p3\_r2\_s1}, \\[4pt] \texttt{p3\_r3\_s\#}, & \texttt{p3\_r3\_s*}, & \texttt{p3\_r3\_s0}, & \texttt{p3\_r3\_s1}. \end{matrix}\)

The proposition of the form \(\texttt{pi\_rj\_sk}\) says:

At the point-in-time \(p_i,\!\) the tape cell \(r_j\!\) bears the mark \(s_k.\!\)

Initial Conditions

Given but a single free square on the tape, there are just two different sets of initial conditions for \(\mathrm{Stunt}(2),\) the finite approximation to the parity turing machine that we are presently considering.

Initial Conditions for Tape Input "0"

The following conjunction of 5 basic propositions describes the initial conditions when \(\mathrm{Stunt}(2)\) is started with an input of "0" in its free square:

\(\begin{array}{l} \texttt{p0\_q0} \\ \\ \texttt{p0\_r1} \\ \\ \texttt{p0\_r0\_s\#} \\ \texttt{p0\_r1\_s0} \\ \texttt{p0\_r2\_s\#} \end{array}\)

This conjunction of basic propositions may be read as follows:

At time \(p_0,\!\) machine \(\mathrm{M}\) is in the state \(q_0,\!\)

At time \(p_0,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\)

At time \(p_0,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\)

At time \(p_0,\!\) cell \(r_1\!\) contains the symbol \(\texttt{0},\)

At time \(p_0,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#}.\)

Initial Conditions for Tape Input "1"

The following conjunction of 5 basic propositions describes the initial conditions when \(\mathrm{Stunt}(2)\) is started with an input of "1" in its free square:

\(\begin{array}{l} \texttt{p0\_q0} \\ \\ \texttt{p0\_r1} \\ \\ \texttt{p0\_r0\_s\#} \\ \texttt{p0\_r1\_s1} \\ \texttt{p0\_r2\_s\#} \end{array}\)

This conjunction of basic propositions may be read as follows:

At time \(p_0,\!\) machine \(\mathrm{M}\) is in the state \(q_0,\!\)

At time \(p_0,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\)

At time \(p_0,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\)

At time \(p_0,\!\) cell \(r_1\!\) contains the symbol \(\texttt{1},\)

At time \(p_0,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#}.\)

Propositional Program

A complete description of \(\mathrm{Stunt}(2)\) in propositional form is obtained by conjoining one of the above choices for initial conditions with all of the following sets of propositions, that serve in effect as a simple type of declarative program, telling us all that we need to know about the anatomy and behavior of the truncated TM in question.

Mediate Conditions

\(\begin{array}{l} \texttt{(~p0\_q\#~(~p1\_q\#~))} \\ \texttt{(~p0\_q*~(~p1\_q*~))} \\ \\ \texttt{(~p1\_q\#~(~p2\_q\#~))} \\ \texttt{(~p1\_q*~(~p2\_q*~))} \end{array}\)

Terminal Conditions

\(\begin{array}{l} \texttt{((~p2\_q\#~)(~p2\_q*~))} \end{array}\)

State Partition

\(\begin{array}{l} \texttt{((~p0\_q0~),(~p0\_q1~),(~p0\_q\#~),(~p0\_q*~))} \\ \texttt{((~p1\_q0~),(~p1\_q1~),(~p1\_q\#~),(~p1\_q*~))} \\ \texttt{((~p2\_q0~),(~p2\_q1~),(~p2\_q\#~),(~p2\_q*~))} \end{array}\)

Register Partition

\(\begin{array}{l} \texttt{((~p0\_r0~),(~p0\_r1~),(~p0\_r2~))} \\ \texttt{((~p1\_r0~),(~p1\_r1~),(~p1\_r2~))} \\ \texttt{((~p2\_r0~),(~p2\_r1~),(~p2\_r2~))} \end{array}\)

Symbol Partition

\(\begin{array}{l} \texttt{((~p0\_r0\_s0~),(~p0\_r0\_s1~),(~p0\_r0\_s\#~))} \\ \texttt{((~p0\_r1\_s0~),(~p0\_r1\_s1~),(~p0\_r1\_s\#~))} \\ \texttt{((~p0\_r2\_s0~),(~p0\_r2\_s1~),(~p0\_r2\_s\#~))} \\ \\ \texttt{((~p1\_r0\_s0~),(~p1\_r0\_s1~),(~p1\_r0\_s\#~))} \\ \texttt{((~p1\_r1\_s0~),(~p1\_r1\_s1~),(~p1\_r1\_s\#~))} \\ \texttt{((~p1\_r2\_s0~),(~p1\_r2\_s1~),(~p1\_r2\_s\#~))} \\ \\ \texttt{((~p2\_r0\_s0~),(~p2\_r0\_s1~),(~p2\_r0\_s\#~))} \\ \texttt{((~p2\_r1\_s0~),(~p2\_r1\_s1~),(~p2\_r1\_s\#~))} \\ \texttt{((~p2\_r2\_s0~),(~p2\_r2\_s1~),(~p2\_r2\_s\#~))} \end{array}\)

Interaction Conditions

\(\begin{array}{l} \texttt{((~p0\_r0~) ~p0\_r0\_s0~ (~p1\_r0\_s0~))} \\ \texttt{((~p0\_r0~) ~p0\_r0\_s1~ (~p1\_r0\_s1~))} \\ \texttt{((~p0\_r0~) ~p0\_r0\_s\#~ (~p1\_r0\_s\#~))} \\ \\ \texttt{((~p0\_r1~) ~p0\_r1\_s0~ (~p1\_r1\_s0~))} \\ \texttt{((~p0\_r1~) ~p0\_r1\_s1~ (~p1\_r1\_s1~))} \\ \texttt{((~p0\_r1~) ~p0\_r1\_s\#~ (~p1\_r1\_s\#~))} \\ \\ \texttt{((~p0\_r2~) ~p0\_r2\_s0~ (~p1\_r2\_s0~))} \\ \texttt{((~p0\_r2~) ~p0\_r2\_s1~ (~p1\_r2\_s1~))} \\ \texttt{((~p0\_r2~) ~p0\_r2\_s\#~ (~p1\_r2\_s\#~))} \\ \\ \texttt{((~p1\_r0~) ~p1\_r0\_s0~ (~p2\_r0\_s0~))} \\ \texttt{((~p1\_r0~) ~p1\_r0\_s1~ (~p2\_r0\_s1~))} \\ \texttt{((~p1\_r0~) ~p1\_r0\_s\#~ (~p2\_r0\_s\#~))} \\ \\ \texttt{((~p1\_r1~) ~p1\_r1\_s0~ (~p2\_r1\_s0~))} \\ \texttt{((~p1\_r1~) ~p1\_r1\_s1~ (~p2\_r1\_s1~))} \\ \texttt{((~p1\_r1~) ~p1\_r1\_s\#~ (~p2\_r1\_s\#~))} \\ \\ \texttt{((~p1\_r2~) ~p1\_r2\_s0~ (~p2\_r2\_s0~))} \\ \texttt{((~p1\_r2~) ~p1\_r2\_s1~ (~p2\_r2\_s1~))} \\ \texttt{((~p1\_r2~) ~p1\_r2\_s\#~ (~p2\_r2\_s\#~))} \end{array}\)

Transition Relations

\(\begin{array}{l} \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s0~~(~p1\_q0~~p1\_r2~~p1\_r1\_s0~))} \\ \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s1~~(~p1\_q1~~p1\_r2~~p1\_r1\_s1~))} \\ \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q\#~~p1\_r0~~p1\_r1\_s\#~))} \\ \texttt{(~p0\_q0~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q\#~~p1\_r1~~p1\_r2\_s\#~))} \\ \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s0~~(~p1\_q1~~p1\_r2~~p1\_r1\_s0~))} \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s1~~(~p1\_q0~~p1\_r2~~p1\_r1\_s1~))} \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q*~~p1\_r0~~p1\_r1\_s\#~))} \\ \texttt{(~p0\_q1~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q*~~p1\_r1~~p1\_r2\_s\#~))} \\ \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s0~~(~p2\_q0~~p2\_r2~~p2\_r1\_s0~))} \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s1~~(~p2\_q1~~p2\_r2~~p2\_r1\_s1~))} \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q\#~~p2\_r0~~p2\_r1\_s\#~))} \\ \texttt{(~p1\_q0~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q\#~~p2\_r1~~p2\_r2\_s\#~))} \\ \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s0~~(~p2\_q1~~p2\_r2~~p2\_r1\_s0~))} \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s1~~(~p2\_q0~~p2\_r2~~p2\_r1\_s1~))} \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q*~~p2\_r0~~p2\_r1\_s\#~))} \\ \texttt{(~p1\_q1~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q*~~p2\_r1~~p2\_r2\_s\#~))} \end{array}\)

Interpretation of the Propositional Program

Let us now run through the propositional specification of \(\mathrm{Stunt}(2),\) our truncated TM, and paraphrase what it says in ordinary language.

Mediate Conditions

\(\begin{array}{l} \texttt{(~p0\_q\#~(~p1\_q\#~))} \\ \texttt{(~p0\_q*~(~p1\_q*~))} \\ \\ \texttt{(~p1\_q\#~(~p2\_q\#~))} \\ \texttt{(~p1\_q*~(~p2\_q*~))} \end{array}\)

In the interpretation of the cactus language for propositional logic that we are using here, an expression of the form \(\texttt{(p(q))}\) expresses a conditional, an implication, or an if-then proposition, commonly read in one of the following ways:

\(\begin{array}{l} \mathrm{not}~ p ~\mathrm{without}~ q \\[4pt] p ~\mathrm{implies}~ q \\[4pt] \mathrm{if}~ p ~\mathrm{then}~ q \\[4pt] p \Rightarrow q \end{array}\)

A text string expression of the form \(\texttt{(p(q))}\) corresponds to a graph-theoretic data-structure of the following form: 


o---------------------------------------o
|                                       |
|                 p   q                 |
|                 o---o                 |
|                 |                     |
|                 @                     |
|                                       |
o---------------------------------------o
|               ( p ( q ))              |
o---------------------------------------o


Taken together, the Mediate Conditions state the following:

If \(\mathrm{M}\) at \(p_0\!\) is in state \(q_\#,\!\) then \(\mathrm{M}\) at \(p_1\!\) is in state \(q_\#,\!\) and

If \(\mathrm{M}\) at \(p_0\!\) is in state \(q_*,\!\) then \(\mathrm{M}\) at \(p_1\!\) is in state \(q_*,\!\) and

If \(\mathrm{M}\) at \(p_1\!\) is in state \(q_\#,\!\) then \(\mathrm{M}\) at \(p_2\!\) is in state \(q_\#,\!\) and

If \(\mathrm{M}\) at \(p_1\!\) is in state \(q_*,\!\) then \(\mathrm{M}\) at \(p_2\!\) is in state \(q_*.\!\)

Terminal Conditions

\(\begin{array}{l} \texttt{((~p2\_q\#~)(~p2\_q*~))} \end{array}\)

In cactus syntax, an expression of the form \(\texttt{((p)(q))}\) expresses the disjunction \(p ~\mathrm{or}~ q.\) The corresponding cactus graph, here just a tree, has the following shape: 


o---------------------------------------o
|                                       |
|                 p   q                 |
|                 o   o                 |
|                  \ /                  |
|                   o                   |
|                   |                   |
|                   @                   |
|                                       |
o---------------------------------------o
|               ((p) (q))               |
o---------------------------------------o


In effect, the Terminal Conditions state the following:

At time \(p_2\!\) machine \(\mathrm{M}\) is in state \(q_\#,\!\) or

At time \(p_2\!\) machine \(\mathrm{M}\) is in state \(q_*.\!\)

State Partition

\(\begin{array}{l} \texttt{((~p0\_q0~),(~p0\_q1~),(~p0\_q\#~),(~p0\_q*~))} \\ \texttt{((~p1\_q0~),(~p1\_q1~),(~p1\_q\#~),(~p1\_q*~))} \\ \texttt{((~p2\_q0~),(~p2\_q1~),(~p2\_q\#~),(~p2\_q*~))} \end{array}\)

In cactus syntax, an expression of the form \(\texttt{((} e_1 \texttt{),(} e_2 \texttt{),(} \ldots \texttt{),(} e_k \texttt{))}\!\) expresses a statement to the effect that exactly one of the expressions \(e_j\!\) is true, for \(j = 1 ~\mathit{to}~ k.\) Expressions of this form are called universal partition expressions, and the corresponding painted and rooted cactus (PARC) has the following shape: 


o---------------------------------------o
|                                       |
|         e_1   e_2   ...   e_k         |
|          o     o           o          |
|          |     |           |          |
|          o-----o--- ... ---o          |
|           \               /           |
|            \             /            |
|             \           /             |
|              \         /              |
|               \       /               |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   @                   |
|                                       |
o---------------------------------------o
|       ((e_1),(e_2),(...),(e_k))       |
o---------------------------------------o


The State Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction expressing the condition that \(\mathrm{M}\) has to be in one and only one of its states at each point in time under consideration. In short, we have the constraint:

At each of the points in time \(p_i,\!\) for \(i\!\) in the set \(\{ 0, 1, 2 \},\!\)

\(\mathrm{M}\) can be in exactly one state \(q_j,\!\) for \(j\!\) in the set \(\{ 0, 1, \#, * \}.\!\)

Register Partition

\(\begin{array}{l} \texttt{((~p0\_r0~),(~p0\_r1~),(~p0\_r2~))} \\ \texttt{((~p1\_r0~),(~p1\_r1~),(~p1\_r2~))} \\ \texttt{((~p2\_r0~),(~p2\_r1~),(~p2\_r2~))} \end{array}\)

The Register Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction saying that the read head \(\mathrm{H}\) must be reading one and only one of the registers or tape cells available to it at each of the points in time under consideration. In sum:

At each of the points in time \(p_i,\!\) for \(i = 0, 1, 2,\!\)

\(\mathrm{H}\) is reading exactly one cell \(r_j,\!\) for \(j = 0, 1, 2.\!\)

Symbol Partition

\(\begin{array}{l} \texttt{((~p0\_r0\_s0~),(~p0\_r0\_s1~),(~p0\_r0\_s\#~))} \\ \texttt{((~p0\_r1\_s0~),(~p0\_r1\_s1~),(~p0\_r1\_s\#~))} \\ \texttt{((~p0\_r2\_s0~),(~p0\_r2\_s1~),(~p0\_r2\_s\#~))} \\ \\ \texttt{((~p1\_r0\_s0~),(~p1\_r0\_s1~),(~p1\_r0\_s\#~))} \\ \texttt{((~p1\_r1\_s0~),(~p1\_r1\_s1~),(~p1\_r1\_s\#~))} \\ \texttt{((~p1\_r2\_s0~),(~p1\_r2\_s1~),(~p1\_r2\_s\#~))} \\ \\ \texttt{((~p2\_r0\_s0~),(~p2\_r0\_s1~),(~p2\_r0\_s\#~))} \\ \texttt{((~p2\_r1\_s0~),(~p2\_r1\_s1~),(~p2\_r1\_s\#~))} \\ \texttt{((~p2\_r2\_s0~),(~p2\_r2\_s1~),(~p2\_r2\_s\#~))} \end{array}\)

The Symbol Partition segment of the propositional program for \(\mathrm{Stunt}(2)\) consists of nine universal partition expressions, taken in conjunction stipulating that there has to be one and only one symbol in each of the registers at each point in time under consideration. In short, we have:

At each of the points in time \(p_i,\!\) for \(i\!\) in \(\{ 0, 1, 2 \},\!\)

in each of the tape registers \(r_j,\!\) for \(j\!\) in \(\{ 0, 1, 2 \},\!\)

there can be exactly one sign \(s_k,\!\) for \(k\!\) in \(\{ 0, 1, \# \}.\!\)

Interaction Conditions

\(\begin{array}{l} \texttt{((~p0\_r0~) ~p0\_r0\_s0~ (~p1\_r0\_s0~))} \\ \texttt{((~p0\_r0~) ~p0\_r0\_s1~ (~p1\_r0\_s1~))} \\ \texttt{((~p0\_r0~) ~p0\_r0\_s\#~ (~p1\_r0\_s\#~))} \\ \\ \texttt{((~p0\_r1~) ~p0\_r1\_s0~ (~p1\_r1\_s0~))} \\ \texttt{((~p0\_r1~) ~p0\_r1\_s1~ (~p1\_r1\_s1~))} \\ \texttt{((~p0\_r1~) ~p0\_r1\_s\#~ (~p1\_r1\_s\#~))} \\ \\ \texttt{((~p0\_r2~) ~p0\_r2\_s0~ (~p1\_r2\_s0~))} \\ \texttt{((~p0\_r2~) ~p0\_r2\_s1~ (~p1\_r2\_s1~))} \\ \texttt{((~p0\_r2~) ~p0\_r2\_s\#~ (~p1\_r2\_s\#~))} \\ \\ \texttt{((~p1\_r0~) ~p1\_r0\_s0~ (~p2\_r0\_s0~))} \\ \texttt{((~p1\_r0~) ~p1\_r0\_s1~ (~p2\_r0\_s1~))} \\ \texttt{((~p1\_r0~) ~p1\_r0\_s\#~ (~p2\_r0\_s\#~))} \\ \\ \texttt{((~p1\_r1~) ~p1\_r1\_s0~ (~p2\_r1\_s0~))} \\ \texttt{((~p1\_r1~) ~p1\_r1\_s1~ (~p2\_r1\_s1~))} \\ \texttt{((~p1\_r1~) ~p1\_r1\_s\#~ (~p2\_r1\_s\#~))} \\ \\ \texttt{((~p1\_r2~) ~p1\_r2\_s0~ (~p2\_r2\_s0~))} \\ \texttt{((~p1\_r2~) ~p1\_r2\_s1~ (~p2\_r2\_s1~))} \\ \texttt{((~p1\_r2~) ~p1\_r2\_s\#~ (~p2\_r2\_s\#~))} \end{array}\)

In briefest terms, the Interaction Conditions simply express the circumstance that the mark on a tape cell cannot change between two points in time unless the tape head is over the cell in question at the initial one of those points in time. All that we have to do is to see how they manage to say this.

Consider a cactus expression of the following form:

\(\begin{array}{l} \texttt{((}~ p_i\_r_j ~\texttt{)}~ p_i\_r_j\_s_k ~\texttt{(}~ p_{i+1}\_r_j\_s_k ~\texttt{))} \end{array}\)

This expression has the corresponding cactus graph: 

o---------------------------------------o
|                                       |
|         p<i>_r<j>   p<i+1>_r<j>_s<k>  |
|                 o   o                 |
|                  \ /                  |
|    p<i>_r<j>_s<k> o                   |
|                   |                   |
|                   @                   |
|                                       |
o---------------------------------------o

A propositional expression of this form can be read as follows:

\(\mathrm{If}\)
At the time \(p_i,\!\) the tape cell \(r_j\!\) bears the mark \(s_k,\!\)
\(\mathrm{But}\) it is not the case that:
At the time \(p_i,\!\) the tape head is on the tape cell \(r_j,\!\)
\(\mathrm{Then}\)
At the time \(p_{i+1},\!\) the tape cell \(r_j\!\) bears the mark \(s_k.\!\)

The eighteen clauses of the Interaction Conditions simply impose one such constraint on symbol changes for each combination of the times \(p_0, p_1,\!\) registers \(r_0, r_1, r_2,\!\) and symbols \(s_0, s_1, s_\#.\!\)

Transition Relations

\(\begin{array}{l} \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s0~~(~p1\_q0~~p1\_r2~~p1\_r1\_s0~))} \\ \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s1~~(~p1\_q1~~p1\_r2~~p1\_r1\_s1~))} \\ \texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q\#~~p1\_r0~~p1\_r1\_s\#~))} \\ \texttt{(~p0\_q0~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q\#~~p1\_r1~~p1\_r2\_s\#~))} \\ \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s0~~(~p1\_q1~~p1\_r2~~p1\_r1\_s0~))} \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s1~~(~p1\_q0~~p1\_r2~~p1\_r1\_s1~))} \\ \texttt{(~p0\_q1~~p0\_r1~~p0\_r1\_s\#~~(~p1\_q*~~p1\_r0~~p1\_r1\_s\#~))} \\ \texttt{(~p0\_q1~~p0\_r2~~p0\_r2\_s\#~~(~p1\_q*~~p1\_r1~~p1\_r2\_s\#~))} \\ \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s0~~(~p2\_q0~~p2\_r2~~p2\_r1\_s0~))} \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s1~~(~p2\_q1~~p2\_r2~~p2\_r1\_s1~))} \\ \texttt{(~p1\_q0~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q\#~~p2\_r0~~p2\_r1\_s\#~))} \\ \texttt{(~p1\_q0~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q\#~~p2\_r1~~p2\_r2\_s\#~))} \\ \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s0~~(~p2\_q1~~p2\_r2~~p2\_r1\_s0~))} \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s1~~(~p2\_q0~~p2\_r2~~p2\_r1\_s1~))} \\ \texttt{(~p1\_q1~~p1\_r1~~p1\_r1\_s\#~~(~p2\_q*~~p2\_r0~~p2\_r1\_s\#~))} \\ \texttt{(~p1\_q1~~p1\_r2~~p1\_r2\_s\#~~(~p2\_q*~~p2\_r1~~p2\_r2\_s\#~))} \end{array}\)

The Transition Relation segment of the propositional program for \(\mathrm{Stunt}(2)\) consists of sixteen implication statements with complex antecedents and consequents. Taken together, these give propositional expression to the TM Figure and Table that were given at the outset.

Just by way of a single example, consider the clause:

\(\texttt{(~p0\_q0~~p0\_r1~~p0\_r1\_s1~~(~p1\_q1~~p1\_r2~~p1\_r1\_s1~))}\)

This complex implication statement can be read to say:

\(\mathrm{If}\)
At the time \(p_0,\!\) the machine \(\mathrm{M}\) is in the state \(q_0,\!\) and
At the time \(p_0,\!\) the scanner \(\mathrm{H}\) is reading cell \(r_1,\!\) and
At the time \(p_0,\!\) the tape cell \(r_1\!\) contains a \(\texttt{1},\)
\(\mathrm{Then}\)
At the time \(p_1,\!\) the machine \(\mathrm{M}\) is in the state \(q_1,\!\) and
At the time \(p_1,\!\) the scanner \(\mathrm{H}\) is reading cell \(r_2,\!\) and
At the time \(p_1,\!\) the tape cell \(r_1\!\) contains a \(\texttt{1}.\)

Computation

The propositional program for \(\mathrm{Stunt}(2)\) uses the following set of \(9 + 12 + 36 = 57\!\) basic propositions or boolean variables:

\(\begin{matrix} \texttt{p0\_r0}, & \texttt{p0\_r1}, & \texttt{p0\_r2}, \\[6pt] \texttt{p1\_r0}, & \texttt{p1\_r1}, & \texttt{p1\_r2}, \\[6pt] \texttt{p2\_r0}, & \texttt{p2\_r1}, & \texttt{p2\_r2}. \end{matrix}\)

\(\begin{matrix} \texttt{p0\_q\#}, & \texttt{p0\_q*}, & \texttt{p0\_q0}, & \texttt{p0\_q1}, \\[6pt] \texttt{p1\_q\#}, & \texttt{p1\_q*}, & \texttt{p1\_q0}, & \texttt{p1\_q1}, \\[6pt] \texttt{p2\_q\#}, & \texttt{p2\_q*}, & \texttt{p2\_q0}, & \texttt{p2\_q1}. \end{matrix}\)

\(\begin{matrix} \texttt{p0\_r0\_s\#}, & \texttt{p0\_r0\_s*}, & \texttt{p0\_r0\_s0}, & \texttt{p0\_r0\_s1}, \\[4pt] \texttt{p0\_r1\_s\#}, & \texttt{p0\_r1\_s*}, & \texttt{p0\_r1\_s0}, & \texttt{p0\_r1\_s1}, \\[4pt] \texttt{p0\_r2\_s\#}, & \texttt{p0\_r2\_s*}, & \texttt{p0\_r2\_s0}, & \texttt{p0\_r2\_s1}, \\[12pt] \texttt{p1\_r0\_s\#}, & \texttt{p1\_r0\_s*}, & \texttt{p1\_r0\_s0}, & \texttt{p1\_r0\_s1}, \\[4pt] \texttt{p1\_r1\_s\#}, & \texttt{p1\_r1\_s*}, & \texttt{p1\_r1\_s0}, & \texttt{p1\_r1\_s1}, \\[4pt] \texttt{p1\_r2\_s\#}, & \texttt{p1\_r2\_s*}, & \texttt{p1\_r2\_s0}, & \texttt{p1\_r2\_s1}, \\[12pt] \texttt{p2\_r0\_s\#}, & \texttt{p2\_r0\_s*}, & \texttt{p2\_r0\_s0}, & \texttt{p2\_r0\_s1}, \\[4pt] \texttt{p2\_r1\_s\#}, & \texttt{p2\_r1\_s*}, & \texttt{p2\_r1\_s0}, & \texttt{p2\_r1\_s1}, \\[4pt] \texttt{p2\_r2\_s\#}, & \texttt{p2\_r2\_s*}, & \texttt{p2\_r2\_s0}, & \texttt{p2\_r2\_s1}. \end{matrix}\)

This means that the propositional program itself is nothing but a single proposition or boolean function of the form \(p : \mathbb{B}^{57} \to \mathbb{B}.\)

An assignment of boolean values to the above set of boolean variables is called an interpretation of the proposition \(p,\!\) and any interpretation of \(p\!\) that makes the proposition \(p : \mathbb{B}^{57} \to \mathbb{B}\) evaluate to \(1\!\) is referred to as a satisfying interpretation of the proposition \(p.\!\) Another way to specify interpretations, instead of giving them as bit vectors in \(\mathbb{B}^{57}\) and trying to remember some arbitrary ordering of variables, is to give them in the form of singular propositions, that is, a conjunction of the form \(e_1 \cdot \ldots \cdot e_{57}\) where each \(e_j\!\) is either \(v_j\!\) or \(\texttt{(} v_j \texttt{)},\) that is, either the assertion or the negation of the boolean variable \({v_j},\!\) as \(j\!\) runs from 1 to 57. Even more briefly, the same information can be communicated simply by giving the conjunction of the asserted variables, with the understanding that each of the others is negated.

A satisfying interpretation of the proposition \(p\!\) supplies us with all the information of a complete execution history for the corresponding program, and so all we have to do in order to get the output of the program \(p\!\) is to read off the proper part of the data from the expression of this interpretation.

Output

One component of the \(\begin{smallmatrix}\mathrm{Theme~One}\end{smallmatrix}\) program that I wrote some years ago finds all the satisfying interpretations of propositions expressed in cactus syntax. It's not a polynomial time algorithm, as you may guess, but it was just barely efficient enough to do this example in the 500 K of spare memory that I had on an old 286 PC in about 1989, so I will give you the actual outputs from those trials.

Output Conditions for Tape Input "0"

Let \(p_0\!\) be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "0" with the proposition that describes the truncated turing machine \(\mathrm{Stunt}(2).\) As it turns out, \(p_0\!\) has a single satisfying interpretation. This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display: 


o-------------------------------------------------o
|                                                 |
| p0_q0                                           |
|  p0_r1                                          |
|   p0_r0_s#                                      |
|    p0_r1_s0                                     |
|     p0_r2_s#                                    |
|      p1_q0                                      |
|       p1_r2                                     |
|        p1_r2_s#                                 |
|         p1_r0_s#                                |
|          p1_r1_s0                               |
|           p2_q#                                 |
|            p2_r1                                |
|             p2_r0_s#                            |
|              p2_r1_s0                           |
|               p2_r2_s#                          |
|                                                 |
o-------------------------------------------------o


The Output Conditions for Tape Input "0" can be read as follows:

At the time \(p_0,\!\) machine \(\mathrm{M}\) is in the state \(q_0,\!\) and

At the time \(p_0,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\) and

At the time \(p_0,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_0,\!\) cell \(r_1\!\) contains the symbol \(\texttt{0},\) and

At the time \(p_0,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_1,\!\) machine \(\mathrm{M}\) is in the state \(q_0,\!\) and

At the time \(p_1,\!\) scanner \(\mathrm{H}\) is reading cell \(r_2,\!\) and

At the time \(p_1,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_1,\!\) cell \(r_1\!\) contains the symbol \(\texttt{0},\) and

At the time \(p_1,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_2,\!\) machine \(\mathrm{M}\) is in the state \(q_\#,\!\) and

At the time \(p_2,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\) and

At the time \(p_2,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_2,\!\) cell \(r_1\!\) contains the symbol \(\texttt{0},\) and

At the time \(p_2,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#}.\)

The output of \(\mathrm{Stunt}(2)\) being the symbol that rests under the tape head \(\mathrm{H}\) if and when the machine \(\mathrm{M}\) reaches one of its resting states, we get the result that \(\mathrm{Parity}(0) = 0.\)

Output Conditions for Tape Input "1"

Let \(p_1\!\) be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "1" with the proposition that describes the truncated turing machine \(\mathrm{Stunt}(2).\) As it turns out, \(p_1\!\) has a single satisfying interpretation. This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display: 


o-------------------------------------------------o
|                                                 |
| p0_q0                                           |
|  p0_r1                                          |
|   p0_r0_s#                                      |
|    p0_r1_s1                                     |
|     p0_r2_s#                                    |
|      p1_q1                                      |
|       p1_r2                                     |
|        p1_r2_s#                                 |
|         p1_r0_s#                                |
|          p1_r1_s1                               |
|           p2_q*                                 |
|            p2_r1                                |
|             p2_r0_s#                            |
|              p2_r1_s1                           |
|               p2_r2_s#                          |
|                                                 |
o-------------------------------------------------o


The Output Conditions for Tape Input "1" can be read as follows:

At the time \(p_0,\!\) machine \(\mathrm{M}\) is in the state \(q_0,\!\) and

At the time \(p_0,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\) and

At the time \(p_0,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_0,\!\) cell \(r_1\!\) contains the symbol \(\texttt{1},\) and

At the time \(p_0,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_1,\!\) machine \(\mathrm{M}\) is in the state \(q_1,\!\) and

At the time \(p_1,\!\) scanner \(\mathrm{H}\) is reading cell \(r_2,\!\) and

At the time \(p_1,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_1,\!\) cell \(r_1\!\) contains the symbol \(\texttt{1},\) and

At the time \(p_1,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_2,\!\) machine \(\mathrm{M}\) is in the state \(q_*,\!\) and

At the time \(p_2,\!\) scanner \(\mathrm{H}\) is reading cell \(r_1,\!\) and

At the time \(p_2,\!\) cell \(r_0\!\) contains the symbol \(\texttt{\#},\) and

At the time \(p_2,\!\) cell \(r_1\!\) contains the symbol \(\texttt{1},\) and

At the time \(p_2,\!\) cell \(r_2\!\) contains the symbol \(\texttt{\#}.\)

The output of \(\mathrm{Stunt}(2)\) being the symbol that rests under the tape head \(\mathrm{H}\) when and if the machine \(\mathrm{M}\) reaches one of its resting states, we get the result that \(\mathrm{Parity}(1) = 1.\)

Work Area

DATA 20.  http://forum.wolframscience.com/showthread.php?postid=791#post791

Let's see how this information about the transformation F,
arrived at by eyeballing the raw data, comports with what
we derived through a more systematic symbolic computation.

The results of the various operator actions that we have just
computed are summarized in Tables 66-i and 66-ii from my paper,
and I have attached these as a text file below.

Table 66-i.  Computation Summary for f<u, v> = ((u)(v))
o--------------------------------------------------------------------------------o
|                                                                                |
| !e!f  =  uv.    1      + u(v).    1      + (u)v.    1      + (u)(v).    0      |
|                                                                                |
|   Ef  =  uv. (du  dv)  + u(v). (du (dv)) + (u)v.((du) dv)  + (u)(v).((du)(dv)) |
|                                                                                |
|   Df  =  uv.  du  dv   + u(v).  du (dv)  + (u)v. (du) dv   + (u)(v).((du)(dv)) |
|                                                                                |
|   df  =  uv.    0      + u(v).  du       + (u)v.      dv   + (u)(v). (du, dv)  |
|                                                                                |
|   rf  =  uv.  du  dv   + u(v).  du  dv   + (u)v.  du  dv   + (u)(v).  du  dv   |
|                                                                                |
o--------------------------------------------------------------------------------o

Table 66-ii.  Computation Summary for g<u, v> = ((u, v))
o--------------------------------------------------------------------------------o
|                                                                                |
| !e!g  =  uv.    1      + u(v).    0      + (u)v.    0      + (u)(v).    1      |
|                                                                                |
|   Eg  =  uv.((du, dv)) + u(v). (du, dv)  + (u)v. (du, dv)  + (u)(v).((du, dv)) |
|                                                                                |
|   Dg  =  uv. (du, dv)  + u(v). (du, dv)  + (u)v. (du, dv)  + (u)(v). (du, dv)  |
|                                                                                |
|   dg  =  uv. (du, dv)  + u(v). (du, dv)  + (u)v. (du, dv)  + (u)(v). (du, dv)  |
|                                                                                |
|   rg  =  uv.    0      + u(v).    0      + (u)v.    0      + (u)(v).    0      |
|                                                                                |
o--------------------------------------------------------------------------------o


o---------------------------------------o
|                                       |
|                   o                   |
|                  / \                  |
|                 /   \                 |
|                /     \                |
|               o       o               |
|              / \     / \              |
|             /   \   /   \             |
|            /     \ /     \            |
|           o       o       o           |
|          / \     / \     / \          |
|         /   \   /   \   /   \         |
|        /     \ /     \ /     \        |
|       o       o       o       o       |
|      / \     / \     / \     / \      |
|     /   \   /   \   /   \   /   \     |
|    /     \ /     \ /     \ /     \    |
|   o       o       o       o       o   |
|   |\     / \     / \     / \     /|   |
|   | \   /   \   /   \   /   \   / |   |
|   |  \ /     \ /     \ /     \ /  |   |
|   |   o       o       o       o   |   |
|   |   |\     / \     / \     /|   |   |
|   |   | \   /   \   /   \   / |   |   |
|   | u |  \ /     \ /     \ /  | v |   |
|   o---+---o       o       o---+---o   |
|       |    \     / \     /    |       |
|       |     \   /   \   /     |       |
|       | du   \ /     \ /   dv |       |
|       o-------o       o-------o       |
|                \     /                |
|                 \   /                 |
|                  \ /                  |
|                   o                   |
|                                       |
o---------------------------------------o

Discussion

PD = Philip Dutton

PD: I've been watching your posts.

PD: I am not an expert on logic infrastructures but I find the posts
    interesting (despite not understanding much of it).  I am like
    the diagrams.  I have recently been trying to understand CA's
    using a particular perspective:  sinks and sources.  I think
    that all CA's are simply combinations of sinks and sources.
    How they interact (or intrude into each other's domains)
    would most likely be a result of the rules (and initial
    configuration of on or off cells).

PD: Anyway, to be short, I "see" diamond shapes quite often in
    your diagrams.  Triangles (either up or down) or diamonds
    (combination of an up and down triangle) make me think
    soley of sinks and sources.  I think of the diamond to
    be a source which, during the course of progression,
    is expanding (because it is producing) and then starts
    to act as a sink  (because it consumes) -- and hence the
    diamond.  I can't stop thinking about sinks and sources in
    CA's and so I thought I would ask you if there is some way
    to tie the two worlds together (CA's of sinks and sources
    together with your differential constructs).

PD: Any thoughts?

Yes, I'm hoping that there's a lot of stuff analogous to
R-world dynamics to be discovered in this B-world variety,
indeed, that's kind of why I set out on this investigation --
oh, gee, has it been that long? -- I guess about 1989 or so,
when I started to see this "differential logic" angle on what
I had previously studied in systems theory as the "qualitative
approach to differential equations".  I think we used to use the
words "attractor" and "basin" more often than "sink", but a source
is still a source as time goes by, and I do remember using the word
"sink" a lot when I was a freshperson in physics, before I got logic.

I have spent the last 15 years doing a funny mix of practice in stats
and theory in math, but I did read early works by Von Neumann, Burks,
Ulam, and later stuff by Holland on CA's.  Still, it may be a while
before I have re-heated my concrete intuitions about them in the
NKS way of thinking.

There are some fractal-looking pictures that emerge when
I turn to "higher order propositional expressions" (HOPE's).
I have discussed this topic elswhere on the web and can look
it up now if your are interested, but I am trying to make my
e-positions somewhat clearer for the NKS forum than I have
tried to do before.

But do not hestitate to dialogue all this stuff on the boards,
as that's what always seems to work the best.  What I've found
works best for me, as I can hardly remember what I was writing
last month without Google, is to archive a copy at one of the
other Google-visible discussion lists that I'm on at present.

Document History

Ontology List : Feb–Mar 2004

  1. http://suo.ieee.org/ontology/msg05457.html
  2. http://suo.ieee.org/ontology/msg05458.html
  3. http://suo.ieee.org/ontology/msg05459.html
  4. http://suo.ieee.org/ontology/msg05460.html
  5. http://suo.ieee.org/ontology/msg05461.html
  6. http://suo.ieee.org/ontology/msg05462.html
  7. http://suo.ieee.org/ontology/msg05463.html
  8. http://suo.ieee.org/ontology/msg05464.html
  9. http://suo.ieee.org/ontology/msg05465.html
  10. http://suo.ieee.org/ontology/msg05466.html
  11. http://suo.ieee.org/ontology/msg05467.html
  12. http://suo.ieee.org/ontology/msg05469.html
  13. http://suo.ieee.org/ontology/msg05470.html
  14. http://suo.ieee.org/ontology/msg05471.html
  15. http://suo.ieee.org/ontology/msg05472.html
  16. http://suo.ieee.org/ontology/msg05473.html
  17. http://suo.ieee.org/ontology/msg05474.html
  18. http://suo.ieee.org/ontology/msg05475.html
  19. http://suo.ieee.org/ontology/msg05476.html
  20. http://suo.ieee.org/ontology/msg05479.html

NKS Forum : Feb–Jun 2004

  1. http://forum.wolframscience.com/showthread.php?postid=664#post664
  2. http://forum.wolframscience.com/showthread.php?postid=666#post666
  3. http://forum.wolframscience.com/showthread.php?postid=677#post677
  4. http://forum.wolframscience.com/showthread.php?postid=684#post684
  5. http://forum.wolframscience.com/showthread.php?postid=689#post689
  6. http://forum.wolframscience.com/showthread.php?postid=697#post697
  7. http://forum.wolframscience.com/showthread.php?postid=708#post708
  8. http://forum.wolframscience.com/showthread.php?postid=721#post721
  9. http://forum.wolframscience.com/showthread.php?postid=722#post722
  10. http://forum.wolframscience.com/showthread.php?postid=725#post725
  11. http://forum.wolframscience.com/showthread.php?postid=733#post733
  12. http://forum.wolframscience.com/showthread.php?postid=756#post756
  13. http://forum.wolframscience.com/showthread.php?postid=759#post759
  14. http://forum.wolframscience.com/showthread.php?postid=764#post764
  15. http://forum.wolframscience.com/showthread.php?postid=766#post766
  16. http://forum.wolframscience.com/showthread.php?postid=767#post767
  17. http://forum.wolframscience.com/showthread.php?postid=773#post773
  18. http://forum.wolframscience.com/showthread.php?postid=775#post775
  19. http://forum.wolframscience.com/showthread.php?postid=777#post777
  20. http://forum.wolframscience.com/showthread.php?postid=791#post791
  21. http://forum.wolframscience.com/showthread.php?postid=1458#post1458
  22. http://forum.wolframscience.com/showthread.php?postid=1461#post1461
  23. http://forum.wolframscience.com/showthread.php?postid=1463#post1463
  24. http://forum.wolframscience.com/showthread.php?postid=1464#post1464
  25. http://forum.wolframscience.com/showthread.php?postid=1467#post1467
  26. http://forum.wolframscience.com/showthread.php?postid=1469#post1469
  27. http://forum.wolframscience.com/showthread.php?postid=1470#post1470
  28. http://forum.wolframscience.com/showthread.php?postid=1471#post1471
  29. http://forum.wolframscience.com/showthread.php?postid=1473#post1473
  30. http://forum.wolframscience.com/showthread.php?postid=1475#post1475
  31. http://forum.wolframscience.com/showthread.php?postid=1479#post1479
  32. http://forum.wolframscience.com/showthread.php?postid=1489#post1489
  33. http://forum.wolframscience.com/showthread.php?postid=1490#post1490

Inquiry List : Feb–Jun 2004

  1. http://stderr.org/pipermail/inquiry/2004-February/001228.html
  2. http://stderr.org/pipermail/inquiry/2004-February/001230.html
  3. http://stderr.org/pipermail/inquiry/2004-February/001231.html
  4. http://stderr.org/pipermail/inquiry/2004-February/001232.html
  5. http://stderr.org/pipermail/inquiry/2004-February/001233.html
  6. http://stderr.org/pipermail/inquiry/2004-February/001234.html
  7. http://stderr.org/pipermail/inquiry/2004-March/001235.html
  8. http://stderr.org/pipermail/inquiry/2004-March/001236.html
  9. http://stderr.org/pipermail/inquiry/2004-March/001237.html
  10. http://stderr.org/pipermail/inquiry/2004-March/001238.html
  11. http://stderr.org/pipermail/inquiry/2004-March/001240.html
  12. http://stderr.org/pipermail/inquiry/2004-March/001242.html
  13. http://stderr.org/pipermail/inquiry/2004-March/001243.html
  14. http://stderr.org/pipermail/inquiry/2004-March/001244.html
  15. http://stderr.org/pipermail/inquiry/2004-March/001245.html
  16. http://stderr.org/pipermail/inquiry/2004-March/001246.html
  17. http://stderr.org/pipermail/inquiry/2004-March/001247.html
  18. http://stderr.org/pipermail/inquiry/2004-March/001248.html
  19. http://stderr.org/pipermail/inquiry/2004-March/001249.html
  20. http://stderr.org/pipermail/inquiry/2004-March/001255.html
  21. http://stderr.org/pipermail/inquiry/2004-June/001630.html
  22. http://stderr.org/pipermail/inquiry/2004-June/001631.html
  23. http://stderr.org/pipermail/inquiry/2004-June/001632.html
  24. http://stderr.org/pipermail/inquiry/2004-June/001633.html
  25. http://stderr.org/pipermail/inquiry/2004-June/001634.html
  26. http://stderr.org/pipermail/inquiry/2004-June/001635.html
  27. http://stderr.org/pipermail/inquiry/2004-June/001636.html
  28. http://stderr.org/pipermail/inquiry/2004-June/001637.html
  29. http://stderr.org/pipermail/inquiry/2004-June/001638.html
  30. http://stderr.org/pipermail/inquiry/2004-June/001639.html
  31. http://stderr.org/pipermail/inquiry/2004-June/001640.html
  32. http://stderr.org/pipermail/inquiry/2004-June/001641.html
  33. http://stderr.org/pipermail/inquiry/2004-June/001642.html
Retrieved from "https://mywikibiz.com/index.php?title=Directory:Jon_Awbrey/Papers/Differential_Analytic_Turing_Automata&oldid=220126"