Difference between revisions of "Directory talk:Jon Awbrey/Papers/Peirce's 1870 Logic Of Relatives"
Jon Awbrey (talk | contribs) |
Jon Awbrey (talk | contribs) |
||
| Line 1: | Line 1: | ||
| + | '''Author: [[User:Jon Awbrey|Jon Awbrey]]''' | ||
| + | |||
| + | '''Differential logic''' is the component of logic whose object is the description of variation — for example, the aspects of change, difference, distribution, and diversity — in [[universes of discourse]] that are subject to logical description. A definition that broad naturally incorporates any study of variation by way of mathematical models, but differential logic is especially charged with the qualitative aspects of variation that pervade or precede quantitative models. To the extent that a logical inquiry makes use of a formal system, its differential component treats the principles that govern the use of a ''differential logical calculus'', that is, a formal system with the expressive capacity to describe change and diversity in a logical universe of discourse. | ||
| + | |||
| + | A simple example of a differential logical calculus is furnished by a ''[[differential propositional calculus]]''. A differential propositional calculus is a [[propositional calculus]] extended by a set of terms for describing aspects of change and difference, for example, processes that take place in a universe of discourse or transformations that map a source universe into a target universe. This augments ordinary propositional calculus in the same way that the differential calculus of Leibniz and Newton augments the analytic geometry of Descartes. | ||
| + | |||
| + | ==Quick Overview== | ||
| + | |||
| + | ===Cactus Language for Propositional Logic=== | ||
| + | |||
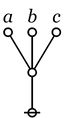
| + | The development of differential logic is greatly facilitated by having a conceptually efficient calculus in place at the level of [[boolean-valued functions]] and elementary logical propositions. A calculus that is very efficient from both conceptual and computational standpoints is based on just two types of logical connectives, both of variable <math>k\!</math>-ary scope. The formulas of this calculus map into a species of graph-theoretical structures called ''painted and rooted cacti'' (PARCs) that lend visual representation to their functional structure and smooth the path to efficient computation. | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
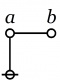
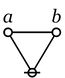
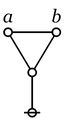
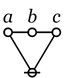
| + | | The first kind of propositional expression is a parenthesized sequence of propositional expressions, written as <math>\texttt{(} e_1 \texttt{,} e_2 \texttt{,} \ldots \texttt{,} e_{k-1} \texttt{,} e_k \texttt{)}\!</math> and read to say that exactly one of the propositions <math>e_1, e_2, \ldots, e_{k-1}, e_k\!</math> is false, in other words, that their [[minimal negation]] is true. A clause of this form maps into a PARC structure called a ''lobe'', in this case, one that is ''painted'' with the colors <math>e_1, e_2, \ldots, e_{k-1}, e_k\!</math> as shown below. | ||
| + | |} | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Cactus Graph Lobe Connective.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
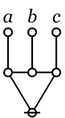
| + | | The second kind of propositional expression is a concatenated sequence of propositional expressions, written as <math>e_1\ e_2\ \ldots\ e_{k-1}\ e_k\!</math> and read to say that all of the propositions <math>e_1, e_2, \ldots, e_{k-1}, e_k\!</math> are true, in other words, that their [[logical conjunction]] is true. A clause of this form maps into a PARC structure called a ''node'', in this case, one that is ''painted'' with the colors <math>e_1, e_2, \ldots, e_{k-1}, e_k\!</math> as shown below. | ||
| + | |} | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Cactus Graph Node Connective.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | All other propositional connectives can be obtained through combinations of these two forms. Strictly speaking, the parenthesized form is sufficient to define the concatenated form, making the latter formally dispensable, but it is convenient to maintain it as a concise way of expressing more complicated combinations of parenthesized forms. While working with expressions solely in propositional calculus, it is easiest to use plain parentheses for logical connectives. In contexts where ordinary parentheses are needed for other purposes an alternate typeface <math>\texttt{(} \ldots \texttt{)}\!</math> may be used for logical operators. | ||
| + | |||
| + | Table 1 collects a sample of basic propositional forms as expressed in terms of cactus language connectives. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Table 1.}~~\text{Syntax and Semantics of a Calculus for Propositional Logic}\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | <math>\text{Graph}\!</math> | ||
| + | | <math>\text{Expression}~\!</math> | ||
| + | | <math>\text{Interpretation}\!</math> | ||
| + | | <math>\text{Other Notations}\!</math> | ||
| + | |- | ||
| + | | height="100px" | [[Image:Rooted Node.jpg|20px]] | ||
| + | | <math>~\!</math> | ||
| + | | <math>\mathrm{true}\!</math> | ||
| + | | <math>1\!</math> | ||
| + | |- | ||
| + | | height="100px" | [[Image:Rooted Edge.jpg|20px]] | ||
| + | | <math>\texttt{(}~\texttt{)}\!</math> | ||
| + | | <math>\mathrm{false}\!</math> | ||
| + | | <math>0\!</math> | ||
| + | |- | ||
| + | | height="100px" | [[Image:Cactus A Big.jpg|20px]] | ||
| + | | <math>a\!</math> | ||
| + | | <math>a\!</math> | ||
| + | | <math>a\!</math> | ||
| + | |- | ||
| + | | height="120px" | [[Image:Cactus (A) Big.jpg|20px]] | ||
| + | | <math>\texttt{(} a \texttt{)}\!</math> | ||
| + | | <math>\mathrm{not}~ a\!</math> | ||
| + | | <math>\lnot a \quad \bar{a} \quad \tilde{a} \quad a^\prime~\!</math> | ||
| + | |- | ||
| + | | height="100px" | [[Image:Cactus ABC Big.jpg|50px]] | ||
| + | | <math>a ~ b ~ c\!</math> | ||
| + | | <math>a ~\mathrm{and}~ b ~\mathrm{and}~ c\!</math> | ||
| + | | <math>a \land b \land c\!</math> | ||
| + | |- | ||
| + | | height="160px" | [[Image:Cactus ((A)(B)(C)) Big.jpg|65px]] | ||
| + | | <math>\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}\!</math> | ||
| + | | <math>a ~\mathrm{or}~ b ~\mathrm{or}~ c\!</math> | ||
| + | | <math>a \lor b \lor c\!</math> | ||
| + | |- | ||
| + | | height="120px" | [[Image:Cactus (A(B)) Big.jpg|60px]] | ||
| + | | <math>\texttt{(} a \texttt{(} b \texttt{))}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a ~\mathrm{implies}~ b | ||
| + | \\[6pt] | ||
| + | \mathrm{if}~ a ~\mathrm{then}~ b | ||
| + | \end{matrix}\!</math> | ||
| + | | <math>a \Rightarrow b\!</math> | ||
| + | |- | ||
| + | | height="120px" | [[Image:Cactus (A,B) Big ISW.jpg|65px]] | ||
| + | | <math>\texttt{(} a \texttt{,} b \texttt{)}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a ~\mathrm{not~equal~to}~ b | ||
| + | \\[6pt] | ||
| + | a ~\mathrm{exclusive~or}~ b | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a \neq b | ||
| + | \\[6pt] | ||
| + | a + b | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | height="160px" | [[Image:Cactus ((A,B)) Big.jpg|65px]] | ||
| + | | <math>\texttt{((} a \texttt{,} b \texttt{))}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a ~\mathrm{is~equal~to}~ b | ||
| + | \\[6pt] | ||
| + | a ~\mathrm{if~and~only~if}~ b | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a = b | ||
| + | \\[6pt] | ||
| + | a \Leftrightarrow b | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | height="120px" | [[Image:Cactus (A,B,C) Big.jpg|65px]] | ||
| + | | <math>\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{just~one~of} | ||
| + | \\ | ||
| + | a, b, c | ||
| + | \\ | ||
| + | \mathrm{is~false}. | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | & \bar{a} ~ b ~ c | ||
| + | \\ | ||
| + | \lor & a ~ \bar{b} ~ c | ||
| + | \\ | ||
| + | \lor & a ~ b ~ \bar{c} | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | height="160px" | [[Image:Cactus ((A),(B),(C)) Big.jpg|65px]] | ||
| + | | <math>\texttt{((} a \texttt{),(} b \texttt{),(} c \texttt{))}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{just~one~of} | ||
| + | \\ | ||
| + | a, b, c | ||
| + | \\ | ||
| + | \mathrm{is~true}. | ||
| + | \\[6pt] | ||
| + | \mathrm{partition~all} | ||
| + | \\ | ||
| + | \mathrm{into}~ a, b, c. | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | & a ~ \bar{b} ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & \bar{a} ~ b ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & \bar{a} ~ \bar{b} ~ c | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | height="160px" | [[Image:Cactus (A,(B,C)) Big.jpg|90px]] | ||
| + | | <math>\texttt{(} a \texttt{,(} b \texttt{,} c \texttt{))}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{oddly~many~of} | ||
| + | \\ | ||
| + | a, b, c | ||
| + | \\ | ||
| + | \mathrm{are~true}. | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <p><math>a + b + c\!</math></p> | ||
| + | <br> | ||
| + | <p><math>\begin{matrix} | ||
| + | & a ~ b ~ c | ||
| + | \\ | ||
| + | \lor & a ~ \bar{b} ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & \bar{a} ~ b ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & \bar{a} ~ \bar{b} ~ c | ||
| + | \end{matrix}\!</math></p> | ||
| + | |- | ||
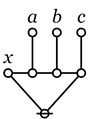
| + | | height="160px" | [[Image:Cactus (X,(A),(B),(C)) Big.jpg|90px]] | ||
| + | | <math>\texttt{(} x \texttt{,(} a \texttt{),(} b \texttt{),(} c \texttt{))}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{partition}~ x | ||
| + | \\ | ||
| + | \mathrm{into}~ a, b, c. | ||
| + | \\[6pt] | ||
| + | \mathrm{genus}~ x ~\mathrm{comprises} | ||
| + | \\ | ||
| + | \mathrm{species}~ a, b, c. | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | & \bar{x} ~ \bar{a} ~ \bar{b} ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & x ~ a ~ \bar{b} ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & x ~ \bar{a} ~ b ~ \bar{c} | ||
| + | \\ | ||
| + | \lor & x ~ \bar{a} ~ \bar{b} ~ c | ||
| + | \end{matrix}~\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | The simplest expression for logical truth is the empty word, usually denoted by <math>\boldsymbol\varepsilon\!</math> or <math>\lambda\!</math> in formal languages, where it forms the identity element for concatenation. To make it visible in context, it may be denoted by the equivalent expression <math>{}^{\backprime\backprime} \texttt{((}~\texttt{))} {}^{\prime\prime},\!</math> or, especially if operating in an algebraic context, by a simple <math>{}^{\backprime\backprime} 1 {}^{\prime\prime}.\!</math> Also when working in an algebraic mode, the plus sign <math>{}^{\backprime\backprime} + {}^{\prime\prime}\!</math> may be used for [[exclusive disjunction]]. For example, we have the following paraphrases of algebraic expressions by means of parenthesized expressions: | ||
| + | |||
| + | {| align="center" cellpadding="6" style="text-align:center" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a + b | ||
| + | & = & | ||
| + | \texttt{(} a \texttt{,} b \texttt{)} | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a + b + c | ||
| + | & = & | ||
| + | \texttt{(} a \texttt{,(} b \texttt{,} c \texttt{))} | ||
| + | & = & | ||
| + | \texttt{((} a \texttt{,} b \texttt{),} c \texttt{)} | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
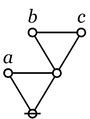
| + | It is important to note that the last expressions are not equivalent to the 3-place parenthesis <math>\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}.\!</math> | ||
| + | |||
| + | ===Differential Expansions of Propositions=== | ||
| + | |||
| + | ====Bird's Eye View==== | ||
| + | |||
| + | An efficient calculus for the realm of logic represented by boolean functions and elementary propositions makes it feasible to compute the finite differences and the differentials of those functions and propositions. | ||
| + | |||
| + | For example, consider a proposition of the form <math>{}^{\backprime\backprime} \, p ~\mathrm{and}~ q \, {}^{\prime\prime}\!</math> that is graphed as two letters attached to a root node: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Cactus Graph Existential P And Q.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | Written as a string, this is just the concatenation <math>p~q\!</math>. | ||
| + | |||
| + | The proposition <math>pq\!</math> may be taken as a boolean function <math>f(p, q)\!</math> having the abstract type <math>f : \mathbb{B} \times \mathbb{B} \to \mathbb{B},\!</math> where <math>\mathbb{B} = \{ 0, 1 \}~\!</math> is read in such a way that <math>0\!</math> means <math>\mathrm{false}\!</math> and <math>1\!</math> means <math>\mathrm{true}.\!</math> | ||
| + | |||
| + | Imagine yourself standing in a fixed cell of the corresponding venn diagram, say, the cell where the proposition <math>pq\!</math> is true, as shown in the following Figure: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Venn Diagram P And Q.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | Now ask yourself: What is the value of the proposition <math>pq\!</math> at a distance of <math>\mathrm{d}p\!</math> and <math>\mathrm{d}q\!</math> from the cell <math>pq\!</math> where you are standing? | ||
| + | |||
| + | Don't think about it — just compute: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Cactus Graph (P,dP)(Q,dQ).jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | The cactus formula <math>\texttt{(p, dp)(q, dq)}\!</math> and its corresponding graph arise by substituting <math>p + \mathrm{d}p\!</math> for <math>p\!</math> and <math>q + \mathrm{d}q\!</math> for <math>q\!</math> in the boolean product or logical conjunction <math>pq\!</math> and writing the result in the two dialects of cactus syntax. This follows from the fact that the boolean sum <math>p + \mathrm{d}p\!</math> is equivalent to the logical operation of exclusive disjunction, which parses to a cactus graph of the following form: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Cactus Graph (P,dP) ISW.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | Next question: What is the difference between the value of the proposition <math>pq\!</math> over there, at a distance of <math>\mathrm{d}p\!</math> and <math>\mathrm{d}q,\!</math> and the value of the proposition <math>pq\!</math> where you are standing, all expressed in the form of a general formula, of course? Here is the appropriate formulation: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Cactus Graph ((P,dP)(Q,dQ),PQ).jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | There is one thing that I ought to mention at this point: Computed over <math>\mathbb{B},\!</math> plus and minus are identical operations. This will make the relation between the differential and the integral parts of the appropriate calculus slightly stranger than usual, but we will get into that later. | ||
| + | |||
| + | Last question, for now: What is the value of this expression from your current standpoint, that is, evaluated at the point where <math>pq\!</math> is true? Well, substituting <math>1\!</math> for <math>p\!</math> and <math>1\!</math> for <math>q\!</math> in the graph amounts to erasing the labels <math>p\!</math> and <math>q\!,\!</math> as shown here: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Cactus Graph (( ,dP)( ,dQ), ).jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | And this is equivalent to the following graph: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Cactus Graph ((dP)(dQ)) ISW.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | We have just met with the fact that the differential of the '''''and''''' is the '''''or''''' of the differentials. | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center; width:90%" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | p ~\mathrm{and}~ q | ||
| + | & \quad & | ||
| + | \xrightarrow{\quad\mathrm{Diff}\quad} | ||
| + | & \quad & | ||
| + | \mathrm{d}p ~\mathrm{or}~ \mathrm{d}q | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Cactus Graph PQ Diff ((dP)(dQ)).jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | It will be necessary to develop a more refined analysis of that statement directly, but that is roughly the nub of it. | ||
| + | |||
| + | If the form of the above statement reminds you of De Morgan's rule, it is no accident, as differentiation and negation turn out to be closely related operations. Indeed, one can find discussions of logical difference calculus in the Boole–De Morgan correspondence and Peirce also made use of differential operators in a logical context, but the exploration of these ideas has been hampered by a number of factors, not the least of which has been the lack of a syntax that was adequate to handle the complexity of expressions that evolve. | ||
| + | |||
| + | ====Worm's Eye View==== | ||
| + | |||
| + | Let's run through the initial example again, this time attempting to interpret the formulas that develop at each stage along the way. We begin with a proposition or a boolean function <math>f(p, q) = pq.\!</math> | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Venn Diagram F = P And Q ISW.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Cactus Graph F = P And Q ISW.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | A function like this has an abstract type and a concrete type. The abstract type is what we invoke when we write things like <math>f : \mathbb{B} \times \mathbb{B} \to \mathbb{B}\!</math> or <math>f : \mathbb{B}^2 \to \mathbb{B}.\!</math> The concrete type takes into account the qualitative dimensions or the “units” of the case, which can be explained as follows. | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | Let <math>P\!</math> be the set of values <math>\{ \texttt{(} p \texttt{)},~ p \} ~=~ \{ \mathrm{not}~ p,~ p \} ~\cong~ \mathbb{B}.\!</math> | ||
| + | |- | ||
| + | | Let <math>Q\!</math> be the set of values <math>\{ \texttt{(} q \texttt{)},~ q \} ~=~ \{ \mathrm{not}~ q,~ q \} ~\cong~ \mathbb{B}.\!</math> | ||
| + | |} | ||
| + | |||
| + | Then interpret the usual propositions about <math>p, q\!</math> as functions of the concrete type <math>f : P \times Q \to \mathbb{B}.\!</math> | ||
| + | |||
| + | We are going to consider various ''operators'' on these functions. Here, an operator <math>\mathrm{F}\!</math> is a function that takes one function <math>f\!</math> into another function <math>\mathrm{F}f.\!</math> | ||
| + | |||
| + | The first couple of operators that we need to consider are logical analogues of the pair that play a founding role in the classical finite difference calculus, namely: | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | The ''difference operator'' <math>\Delta,\!</math> written here as <math>\mathrm{D}.\!</math> | ||
| + | |- | ||
| + | | The ''enlargement operator'' <math>\Epsilon,\!</math> written here as <math>\mathrm{E}.\!</math> | ||
| + | |} | ||
| + | |||
| + | These days, <math>\mathrm{E}\!</math> is more often called the ''shift operator''. | ||
| + | |||
| + | In order to describe the universe in which these operators operate, it is necessary to enlarge the original universe of discourse. Starting from the initial space <math>X = P \times Q,\!</math> its ''(first order) differential extension'' <math>\mathrm{E}X\!</math> is constructed according to the following specifications: | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | | ||
| + | <math>\begin{array}{rcc} | ||
| + | \mathrm{E}X & = & X \times \mathrm{d}X | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | where: | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | | ||
| + | <math>\begin{array}{rcc} | ||
| + | X | ||
| + | & = & | ||
| + | P \times Q | ||
| + | \\[4pt] | ||
| + | \mathrm{d}X | ||
| + | & = & | ||
| + | \mathrm{d}P \times \mathrm{d}Q | ||
| + | \\[4pt] | ||
| + | \mathrm{d}P | ||
| + | & = & | ||
| + | \{ \texttt{(} \mathrm{d}p \texttt{)},~ \mathrm{d}p \} | ||
| + | \\[4pt] | ||
| + | \mathrm{d}Q | ||
| + | & = & | ||
| + | \{ \texttt{(} \mathrm{d}q \texttt{)},~ \mathrm{d}q \} | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | The interpretations of these new symbols can be diverse, but the easiest option for now is just to say that <math>\mathrm{d}p\!</math> means “change <math>p\!</math>” and <math>\mathrm{d}q\!</math> means “change <math>q\!</math>”. | ||
| + | |||
| + | Drawing a venn diagram for the differential extension <math>\mathrm{E}X = X \times \mathrm{d}X\!</math> requires four logical dimensions, <math>P, Q, \mathrm{d}P, \mathrm{d}Q,\!</math> but it is possible to project a suggestion of what the differential features <math>\mathrm{d}p\!</math> and <math>\mathrm{d}q\!</math> are about on the 2-dimensional base space <math>X = P \times Q\!</math> by drawing arrows that cross the boundaries of the basic circles in the venn diagram for <math>X,\!</math> reading an arrow as <math>\mathrm{d}p\!</math> if it crosses the boundary between <math>p\!</math> and <math>\texttt{(} p \texttt{)}\!</math> in either direction and reading an arrow as <math>\mathrm{d}q\!</math> if it crosses the boundary between <math>q\!</math> and <math>\texttt{(} q \texttt{)}\!</math> in either direction. | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Venn Diagram P Q dP dQ.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | Propositions are formed on differential variables, or any combination of ordinary logical variables and differential logical variables, in the same ways that propositions are formed on ordinary logical variables alone. For example, the proposition <math>\texttt{(} \mathrm{d}p \texttt{(} \mathrm{d}q \texttt{))}\!</math> says the same thing as <math>\mathrm{d}p \Rightarrow \mathrm{d}q,\!</math> in other words, that there is no change in <math>p\!</math> without a change in <math>q.\!</math> | ||
| + | |||
| + | Given the proposition <math>f(p, q)\!</math> over the space <math>X = P \times Q,\!</math> the ''(first order) enlargement'' of <math>f\!</math> is the proposition <math>\mathrm{E}f\!</math> over the differential extension <math>\mathrm{E}X\!</math> that is defined by the | ||
| + | following formula: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) | ||
| + | & = & | ||
| + | f(p + \mathrm{d}p,~ q + \mathrm{d}q) | ||
| + | & = & | ||
| + | f( \texttt{(} p, \mathrm{d}p \texttt{)},~ \texttt{(} q, \mathrm{d}q \texttt{)} ) | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | In the example <math>f(p, q) = pq,\!</math> the enlargement <math>\mathrm{E}f\!</math> is computed as follows: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) | ||
| + | & = & | ||
| + | (p + \mathrm{d}p)(q + \mathrm{d}q) | ||
| + | & = & | ||
| + | \texttt{(} p, \mathrm{d}p \texttt{)(} q, \mathrm{d}q \texttt{)} | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | [[Image:Cactus Graph Ef = (P,dP)(Q,dQ).jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | Given the proposition <math>f(p, q)\!</math> over <math>X = P \times Q,\!</math> the ''(first order) difference'' of <math>f\!</math> is the proposition <math>\mathrm{D}f~\!</math> over <math>\mathrm{E}X\!</math> that is defined by the formula <math>\mathrm{D}f = \mathrm{E}f - f,\!</math> or, written out in full: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{D}f(p, q, \mathrm{d}p, \mathrm{d}q) | ||
| + | & = & | ||
| + | f(p + \mathrm{d}p,~ q + \mathrm{d}q) - f(p, q) | ||
| + | & = & | ||
| + | \texttt{(} f( \texttt{(} p, \mathrm{d}p \texttt{)},~ \texttt{(} q, \mathrm{d}q \texttt{)} ),~ f(p, q) \texttt{)} | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | In the example <math>f(p, q) = pq,\!</math> the difference <math>\mathrm{D}f~\!</math> is computed as follows: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{D}f(p, q, \mathrm{d}p, \mathrm{d}q) | ||
| + | & = & | ||
| + | (p + \mathrm{d}p)(q + \mathrm{d}q) - pq | ||
| + | & = & | ||
| + | \texttt{((} p, \mathrm{d}p \texttt{)(} q, \mathrm{d}q \texttt{)}, pq \texttt{)} | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | [[Image:Cactus Graph Df = ((P,dP)(Q,dQ),PQ).jpg|500px]] | ||
| + | |} | ||
| + | |||
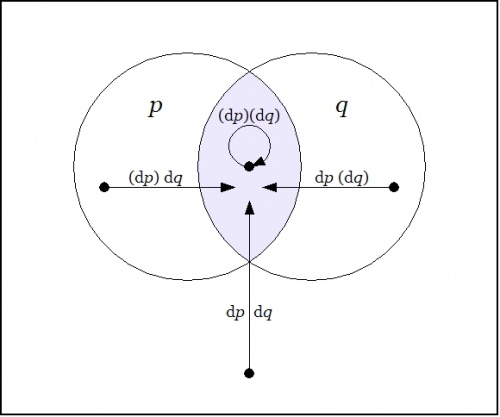
| + | We did not yet go through the trouble to interpret this (first order) ''difference of conjunction'' fully, but were happy simply to evaluate it with respect to a single location in the universe of discourse, namely, at the point picked out by the singular proposition <math>pq,\!</math> that is, at the place where <math>p = 1\!</math> and <math>q = 1.\!</math> This evaluation is written in the form <math>\mathrm{D}f|_{pq}\!</math> or <math>\mathrm{D}f|_{(1, 1)},\!</math> and we arrived at the locally applicable law that is stated and illustrated as follows: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | | ||
| + | <math>f(p, q) ~=~ pq ~=~ p ~\mathrm{and}~ q \quad \Rightarrow \quad \mathrm{D}f|_{pq} ~=~ \texttt{((} \mathrm{dp} \texttt{)(} \mathrm{d}q \texttt{))} ~=~ \mathrm{d}p ~\mathrm{or}~ \mathrm{d}q\!</math> | ||
| + | |- | ||
| + | | [[Image:Venn Diagram PQ Difference Conj At Conj.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Cactus Graph PQ Difference Conj At Conj.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | The picture shows the analysis of the inclusive disjunction <math>\texttt{((} \mathrm{d}p \texttt{)(} \mathrm{d}q \texttt{))}\!</math> into the following exclusive disjunction: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{d}p ~\texttt{(} \mathrm{d}q \texttt{)} | ||
| + | & + & | ||
| + | \texttt{(} \mathrm{d}p \texttt{)}~ \mathrm{d}q | ||
| + | & + & | ||
| + | \mathrm{d}p ~\mathrm{d}q | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | The differential proposition that results may be interpreted to say “change <math>p\!</math> or change <math>q\!</math> or both”. And this can be recognized as just what you need to do if you happen to find yourself in the center cell and require a complete and detailed description of ways to escape it. | ||
| + | |||
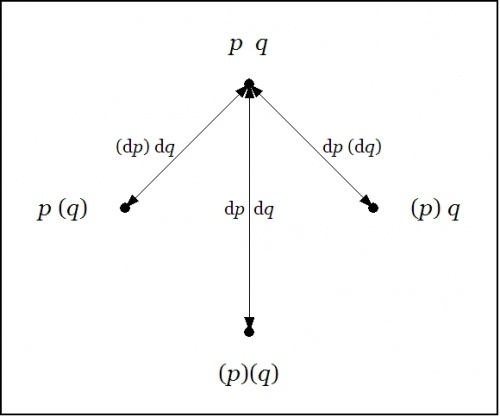
| + | Last time we computed what is variously called the ''difference map'', the ''difference proposition'', or the ''local proposition'' <math>\mathrm{D}f_x\!</math> of the proposition <math>f(p, q) = pq\!</math> at the point <math>x\!</math> where <math>p = 1\!</math> and <math>q = 1.\!</math> | ||
| + | |||
| + | In the universe <math>X = P \times Q,\!</math> the four propositions <math>pq,~ p \texttt{(} q \texttt{)},~ \texttt{(} p \texttt{)} q,~ \texttt{(} p \texttt{)(} q \texttt{)}\!</math> that indicate the “cells”, or the smallest regions of the venn diagram, are called ''singular propositions''. These serve as an alternative notation for naming the points <math>(1, 1),~ (1, 0),~ (0, 1),~ (0, 0),\!</math> respectively. | ||
| + | |||
| + | Thus we can write <math>\mathrm{D}f_x = \mathrm{D}f|x = \mathrm{D}f|(1, 1) = \mathrm{D}f|pq,\!</math> so long as we know the frame of reference in force. | ||
| + | |||
| + | In the example <math>f(p, q) = pq,\!</math> the value of the difference proposition <math>\mathrm{D}f_x\!</math> at each of the four points in <math>x \in X\!</math> may be computed in graphical fashion as shown below: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Cactus Graph Df = ((P,dP)(Q,dQ),PQ).jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Cactus Graph Df@PQ = ((dP)(dQ)).jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Cactus Graph Df@P(Q) = (dP)dQ.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Cactus Graph Df@(P)Q = dP(dQ) ISW Alt.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Cactus Graph Df@(P)(Q) = dP dQ.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | The easy way to visualize the values of these graphical expressions is just to notice the following equivalents: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Cactus Graph Lobe Rule.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Cactus Graph Spike Rule.jpg|500px]] | ||
| + | |} | ||
| + | |||
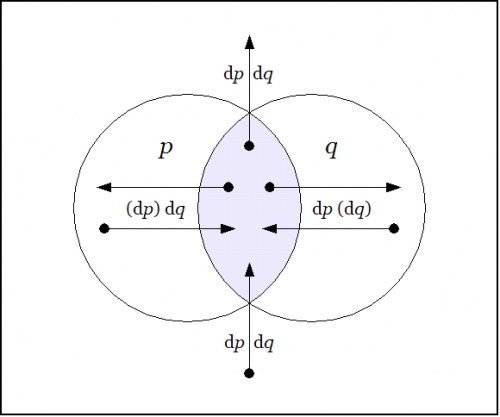
| + | Laying out the arrows on the augmented venn diagram, one gets a picture of a ''differential vector field''. | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Venn Diagram PQ Difference Conj.jpg|500px]] | ||
| + | |} | ||
| + | |||
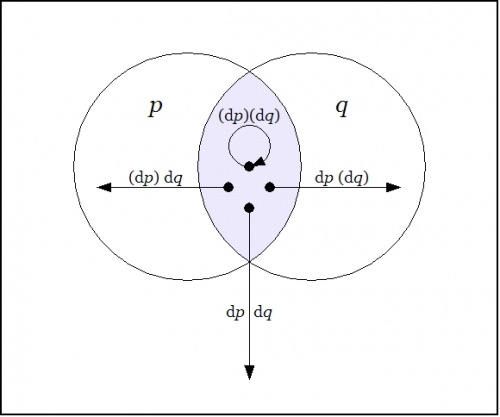
| + | The Figure shows the points of the extended universe <math>\mathrm{E}X = P \times Q \times \mathrm{d}P \times \mathrm{d}Q\!</math> that are indicated by the difference map <math>\mathrm{D}f : \mathrm{E}X \to \mathbb{B},\!</math> namely, the following six points or singular propositions:: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | | ||
| + | <math>\begin{array}{rcccc} | ||
| + | 1. & p & q & \mathrm{d}p & \mathrm{d}q | ||
| + | \\ | ||
| + | 2. & p & q & \mathrm{d}p & (\mathrm{d}q) | ||
| + | \\ | ||
| + | 3. & p & q & (\mathrm{d}p) & \mathrm{d}q | ||
| + | \\ | ||
| + | 4. & p & (q) & (\mathrm{d}p) & \mathrm{d}q | ||
| + | \\ | ||
| + | 5. & (p) & q & \mathrm{d}p & (\mathrm{d}q) | ||
| + | \\ | ||
| + | 6. & (p) & (q) & \mathrm{d}p & \mathrm{d}q | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | The information borne by <math>\mathrm{D}f~\!</math> should be clear enough from a survey of these six points — they tell you what you have to do from each point of <math>X\!</math> in order to change the value borne by <math>f(p, q),\!</math> that is, the move you have to make in order to reach a point where the value of the proposition <math>f(p, q)\!</math> is different from what it is where you started. | ||
| + | |||
| + | We have been studying the action of the difference operator <math>\mathrm{D}\!</math> on propositions of the form <math>f : P \times Q \to \mathbb{B},\!</math> as illustrated by the example <math>f(p, q) = pq\!</math> that is known in logic as the conjunction of <math>p\!</math> and <math>q.\!</math> The resulting difference map <math>\mathrm{D}f~\!</math> is a (first order) differential proposition, that is, a proposition of the form <math>\mathrm{D}f : P \times Q \times \mathrm{d}P \times \mathrm{d}Q \to \mathbb{B}.\!</math> | ||
| + | |||
| + | Abstracting from the augmented venn diagram that shows how the ''models'' or ''satisfying interpretations'' of <math>\mathrm{D}f~\!</math> distribute over the extended universe of discourse <math>\mathrm{E}X = P \times Q \times \mathrm{d}P \times \mathrm{d}Q,\!</math> the difference map <math>\mathrm{D}f~\!</math> can be represented in the form of a ''digraph'' or ''directed graph'', one whose points are labeled with the elements of <math>X = P \times Q\!</math> and whose arrows are labeled with the elements of <math>\mathrm{d}X = \mathrm{d}P \times \mathrm{d}Q,\!</math> as shown in the following Figure. | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Directed Graph PQ Difference Conj.jpg|500px]] | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{array}{rcccccc} | ||
| + | f | ||
| + | & = & p & \cdot & q | ||
| + | \\[4pt] | ||
| + | \mathrm{D}f | ||
| + | & = & p & \cdot & q & \cdot & ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | & + & p & \cdot & (q) & \cdot & ~(\mathrm{d}p)~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | & + & (p) & \cdot & q & \cdot & ~~\mathrm{d}p~(\mathrm{d}q)~ | ||
| + | \\[4pt] | ||
| + | & + & (p) & \cdot & (q) & \cdot & ~~\mathrm{d}p~~\mathrm{d}q~~ | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | Any proposition worth its salt can be analyzed from many different points of view, any one of which has the potential to reveal an unsuspected aspect of the proposition's meaning. We will encounter more and more of these alternative readings as we go. | ||
| + | |||
| + | The ''enlargement'' or ''shift'' operator <math>\mathrm{E}\!</math> exhibits a wealth of interesting and useful properties in its own right, so it pays to examine a few of the more salient features that play out on the surface of our initial example, <math>f(p, q) = pq.\!</math> | ||
| + | |||
| + | A suitably generic definition of the extended universe of discourse is afforded by the following set-up: | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | | ||
| + | <math>\begin{array}{lccl} | ||
| + | \text{Let} & | ||
| + | X | ||
| + | & = & | ||
| + | X_1 \times \ldots \times X_k. | ||
| + | \\[6pt] | ||
| + | \text{Let} & | ||
| + | \mathrm{d}X | ||
| + | & = & | ||
| + | \mathrm{d}X_1 \times \ldots \times \mathrm{d}X_k. | ||
| + | \\[6pt] | ||
| + | \text{Then} & | ||
| + | \mathrm{E}X | ||
| + | & = & | ||
| + | X \times \mathrm{d}X | ||
| + | \\[6pt] | ||
| + | & | ||
| + | & = & X_1 \times \ldots \times X_k ~\times~ \mathrm{d}X_1 \times \ldots \times \mathrm{d}X_k | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | For a proposition of the form <math>f : X_1 \times \ldots \times X_k \to \mathbb{B},\!</math> the ''(first order) enlargement'' of <math>f\!</math> is the proposition <math>\mathrm{E}f : \mathrm{E}X \to \mathbb{B}\!</math> that is defined by the following equation: | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | | ||
| + | <math>\begin{array}{l} | ||
| + | \mathrm{E}f(x_1, \ldots, x_k, \mathrm{d}x_1, \ldots, \mathrm{d}x_k) | ||
| + | \\[6pt] | ||
| + | = \quad f(x_1 + \mathrm{d}x_1, \ldots, x_k + \mathrm{d}x_k) | ||
| + | \\[6pt] | ||
| + | = \quad f( \texttt{(} x_1, \mathrm{d}x_1 \texttt{)}, \ldots, \texttt{(} x_k, \mathrm{d}x_k \texttt{)} ) | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | The ''differential variables'' <math>\mathrm{d}x_j\!</math> are boolean variables of the same basic type as the ordinary variables <math>x_j.\!</math> Although it is conventional to distinguish the (first order) differential variables with the operative prefix “<math>\mathrm{d}\!</math>” this way of notating differential variables is entirely optional. It is their existence in particular relations to the initial variables, not their names, that defines them as differential variables. | ||
| + | |||
| + | In the example of logical conjunction, <math>f(p, q) = pq,\!</math> the enlargement <math>\mathrm{E}f\!</math> is formulated as follows: | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | | ||
| + | <math>\begin{array}{l} | ||
| + | \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) | ||
| + | \\[6pt] | ||
| + | = \quad (p + \mathrm{d}p)(q + \mathrm{d}q) | ||
| + | \\[6pt] | ||
| + | = \quad \texttt{(} p, \mathrm{d}p \texttt{)(} q, \mathrm{d}q \texttt{)} | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | Given that this expression uses nothing more than the boolean ring operations of addition and multiplication, it is permissible to “multiply things out” in the usual manner to arrive at the following result: | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) | ||
| + | & = & | ||
| + | p~q | ||
| + | & + & | ||
| + | p~\mathrm{d}q | ||
| + | & + & | ||
| + | q~\mathrm{d}p | ||
| + | & + & | ||
| + | \mathrm{d}p~\mathrm{d}q | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
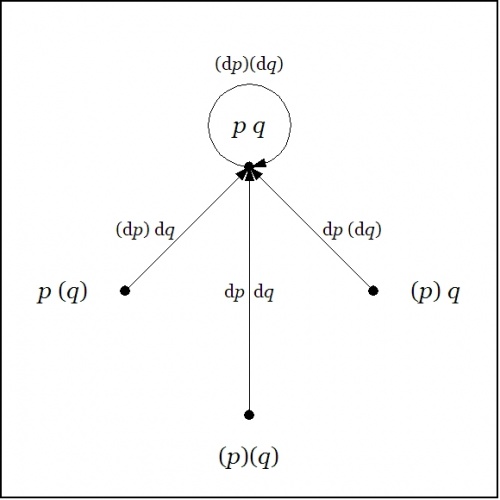
| + | To understand what the ''enlarged'' or ''shifted'' proposition means in logical terms, it serves to go back and analyze the above expression for <math>\mathrm{E}f\!</math> in the same way that we did for <math>\mathrm{D}f.\!</math> Toward that end, the value of <math>\mathrm{E}f_x\!</math> at each <math>x \in X\!</math> may be computed in graphical fashion as shown below: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Cactus Graph Ef = (P,dP)(Q,dQ).jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Cactus Graph Ef@PQ = (dP)(dQ).jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Cactus Graph Ef@P(Q) = (dP)dQ.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Cactus Graph Ef@(P)Q = dP(dQ).jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Cactus Graph Ef@(P)(Q) = dP dQ.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | Given the data that develops in this form of analysis, the disjoined ingredients can now be folded back into a boolean expansion or a disjunctive normal form (DNF) that is equivalent to the enlarged proposition <math>\mathrm{E}f.\!</math> | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{E}f | ||
| + | & = & | ||
| + | pq \cdot \mathrm{E}f_{pq} | ||
| + | & + & | ||
| + | p(q) \cdot \mathrm{E}f_{p(q)} | ||
| + | & + & | ||
| + | (p)q \cdot \mathrm{E}f_{(p)q} | ||
| + | & + & | ||
| + | (p)(q) \cdot \mathrm{E}f_{(p)(q)} | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | Here is a summary of the result, illustrated by means of a digraph picture, where the “no change” element <math>(\mathrm{d}p)(\mathrm{d}q)\!</math> is drawn as a loop at the point <math>p~q.\!</math> | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Directed Graph PQ Enlargement Conj.jpg|500px]] | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{array}{rcccccc} | ||
| + | f | ||
| + | & = & p & \cdot & q | ||
| + | \\[4pt] | ||
| + | \mathrm{E}f | ||
| + | & = & p & \cdot & q & \cdot & (\mathrm{d}p)(\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | & + & p & \cdot & (q) & \cdot & (\mathrm{d}p)~\mathrm{d}q~ | ||
| + | \\[4pt] | ||
| + | & + & (p) & \cdot & q & \cdot & ~\mathrm{d}p~(\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | & + & (p) & \cdot & (q) & \cdot & ~\mathrm{d}p~~\mathrm{d}q~\end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | We may understand the enlarged proposition <math>\mathrm{E}f\!</math> as telling us all the different ways to reach a model of the proposition <math>f\!</math> from each point of the universe <math>X.\!</math> | ||
| + | |||
| + | ==Propositional Forms on Two Variables== | ||
| + | |||
| + | To broaden our experience with simple examples, let us examine the sixteen functions of concrete type <math>P \times Q \to \mathbb{B}\!</math> and abstract type <math>\mathbb{B} \times \mathbb{B} \to \mathbb{B}.\!</math> A few Tables are set here that detail the actions of <math>\mathrm{E}\!</math> and <math>\mathrm{D}\!</math> on each of these functions, allowing us to view the results in several different ways. | ||
| + | |||
| + | Tables A1 and A2 show two ways of arranging the 16 boolean functions on two variables, giving equivalent expressions for each function in several different systems of notation. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Table A1.}~~\text{Propositional Forms on Two Variables}\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | width="15%" | | ||
| + | <p><math>\mathcal{L}_1\!</math></p> | ||
| + | <p><math>\text{Decimal}\!</math></p> | ||
| + | | width="15%" | | ||
| + | <p><math>\mathcal{L}_2\!</math></p> | ||
| + | <p><math>\text{Binary}\!</math></p> | ||
| + | | width="15%" | | ||
| + | <p><math>\mathcal{L}_3\!</math></p> | ||
| + | <p><math>\text{Vector}\!</math></p> | ||
| + | | width="15%" | | ||
| + | <p><math>\mathcal{L}_4\!</math></p> | ||
| + | <p><math>\text{Cactus}\!</math></p> | ||
| + | | width="25%" | | ||
| + | <p><math>\mathcal{L}_5\!</math></p> | ||
| + | <p><math>\text{English}\!</math></p> | ||
| + | | width="15%" | | ||
| + | <p><math>\mathcal{L}_6~\!</math></p> | ||
| + | <p><math>\text{Ordinary}\!</math></p> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | | ||
| + | | align="right" | <math>p\colon\!</math> | ||
| + | | <math>1~1~0~0\!</math> | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- style="background:#f0f0ff" | ||
| + | | | ||
| + | | align="right" | <math>q\colon\!</math> | ||
| + | | <math>1~0~1~0\!</math> | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_0 | ||
| + | \\[4pt] | ||
| + | f_1 | ||
| + | \\[4pt] | ||
| + | f_2 | ||
| + | \\[4pt] | ||
| + | f_3 | ||
| + | \\[4pt] | ||
| + | f_4 | ||
| + | \\[4pt] | ||
| + | f_5 | ||
| + | \\[4pt] | ||
| + | f_6 | ||
| + | \\[4pt] | ||
| + | f_7 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_{0000} | ||
| + | \\[4pt] | ||
| + | f_{0001} | ||
| + | \\[4pt] | ||
| + | f_{0010} | ||
| + | \\[4pt] | ||
| + | f_{0011} | ||
| + | \\[4pt] | ||
| + | f_{0100} | ||
| + | \\[4pt] | ||
| + | f_{0101} | ||
| + | \\[4pt] | ||
| + | f_{0110} | ||
| + | \\[4pt] | ||
| + | f_{0111} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0~0~0~0 | ||
| + | \\[4pt] | ||
| + | 0~0~0~1 | ||
| + | \\[4pt] | ||
| + | 0~0~1~0 | ||
| + | \\[4pt] | ||
| + | 0~0~1~1 | ||
| + | \\[4pt] | ||
| + | 0~1~0~0 | ||
| + | \\[4pt] | ||
| + | 0~1~0~1 | ||
| + | \\[4pt] | ||
| + | 0~1~1~0 | ||
| + | \\[4pt] | ||
| + | 0~1~1~1 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | (p)~ ~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | ~ ~(q) | ||
| + | \\[4pt] | ||
| + | (p,~q) | ||
| + | \\[4pt] | ||
| + | (p~~q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \text{false} | ||
| + | \\[4pt] | ||
| + | \text{neither}~ p ~\text{nor}~ q | ||
| + | \\[4pt] | ||
| + | q ~\text{without}~ p | ||
| + | \\[4pt] | ||
| + | \text{not}~ p | ||
| + | \\[4pt] | ||
| + | p ~\text{without}~ q | ||
| + | \\[4pt] | ||
| + | \text{not}~ q | ||
| + | \\[4pt] | ||
| + | p ~\text{not equal to}~ q | ||
| + | \\[4pt] | ||
| + | \text{not both}~ p ~\text{and}~ q | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0 | ||
| + | \\[4pt] | ||
| + | \lnot p \land \lnot q | ||
| + | \\[4pt] | ||
| + | \lnot p \land q | ||
| + | \\[4pt] | ||
| + | \lnot p | ||
| + | \\[4pt] | ||
| + | p \land \lnot q | ||
| + | \\[4pt] | ||
| + | \lnot q | ||
| + | \\[4pt] | ||
| + | p \ne q | ||
| + | \\[4pt] | ||
| + | \lnot p \lor \lnot q | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_8 | ||
| + | \\[4pt] | ||
| + | f_9 | ||
| + | \\[4pt] | ||
| + | f_{10} | ||
| + | \\[4pt] | ||
| + | f_{11} | ||
| + | \\[4pt] | ||
| + | f_{12} | ||
| + | \\[4pt] | ||
| + | f_{13} | ||
| + | \\[4pt] | ||
| + | f_{14} | ||
| + | \\[4pt] | ||
| + | f_{15} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_{1000} | ||
| + | \\[4pt] | ||
| + | f_{1001} | ||
| + | \\[4pt] | ||
| + | f_{1010} | ||
| + | \\[4pt] | ||
| + | f_{1011} | ||
| + | \\[4pt] | ||
| + | f_{1100} | ||
| + | \\[4pt] | ||
| + | f_{1101} | ||
| + | \\[4pt] | ||
| + | f_{1110} | ||
| + | \\[4pt] | ||
| + | f_{1111} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 1~0~0~0 | ||
| + | \\[4pt] | ||
| + | 1~0~0~1 | ||
| + | \\[4pt] | ||
| + | 1~0~1~0 | ||
| + | \\[4pt] | ||
| + | 1~0~1~1 | ||
| + | \\[4pt] | ||
| + | 1~1~0~0 | ||
| + | \\[4pt] | ||
| + | 1~1~0~1 | ||
| + | \\[4pt] | ||
| + | 1~1~1~0 | ||
| + | \\[4pt] | ||
| + | 1~1~1~1 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~~p~~q~~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \\[4pt] | ||
| + | ~ ~ ~q~~ | ||
| + | \\[4pt] | ||
| + | ~(p~(q)) | ||
| + | \\[4pt] | ||
| + | ~~p~ ~ ~ | ||
| + | \\[4pt] | ||
| + | ((p)~q)~ | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \\[4pt] | ||
| + | ((~)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | p ~\text{and}~ q | ||
| + | \\[4pt] | ||
| + | p ~\text{equal to}~ q | ||
| + | \\[4pt] | ||
| + | q | ||
| + | \\[4pt] | ||
| + | \text{not}~ p ~\text{without}~ q | ||
| + | \\[4pt] | ||
| + | p | ||
| + | \\[4pt] | ||
| + | \text{not}~ q ~\text{without}~ p | ||
| + | \\[4pt] | ||
| + | p ~\text{or}~ q | ||
| + | \\[4pt] | ||
| + | \text{true} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | p \land q | ||
| + | \\[4pt] | ||
| + | p = q | ||
| + | \\[4pt] | ||
| + | q | ||
| + | \\[4pt] | ||
| + | p \Rightarrow q | ||
| + | \\[4pt] | ||
| + | p | ||
| + | \\[4pt] | ||
| + | p \Leftarrow q | ||
| + | \\[4pt] | ||
| + | p \lor q | ||
| + | \\[4pt] | ||
| + | 1 | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Table A2.}~~\text{Propositional Forms on Two Variables}\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | width="15%" | | ||
| + | <p><math>\mathcal{L}_1\!</math></p> | ||
| + | <p><math>\text{Decimal}\!</math></p> | ||
| + | | width="15%" | | ||
| + | <p><math>\mathcal{L}_2\!</math></p> | ||
| + | <p><math>\text{Binary}\!</math></p> | ||
| + | | width="15%" | | ||
| + | <p><math>\mathcal{L}_3\!</math></p> | ||
| + | <p><math>\text{Vector}\!</math></p> | ||
| + | | width="15%" | | ||
| + | <p><math>\mathcal{L}_4\!</math></p> | ||
| + | <p><math>\text{Cactus}\!</math></p> | ||
| + | | width="25%" | | ||
| + | <p><math>\mathcal{L}_5\!</math></p> | ||
| + | <p><math>\text{English}\!</math></p> | ||
| + | | width="15%" | | ||
| + | <p><math>\mathcal{L}_6~\!</math></p> | ||
| + | <p><math>\text{Ordinary}\!</math></p> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | | ||
| + | | align="right" | <math>p\colon\!</math> | ||
| + | | <math>1~1~0~0\!</math> | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- style="background:#f0f0ff" | ||
| + | | | ||
| + | | align="right" | <math>q\colon\!</math> | ||
| + | | <math>1~0~1~0\!</math> | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | <math>f_0\!</math> | ||
| + | | <math>f_{0000}\!</math> | ||
| + | | <math>0~0~0~0\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>\text{false}\!</math> | ||
| + | | <math>0\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_1 | ||
| + | \\[4pt] | ||
| + | f_2 | ||
| + | \\[4pt] | ||
| + | f_4 | ||
| + | \\[4pt] | ||
| + | f_8 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_{0001} | ||
| + | \\[4pt] | ||
| + | f_{0010} | ||
| + | \\[4pt] | ||
| + | f_{0100} | ||
| + | \\[4pt] | ||
| + | f_{1000} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0~0~0~1 | ||
| + | \\[4pt] | ||
| + | 0~0~1~0 | ||
| + | \\[4pt] | ||
| + | 0~1~0~0 | ||
| + | \\[4pt] | ||
| + | 1~0~0~0 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \text{neither}~ p ~\text{nor}~ q | ||
| + | \\[4pt] | ||
| + | q ~\text{without}~ p | ||
| + | \\[4pt] | ||
| + | p ~\text{without}~ q | ||
| + | \\[4pt] | ||
| + | p ~\text{and}~ q | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \lnot p \land \lnot q | ||
| + | \\[4pt] | ||
| + | \lnot p \land q | ||
| + | \\[4pt] | ||
| + | p \land \lnot q | ||
| + | \\[4pt] | ||
| + | p \land q | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_3 | ||
| + | \\[4pt] | ||
| + | f_{12} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_{0011} | ||
| + | \\[4pt] | ||
| + | f_{1100} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0~0~1~1 | ||
| + | \\[4pt] | ||
| + | 1~1~0~0 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \text{not}~ p | ||
| + | \\[4pt] | ||
| + | p | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \lnot p | ||
| + | \\[4pt] | ||
| + | p | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_6 | ||
| + | \\[4pt] | ||
| + | f_9 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_{0110} | ||
| + | \\[4pt] | ||
| + | f_{1001} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0~1~1~0 | ||
| + | \\[4pt] | ||
| + | 1~0~0~1 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | p ~\text{not equal to}~ q | ||
| + | \\[4pt] | ||
| + | p ~\text{equal to}~ q | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | p \ne q | ||
| + | \\[4pt] | ||
| + | p = q | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_5 | ||
| + | \\[4pt] | ||
| + | f_{10} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_{0101} | ||
| + | \\[4pt] | ||
| + | f_{1010} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0~1~0~1 | ||
| + | \\[4pt] | ||
| + | 1~0~1~0 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \text{not}~ q | ||
| + | \\[4pt] | ||
| + | q | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \lnot q | ||
| + | \\[4pt] | ||
| + | q | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_7 | ||
| + | \\[4pt] | ||
| + | f_{11} | ||
| + | \\[4pt] | ||
| + | f_{13} | ||
| + | \\[4pt] | ||
| + | f_{14} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_{0111} | ||
| + | \\[4pt] | ||
| + | f_{1011} | ||
| + | \\[4pt] | ||
| + | f_{1101} | ||
| + | \\[4pt] | ||
| + | f_{1110} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0~1~1~1 | ||
| + | \\[4pt] | ||
| + | 1~0~1~1 | ||
| + | \\[4pt] | ||
| + | 1~1~0~1 | ||
| + | \\[4pt] | ||
| + | 1~1~1~0 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p~~q)~ | ||
| + | \\[4pt] | ||
| + | ~(p~(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q)~ | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \text{not both}~ p ~\text{and}~ q | ||
| + | \\[4pt] | ||
| + | \text{not}~ p ~\text{without}~ q | ||
| + | \\[4pt] | ||
| + | \text{not}~ q ~\text{without}~ p | ||
| + | \\[4pt] | ||
| + | p ~\text{or}~ q | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \lnot p \lor \lnot q | ||
| + | \\[4pt] | ||
| + | p \Rightarrow q | ||
| + | \\[4pt] | ||
| + | p \Leftarrow q | ||
| + | \\[4pt] | ||
| + | p \lor q | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | <math>f_{15}\!</math> | ||
| + | | <math>f_{1111}\!</math> | ||
| + | | <math>1~1~1~1\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>\text{true}\!</math> | ||
| + | | <math>1\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | ===Transforms Expanded over Differential Features=== | ||
| + | |||
| + | The next four Tables expand the expressions of <math>\mathrm{E}f\!</math> and <math>\mathrm{D}f~\!</math> in two different ways, for each of the sixteen functions. Notice that the functions are given in a different order, partitioned into seven natural classes by a group action. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Table A3.}~~\mathrm{E}f ~\text{Expanded over Differential Features}~ \{ \mathrm{d}p, \mathrm{d}q \}\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | width="10%" | | ||
| + | | width="18%" | <math>f\!</math> | ||
| + | | width="18%" | | ||
| + | <p><math>\mathrm{T}_{11} f\!</math></p> | ||
| + | <p><math>\mathrm{E}f|_{\mathrm{d}p~\mathrm{d}q}\!</math></p> | ||
| + | | width="18%" | | ||
| + | <p><math>\mathrm{T}_{10} f\!</math></p> | ||
| + | <p><math>\mathrm{E}f|_{\mathrm{d}p(\mathrm{d}q)}\!</math></p> | ||
| + | | width="18%" | | ||
| + | <p><math>\mathrm{T}_{01} f\!</math></p> | ||
| + | <p><math>\mathrm{E}f|_{(\mathrm{d}p)\mathrm{d}q}\!</math></p> | ||
| + | | width="18%" | | ||
| + | <p><math>\mathrm{T}_{00} f\!</math></p> | ||
| + | <p><math>\mathrm{E}f|_{(\mathrm{d}p)(\mathrm{d}q)}\!</math></p> | ||
| + | |- | ||
| + | | <math>f_0\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_1 | ||
| + | \\[4pt] | ||
| + | f_2 | ||
| + | \\[4pt] | ||
| + | f_4 | ||
| + | \\[4pt] | ||
| + | f_8 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~p~~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | (p)(q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \\[4pt] | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_3 | ||
| + | \\[4pt] | ||
| + | f_{12} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~p~ | ||
| + | \\[4pt] | ||
| + | (p) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~p~ | ||
| + | \\[4pt] | ||
| + | (p) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_6 | ||
| + | \\[4pt] | ||
| + | f_9 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((p,~q)) | ||
| + | \\[4pt] | ||
| + | ~(p,~q)~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((p,~q)) | ||
| + | \\[4pt] | ||
| + | ~(p,~q)~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_5 | ||
| + | \\[4pt] | ||
| + | f_{10} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~q~ | ||
| + | \\[4pt] | ||
| + | (q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~q~ | ||
| + | \\[4pt] | ||
| + | (q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_7 | ||
| + | \\[4pt] | ||
| + | f_{11} | ||
| + | \\[4pt] | ||
| + | f_{13} | ||
| + | \\[4pt] | ||
| + | f_{14} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~p~~q~) | ||
| + | \\[4pt] | ||
| + | (~p~(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q~) | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((p)(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q~) | ||
| + | \\[4pt] | ||
| + | (~p~(q)) | ||
| + | \\[4pt] | ||
| + | (~p~~q~) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((p)~q~) | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \\[4pt] | ||
| + | (~p~~q~) | ||
| + | \\[4pt] | ||
| + | (~p~(q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~p~(q)) | ||
| + | \\[4pt] | ||
| + | (~p~~q~) | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q~) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~p~~q~) | ||
| + | \\[4pt] | ||
| + | (~p~(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q~) | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | <math>f_{15}\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | colspan="2" | <math>\text{Fixed Point Total}\!</math> | ||
| + | | <math>4\!</math> | ||
| + | | <math>4\!</math> | ||
| + | | <math>4\!</math> | ||
| + | | <math>16\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Table A4.}~~\mathrm{D}f ~\text{Expanded over Differential Features}~ \{ \mathrm{d}p, \mathrm{d}q \}\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | width="10%" | | ||
| + | | width="18%" | <math>f\!</math> | ||
| + | | width="18%" | | ||
| + | <math>\mathrm{D}f|_{\mathrm{d}p~\mathrm{d}q}\!</math> | ||
| + | | width="18%" | | ||
| + | <math>\mathrm{D}f|_{\mathrm{d}p(\mathrm{d}q)}\!</math> | ||
| + | | width="18%" | | ||
| + | <math>\mathrm{D}f|_{(\mathrm{d}p)\mathrm{d}q}\!</math> | ||
| + | | width="18%" | | ||
| + | <math>\mathrm{D}f|_{(\mathrm{d}p)(\mathrm{d}q)}\!</math> | ||
| + | |- | ||
| + | | <math>f_0\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_1 | ||
| + | \\[4pt] | ||
| + | f_2 | ||
| + | \\[4pt] | ||
| + | f_4 | ||
| + | \\[4pt] | ||
| + | f_8 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((p,~q)) | ||
| + | \\[4pt] | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \\[4pt] | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_3 | ||
| + | \\[4pt] | ||
| + | f_{12} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((~)) | ||
| + | \\[4pt] | ||
| + | ((~)) | ||
| + | \end{matrix}~\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((~)) | ||
| + | \\[4pt] | ||
| + | ((~)) | ||
| + | \end{matrix}~\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_6 | ||
| + | \\[4pt] | ||
| + | f_9 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((~)) | ||
| + | \\[4pt] | ||
| + | ((~)) | ||
| + | \end{matrix}~\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((~)) | ||
| + | \\[4pt] | ||
| + | ((~)) | ||
| + | \end{matrix}~\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_5 | ||
| + | \\[4pt] | ||
| + | f_{10} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((~)) | ||
| + | \\[4pt] | ||
| + | ((~)) | ||
| + | \end{matrix}~\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((~)) | ||
| + | \\[4pt] | ||
| + | ((~)) | ||
| + | \end{matrix}~\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_7 | ||
| + | \\[4pt] | ||
| + | f_{11} | ||
| + | \\[4pt] | ||
| + | f_{13} | ||
| + | \\[4pt] | ||
| + | f_{14} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p~~q)~ | ||
| + | \\[4pt] | ||
| + | ~(p~(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q)~ | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((p,~q)) | ||
| + | \\[4pt] | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~q~ | ||
| + | \\[4pt] | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \\[4pt] | ||
| + | (q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~p~ | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \\[4pt] | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | (p) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \\[4pt] | ||
| + | (~) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | <math>f_{15}\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | ===Transforms Expanded over Ordinary Features=== | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Table A5.}~~\mathrm{E}f ~\text{Expanded over Ordinary Features}~ \{ p, q \}\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | width="10%" | | ||
| + | | width="18%" | <math>f\!</math> | ||
| + | | width="18%" | <math>\mathrm{E}f|_{pq}\!</math> | ||
| + | | width="18%" | <math>\mathrm{E}f|_{p(q)}\!</math> | ||
| + | | width="18%" | <math>\mathrm{E}f|_{(p)q}\!</math> | ||
| + | | width="18%" | <math>\mathrm{E}f|_{(p)(q)}\!</math> | ||
| + | |- | ||
| + | | <math>f_0\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_1 | ||
| + | \\[4pt] | ||
| + | f_2 | ||
| + | \\[4pt] | ||
| + | f_4 | ||
| + | \\[4pt] | ||
| + | f_8 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~\mathrm{d}p~~\mathrm{d}q~ | ||
| + | \\[4pt] | ||
| + | ~\mathrm{d}p~(\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p)~\mathrm{d}q~ | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p)(\mathrm{d}q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~\mathrm{d}p~(\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | ~\mathrm{d}p~~\mathrm{d}q~ | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p)(\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p)~\mathrm{d}q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (\mathrm{d}p)~\mathrm{d}q~ | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p)(\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | ~\mathrm{d}p~~\mathrm{d}q~ | ||
| + | \\[4pt] | ||
| + | ~\mathrm{d}p~(\mathrm{d}q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (\mathrm{d}p)(\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p)~\mathrm{d}q~ | ||
| + | \\[4pt] | ||
| + | ~\mathrm{d}p~(\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | ~\mathrm{d}p~~\mathrm{d}q~ | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_3 | ||
| + | \\[4pt] | ||
| + | f_{12} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~\mathrm{d}p~ | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~\mathrm{d}p~ | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (\mathrm{d}p) | ||
| + | \\[4pt] | ||
| + | ~\mathrm{d}p~ | ||
| + | \end{matrix}~\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (\mathrm{d}p) | ||
| + | \\[4pt] | ||
| + | ~\mathrm{d}p~ | ||
| + | \end{matrix}~\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_6 | ||
| + | \\[4pt] | ||
| + | f_9 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(\mathrm{d}p,~\mathrm{d}q)~ | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p,~\mathrm{d}q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((\mathrm{d}p,~\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | ~(\mathrm{d}p,~\mathrm{d}q)~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((\mathrm{d}p,~\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | ~(\mathrm{d}p,~\mathrm{d}q)~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(\mathrm{d}p,~\mathrm{d}q)~ | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p,~\mathrm{d}q)) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_5 | ||
| + | \\[4pt] | ||
| + | f_{10} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~\mathrm{d}q~ | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | ~\mathrm{d}q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~\mathrm{d}q~ | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | ~\mathrm{d}q~ | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_7 | ||
| + | \\[4pt] | ||
| + | f_{11} | ||
| + | \\[4pt] | ||
| + | f_{13} | ||
| + | \\[4pt] | ||
| + | f_{14} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~p~~q~) | ||
| + | \\[4pt] | ||
| + | (~p~(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q~) | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)~\mathrm{d}q~) | ||
| + | \\[4pt] | ||
| + | (~\mathrm{d}p~(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | (~\mathrm{d}p~~\mathrm{d}q~) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((\mathrm{d}p)~\mathrm{d}q~) | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | (~\mathrm{d}p~~\mathrm{d}q~) | ||
| + | \\[4pt] | ||
| + | (~\mathrm{d}p~(\mathrm{d}q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~\mathrm{d}p~(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | (~\mathrm{d}p~~\mathrm{d}q~) | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)~\mathrm{d}q~) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~\mathrm{d}p~~\mathrm{d}q~) | ||
| + | \\[4pt] | ||
| + | (~\mathrm{d}p~(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)~\mathrm{d}q~) | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | <math>f_{15}\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Table A6.}~~\mathrm{D}f ~\text{Expanded over Ordinary Features}~ \{ p, q \}\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | width="10%" | | ||
| + | | width="18%" | <math>f\!</math> | ||
| + | | width="18%" | <math>\mathrm{D}f|_{pq}\!</math> | ||
| + | | width="18%" | <math>\mathrm{D}f|_{p(q)}\!</math> | ||
| + | | width="18%" | <math>\mathrm{D}f|_{(p)q}\!</math> | ||
| + | | width="18%" | <math>\mathrm{D}f|_{(p)(q)}\!</math> | ||
| + | |- | ||
| + | | <math>f_0\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_1 | ||
| + | \\[4pt] | ||
| + | f_2 | ||
| + | \\[4pt] | ||
| + | f_4 | ||
| + | \\[4pt] | ||
| + | f_8 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~~\mathrm{d}p~~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~(\mathrm{d}q)~ | ||
| + | \\[4pt] | ||
| + | ~(\mathrm{d}p)~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~~\mathrm{d}p~(\mathrm{d}q)~ | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | ~(\mathrm{d}p)~\mathrm{d}q~~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(\mathrm{d}p)~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~(\mathrm{d}q)~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | ~(\mathrm{d}p)~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~(\mathrm{d}q)~ | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~~\mathrm{d}q~~ | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_3 | ||
| + | \\[4pt] | ||
| + | f_{12} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{d}p | ||
| + | \\[4pt] | ||
| + | \mathrm{d}p | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{d}p | ||
| + | \\[4pt] | ||
| + | \mathrm{d}p | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{d}p | ||
| + | \\[4pt] | ||
| + | \mathrm{d}p | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{d}p | ||
| + | \\[4pt] | ||
| + | \mathrm{d}p | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_6 | ||
| + | \\[4pt] | ||
| + | f_9 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (\mathrm{d}p,~\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p,~\mathrm{d}q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (\mathrm{d}p,~\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p,~\mathrm{d}q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (\mathrm{d}p,~\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p,~\mathrm{d}q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (\mathrm{d}p,~\mathrm{d}q) | ||
| + | \\[4pt] | ||
| + | (\mathrm{d}p,~\mathrm{d}q) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_5 | ||
| + | \\[4pt] | ||
| + | f_{10} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{d}q | ||
| + | \\[4pt] | ||
| + | \mathrm{d}q | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{d}q | ||
| + | \\[4pt] | ||
| + | \mathrm{d}q | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{d}q | ||
| + | \\[4pt] | ||
| + | \mathrm{d}q | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{d}q | ||
| + | \\[4pt] | ||
| + | \mathrm{d}q | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_7 | ||
| + | \\[4pt] | ||
| + | f_{11} | ||
| + | \\[4pt] | ||
| + | f_{13} | ||
| + | \\[4pt] | ||
| + | f_{14} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~p~~q~) | ||
| + | \\[4pt] | ||
| + | (~p~(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q~) | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | ~(\mathrm{d}p)~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~(\mathrm{d}q)~ | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~~\mathrm{d}q~~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(\mathrm{d}p)~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~(\mathrm{d}q)~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~~\mathrm{d}p~(\mathrm{d}q)~ | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \\[4pt] | ||
| + | ~(\mathrm{d}p)~\mathrm{d}q~~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~~\mathrm{d}p~~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ~~\mathrm{d}p~(\mathrm{d}q)~ | ||
| + | \\[4pt] | ||
| + | ~(\mathrm{d}p)~\mathrm{d}q~~ | ||
| + | \\[4pt] | ||
| + | ((\mathrm{d}p)(\mathrm{d}q)) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | <math>f_{15}\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | ==Operational Representation== | ||
| + | |||
| + | If you think that I linger in the realm of logical difference calculus out of sheer vacillation about getting down to the differential proper, it is probably out of a prior expectation that you derive from the art or the long-engrained practice of real analysis. But the fact is that ordinary calculus only rushes on to the sundry orders of approximation because the strain of comprehending the full import of <math>\mathrm{E}\!</math> and <math>\mathrm{D}\!</math> at once overwhelms its discrete and finite powers to grasp them. But here, in the fully serene idylls of [[zeroth order logic]], we find ourselves fit with the compass of a wit that is all we'd ever need to explore their effects with care. | ||
| + | |||
| + | So let us do just that. | ||
| + | |||
| + | I will first rationalize the novel grouping of propositional forms in the last set of Tables, as that will extend a gentle invitation to the mathematical subject of ''group theory'', and demonstrate its relevance to differential logic in a strikingly apt and useful way. The data for that account is contained in Table A3. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Table A3.}~~\mathrm{E}f ~\text{Expanded over Differential Features}~ \{ \mathrm{d}p, \mathrm{d}q \}\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | width="10%" | | ||
| + | | width="18%" | <math>f\!</math> | ||
| + | | width="18%" | | ||
| + | <p><math>\mathrm{T}_{11} f\!</math></p> | ||
| + | <p><math>\mathrm{E}f|_{\mathrm{d}p~\mathrm{d}q}\!</math></p> | ||
| + | | width="18%" | | ||
| + | <p><math>\mathrm{T}_{10} f\!</math></p> | ||
| + | <p><math>\mathrm{E}f|_{\mathrm{d}p(\mathrm{d}q)}\!</math></p> | ||
| + | | width="18%" | | ||
| + | <p><math>\mathrm{T}_{01} f\!</math></p> | ||
| + | <p><math>\mathrm{E}f|_{(\mathrm{d}p)\mathrm{d}q}\!</math></p> | ||
| + | | width="18%" | | ||
| + | <p><math>\mathrm{T}_{00} f\!</math></p> | ||
| + | <p><math>\mathrm{E}f|_{(\mathrm{d}p)(\mathrm{d}q)}\!</math></p> | ||
| + | |- | ||
| + | | <math>f_0\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | | <math>(~)\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_1 | ||
| + | \\[4pt] | ||
| + | f_2 | ||
| + | \\[4pt] | ||
| + | f_4 | ||
| + | \\[4pt] | ||
| + | f_8 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~p~~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | (p)(q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \\[4pt] | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p)(q) | ||
| + | \\[4pt] | ||
| + | (p)~q~ | ||
| + | \\[4pt] | ||
| + | ~p~(q) | ||
| + | \\[4pt] | ||
| + | ~p~~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_3 | ||
| + | \\[4pt] | ||
| + | f_{12} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~p~ | ||
| + | \\[4pt] | ||
| + | (p) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~p~ | ||
| + | \\[4pt] | ||
| + | (p) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (p) | ||
| + | \\[4pt] | ||
| + | ~p~ | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_6 | ||
| + | \\[4pt] | ||
| + | f_9 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((p,~q)) | ||
| + | \\[4pt] | ||
| + | ~(p,~q)~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((p,~q)) | ||
| + | \\[4pt] | ||
| + | ~(p,~q)~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~(p,~q)~ | ||
| + | \\[4pt] | ||
| + | ((p,~q)) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_5 | ||
| + | \\[4pt] | ||
| + | f_{10} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~q~ | ||
| + | \\[4pt] | ||
| + | (q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ~q~ | ||
| + | \\[4pt] | ||
| + | (q) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (q) | ||
| + | \\[4pt] | ||
| + | ~q~ | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | f_7 | ||
| + | \\[4pt] | ||
| + | f_{11} | ||
| + | \\[4pt] | ||
| + | f_{13} | ||
| + | \\[4pt] | ||
| + | f_{14} | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~p~~q~) | ||
| + | \\[4pt] | ||
| + | (~p~(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q~) | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((p)(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q~) | ||
| + | \\[4pt] | ||
| + | (~p~(q)) | ||
| + | \\[4pt] | ||
| + | (~p~~q~) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ((p)~q~) | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \\[4pt] | ||
| + | (~p~~q~) | ||
| + | \\[4pt] | ||
| + | (~p~(q)) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~p~(q)) | ||
| + | \\[4pt] | ||
| + | (~p~~q~) | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q~) | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (~p~~q~) | ||
| + | \\[4pt] | ||
| + | (~p~(q)) | ||
| + | \\[4pt] | ||
| + | ((p)~q~) | ||
| + | \\[4pt] | ||
| + | ((p)(q)) | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | <math>f_{15}\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | | <math>((~))\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | colspan="2" | <math>\text{Fixed Point Total}\!</math> | ||
| + | | <math>4\!</math> | ||
| + | | <math>4\!</math> | ||
| + | | <math>4\!</math> | ||
| + | | <math>16\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | The shift operator <math>\mathrm{E}\!</math> can be understood as enacting a substitution operation on the propositional form <math>f(p, q)\!</math> that is given as its argument. In our present focus on propositional forms that involve two variables, we have the following type specifications and definitions: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | | ||
| + | <math>\begin{array}{lcl} | ||
| + | \mathrm{E} ~:~ (X \to \mathbb{B}) | ||
| + | & \to & | ||
| + | (\mathrm{E}X \to \mathbb{B}) | ||
| + | \\[6pt] | ||
| + | \mathrm{E} ~:~ f(p, q) | ||
| + | & \mapsto & | ||
| + | \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) | ||
| + | \\[6pt] | ||
| + | \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) | ||
| + | & = & | ||
| + | f(p + \mathrm{d}p, q + \mathrm{d}q) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | f( \texttt{(} p, \mathrm{d}p \texttt{)}, \texttt{(} q, \mathrm{d}q \texttt{)} ) | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | Evaluating <math>\mathrm{E}f\!</math> at particular values of <math>\mathrm{d}p\!</math> and <math>\mathrm{d}q,\!</math> for example, <math>\mathrm{d}p = i\!</math> and <math>\mathrm{d}q = j,\!</math> where <math>i\!</math> and <math>j\!</math> are values in <math>\mathbb{B},\!</math> produces the following result: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | | ||
| + | <math>\begin{array}{lclcl} | ||
| + | \mathrm{E}_{ij} | ||
| + | & : & | ||
| + | (X \to \mathbb{B}) | ||
| + | & \to & | ||
| + | (X \to \mathbb{B}) | ||
| + | \\[6pt] | ||
| + | \mathrm{E}_{ij} | ||
| + | & : & | ||
| + | f | ||
| + | & \mapsto & | ||
| + | \mathrm{E}_{ij}f | ||
| + | \\[6pt] | ||
| + | \mathrm{E}_{ij}f | ||
| + | & = & | ||
| + | \mathrm{E}f|_{\mathrm{d}p = i, \mathrm{d}q = j} | ||
| + | & = & | ||
| + | f(p + i, q + j) | ||
| + | \\[6pt] | ||
| + | & & | ||
| + | & = & | ||
| + | f( \texttt{(} p, i \texttt{)}, \texttt{(} q, j \texttt{)} ) | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | The notation is a little awkward, but the data of Table A3 should make the sense clear. The important thing to observe is that <math>\mathrm{E}_{ij}\!</math> has the effect of transforming each proposition <math>f : X \to \mathbb{B}\!</math> into a proposition <math>f^\prime : X \to \mathbb{B}.\!</math> As it happens, the action of each <math>\mathrm{E}_{ij}\!</math> is one-to-one and onto, so the gang of four operators <math>\{ \mathrm{E}_{ij} : i, j \in \mathbb{B} \}\!</math> is an example of what is called a ''transformation group'' on the set of sixteen propositions. Bowing to a longstanding local and linear tradition, I will therefore redub the four elements of this group as <math>\mathrm{T}_{00}, \mathrm{T}_{01}, \mathrm{T}_{10}, \mathrm{T}_{11},\!</math> to bear in mind their transformative character, or nature, as the case may be. Abstractly viewed, this group of order four has the following operation table: | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center; width:60%" | ||
| + | |- style="height:50px" | ||
| + | | width="12%" style="border-bottom:1px solid black; border-right:1px solid black" | | ||
| + | <math>\cdot\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{T}_{00}\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{T}_{01}\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{T}_{10}\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{T}_{11}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{T}_{00}\!</math> | ||
| + | | <math>\mathrm{T}_{00}\!</math> | ||
| + | | <math>\mathrm{T}_{01}\!</math> | ||
| + | | <math>\mathrm{T}_{10}\!</math> | ||
| + | | <math>\mathrm{T}_{11}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{T}_{01}\!</math> | ||
| + | | <math>\mathrm{T}_{01}\!</math> | ||
| + | | <math>\mathrm{T}_{00}\!</math> | ||
| + | | <math>\mathrm{T}_{11}\!</math> | ||
| + | | <math>\mathrm{T}_{10}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{T}_{10}\!</math> | ||
| + | | <math>\mathrm{T}_{10}\!</math> | ||
| + | | <math>\mathrm{T}_{11}\!</math> | ||
| + | | <math>\mathrm{T}_{00}\!</math> | ||
| + | | <math>\mathrm{T}_{01}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{T}_{11}\!</math> | ||
| + | | <math>\mathrm{T}_{11}\!</math> | ||
| + | | <math>\mathrm{T}_{10}\!</math> | ||
| + | | <math>\mathrm{T}_{01}\!</math> | ||
| + | | <math>\mathrm{T}_{00}\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | It happens that there are just two possible groups of 4 elements. One is the cyclic group <math>Z_4\!</math> (from German ''Zyklus''), which this is not. The other is the Klein four-group <math>V_4\!</math> (from German ''Vier''), which this is. | ||
| + | |||
| + | More concretely viewed, the group as a whole pushes the set of sixteen propositions around in such a way that they fall into seven natural classes, called ''orbits''. One says that the orbits are preserved by the action of the group. There is an ''Orbit Lemma'' of immense utility to “those who count” which, depending on your upbringing, you may associate with the names of Burnside, Cauchy, Frobenius, or some subset or superset of these three, vouching that the number of orbits is equal to the mean number of fixed points, in other words, the total number of points (in our case, propositions) that are left unmoved by the separate operations, divided by the order of the group. In this instance, <math>\mathrm{T}_{00}\!</math> operates as the group identity, fixing all 16 propositions, while the other three group elements fix 4 propositions each, and so we get: Number of Orbits = (4 + 4 + 4 + 16) ÷ 4 = 7. Amazing! | ||
| + | |||
| + | {| align="center" cellpadding="0" cellspacing="0" width="90%" | ||
| + | | | ||
| + | <p>Consider what effects that might ''conceivably'' have practical bearings you ''conceive'' the objects of your ''conception'' to have. Then, your ''conception'' of those effects is the whole of your ''conception'' of the object.</p> | ||
| + | |- | ||
| + | | align="right" | — Charles Sanders Peirce, “Issues of Pragmaticism”, (CP 5.438) | ||
| + | |} | ||
| + | |||
| + | One other subject that it would be opportune to mention at this point, while we have an object example of a mathematical group fresh in mind, is the relationship between the pragmatic maxim and what are commonly known in mathematics as ''representation principles''. As it turns out, with regard to its formal characteristics, the pragmatic maxim unites the aspects of a representation principle with the attributes of what would ordinarily be known as a ''closure principle''. We will consider the form of closure that is invoked by the pragmatic maxim on another occasion, focusing here and now on the topic of group representations. | ||
| + | |||
| + | Let us return to the example of the ''four-group'' <math>V_4.\!</math> We encountered this group in one of its concrete representations, namely, as a ''transformation group'' that acts on a set of objects, in this case a set of sixteen functions or propositions. Forgetting about the set of objects that the group transforms among themselves, we may take the abstract view of the group's operational structure, for example, in the form of the group operation table copied here: | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center; width:60%" | ||
| + | |- style="height:50px" | ||
| + | | width="12%" style="border-bottom:1px solid black; border-right:1px solid black" | | ||
| + | <math>\cdot\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{e}\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{f}\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{g}\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{h}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{e}\!</math> | ||
| + | | <math>\mathrm{e}\!</math> | ||
| + | | <math>\mathrm{f}\!</math> | ||
| + | | <math>\mathrm{g}\!</math> | ||
| + | | <math>\mathrm{h}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{f}\!</math> | ||
| + | | <math>\mathrm{f}\!</math> | ||
| + | | <math>\mathrm{e}\!</math> | ||
| + | | <math>\mathrm{h}\!</math> | ||
| + | | <math>\mathrm{g}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{g}\!</math> | ||
| + | | <math>\mathrm{g}\!</math> | ||
| + | | <math>\mathrm{h}\!</math> | ||
| + | | <math>\mathrm{e}\!</math> | ||
| + | | <math>\mathrm{f}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{h}\!</math> | ||
| + | | <math>\mathrm{h}\!</math> | ||
| + | | <math>\mathrm{g}\!</math> | ||
| + | | <math>\mathrm{f}\!</math> | ||
| + | | <math>\mathrm{e}\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | This table is abstractly the same as, or isomorphic to, the versions with the <math>\mathrm{E}_{ij}\!</math> operators and the <math>\mathrm{T}_{ij}\!</math> transformations that we took up earlier. That is to say, the story is the same, only the names have been changed. An abstract group can have a variety of significantly and superficially different representations. But even after we have long forgotten the details of any particular representation there is a type of concrete representations, called ''regular representations'', that are always readily available, as they can be generated from the mere data of the abstract operation table itself. | ||
| + | |||
| + | To see how a regular representation is constructed from the abstract operation table, select a group element from the top margin of the Table, and “consider its effects” on each of the group elements as they are listed along the left margin. We may record these effects as Peirce usually did, as a ''logical aggregate'' of elementary dyadic relatives, that is, as a logical disjunction or boolean sum whose terms represent the ordered pairs of <math>\mathrm{input} : \mathrm{output}\!</math> transactions that are produced by each group element in turn. This forms one of the two possible ''regular representations'' of the group, in this case the one that is called the ''post-regular representation'' or the ''right regular representation''. It has long been conventional to organize the terms of this logical aggregate in the form of a matrix: | ||
| + | |||
| + | Reading “<math>+\!</math>” as a logical disjunction: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{G} | ||
| + | & = & \mathrm{e} | ||
| + | & + & \mathrm{f} | ||
| + | & + & \mathrm{g} | ||
| + | & + & \mathrm{h} | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | And so, by expanding effects, we get: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{G} | ||
| + | & = & \mathrm{e}:\mathrm{e} | ||
| + | & + & \mathrm{f}:\mathrm{f} | ||
| + | & + & \mathrm{g}:\mathrm{g} | ||
| + | & + & \mathrm{h}:\mathrm{h} | ||
| + | \\[4pt] | ||
| + | & + & \mathrm{e}:\mathrm{f} | ||
| + | & + & \mathrm{f}:\mathrm{e} | ||
| + | & + & \mathrm{g}:\mathrm{h} | ||
| + | & + & \mathrm{h}:\mathrm{g} | ||
| + | \\[4pt] | ||
| + | & + & \mathrm{e}:\mathrm{g} | ||
| + | & + & \mathrm{f}:\mathrm{h} | ||
| + | & + & \mathrm{g}:\mathrm{e} | ||
| + | & + & \mathrm{h}:\mathrm{f} | ||
| + | \\[4pt] | ||
| + | & + & \mathrm{e}:\mathrm{h} | ||
| + | & + & \mathrm{f}:\mathrm{g} | ||
| + | & + & \mathrm{g}:\mathrm{f} | ||
| + | & + & \mathrm{h}:\mathrm{e} | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | More on the pragmatic maxim as a representation principle later. | ||
| + | |||
| + | The above-mentioned fact about the regular representations of a group is universally known as Cayley's Theorem, typically stated in the following form: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | Every group is isomorphic to a subgroup of <math>\mathrm{Aut}(X),\!</math> the group of automorphisms of a suitably chosen set <math>X\!</math>. | ||
| + | |} | ||
| + | |||
| + | There is a considerable generalization of these regular representations to a broad class of relational algebraic systems in Peirce's earliest papers. The crux of the whole idea is this: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | Contemplate the effects of the symbol whose meaning you wish to investigate as they play out on all the stages of conduct where you can imagine that symbol playing a role. | ||
| + | |} | ||
| + | |||
| + | This idea of contextual definition by way of conduct transforming operators is basically the same as Jeremy Bentham's notion of ''paraphrasis'', a “method of accounting for fictions by explaining various purported terms away” (Quine, in Van Heijenoort, ''From Frege to Gödel'', p. 216). Today we'd call these constructions ''term models''. This, again, is the big idea behind Schönfinkel's combinators <math>\mathrm{S}, \mathrm{K}, \mathrm{I},\!</math> and hence of lambda calculus, and I reckon you know where that leads. | ||
| + | |||
| + | The next few excursions in this series will provide a scenic tour of various ideas in group theory that will turn out to be of constant guidance in several of the settings that are associated with our topic. | ||
| + | |||
| + | Let me return to Peirce's early papers on the algebra of relatives to pick up the conventions that he used there, and then rewrite my account of regular representations in a way that conforms to those. | ||
| + | |||
| + | Peirce describes the action of an “elementary dual relative” in this way: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | Elementary simple relatives are connected together in systems of four. For if <math>\mathrm{A}\!:\!\mathrm{B}\!</math> be taken to denote the elementary relative which multiplied into <math>\mathrm{B}\!</math> gives <math>\mathrm{A},\!</math> then this relation existing as elementary, we have the four elementary relatives | ||
| + | |- | ||
| + | | align="center" | <math>\mathrm{A}\!:\!\mathrm{A} \qquad \mathrm{A}\!:\!\mathrm{B} \qquad \mathrm{B}\!:\!\mathrm{A} \qquad \mathrm{B}\!:\!\mathrm{B}.\!</math> | ||
| + | |- | ||
| + | | C.S. Peirce, ''Collected Papers'', CP 3.123. | ||
| + | |} | ||
| + | |||
| + | Peirce is well aware that it is not at all necessary to arrange the elementary relatives of a relation into arrays, matrices, or tables, but when he does so he tends to prefer organizing 2-adic relations in the following manner: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{bmatrix} | ||
| + | a\!:\!a & a\!:\!b & a\!:\!c | ||
| + | \\ | ||
| + | b\!:\!a & b\!:\!b & b\!:\!c | ||
| + | \\ | ||
| + | c\!:\!a & c\!:\!b & c\!:\!c | ||
| + | \end{bmatrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | For example, given the set <math>X = \{ a, b, c \},\!</math> suppose that we have the 2-adic relative term <math>\mathit{m} = {}^{\backprime\backprime}\, \text{marker for}\, \underline{~ ~ ~}\, {}^{\prime\prime}~\!</math> and the associated 2-adic relation <math>M \subseteq X \times X,\!</math> the general pattern of whose common structure is represented by the following matrix: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math> | ||
| + | M \quad = \quad | ||
| + | \begin{bmatrix} | ||
| + | M_{aa}(a\!:\!a) & M_{ab}(a\!:\!b) & M_{ac}(a\!:\!c) | ||
| + | \\ | ||
| + | M_{ba}(b\!:\!a) & M_{bb}(b\!:\!b) & M_{bc}(b\!:\!c) | ||
| + | \\ | ||
| + | M_{ca}(c\!:\!a) & M_{cb}(c\!:\!b) & M_{cc}(c\!:\!c) | ||
| + | \end{bmatrix} | ||
| + | \!</math> | ||
| + | |} | ||
| + | |||
| + | For at least a little while longer, I will keep explicit the distinction between a ''relative term'' like <math>\mathit{m}\!</math> and a ''relation'' like <math>M \subseteq X \times X,\!</math> but it is best to view both these entities as involving different applications of the same information, and so we could just as easily write the following form: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math> | ||
| + | m \quad = \quad | ||
| + | \begin{bmatrix} | ||
| + | m_{aa}(a\!:\!a) & m_{ab}(a\!:\!b) & m_{ac}(a\!:\!c) | ||
| + | \\ | ||
| + | m_{ba}(b\!:\!a) & m_{bb}(b\!:\!b) & m_{bc}(b\!:\!c) | ||
| + | \\ | ||
| + | m_{ca}(c\!:\!a) & m_{cb}(c\!:\!b) & m_{cc}(c\!:\!c) | ||
| + | \end{bmatrix} | ||
| + | \!</math> | ||
| + | |} | ||
| + | |||
| + | By way of making up a concrete example, let us say that <math>\mathit{m}\!</math> or <math>M\!</math> is given as follows: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{array}{l} | ||
| + | a ~\text{is a marker for}~ a | ||
| + | \\ | ||
| + | a ~\text{is a marker for}~ b | ||
| + | \\ | ||
| + | b ~\text{is a marker for}~ b | ||
| + | \\ | ||
| + | b ~\text{is a marker for}~ c | ||
| + | \\ | ||
| + | c ~\text{is a marker for}~ c | ||
| + | \\ | ||
| + | c ~\text{is a marker for}~ a | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | In sum, then, the relative term <math>\mathit{m}\!</math> and the relation <math>M\!</math> are both represented by the following matrix: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{bmatrix} | ||
| + | 1 \cdot (a\!:\!a) & 1 \cdot (a\!:\!b) & 0 \cdot (a\!:\!c) | ||
| + | \\ | ||
| + | 0 \cdot (b\!:\!a) & 1 \cdot (b\!:\!b) & 1 \cdot (b\!:\!c) | ||
| + | \\ | ||
| + | 1 \cdot (c\!:\!a) & 0 \cdot (c\!:\!b) & 1 \cdot (c\!:\!c) | ||
| + | \end{bmatrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | I think this much will serve to fix notation and set up the remainder of the discussion. | ||
| + | |||
| + | In Peirce's time, and even in some circles of mathematics today, the information indicated by the elementary relatives <math>(i\!:\!j),\!</math> as the indices <math>i, j\!</math> range over the universe of discourse, would be referred to as the ''umbral elements'' of the algebraic operation represented by the matrix, though I seem to recall that Peirce preferred to call these terms the “ingredients”. When this ordered basis is understood well enough, one will tend to drop any mention of it from the matrix itself, leaving us nothing but these bare bones: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math> | ||
| + | M \quad = \quad | ||
| + | \begin{bmatrix} | ||
| + | 1 & 1 & 0 | ||
| + | \\ | ||
| + | 0 & 1 & 1 | ||
| + | \\ | ||
| + | 1 & 0 & 1 | ||
| + | \end{bmatrix} | ||
| + | \!</math> | ||
| + | |} | ||
| + | |||
| + | The various representations of <math>M\!</math> are nothing more than alternative ways of specifying its basic ingredients, namely, the following aggregate of elementary relatives: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{array}{*{13}{c}} | ||
| + | M | ||
| + | & = & a\!:\!a | ||
| + | & + & b\!:\!b | ||
| + | & + & c\!:\!c | ||
| + | & + & a\!:\!b | ||
| + | & + & b\!:\!c | ||
| + | & + & c\!:\!a | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | Recognizing that <math>a\!:\!a + b\!:\!b + c\!:\!c\!</math> is the identity transformation otherwise known as <math>\mathit{1},\!</math> the 2-adic relative term <math>m = {}^{\backprime\backprime}\, \text{marker for}\, \underline{~ ~ ~}\, {}^{\prime\prime}~\!</math> can be parsed as an element <math>\mathit{1} + a\!:\!b + b\!:\!c + c\!:\!a\!</math> of the so-called ''group ring'', all of which makes this element just a special sort of linear transformation. | ||
| + | |||
| + | Up to this point, we are still reading the elementary relatives of the form <math>i\!:\!j\!</math> in the way that Peirce read them in logical contexts: <math>i\!</math> is the relate, <math>j\!</math> is the correlate, and in our current example <math>i\!:\!j,\!</math> or more exactly, <math>m_{ij} = 1,\!</math> is taken to say that <math>i\!</math> is a marker for <math>j.\!</math> This is the mode of reading that we call “multiplying on the left”. | ||
| + | |||
| + | In the algebraic, permutational, or transformational contexts of application, however, Peirce converts to the alternative mode of reading, although still calling <math>i\!</math> the relate and <math>j\!</math> the correlate, the elementary relative <math>i\!:\!j\!</math> now means that <math>i\!</math> gets changed into <math>j.\!</math> In this scheme of reading, the transformation <math>a\!:\!b + b\!:\!c + c\!:\!a\!</math> is a permutation of the aggregate <math>\mathbf{1} = a + b + c,\!</math> or what we would now call the set <math>\{ a, b, c \},\!</math> in particular, it is the permutation that is otherwise notated as follows: | ||
| + | |||
| + | {| align="center" cellpadding="6" | ||
| + | | | ||
| + | <math>\begin{Bmatrix} | ||
| + | a & b & c | ||
| + | \\ | ||
| + | b & c & a | ||
| + | \end{Bmatrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | This is consistent with the convention that Peirce uses in the paper “On a Class of Multiple Algebras” (CP 3.324–327). | ||
| + | |||
| + | We've been exploring the applications of a certain technique for clarifying abstruse concepts, a rough-cut version of the pragmatic maxim that I've been accustomed to refer to as the ''operationalization'' of ideas. The basic idea is to replace the question of ''What it is'', which modest people comprehend is far beyond their powers to answer definitively any time soon, with the question of ''What it does'', which most people know at least a modicum about. | ||
| + | |||
| + | In the case of regular representations of groups we found a non-plussing surplus of answers to sort our way through. So let us track back one more time to see if we can learn any lessons that might carry over to more realistic cases. | ||
| + | |||
| + | Here is is the operation table of <math>V_4\!</math> once again: | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center; width:60%" | ||
| + | |+ <math>\text{Klein Four-Group}~ V_4\!</math> | ||
| + | |- style="height:50px" | ||
| + | | width="12%" style="border-bottom:1px solid black; border-right:1px solid black" | | ||
| + | <math>\cdot\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{e}\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{f}\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{g}\!</math> | ||
| + | | width="22%" style="border-bottom:1px solid black" | | ||
| + | <math>\mathrm{h}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{e}\!</math> | ||
| + | | <math>\mathrm{e}\!</math> | ||
| + | | <math>\mathrm{f}\!</math> | ||
| + | | <math>\mathrm{g}\!</math> | ||
| + | | <math>\mathrm{h}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{f}\!</math> | ||
| + | | <math>\mathrm{f}\!</math> | ||
| + | | <math>\mathrm{e}\!</math> | ||
| + | | <math>\mathrm{h}\!</math> | ||
| + | | <math>\mathrm{g}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{g}\!</math> | ||
| + | | <math>\mathrm{g}\!</math> | ||
| + | | <math>\mathrm{h}\!</math> | ||
| + | | <math>\mathrm{e}\!</math> | ||
| + | | <math>\mathrm{f}\!</math> | ||
| + | |- style="height:50px" | ||
| + | | style="border-right:1px solid black" | <math>\mathrm{h}\!</math> | ||
| + | | <math>\mathrm{h}\!</math> | ||
| + | | <math>\mathrm{g}\!</math> | ||
| + | | <math>\mathrm{f}\!</math> | ||
| + | | <math>\mathrm{e}\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | A group operation table is really just a device for recording a certain 3-adic relation, to be specific, the set of triples of the form <math>(x, y, z)\!</math> satisfying the equation <math>x \cdot y = z.\!</math> | ||
| + | |||
| + | In the case of <math>V_4 = (G, \cdot),\!</math> where <math>G\!</math> is the ''underlying set'' <math>\{ \mathrm{e}, \mathrm{f}, \mathrm{g}, \mathrm{h} \},\!</math> we have the 3-adic relation <math>L(V_4) \subseteq G \times G \times G\!</math> whose triples are listed below: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{matrix} | ||
| + | (\mathrm{e}, \mathrm{e}, \mathrm{e}) & | ||
| + | (\mathrm{e}, \mathrm{f}, \mathrm{f}) & | ||
| + | (\mathrm{e}, \mathrm{g}, \mathrm{g}) & | ||
| + | (\mathrm{e}, \mathrm{h}, \mathrm{h}) | ||
| + | \\[6pt] | ||
| + | (\mathrm{f}, \mathrm{e}, \mathrm{f}) & | ||
| + | (\mathrm{f}, \mathrm{f}, \mathrm{e}) & | ||
| + | (\mathrm{f}, \mathrm{g}, \mathrm{h}) & | ||
| + | (\mathrm{f}, \mathrm{h}, \mathrm{g}) | ||
| + | \\[6pt] | ||
| + | (\mathrm{g}, \mathrm{e}, \mathrm{g}) & | ||
| + | (\mathrm{g}, \mathrm{f}, \mathrm{h}) & | ||
| + | (\mathrm{g}, \mathrm{g}, \mathrm{e}) & | ||
| + | (\mathrm{g}, \mathrm{h}, \mathrm{f}) | ||
| + | \\[6pt] | ||
| + | (\mathrm{h}, \mathrm{e}, \mathrm{h}) & | ||
| + | (\mathrm{h}, \mathrm{f}, \mathrm{g}) & | ||
| + | (\mathrm{h}, \mathrm{g}, \mathrm{f}) & | ||
| + | (\mathrm{h}, \mathrm{h}, \mathrm{e}) | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | It is part of the definition of a group that the 3-adic relation <math>L \subseteq G^3\!</math> is actually a function <math>L : G \times G \to G.\!</math> It is from this functional perspective that we can see an easy way to derive the two regular representations. Since we have a function of the type <math>L : G \times G \to G,\!</math> we can define a couple of substitution operators: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | valign="top" | 1. | ||
| + | | <math>\mathrm{Sub}(x, (\underline{~~}, y))\!</math> puts any specified <math>x\!</math> into the empty slot of the rheme <math>(\underline{~~}, y),\!</math> with the effect of producing the saturated rheme <math>(x, y)\!</math> that evaluates to <math>xy.~\!</math> | ||
| + | |- | ||
| + | | valign="top" | 2. | ||
| + | | <math>\mathrm{Sub}(x, (y, \underline{~~}))\!</math> puts any specified <math>x\!</math> into the empty slot of the rheme <math>(y, \underline{~~}),\!</math> with the effect of producing the saturated rheme <math>(y, x)\!</math> that evaluates to <math>yx.~\!</math> | ||
| + | |} | ||
| + | |||
| + | In (1) we consider the effects of each <math>x\!</math> in its practical bearing on contexts of the form <math>(\underline{~~}, y),\!</math> as <math>y\!</math> ranges over <math>G,\!</math> and the effects are such that <math>x\!</math> takes <math>(\underline{~~}, y)\!</math> into <math>xy,\!</math> for <math>y\!</math> in <math>G,\!</math> all of which is notated as <math>x = \{ (y : xy) ~|~ y \in G \}.\!</math> The pairs <math>(y : xy)\!</math> can be found by picking an <math>x\!</math> from the left margin of the group operation table and considering its effects on each <math>y\!</math> in turn as these run across the top margin. This aspect of pragmatic definition we recognize as the regular ante-representation: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{e} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{h} | ||
| + | \\[4pt] | ||
| + | \mathrm{f} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{g} | ||
| + | \\[4pt] | ||
| + | \mathrm{g} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{f} | ||
| + | \\[4pt] | ||
| + | \mathrm{h} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{e} | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | In (2) we consider the effects of each <math>x\!</math> in its practical bearing on contexts of the form <math>(y, \underline{~~}),\!</math> as <math>y\!</math> ranges over <math>G,\!</math> and the effects are such that <math>x\!</math> takes <math>(y, \underline{~~})\!</math> into <math>yx,\!</math> for <math>y\!</math> in <math>G,\!</math> all of which is notated as <math>x = \{ (y : yx) ~|~ y \in G \}.\!</math> The pairs <math>(y : yx)\!</math> can be found by picking an <math>x\!</math> from the top margin of the group operation table and considering its effects on each <math>y\!</math> in turn as these run down the left margin. This aspect of pragmatic definition we recognize as the regular post-representation: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{e} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{h} | ||
| + | \\[4pt] | ||
| + | \mathrm{f} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{g} | ||
| + | \\[4pt] | ||
| + | \mathrm{g} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{f} | ||
| + | \\[4pt] | ||
| + | \mathrm{h} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{e} | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | If the ante-rep looks the same as the post-rep, now that I'm writing them in the same dialect, that is because <math>V_4\!</math> is abelian (commutative), and so the two representations have the very same effects on each point of their bearing. | ||
| + | |||
| + | So long as we're in the neighborhood, we might as well take in some more of the sights, for instance, the smallest example of a non-abelian (non-commutative) group. This is a group of six elements, say, <math>G = \{ \mathrm{e}, \mathrm{f}, \mathrm{g}, \mathrm{h}, \mathrm{i}, \mathrm{j} \},\!</math> with no relation to any other employment of these six symbols being implied, of course, and it can be most easily represented as the permutation group on a set of three letters, say, <math>X = \{ a, b, c \},\!</math> usually notated as <math>G = \mathrm{Sym}(X)\!</math> or more abstractly and briefly, as <math>\mathrm{Sym}(3)\!</math> or <math>S_3.\!</math> The next Table shows the intended correspondence between abstract group elements and the permutation or substitution operations in <math>\mathrm{Sym}(X).\!</math> | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Permutation Substitutions in}~ \mathrm{Sym} \{ a, b, c \}\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | width="16%" | <math>\mathrm{e}\!</math> | ||
| + | | width="16%" | <math>\mathrm{f}\!</math> | ||
| + | | width="16%" | <math>\mathrm{g}\!</math> | ||
| + | | width="16%" | <math>\mathrm{h}\!</math> | ||
| + | | width="16%" | <math>\mathrm{i}~\!</math> | ||
| + | | width="16%" | <math>\mathrm{j}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | a & b & c | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | c & a & b | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | b & c & a | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | a & c & b | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | c & b & a | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | b & a & c | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | Here is the operation table for <math>S_3,\!</math> given in abstract fashion: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | <math>\text{Symmetric Group}~ S_3\!</math> | ||
| + | |- | ||
| + | | [[Image:Symmetric Group S(3).jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | By the way, we will meet with the symmetric group <math>S_3~\!</math> again when we return to take up the study of Peirce's early paper “On a Class of Multiple Algebras” (CP 3.324–327), and also his late unpublished work “The Simplest Mathematics” (1902) (CP 4.227–323), with particular reference to the section that treats of “Trichotomic Mathematics” (CP 4.307–323). | ||
| + | |||
| + | By way of collecting a short-term pay-off for all the work that we did on the regular representations of the Klein 4-group <math>V_4,\!</math> let us write out as quickly as possible in ''relative form'' a minimal budget of representations for the symmetric group on three letters, <math>\mathrm{Sym}(3).\!</math> After doing the usual bit of compare and contrast among the various representations, we will have enough concrete material beneath our abstract belts to tackle a few of the presently obscured details of Peirce's early “Algebra + Logic” papers. | ||
| + | |||
| + | Writing the permutations or substitutions of <math>\mathrm{Sym} \{ a, b, c \}\!</math> in relative form generates what is generally thought of as a ''natural representation'' of <math>S_3.~\!</math> | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{e} | ||
| + | & = & a\!:\!a | ||
| + | & + & b\!:\!b | ||
| + | & + & c\!:\!c | ||
| + | \\[4pt] | ||
| + | \mathrm{f} | ||
| + | & = & a\!:\!c | ||
| + | & + & b\!:\!a | ||
| + | & + & c\!:\!b | ||
| + | \\[4pt] | ||
| + | \mathrm{g} | ||
| + | & = & a\!:\!b | ||
| + | & + & b\!:\!c | ||
| + | & + & c\!:\!a | ||
| + | \\[4pt] | ||
| + | \mathrm{h} | ||
| + | & = & a\!:\!a | ||
| + | & + & b\!:\!c | ||
| + | & + & c\!:\!b | ||
| + | \\[4pt] | ||
| + | \mathrm{i} | ||
| + | & = & a\!:\!c | ||
| + | & + & b\!:\!b | ||
| + | & + & c\!:\!a | ||
| + | \\[4pt] | ||
| + | \mathrm{j} | ||
| + | & = & a\!:\!b | ||
| + | & + & b\!:\!a | ||
| + | & + & c\!:\!c | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | I have without stopping to think about it written out this natural representation of <math>S_3~\!</math> in the style that comes most naturally to me, to wit, the “right” way, whereby an ordered pair configured as <math>x\!:\!y\!</math> constitutes the turning of <math>x\!</math> into <math>y.\!</math> It is possible that the next time we check in with CSP we will have to adjust our sense of direction, but that will be an easy enough bridge to cross when we come to it. | ||
| + | |||
| + | To construct the regular representations of <math>S_3,~\!</math> we begin with the data of its operation table: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | <math>\text{Symmetric Group}~ S_3\!</math> | ||
| + | |- | ||
| + | | [[Image:Symmetric Group S(3).jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | Just by way of staying clear about what we are doing, let's return to the recipe that we worked out before: | ||
| + | |||
| + | It is part of the definition of a group that the 3-adic relation <math>L \subseteq G^3\!</math> is actually a function <math>L : G \times G \to G.\!</math> It is from this functional perspective that we can see an easy way to derive the two regular representations. | ||
| + | |||
| + | Since we have a function of the type <math>L : G \times G \to G,\!</math> we can define a couple of substitution operators: | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | valign="top" | 1. | ||
| + | | <math>\mathrm{Sub}(x, (\underline{~~}, y))\!</math> puts any specified <math>x\!</math> into the empty slot of the rheme <math>(\underline{~~}, y),\!</math> with the effect of producing the saturated rheme <math>(x, y)\!</math> that evaluates to <math>xy.~\!</math> | ||
| + | |- | ||
| + | | valign="top" | 2. | ||
| + | | <math>\mathrm{Sub}(x, (y, \underline{~~}))\!</math> puts any specified <math>x\!</math> into the empty slot of the rheme <math>(y, \underline{~~}),\!</math> with the effect of producing the saturated rheme <math>(y, x)\!</math> that evaluates to <math>yx.~\!</math> | ||
| + | |} | ||
| + | |||
| + | In (1) we consider the effects of each <math>x\!</math> in its practical bearing on contexts of the form <math>(\underline{~~}, y),\!</math> as <math>y\!</math> ranges over <math>G,\!</math> and the effects are such that <math>x\!</math> takes <math>(\underline{~~}, y)\!</math> into <math>xy,\!</math> for <math>y\!</math> in <math>G,\!</math> all of which is notated as <math>x = \{ (y : xy) ~|~ y \in G \}.\!</math> The pairs <math>(y : xy)\!</math> can be found by picking an <math>x\!</math> from the left margin of the group operation table and considering its effects on each <math>y\!</math> in turn as these run along the right margin. This produces the ''regular ante-representation'' of <math>S_3,\!</math> like so: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | | ||
| + | <math>\begin{array}{*{13}{c}} | ||
| + | \mathrm{e} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{i} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{j} | ||
| + | \\[4pt] | ||
| + | \mathrm{f} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{j} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{i} | ||
| + | \\[4pt] | ||
| + | \mathrm{g} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{i} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{j} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{h} | ||
| + | \\[4pt] | ||
| + | \mathrm{h} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{i} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{j} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{g} | ||
| + | \\[4pt] | ||
| + | \mathrm{i} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{i} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{j} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{f} | ||
| + | \\[4pt] | ||
| + | \mathrm{j} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{j} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{i} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{e} | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | In (2) we consider the effects of each <math>x\!</math> in its practical bearing on contexts of the form <math>(y, \underline{~~}),\!</math> as <math>y\!</math> ranges over <math>G,\!</math> and the effects are such that <math>x\!</math> takes <math>(y, \underline{~~})\!</math> into <math>yx,\!</math> for <math>y\!</math> in <math>G,\!</math> all of which is notated as <math>x = \{ (y : yx) ~|~ y \in G \}.\!</math> The pairs <math>(y : yx)\!</math> can be found by picking an <math>x\!</math> on the right margin of the group operation table and considering its effects on each <math>y\!</math> in turn as these run along the left margin. This produces the ''regular post-representation'' of <math>S_3,\!</math> like so: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | | ||
| + | <math>\begin{array}{*{13}{c}} | ||
| + | \mathrm{e} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{i} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{j} | ||
| + | \\[4pt] | ||
| + | \mathrm{f} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{i} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{j} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{h} | ||
| + | \\[4pt] | ||
| + | \mathrm{g} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{j} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{i} | ||
| + | \\[4pt] | ||
| + | \mathrm{h} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{j} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{i} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{f} | ||
| + | \\[4pt] | ||
| + | \mathrm{i} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{i} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{j} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{e} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{g} | ||
| + | \\[4pt] | ||
| + | \mathrm{j} | ||
| + | & = & \mathrm{e}\!:\!\mathrm{j} | ||
| + | & + & \mathrm{f}\!:\!\mathrm{i} | ||
| + | & + & \mathrm{g}\!:\!\mathrm{h} | ||
| + | & + & \mathrm{h}\!:\!\mathrm{g} | ||
| + | & + & \mathrm{i}\!:\!\mathrm{f} | ||
| + | & + & \mathrm{j}\!:\!\mathrm{e} | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | If the ante-rep looks different from the post-rep, it is just as it should be, as <math>S_3~\!</math> is non-abelian (non-commutative), and so the two representations differ in the details of their practical effects, though, of course, being representations of the same abstract group, they must be isomorphic. | ||
| + | |||
| + | {| cellpadding="2" cellspacing="2" width="100%" | ||
| + | | width="60%" | | ||
| + | | width="40%" | | ||
| + | the way of heaven and earth<br> | ||
| + | is to be long continued<br> | ||
| + | in their operation<br> | ||
| + | without stopping | ||
| + | |- | ||
| + | | height="50px" | | ||
| + | | valign="top" | — i ching, hexagram 32 | ||
| + | |} | ||
| + | |||
| + | The Reader may be wondering what happened to the announced subject of ''Dynamics And Logic''. What happened was a bit like this: | ||
| + | |||
| + | We made the observation that the shift operators <math>\{ \mathrm{E}_{ij} \}\!</math> form a transformation group that acts on the set of propositions of the form <math>f : \mathbb{B} \times \mathbb{B} \to \mathbb{B}.\!</math> Group theory is a very attractive subject, but it did not draw us so far from our intended course as one might initially think. For one thing, groups, especially the groups that are named after the Norwegian mathematician [http://www-history.mcs.st-andrews.ac.uk/Biographies/Lie.html Marius Sophus Lie (1842–1899)], have turned out to be of critical utility in the solution of differential equations. For another thing, group operations provide us with an ample supply of triadic relations that have been extremely well-studied over the years, and thus they give us no small measure of useful guidance in the study of sign relations, another brand of 3-adic relations that have significance for logical studies, and in our acquaintance with which we have barely begun to break the ice. Finally, I couldn't resist taking up the links between group representations, amounting to the very archetypes of logical models, and the pragmatic maxim. | ||
| + | |||
| + | We've seen a couple of groups, <math>V_4\!</math> and <math>S_3,\!</math> represented in various ways, and we've seen their representations presented in a variety of different manners. Let us look at one other stylistic variant for presenting a representation that is frequently seen, the so-called ''matrix representation'' of a group. | ||
| + | |||
| + | Recalling the manner of our acquaintance with the symmetric group <math>S_3,\!</math> we began with the ''bigraph'' (bipartite graph) picture of its natural representation as the set of all permutations or substitutions on the set <math>X = \{ a, b, c \}.\!</math> | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Permutation Substitutions in}~ \mathrm{Sym} \{ a, b, c \}\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | width="16%" | <math>\mathrm{e}\!</math> | ||
| + | | width="16%" | <math>\mathrm{f}\!</math> | ||
| + | | width="16%" | <math>\mathrm{g}\!</math> | ||
| + | | width="16%" | <math>\mathrm{h}\!</math> | ||
| + | | width="16%" | <math>\mathrm{i}~\!</math> | ||
| + | | width="16%" | <math>\mathrm{j}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | a & b & c | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | c & a & b | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | b & c & a | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | a & c & b | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | c & b & a | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | a & b & c | ||
| + | \\[3pt] | ||
| + | \downarrow & \downarrow & \downarrow | ||
| + | \\[6pt] | ||
| + | b & a & c | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | These permutations were then converted to relative form as logical sums of elementary relatives: | ||
| + | |||
| + | {| align="center" cellpadding="10" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{e} | ||
| + | & = & a\!:\!a | ||
| + | & + & b\!:\!b | ||
| + | & + & c\!:\!c | ||
| + | \\[4pt] | ||
| + | \mathrm{f} | ||
| + | & = & a\!:\!c | ||
| + | & + & b\!:\!a | ||
| + | & + & c\!:\!b | ||
| + | \\[4pt] | ||
| + | \mathrm{g} | ||
| + | & = & a\!:\!b | ||
| + | & + & b\!:\!c | ||
| + | & + & c\!:\!a | ||
| + | \\[4pt] | ||
| + | \mathrm{h} | ||
| + | & = & a\!:\!a | ||
| + | & + & b\!:\!c | ||
| + | & + & c\!:\!b | ||
| + | \\[4pt] | ||
| + | \mathrm{i} | ||
| + | & = & a\!:\!c | ||
| + | & + & b\!:\!b | ||
| + | & + & c\!:\!a | ||
| + | \\[4pt] | ||
| + | \mathrm{j} | ||
| + | & = & a\!:\!b | ||
| + | & + & b\!:\!a | ||
| + | & + & c\!:\!c | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | From the relational representation of <math>\mathrm{Sym} \{ a, b, c \} \cong S_3,\!</math> one easily derives a ''linear representation'' of the group by viewing each permutation as a linear transformation that maps the elements of a suitable vector space onto each other. Each of these linear transformations is in turn represented by a 2-dimensional array of coefficients in <math>\mathbb{B},\!</math> resulting in the following set of matrices for the group: | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ <math>\text{Matrix Representations of Permutations in}~ \mathrm{Sym}(3)\!</math> | ||
| + | |- style="background:#f0f0ff" | ||
| + | | width="16%" | <math>\mathrm{e}\!</math> | ||
| + | | width="16%" | <math>\mathrm{f}\!</math> | ||
| + | | width="16%" | <math>\mathrm{g}\!</math> | ||
| + | | width="16%" | <math>\mathrm{h}\!</math> | ||
| + | | width="16%" | <math>\mathrm{i}~\!</math> | ||
| + | | width="16%" | <math>\mathrm{j}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 1 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 | ||
| + | \end{matrix}~\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0 & 0 & 1 | ||
| + | \\ | ||
| + | 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 1 & 0 | ||
| + | \end{matrix}~\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0 & 1 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 | ||
| + | \\ | ||
| + | 1 & 0 & 0 | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 1 & 0 | ||
| + | \end{matrix}~\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 1 & 0 | ||
| + | \\ | ||
| + | 1 & 0 & 0 | ||
| + | \end{matrix}~\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | 0 & 1 & 0 | ||
| + | \\ | ||
| + | 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 | ||
| + | \end{matrix}~\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | The key to the mysteries of these matrices is revealed by observing that their coefficient entries are arrayed and overlaid on a place-mat marked like so: | ||
| + | |||
| + | {| align="center" cellpadding="6" width="90%" | ||
| + | | align="center" | | ||
| + | <math>\begin{bmatrix} | ||
| + | a\!:\!a & | ||
| + | a\!:\!b & | ||
| + | a\!:\!c | ||
| + | \\ | ||
| + | b\!:\!a & | ||
| + | b\!:\!b & | ||
| + | b\!:\!c | ||
| + | \\ | ||
| + | c\!:\!a & | ||
| + | c\!:\!b & | ||
| + | c\!:\!c | ||
| + | \end{bmatrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | ==Quick Review : Field Picture== | ||
| + | |||
| + | Let us summarize, in rough but intuitive terms, the outlook on differential logic that we have reached so far. We've been considering a class of operators on universes of discourse, each of which takes us from considering one universe of discourse, <math>X^\circ,\!</math> to considering a larger universe of discourse, <math>\mathrm{E}X^\circ.\!</math> An operator <math>\mathrm{W}\!</math> of this general type, namely, <math>\mathrm{W} : X^\circ \to \mathrm{E}X^\circ,\!</math> acts on each proposition <math>f : X \to \mathbb{B}\!</math> of the source universe <math>{X^\circ}\!</math> to produce a proposition <math>\mathrm{W}f : \mathrm{E}X \to \mathbb{B}\!</math> of the target universe <math>\mathrm{E}X^\circ.\!</math> | ||
| + | |||
| + | The two main operators that we've examined so far are the enlargement or shift operator <math>\mathrm{E} : X^\circ \to \mathrm{E}X^\circ\!</math> and the difference operator <math>\mathrm{D} : X^\circ \to \mathrm{E}X^\circ.\!</math> The operators <math>\mathrm{E}\!</math> and <math>\mathrm{D}\!</math> act on propositions in <math>X^\circ,\!</math> that is, propositions of the form <math>f : X \to \mathbb{B}\!</math> that are said to be ''about'' the subject matter of <math>X,\!</math> and they produce extended propositions of the forms <math>\mathrm{E}f, \mathrm{D}f : \mathrm{E}X \to \mathbb{B},\!</math> propositions whose extended sets of variables allow them to be read as being about specified collections of changes that conceivably occur in <math>X.\!</math> | ||
| + | |||
| + | At this point we find ourselves in need of visual representations, suitable arrays of concrete pictures to anchor our more earthy intuitions and to help us keep our wits about us as we venture higher into the ever more rarefied air of abstractions. | ||
| + | |||
| + | One good picture comes to us by way of the ''field'' concept. Given a space <math>X,\!</math> a ''field'' of a specified type <math>Y\!</math> over <math>X\!</math> is formed by associating with each point of <math>X\!</math> an object of type <math>Y.\!</math> If that sounds like the same thing as a function from <math>X\!</math> to the space of things of type <math>Y\!</math> — it is nothing but — and yet it does seem helpful to vary the mental images and to take advantage of the figures of speech that spring to mind under the emblem of this field idea. | ||
| + | |||
| + | In the field picture a proposition <math>f : X \to \mathbb{B}\!</math> becomes a ''scalar field'', that is, a field of values in <math>\mathbb{B}.\!</math> | ||
| + | |||
| + | For example, consider the logical conjunction <math>pq : X \to \mathbb{B}\!</math> that is shown in the following venn diagram: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Field Picture PQ Conjunction.jpg|500px]] | ||
| + | |- | ||
| + | | <math>\text{Conjunction}~ pq : X \to \mathbb{B}\!</math> | ||
| + | |} | ||
| + | |||
| + | Each of the operators <math>\mathrm{E}, \mathrm{D} : X^\circ \to \mathrm{E}X^\circ\!</math> takes us from considering propositions <math>f : X \to \mathbb{B},\!</math> here viewed as ''scalar fields'' over <math>X,\!</math> to considering the corresponding ''differential fields'' over <math>X,\!</math> analogous to what are usually called ''vector fields'' over <math>X.\!</math> | ||
| + | |||
| + | The structure of these differential fields can be described this way. With each point of <math>X\!</math> there is associated an object of the following type: a proposition about changes in <math>X,\!</math> that is, a proposition <math>g : \mathrm{d}X \to \mathbb{B}.\!</math> In this frame of reference, if <math>{X^\circ}\!</math> is the universe that is generated by the set of coordinate propositions <math>\{ p, q \},\!</math> then <math>\mathrm{d}X^\circ\!</math> is the differential universe that is generated by the set of differential propositions <math>\{ \mathrm{d}p, \mathrm{d}q \}.\!</math> These differential propositions may be interpreted as indicating <math>{}^{\backprime\backprime} \text{change in}\, p \, {}^{\prime\prime}\!</math> and <math>{}^{\backprime\backprime} \text{change in}\, q \, {}^{\prime\prime},\!</math> respectively. | ||
| + | |||
| + | A differential operator <math>\mathrm{W},\!</math> of the first order class that we have been considering, takes a proposition <math>f : X \to \mathbb{B}\!</math> and gives back a differential proposition <math>\mathrm{W}f : \mathrm{E}X \to \mathbb{B}.\!</math> In the field view, we see the proposition <math>f : X \to \mathbb{B}\!</math> as a scalar field and we see the differential proposition <math>\mathrm{W}f : \mathrm{E}X \to \mathbb{B}\!</math> as a vector field, specifically, a field of propositions about contemplated changes in <math>X.\!</math> | ||
| + | |||
| + | The field of changes produced by <math>\mathrm{E}\!</math> on <math>pq\!</math> is shown in the next venn diagram: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Field Picture PQ Enlargement Conjunction.jpg|500px]] | ||
| + | |- | ||
| + | | <math>\text{Enlargement}~ \mathrm{E}(pq) : \mathrm{E}X \to \mathbb{B}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{array}{rcccccc} | ||
| + | \mathrm{E}(pq) | ||
| + | & = & | ||
| + | p | ||
| + | & \cdot & | ||
| + | q | ||
| + | & \cdot & | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | p | ||
| + | & \cdot & | ||
| + | \texttt{(} q \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} | ||
| + | & \cdot & | ||
| + | q | ||
| + | & \cdot & | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{(} q \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | The differential field <math>\mathrm{E}(pq)\!</math> specifies the changes that need to be made from each point of <math>X\!</math> in order to reach one of the models of the proposition <math>pq,\!</math> that is, in order to satisfy the proposition <math>pq.\!</math> | ||
| + | |||
| + | The field of changes produced by <math>\mathrm{D}\!</math> on <math>pq\!</math> is shown in the following venn diagram: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Field Picture PQ Difference Conjunction.jpg|500px]] | ||
| + | |- | ||
| + | | <math>\text{Difference}~ \mathrm{D}(pq) : \mathrm{E}X \to \mathbb{B}~\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{array}{rcccccc} | ||
| + | \mathrm{D}(pq) | ||
| + | & = & | ||
| + | p | ||
| + | & \cdot & | ||
| + | q | ||
| + | & \cdot & | ||
| + | \texttt{(} | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | \texttt{)} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | p | ||
| + | & \cdot & | ||
| + | \texttt{(} q \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{~} | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \texttt{~} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} | ||
| + | & \cdot & | ||
| + | q | ||
| + | & \cdot & | ||
| + | \texttt{~} | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | \texttt{~} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{(}q \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{~} | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \texttt{~} | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | The differential field <math>\mathrm{D}(pq)\!</math> specifies the changes that need to be made from each point of <math>X\!</math> in order to feel a change in the felt value of the field <math>pq.\!</math> | ||
| + | |||
| + | ===Proposition and Tacit Extension=== | ||
| + | |||
| + | Now that we've introduced the field picture as an aid to thinking about propositions and their analytic series, a very pleasing way of picturing the relationships among a proposition <math>f : X \to \mathbb{B},\!</math> its enlargement or shift map <math>\mathrm{E}f : \mathrm{E}X \to \mathbb{B},\!</math> and its difference map <math>\mathrm{D}f : \mathrm{E}X \to \mathbb{B}\!</math> can now be drawn. | ||
| + | |||
| + | To illustrate this possibility, let's return to the differential analysis of the conjunctive proposition <math>f(p, q) = pq,\!</math> giving the development a slightly different twist at the appropriate point. | ||
| + | |||
| + | The next venn diagram shows once again the proposition <math>pq,\!</math> which we now view as a scalar field — analogous to a ''potential hill'' in physics, but in logic tantamount to a ''potential plateau'' — where the shaded region indicates an elevation of 1 and the unshaded region indicates an elevation of 0. | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Field Picture PQ Conjunction.jpg|500px]] | ||
| + | |- | ||
| + | | <math>\text{Proposition}~ pq : X \to \mathbb{B}\!</math> | ||
| + | |} | ||
| + | |||
| + | Given a proposition <math>f : X \to \mathbb{B},\!</math> the ''tacit extension'' of <math>f\!</math> to <math>\mathrm{E}X\!</math> is denoted <math>\boldsymbol\varepsilon f : \mathrm{E}X \to \mathbb{B}~\!</math> and defined by the equation <math>\boldsymbol\varepsilon f = f,\!</math> so it's really just the same proposition residing in a bigger universe. Tacit extensions formalize the intuitive idea that a function on a particular set of variables can be extended to a function on a superset of those variables in such a way that the new function obeys the same constraints on the old variables, with a "don't care" condition on the new variables. | ||
| + | |||
| + | The tacit extension of the scalar field <math>pq : X \to \mathbb{B}\!</math> to the differential field <math>\boldsymbol\varepsilon (pq) : \mathrm{E}X \to \mathbb{B}\!</math> is shown in the following venn diagram: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Field Picture PQ Tacit Extension Conjunction.jpg|500px]] | ||
| + | |- | ||
| + | | <math>\text{Tacit Extension}~ \boldsymbol\varepsilon (pq) : \mathrm{E}X \to \mathbb{B}~\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{array}{rcccccc} | ||
| + | \boldsymbol\varepsilon (pq) | ||
| + | & = & | ||
| + | p & \cdot & q & \cdot & | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | p & \cdot & q & \cdot & | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | p & \cdot & q & \cdot & | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | p & \cdot & q & \cdot & | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | ===Enlargement and Difference Maps=== | ||
| + | |||
| + | Continuing with the example <math>pq : X \to \mathbb{B},\!</math> the next venn diagram shows the enlargement or shift map <math>\mathrm{E}(pq) : \mathrm{E}X \to \mathbb{B}\!</math> in the same style of differential field picture that we drew for the tacit extension <math>\boldsymbol\varepsilon (pq) : \mathrm{E}X \to \mathbb{B}.\!</math> | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Field Picture PQ Enlargement Conjunction.jpg|500px]] | ||
| + | |- | ||
| + | | <math>\text{Enlargement Map}~ \mathrm{E}(pq) : \mathrm{E}X \to \mathbb{B}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{array}{rcccccc} | ||
| + | \mathrm{E}(pq) | ||
| + | & = & | ||
| + | p | ||
| + | & \cdot & | ||
| + | q | ||
| + | & \cdot & | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | p | ||
| + | & \cdot & | ||
| + | \texttt{(} q \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} | ||
| + | & \cdot & | ||
| + | q | ||
| + | & \cdot & | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{(} q \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | A very important conceptual transition has just occurred here, almost tacitly, as it were. Generally speaking, having a set of mathematical objects of compatible types, in this case the two differential fields <math>\boldsymbol\varepsilon f\!</math> and <math>\mathrm{E}f,\!</math> both of the type <math>\mathrm{E}X \to \mathbb{B},\!</math> is very useful, because it allows us to consider these fields as integral mathematical objects that can be operated on and combined in the ways that we usually associate with algebras. | ||
| + | |||
| + | In this case one notices that the tacit extension <math>\boldsymbol\varepsilon f\!</math> and the enlargement <math>\mathrm{E}f\!</math> are in a certain sense dual to each other. The tacit extension <math>\boldsymbol\varepsilon f\!</math> indicates all the arrows out of the region where <math>f\!</math> is true and the enlargement <math>\mathrm{E}f\!</math> indicates all the arrows into the region where <math>f\!</math> is true. The only arc they have in common is the no-change loop <math>\texttt{(} \mathrm{d}p \texttt{)(} \mathrm{d}q \texttt{)}\!</math> at <math>pq.\!</math> If we add the two sets of arcs in mod 2 fashion then the loop of multiplicity 2 zeroes out, leaving the 6 arrows of <math>\mathrm{D}(pq) = \boldsymbol\varepsilon(pq) + \mathrm{E}(pq)\!</math> that are illustrated below: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Field Picture PQ Difference Conjunction.jpg|500px]] | ||
| + | |- | ||
| + | | <math>\text{Difference Map}~ \mathrm{D}(pq) : \mathrm{E}X \to \mathbb{B}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{array}{rcccccc} | ||
| + | \mathrm{D}(pq) | ||
| + | & = & | ||
| + | p | ||
| + | & \cdot & | ||
| + | q | ||
| + | & \cdot & | ||
| + | \texttt{(} | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | \texttt{)} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | p | ||
| + | & \cdot & | ||
| + | \texttt{(} q \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{~} | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \texttt{~} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} | ||
| + | & \cdot & | ||
| + | q | ||
| + | & \cdot & | ||
| + | \texttt{~} | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | \texttt{~} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{(}q \texttt{)} | ||
| + | & \cdot & | ||
| + | \texttt{~} | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \texttt{~} | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | ===Tangent and Remainder Maps=== | ||
| + | |||
| + | If we follow the classical line that singles out linear functions as ideals of simplicity, then we may complete the analytic series of the proposition <math>f = pq : X \to \mathbb{B}\!</math> in the following way. | ||
| + | |||
| + | The next venn diagram shows the differential proposition <math>\mathrm{d}f = \mathrm{d}(pq) : \mathrm{E}X \to \mathbb{B}\!</math> that we get by extracting the cell-wise linear approximation to the difference map <math>\mathrm{D}f = \mathrm{D}(pq) : \mathrm{E}X \to \mathbb{B}.\!</math> This is the logical analogue of what would ordinarily be called ''the'' differential of <math>pq,\!</math> but since I've been attaching the adjective ''differential'' to just about everything in sight, the distinction tends to be lost. For the time being, I'll resort to using the alternative name ''tangent map'' for <math>\mathrm{d}f.\!</math> | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Field Picture PQ Differential Conjunction.jpg|500px]] | ||
| + | |- | ||
| + | | <math>\text{Tangent Map}~ \mathrm{d}(pq) : \mathrm{E}X \to \mathbb{B}\!</math> | ||
| + | |} | ||
| + | |||
| + | Just to be clear about what's being indicated here, it's a visual way of summarizing the following data: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | | ||
| + | <math>\begin{array}{rcccccc} | ||
| + | \mathrm{d}(pq) | ||
| + | & = & | ||
| + | p & \cdot & q & \cdot & | ||
| + | \texttt{(} \mathrm{d}p \texttt{,} \mathrm{d}q \texttt{)} | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | p & \cdot & \texttt{(} q \texttt{)} & \cdot & | ||
| + | \mathrm{d}q | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} & \cdot & q & \cdot & | ||
| + | \mathrm{d}p | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & 0 | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | To understand the extended interpretations, that is, the conjunctions of basic and differential features that are being indicated here, it may help to note the following equivalences: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \texttt{(} | ||
| + | \mathrm{d}p | ||
| + | \texttt{,} | ||
| + | \mathrm{d}q | ||
| + | \texttt{)} | ||
| + | & = & | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | & + & | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \\[4pt] | ||
| + | dp | ||
| + | & = & | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | & + & | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{(} \mathrm{d}q \texttt{)} | ||
| + | \\[4pt] | ||
| + | \mathrm{d}q | ||
| + | & = & | ||
| + | \texttt{~} \mathrm{d}p \texttt{~} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | & + & | ||
| + | \texttt{(} \mathrm{d}p \texttt{)} | ||
| + | \texttt{~} \mathrm{d}q \texttt{~} | ||
| + | \end{matrix}\!</math> | ||
| + | |} | ||
| + | |||
| + | Capping the series that analyzes the proposition <math>pq\!</math> in terms of succeeding orders of linear propositions, the final venn diagram in this series shows the remainder map <math>\mathrm{r}(pq) : \mathrm{E}X \to \mathbb{B},\!</math> that happens to be linear in pairs of variables. | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | [[Image:Field Picture PQ Remainder Conjunction.jpg|500px]] | ||
| + | |- | ||
| + | | <math>\text{Remainder Map}~ \mathrm{r}(pq) : \mathrm{E}X \to \mathbb{B}\!</math> | ||
| + | |} | ||
| + | |||
| + | Reading the arrows off the map produces the following data: | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | | ||
| + | <math>\begin{array}{rcccccc} | ||
| + | \mathrm{r}(pq) | ||
| + | & = & | ||
| + | p & \cdot & q & \cdot & | ||
| + | \mathrm{d}p ~ \mathrm{d}q | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | p & \cdot & \texttt{(} q \texttt{)} & \cdot & | ||
| + | \mathrm{d}p ~ \mathrm{d}q | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} & \cdot & q & \cdot & | ||
| + | \mathrm{d}p ~ \mathrm{d}q | ||
| + | \\[4pt] | ||
| + | & + & | ||
| + | \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & | ||
| + | \mathrm{d}p ~ \mathrm{d}q | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | In short, <math>\mathrm{r}(pq)\!</math> is a constant field, having the value <math>\mathrm{d}p~\mathrm{d}q\!</math> at each cell. | ||
| + | |||
| + | ==Least Action Operators== | ||
| + | |||
| + | We have been contemplating functions of the type <math>f : X \to \mathbb{B}\!</math> and studying the action of the operators <math>\mathrm{E}\!</math> and <math>\mathrm{D}\!</math> on this family. These functions, that we may identify for our present aims with propositions, inasmuch as they capture their abstract forms, are logical analogues of ''scalar potential fields''. These are the sorts of fields that are so picturesquely presented in elementary calculus and physics textbooks by images of snow-covered hills and parties of skiers who trek down their slopes like least action heroes. The analogous scene in propositional logic presents us with forms more reminiscent of plateaunic idylls, being all plains at one of two levels, the mesas of verity and falsity, as it were, with nary a niche to inhabit between them, restricting our options for a sporting gradient of downhill dynamics to just one of two: standing still on level ground or falling off a bluff. | ||
| + | |||
| + | We are still working well within the logical analogue of the classical finite difference calculus, taking in the novelties that the logical transmutation of familiar elements is able to bring to light. Soon we will take up several different notions of approximation relationships that may be seen to organize the space of propositions, and these will allow us to define several different forms of differential analysis applying to propositions. In time we will find reason to consider more general types of maps, having concrete types of the form <math>X_1 \times \ldots \times X_k \to Y_1 \times \ldots \times Y_n\!</math> and abstract types <math>\mathbb{B}^k \to \mathbb{B}^n.\!</math> We will think of these mappings as transforming universes of discourse into themselves or into others, in short, as ''transformations of discourse''. | ||
| + | |||
| + | Before we continue with this intinerary, however, I would like to highlight another sort of differential aspect that concerns the ''boundary operator'' or the ''marked connective'' that serves as one of the two basic connectives in the cactus language for [[zeroth order logic]]. | ||
| + | |||
| + | For example, consider the proposition <math>f\!</math> of concrete type <math>f : P \times Q \times R \to \mathbb{B}\!</math> and abstract type <math>f : \mathbb{B}^3 \to \mathbb{B}\!</math> that is written <math>\texttt{(} p, q, r \texttt{)}\!</math> in cactus syntax. Taken as an assertion in what Peirce called the ''existential interpretation'', the proposition <math>\texttt{(} p, q, r \texttt{)}\!</math> says that just one of <math>p, q, r\!</math> is false. It is instructive to consider this assertion in relation to the logical conjunction <math>pqr\!</math> of the same propositions. A venn diagram of <math>\texttt{(} p, q, r \texttt{)}\!</math> looks like this: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Minimal Negation Operator (P,Q,R) ISW.jpg|500px]] | ||
| + | |} | ||
| + | |||
| + | In relation to the center cell indicated by the conjunction <math>pqr,\!</math> the region indicated by <math>\texttt{(} p, q, r \texttt{)}\!</math> is comprised of the adjacent or bordering cells. Thus they are the cells that are just across the boundary of the center cell, reached as if by way of Leibniz's ''minimal changes'' from the point of origin, in this case, <math>pqr.~\!</math> | ||
| + | |||
| + | More generally speaking, in a <math>k\!</math>-dimensional universe of discourse that is based on the ''alphabet'' of features <math>\mathcal{X} = \{ x_1, \ldots, x_k \},\!</math> the same form of boundary relationship is manifested for any cell of origin that one chooses to indicate. One way to indicate a cell is by forming a logical conjunction of positive and negative basis features, that is, by constructing an expression of the form <math>e_1 \cdot \ldots \cdot e_k,\!</math> where <math>e_j = x_j ~\text{or}~ e_j = \texttt{(} x_j \texttt{)},\!</math> for <math>j = 1 ~\text{to}~ k.\!</math> The proposition <math>\texttt{(} e_1, \ldots, e_k \texttt{)}\!</math> indicates the disjunctive region consisting of the cells that are just next door to <math>e_1 \cdot \ldots \cdot e_k.\!</math> | ||
| + | |||
| + | ==Goal-Oriented Systems== | ||
| + | |||
| + | I want to continue developing the basic tools of differential logic, which arose from exploring the connections between dynamics and logic, but I also wanted to give some hint of the applications that have motivated this work all along. One of these applications is to cybernetic systems, whether we see these systems as agents or cultures, individuals or species, organisms or organizations. | ||
| + | |||
| + | A cybernetic system has goals and actions for reaching them. It has a state space <math>X,\!</math> giving us all of the states that the system can be in, plus it has a goal space <math>G \subseteq X,\!</math> the set of states that the system “likes” to be in, in other words, the distinguished subset of possible states where the system is regarded as living, surviving, or thriving, depending on the type of goal that one has in mind for the system in question. As for actions, there is to begin with the full set <math>\mathcal{T}\!</math> of all possible actions, each of which is a transformation of the form <math>T : X \to X,\!</math> but a given cybernetic system will most likely have but a subset of these actions available to it at any given time. And even if we begin by thinking of actions in very general and very global terms, as arbitrarily complex transformations acting on the whole state space <math>X,\!</math> we quickly find a need to analyze and approximate them in terms of simple transformations acting locally. The preferred measure of “simplicity” will of course vary from one paradigm of research to another. | ||
| + | |||
| + | A generic enough picture at this stage of the game, and one that will remind us of these fundamental features of the cybernetic system even as things get far more complex, is afforded by Figure 23. | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | | ||
| + | <pre> | ||
| + | o---------------------------------------------------------------------o | ||
| + | | | | ||
| + | | X | | ||
| + | | o-------------------o | | ||
| + | | / \ | | ||
| + | | / \ | | ||
| + | | / \ | | ||
| + | | / \ | | ||
| + | | / \ | | ||
| + | | / \ | | ||
| + | | / \ | | ||
| + | | o G o | | ||
| + | | | | | | ||
| + | | | | | | ||
| + | | | | | | ||
| + | | | o<---------T---------o | | ||
| + | | | | | | ||
| + | | | | | | ||
| + | | | | | | ||
| + | | o o | | ||
| + | | \ / | | ||
| + | | \ / | | ||
| + | | \ / | | ||
| + | | \ / | | ||
| + | | \ / | | ||
| + | | \ / | | ||
| + | | \ / | | ||
| + | | o-------------------o | | ||
| + | | | | ||
| + | | | | ||
| + | o---------------------------------------------------------------------o | ||
| + | Figure 23. Elements of a Cybernetic System | ||
| + | </pre> | ||
| + | |} | ||
| + | |||
| + | ==Further Reading== | ||
| + | |||
| + | A more detailed presentation of Differential Logic can be found here: | ||
| + | |||
| + | :* [http://intersci.ss.uci.edu/wiki/index.php/Differential_Logic_and_Dynamic_Systems_2.0 Differential Logic and Dynamic Systems] | ||
| + | |||
| + | ==Document History== | ||
| + | |||
| + | ===Differential Logic • Ontology List 2002=== | ||
| + | |||
| + | * http://web.archive.org/web/20110612002240/http://suo.ieee.org/ontology/thrd28.html#04040 | ||
| + | # http://web.archive.org/web/20140406040004/http://suo.ieee.org/ontology/msg04040.html | ||
| + | # http://web.archive.org/web/20110612001949/http://suo.ieee.org/ontology/msg04041.html | ||
| + | # http://web.archive.org/web/20110612010502/http://suo.ieee.org/ontology/msg04045.html | ||
| + | # http://web.archive.org/web/20110612005212/http://suo.ieee.org/ontology/msg04046.html | ||
| + | # http://web.archive.org/web/20110612001954/http://suo.ieee.org/ontology/msg04047.html | ||
| + | # http://web.archive.org/web/20110612010620/http://suo.ieee.org/ontology/msg04048.html | ||
| + | # http://web.archive.org/web/20110612010550/http://suo.ieee.org/ontology/msg04052.html | ||
| + | # http://web.archive.org/web/20110612010724/http://suo.ieee.org/ontology/msg04054.html | ||
| + | # http://web.archive.org/web/20110612000847/http://suo.ieee.org/ontology/msg04055.html | ||
| + | # http://web.archive.org/web/20110612001959/http://suo.ieee.org/ontology/msg04067.html | ||
| + | # http://web.archive.org/web/20110612010507/http://suo.ieee.org/ontology/msg04068.html | ||
| + | # http://web.archive.org/web/20110612002014/http://suo.ieee.org/ontology/msg04069.html | ||
| + | # http://web.archive.org/web/20110612010701/http://suo.ieee.org/ontology/msg04070.html | ||
| + | # http://web.archive.org/web/20110612003540/http://suo.ieee.org/ontology/msg04072.html | ||
| + | # http://web.archive.org/web/20110612005229/http://suo.ieee.org/ontology/msg04073.html | ||
| + | # http://web.archive.org/web/20110610153117/http://suo.ieee.org/ontology/msg04074.html | ||
| + | # http://web.archive.org/web/20110612010555/http://suo.ieee.org/ontology/msg04077.html | ||
| + | # http://web.archive.org/web/20110612001918/http://suo.ieee.org/ontology/msg04079.html | ||
| + | # http://web.archive.org/web/20110612005244/http://suo.ieee.org/ontology/msg04080.html | ||
| + | # http://web.archive.org/web/20110612005249/http://suo.ieee.org/ontology/msg04268.html | ||
| + | # http://web.archive.org/web/20110612010626/http://suo.ieee.org/ontology/msg04269.html | ||
| + | # http://web.archive.org/web/20110612000853/http://suo.ieee.org/ontology/msg04272.html | ||
| + | # http://web.archive.org/web/20110612010514/http://suo.ieee.org/ontology/msg04273.html | ||
| + | # http://web.archive.org/web/20110612002235/http://suo.ieee.org/ontology/msg04290.html | ||
| + | |||
| + | ===Dynamics And Logic • Inquiry List 2004=== | ||
| + | |||
| + | * http://stderr.org/pipermail/inquiry/2004-May/thread.html#1400 | ||
| + | * http://stderr.org/pipermail/inquiry/2004-July/thread.html#1685 | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001400.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001401.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001402.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001403.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001404.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001405.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001406.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001407.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001408.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001410.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001411.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001412.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001413.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001415.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001416.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001418.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001419.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001420.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001421.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001422.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001423.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-May/001424.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-July/001685.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-July/001686.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-July/001687.html | ||
| + | # http://stderr.org/pipermail/inquiry/2004-July/001688.html | ||
| + | |||
| + | ===Dynamics And Logic • NKS Forum 2004=== | ||
| + | |||
| + | * http://forum.wolframscience.com/archive/topic/420.html | ||
| + | * http://forum.wolframscience.com/printthread.php?threadid=420 | ||
| + | * http://forum.wolframscience.com/showthread.php?threadid=420 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1282#post1282 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1285#post1285 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1289#post1289 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1292#post1292 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1293#post1293 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1294#post1294 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1296#post1296 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1299#post1299 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1301#post1301 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1304#post1304 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1307#post1307 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1309#post1309 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1311#post1311 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1314#post1314 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1315#post1315 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1318#post1318 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1321#post1321 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1323#post1323 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1326#post1326 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1327#post1327 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1330#post1330 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1331#post1331 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1598#post1598 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1601#post1601 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1602#post1602 | ||
| + | # http://forum.wolframscience.com/showthread.php?postid=1603#post1603 | ||
| + | |||
| + | [[Category:Artificial Intelligence]] | ||
| + | [[Category:Boolean Algebra]] | ||
| + | [[Category:Boolean Functions]] | ||
| + | [[Category:Charles Sanders Peirce]] | ||
| + | [[Category:Combinatorics]] | ||
| + | [[Category:Computational Complexity]] | ||
| + | [[Category:Computer Science]] | ||
| + | [[Category:Cybernetics]] | ||
| + | [[Category:Differential Logic]] | ||
| + | [[Category:Equational Reasoning]] | ||
| + | [[Category:Formal Languages]] | ||
| + | [[Category:Formal Systems]] | ||
| + | [[Category:Graph Theory]] | ||
| + | [[Category:Inquiry]] | ||
| + | [[Category:Inquiry Driven Systems]] | ||
| + | [[Category:Knowledge Representation]] | ||
| + | [[Category:Logic]] | ||
| + | [[Category:Logical Graphs]] | ||
| + | [[Category:Mathematics]] | ||
| + | [[Category:Philosophy]] | ||
| + | [[Category:Propositional Calculus]] | ||
| + | [[Category:Semiotics]] | ||
| + | [[Category:Visualization]] | ||
| + | |||
==Notes & Queries== | ==Notes & Queries== | ||
Revision as of 18:20, 4 December 2015
Author: Jon Awbrey
Differential logic is the component of logic whose object is the description of variation — for example, the aspects of change, difference, distribution, and diversity — in universes of discourse that are subject to logical description. A definition that broad naturally incorporates any study of variation by way of mathematical models, but differential logic is especially charged with the qualitative aspects of variation that pervade or precede quantitative models. To the extent that a logical inquiry makes use of a formal system, its differential component treats the principles that govern the use of a differential logical calculus, that is, a formal system with the expressive capacity to describe change and diversity in a logical universe of discourse.
A simple example of a differential logical calculus is furnished by a differential propositional calculus. A differential propositional calculus is a propositional calculus extended by a set of terms for describing aspects of change and difference, for example, processes that take place in a universe of discourse or transformations that map a source universe into a target universe. This augments ordinary propositional calculus in the same way that the differential calculus of Leibniz and Newton augments the analytic geometry of Descartes.
Quick Overview
Cactus Language for Propositional Logic
The development of differential logic is greatly facilitated by having a conceptually efficient calculus in place at the level of boolean-valued functions and elementary logical propositions. A calculus that is very efficient from both conceptual and computational standpoints is based on just two types of logical connectives, both of variable \(k\!\)-ary scope. The formulas of this calculus map into a species of graph-theoretical structures called painted and rooted cacti (PARCs) that lend visual representation to their functional structure and smooth the path to efficient computation.
| The first kind of propositional expression is a parenthesized sequence of propositional expressions, written as \(\texttt{(} e_1 \texttt{,} e_2 \texttt{,} \ldots \texttt{,} e_{k-1} \texttt{,} e_k \texttt{)}\!\) and read to say that exactly one of the propositions \(e_1, e_2, \ldots, e_{k-1}, e_k\!\) is false, in other words, that their minimal negation is true. A clause of this form maps into a PARC structure called a lobe, in this case, one that is painted with the colors \(e_1, e_2, \ldots, e_{k-1}, e_k\!\) as shown below. |
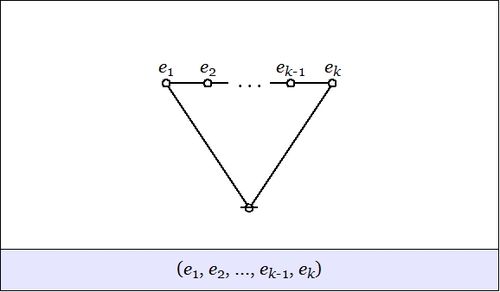
|
| The second kind of propositional expression is a concatenated sequence of propositional expressions, written as \(e_1\ e_2\ \ldots\ e_{k-1}\ e_k\!\) and read to say that all of the propositions \(e_1, e_2, \ldots, e_{k-1}, e_k\!\) are true, in other words, that their logical conjunction is true. A clause of this form maps into a PARC structure called a node, in this case, one that is painted with the colors \(e_1, e_2, \ldots, e_{k-1}, e_k\!\) as shown below. |

|
All other propositional connectives can be obtained through combinations of these two forms. Strictly speaking, the parenthesized form is sufficient to define the concatenated form, making the latter formally dispensable, but it is convenient to maintain it as a concise way of expressing more complicated combinations of parenthesized forms. While working with expressions solely in propositional calculus, it is easiest to use plain parentheses for logical connectives. In contexts where ordinary parentheses are needed for other purposes an alternate typeface \(\texttt{(} \ldots \texttt{)}\!\) may be used for logical operators.
Table 1 collects a sample of basic propositional forms as expressed in terms of cactus language connectives.
The simplest expression for logical truth is the empty word, usually denoted by \(\boldsymbol\varepsilon\!\) or \(\lambda\!\) in formal languages, where it forms the identity element for concatenation. To make it visible in context, it may be denoted by the equivalent expression \({}^{\backprime\backprime} \texttt{((}~\texttt{))} {}^{\prime\prime},\!\) or, especially if operating in an algebraic context, by a simple \({}^{\backprime\backprime} 1 {}^{\prime\prime}.\!\) Also when working in an algebraic mode, the plus sign \({}^{\backprime\backprime} + {}^{\prime\prime}\!\) may be used for exclusive disjunction. For example, we have the following paraphrases of algebraic expressions by means of parenthesized expressions:
|
\(\begin{matrix} a + b & = & \texttt{(} a \texttt{,} b \texttt{)} \end{matrix}\!\) |
|
\(\begin{matrix} a + b + c & = & \texttt{(} a \texttt{,(} b \texttt{,} c \texttt{))} & = & \texttt{((} a \texttt{,} b \texttt{),} c \texttt{)} \end{matrix}\!\) |
It is important to note that the last expressions are not equivalent to the 3-place parenthesis \(\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}.\!\)
Differential Expansions of Propositions
Bird's Eye View
An efficient calculus for the realm of logic represented by boolean functions and elementary propositions makes it feasible to compute the finite differences and the differentials of those functions and propositions.
For example, consider a proposition of the form \({}^{\backprime\backprime} \, p ~\mathrm{and}~ q \, {}^{\prime\prime}\!\) that is graphed as two letters attached to a root node:

|
Written as a string, this is just the concatenation \(p~q\!\).
The proposition \(pq\!\) may be taken as a boolean function \(f(p, q)\!\) having the abstract type \(f : \mathbb{B} \times \mathbb{B} \to \mathbb{B},\!\) where \(\mathbb{B} = \{ 0, 1 \}~\!\) is read in such a way that \(0\!\) means \(\mathrm{false}\!\) and \(1\!\) means \(\mathrm{true}.\!\)
Imagine yourself standing in a fixed cell of the corresponding venn diagram, say, the cell where the proposition \(pq\!\) is true, as shown in the following Figure:
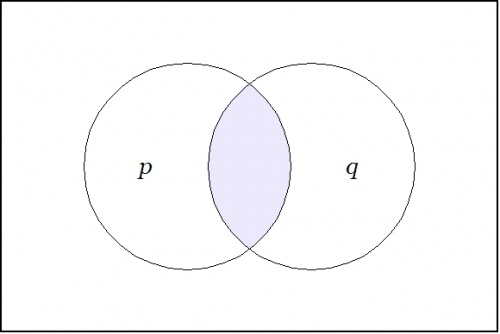
|
Now ask yourself: What is the value of the proposition \(pq\!\) at a distance of \(\mathrm{d}p\!\) and \(\mathrm{d}q\!\) from the cell \(pq\!\) where you are standing?
Don't think about it — just compute:
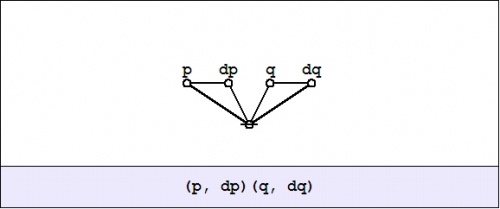
|
The cactus formula \(\texttt{(p, dp)(q, dq)}\!\) and its corresponding graph arise by substituting \(p + \mathrm{d}p\!\) for \(p\!\) and \(q + \mathrm{d}q\!\) for \(q\!\) in the boolean product or logical conjunction \(pq\!\) and writing the result in the two dialects of cactus syntax. This follows from the fact that the boolean sum \(p + \mathrm{d}p\!\) is equivalent to the logical operation of exclusive disjunction, which parses to a cactus graph of the following form:
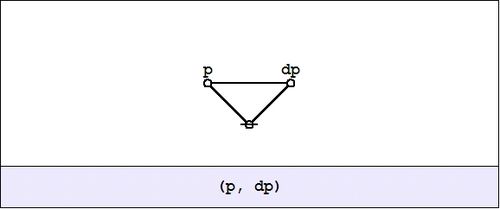
|
Next question: What is the difference between the value of the proposition \(pq\!\) over there, at a distance of \(\mathrm{d}p\!\) and \(\mathrm{d}q,\!\) and the value of the proposition \(pq\!\) where you are standing, all expressed in the form of a general formula, of course? Here is the appropriate formulation:
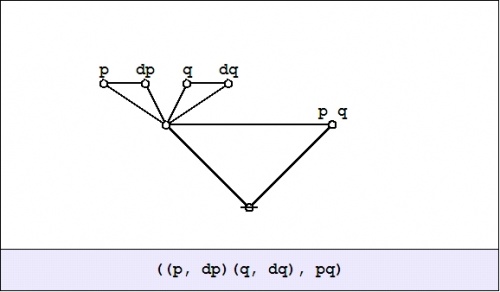
|
There is one thing that I ought to mention at this point: Computed over \(\mathbb{B},\!\) plus and minus are identical operations. This will make the relation between the differential and the integral parts of the appropriate calculus slightly stranger than usual, but we will get into that later.
Last question, for now: What is the value of this expression from your current standpoint, that is, evaluated at the point where \(pq\!\) is true? Well, substituting \(1\!\) for \(p\!\) and \(1\!\) for \(q\!\) in the graph amounts to erasing the labels \(p\!\) and \(q\!,\!\) as shown here:
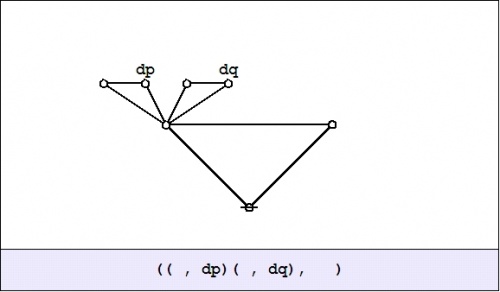
|
And this is equivalent to the following graph:
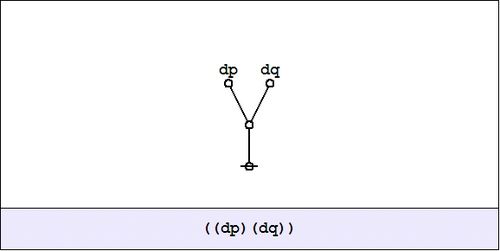
|
We have just met with the fact that the differential of the and is the or of the differentials.
|
\(\begin{matrix} p ~\mathrm{and}~ q & \quad & \xrightarrow{\quad\mathrm{Diff}\quad} & \quad & \mathrm{d}p ~\mathrm{or}~ \mathrm{d}q \end{matrix}\!\) |
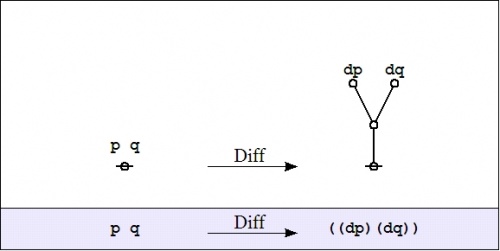
|
It will be necessary to develop a more refined analysis of that statement directly, but that is roughly the nub of it.
If the form of the above statement reminds you of De Morgan's rule, it is no accident, as differentiation and negation turn out to be closely related operations. Indeed, one can find discussions of logical difference calculus in the Boole–De Morgan correspondence and Peirce also made use of differential operators in a logical context, but the exploration of these ideas has been hampered by a number of factors, not the least of which has been the lack of a syntax that was adequate to handle the complexity of expressions that evolve.
Worm's Eye View
Let's run through the initial example again, this time attempting to interpret the formulas that develop at each stage along the way. We begin with a proposition or a boolean function \(f(p, q) = pq.\!\)
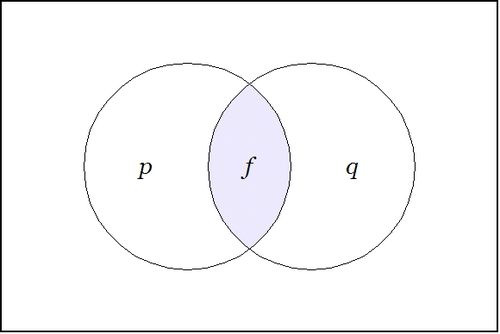
|
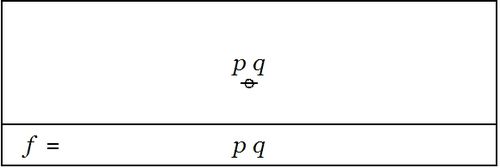
|
A function like this has an abstract type and a concrete type. The abstract type is what we invoke when we write things like \(f : \mathbb{B} \times \mathbb{B} \to \mathbb{B}\!\) or \(f : \mathbb{B}^2 \to \mathbb{B}.\!\) The concrete type takes into account the qualitative dimensions or the “units” of the case, which can be explained as follows.
| Let \(P\!\) be the set of values \(\{ \texttt{(} p \texttt{)},~ p \} ~=~ \{ \mathrm{not}~ p,~ p \} ~\cong~ \mathbb{B}.\!\) |
| Let \(Q\!\) be the set of values \(\{ \texttt{(} q \texttt{)},~ q \} ~=~ \{ \mathrm{not}~ q,~ q \} ~\cong~ \mathbb{B}.\!\) |
Then interpret the usual propositions about \(p, q\!\) as functions of the concrete type \(f : P \times Q \to \mathbb{B}.\!\)
We are going to consider various operators on these functions. Here, an operator \(\mathrm{F}\!\) is a function that takes one function \(f\!\) into another function \(\mathrm{F}f.\!\)
The first couple of operators that we need to consider are logical analogues of the pair that play a founding role in the classical finite difference calculus, namely:
| The difference operator \(\Delta,\!\) written here as \(\mathrm{D}.\!\) |
| The enlargement operator \(\Epsilon,\!\) written here as \(\mathrm{E}.\!\) |
These days, \(\mathrm{E}\!\) is more often called the shift operator.
In order to describe the universe in which these operators operate, it is necessary to enlarge the original universe of discourse. Starting from the initial space \(X = P \times Q,\!\) its (first order) differential extension \(\mathrm{E}X\!\) is constructed according to the following specifications:
|
\(\begin{array}{rcc} \mathrm{E}X & = & X \times \mathrm{d}X \end{array}\!\) |
where:
|
\(\begin{array}{rcc} X & = & P \times Q \\[4pt] \mathrm{d}X & = & \mathrm{d}P \times \mathrm{d}Q \\[4pt] \mathrm{d}P & = & \{ \texttt{(} \mathrm{d}p \texttt{)},~ \mathrm{d}p \} \\[4pt] \mathrm{d}Q & = & \{ \texttt{(} \mathrm{d}q \texttt{)},~ \mathrm{d}q \} \end{array}\!\) |
The interpretations of these new symbols can be diverse, but the easiest option for now is just to say that \(\mathrm{d}p\!\) means “change \(p\!\)” and \(\mathrm{d}q\!\) means “change \(q\!\)”.
Drawing a venn diagram for the differential extension \(\mathrm{E}X = X \times \mathrm{d}X\!\) requires four logical dimensions, \(P, Q, \mathrm{d}P, \mathrm{d}Q,\!\) but it is possible to project a suggestion of what the differential features \(\mathrm{d}p\!\) and \(\mathrm{d}q\!\) are about on the 2-dimensional base space \(X = P \times Q\!\) by drawing arrows that cross the boundaries of the basic circles in the venn diagram for \(X,\!\) reading an arrow as \(\mathrm{d}p\!\) if it crosses the boundary between \(p\!\) and \(\texttt{(} p \texttt{)}\!\) in either direction and reading an arrow as \(\mathrm{d}q\!\) if it crosses the boundary between \(q\!\) and \(\texttt{(} q \texttt{)}\!\) in either direction.
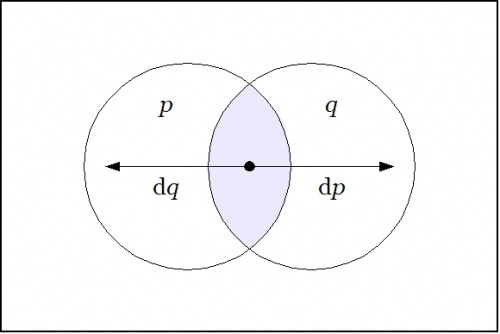
|
Propositions are formed on differential variables, or any combination of ordinary logical variables and differential logical variables, in the same ways that propositions are formed on ordinary logical variables alone. For example, the proposition \(\texttt{(} \mathrm{d}p \texttt{(} \mathrm{d}q \texttt{))}\!\) says the same thing as \(\mathrm{d}p \Rightarrow \mathrm{d}q,\!\) in other words, that there is no change in \(p\!\) without a change in \(q.\!\)
Given the proposition \(f(p, q)\!\) over the space \(X = P \times Q,\!\) the (first order) enlargement of \(f\!\) is the proposition \(\mathrm{E}f\!\) over the differential extension \(\mathrm{E}X\!\) that is defined by the following formula:
|
\(\begin{matrix} \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) & = & f(p + \mathrm{d}p,~ q + \mathrm{d}q) & = & f( \texttt{(} p, \mathrm{d}p \texttt{)},~ \texttt{(} q, \mathrm{d}q \texttt{)} ) \end{matrix}\!\) |
In the example \(f(p, q) = pq,\!\) the enlargement \(\mathrm{E}f\!\) is computed as follows:
|
\(\begin{matrix} \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) & = & (p + \mathrm{d}p)(q + \mathrm{d}q) & = & \texttt{(} p, \mathrm{d}p \texttt{)(} q, \mathrm{d}q \texttt{)} \end{matrix}\!\) |
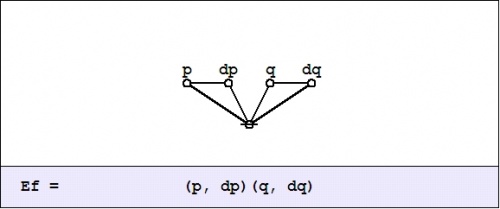
|
Given the proposition \(f(p, q)\!\) over \(X = P \times Q,\!\) the (first order) difference of \(f\!\) is the proposition \(\mathrm{D}f~\!\) over \(\mathrm{E}X\!\) that is defined by the formula \(\mathrm{D}f = \mathrm{E}f - f,\!\) or, written out in full:
|
\(\begin{matrix} \mathrm{D}f(p, q, \mathrm{d}p, \mathrm{d}q) & = & f(p + \mathrm{d}p,~ q + \mathrm{d}q) - f(p, q) & = & \texttt{(} f( \texttt{(} p, \mathrm{d}p \texttt{)},~ \texttt{(} q, \mathrm{d}q \texttt{)} ),~ f(p, q) \texttt{)} \end{matrix}\!\) |
In the example \(f(p, q) = pq,\!\) the difference \(\mathrm{D}f~\!\) is computed as follows:
We did not yet go through the trouble to interpret this (first order) difference of conjunction fully, but were happy simply to evaluate it with respect to a single location in the universe of discourse, namely, at the point picked out by the singular proposition \(pq,\!\) that is, at the place where \(p = 1\!\) and \(q = 1.\!\) This evaluation is written in the form \(\mathrm{D}f|_{pq}\!\) or \(\mathrm{D}f|_{(1, 1)},\!\) and we arrived at the locally applicable law that is stated and illustrated as follows:
|
\(f(p, q) ~=~ pq ~=~ p ~\mathrm{and}~ q \quad \Rightarrow \quad \mathrm{D}f|_{pq} ~=~ \texttt{((} \mathrm{dp} \texttt{)(} \mathrm{d}q \texttt{))} ~=~ \mathrm{d}p ~\mathrm{or}~ \mathrm{d}q\!\) |
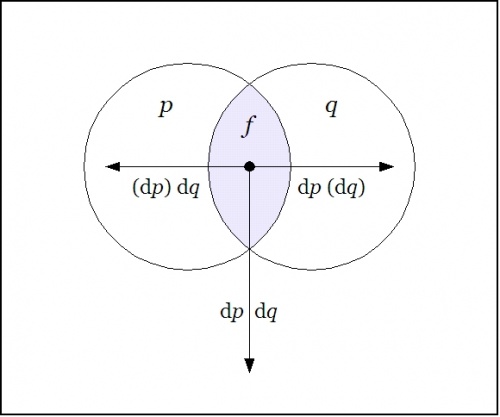
|
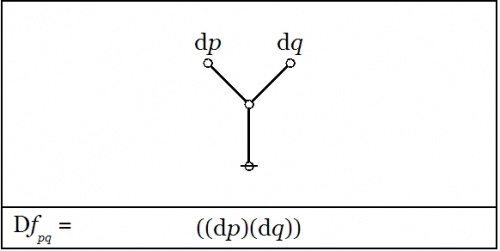
|
The picture shows the analysis of the inclusive disjunction \(\texttt{((} \mathrm{d}p \texttt{)(} \mathrm{d}q \texttt{))}\!\) into the following exclusive disjunction:
|
\(\begin{matrix} \mathrm{d}p ~\texttt{(} \mathrm{d}q \texttt{)} & + & \texttt{(} \mathrm{d}p \texttt{)}~ \mathrm{d}q & + & \mathrm{d}p ~\mathrm{d}q \end{matrix}\!\) |
The differential proposition that results may be interpreted to say “change \(p\!\) or change \(q\!\) or both”. And this can be recognized as just what you need to do if you happen to find yourself in the center cell and require a complete and detailed description of ways to escape it.
Last time we computed what is variously called the difference map, the difference proposition, or the local proposition \(\mathrm{D}f_x\!\) of the proposition \(f(p, q) = pq\!\) at the point \(x\!\) where \(p = 1\!\) and \(q = 1.\!\)
In the universe \(X = P \times Q,\!\) the four propositions \(pq,~ p \texttt{(} q \texttt{)},~ \texttt{(} p \texttt{)} q,~ \texttt{(} p \texttt{)(} q \texttt{)}\!\) that indicate the “cells”, or the smallest regions of the venn diagram, are called singular propositions. These serve as an alternative notation for naming the points \((1, 1),~ (1, 0),~ (0, 1),~ (0, 0),\!\) respectively.
Thus we can write \(\mathrm{D}f_x = \mathrm{D}f|x = \mathrm{D}f|(1, 1) = \mathrm{D}f|pq,\!\) so long as we know the frame of reference in force.
In the example \(f(p, q) = pq,\!\) the value of the difference proposition \(\mathrm{D}f_x\!\) at each of the four points in \(x \in X\!\) may be computed in graphical fashion as shown below:
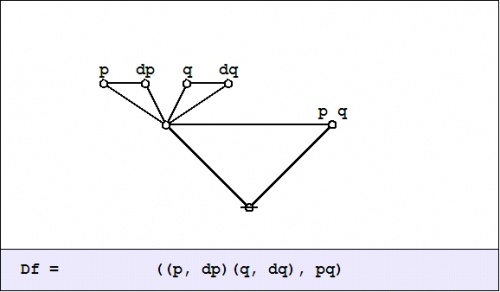
|
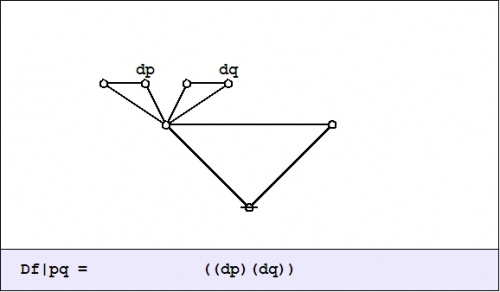
|
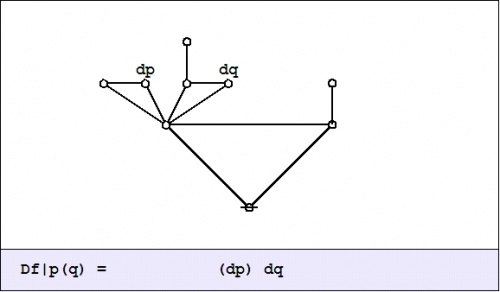
|
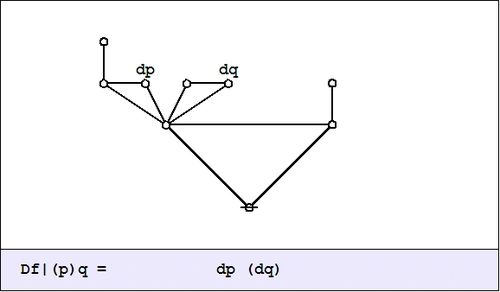
|
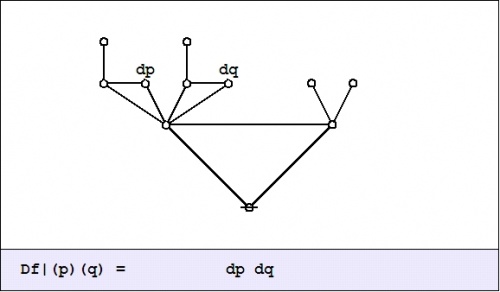
|
The easy way to visualize the values of these graphical expressions is just to notice the following equivalents:
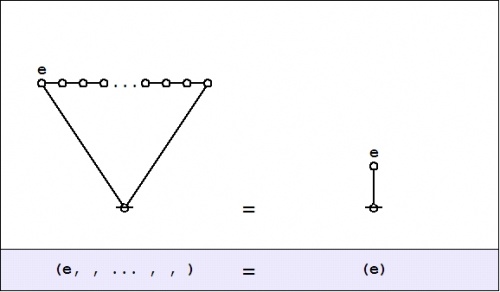
|
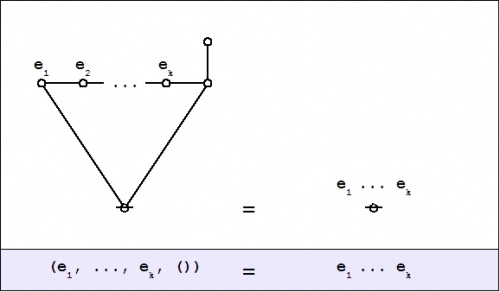
|
Laying out the arrows on the augmented venn diagram, one gets a picture of a differential vector field.
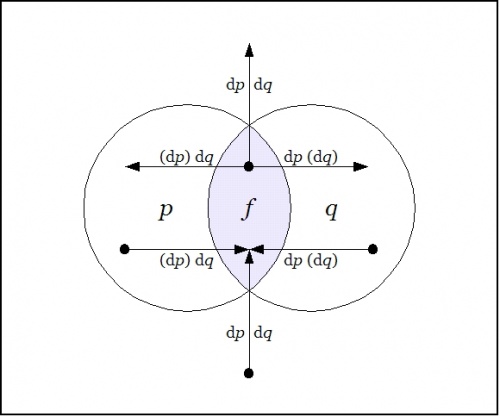
|
The Figure shows the points of the extended universe \(\mathrm{E}X = P \times Q \times \mathrm{d}P \times \mathrm{d}Q\!\) that are indicated by the difference map \(\mathrm{D}f : \mathrm{E}X \to \mathbb{B},\!\) namely, the following six points or singular propositions::
|
\(\begin{array}{rcccc} 1. & p & q & \mathrm{d}p & \mathrm{d}q \\ 2. & p & q & \mathrm{d}p & (\mathrm{d}q) \\ 3. & p & q & (\mathrm{d}p) & \mathrm{d}q \\ 4. & p & (q) & (\mathrm{d}p) & \mathrm{d}q \\ 5. & (p) & q & \mathrm{d}p & (\mathrm{d}q) \\ 6. & (p) & (q) & \mathrm{d}p & \mathrm{d}q \end{array}\!\) |
The information borne by \(\mathrm{D}f~\!\) should be clear enough from a survey of these six points — they tell you what you have to do from each point of \(X\!\) in order to change the value borne by \(f(p, q),\!\) that is, the move you have to make in order to reach a point where the value of the proposition \(f(p, q)\!\) is different from what it is where you started.
We have been studying the action of the difference operator \(\mathrm{D}\!\) on propositions of the form \(f : P \times Q \to \mathbb{B},\!\) as illustrated by the example \(f(p, q) = pq\!\) that is known in logic as the conjunction of \(p\!\) and \(q.\!\) The resulting difference map \(\mathrm{D}f~\!\) is a (first order) differential proposition, that is, a proposition of the form \(\mathrm{D}f : P \times Q \times \mathrm{d}P \times \mathrm{d}Q \to \mathbb{B}.\!\)
Abstracting from the augmented venn diagram that shows how the models or satisfying interpretations of \(\mathrm{D}f~\!\) distribute over the extended universe of discourse \(\mathrm{E}X = P \times Q \times \mathrm{d}P \times \mathrm{d}Q,\!\) the difference map \(\mathrm{D}f~\!\) can be represented in the form of a digraph or directed graph, one whose points are labeled with the elements of \(X = P \times Q\!\) and whose arrows are labeled with the elements of \(\mathrm{d}X = \mathrm{d}P \times \mathrm{d}Q,\!\) as shown in the following Figure.
Any proposition worth its salt can be analyzed from many different points of view, any one of which has the potential to reveal an unsuspected aspect of the proposition's meaning. We will encounter more and more of these alternative readings as we go.
The enlargement or shift operator \(\mathrm{E}\!\) exhibits a wealth of interesting and useful properties in its own right, so it pays to examine a few of the more salient features that play out on the surface of our initial example, \(f(p, q) = pq.\!\)
A suitably generic definition of the extended universe of discourse is afforded by the following set-up:
|
\(\begin{array}{lccl} \text{Let} & X & = & X_1 \times \ldots \times X_k. \\[6pt] \text{Let} & \mathrm{d}X & = & \mathrm{d}X_1 \times \ldots \times \mathrm{d}X_k. \\[6pt] \text{Then} & \mathrm{E}X & = & X \times \mathrm{d}X \\[6pt] & & = & X_1 \times \ldots \times X_k ~\times~ \mathrm{d}X_1 \times \ldots \times \mathrm{d}X_k \end{array}\!\) |
For a proposition of the form \(f : X_1 \times \ldots \times X_k \to \mathbb{B},\!\) the (first order) enlargement of \(f\!\) is the proposition \(\mathrm{E}f : \mathrm{E}X \to \mathbb{B}\!\) that is defined by the following equation:
|
\(\begin{array}{l} \mathrm{E}f(x_1, \ldots, x_k, \mathrm{d}x_1, \ldots, \mathrm{d}x_k) \\[6pt] = \quad f(x_1 + \mathrm{d}x_1, \ldots, x_k + \mathrm{d}x_k) \\[6pt] = \quad f( \texttt{(} x_1, \mathrm{d}x_1 \texttt{)}, \ldots, \texttt{(} x_k, \mathrm{d}x_k \texttt{)} ) \end{array}\!\) |
The differential variables \(\mathrm{d}x_j\!\) are boolean variables of the same basic type as the ordinary variables \(x_j.\!\) Although it is conventional to distinguish the (first order) differential variables with the operative prefix “\(\mathrm{d}\!\)” this way of notating differential variables is entirely optional. It is their existence in particular relations to the initial variables, not their names, that defines them as differential variables.
In the example of logical conjunction, \(f(p, q) = pq,\!\) the enlargement \(\mathrm{E}f\!\) is formulated as follows:
|
\(\begin{array}{l} \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) \\[6pt] = \quad (p + \mathrm{d}p)(q + \mathrm{d}q) \\[6pt] = \quad \texttt{(} p, \mathrm{d}p \texttt{)(} q, \mathrm{d}q \texttt{)} \end{array}\!\) |
Given that this expression uses nothing more than the boolean ring operations of addition and multiplication, it is permissible to “multiply things out” in the usual manner to arrive at the following result:
|
\(\begin{matrix} \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) & = & p~q & + & p~\mathrm{d}q & + & q~\mathrm{d}p & + & \mathrm{d}p~\mathrm{d}q \end{matrix}\!\) |
To understand what the enlarged or shifted proposition means in logical terms, it serves to go back and analyze the above expression for \(\mathrm{E}f\!\) in the same way that we did for \(\mathrm{D}f.\!\) Toward that end, the value of \(\mathrm{E}f_x\!\) at each \(x \in X\!\) may be computed in graphical fashion as shown below:

|
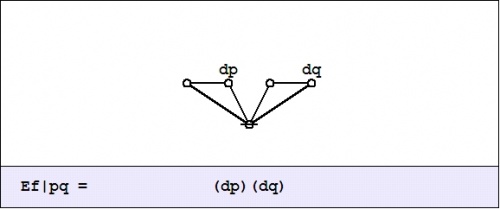
|
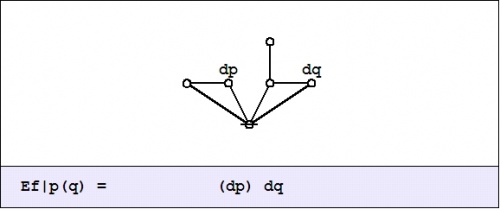
|
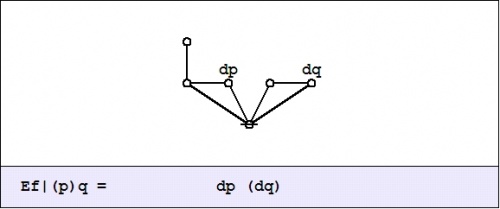
|
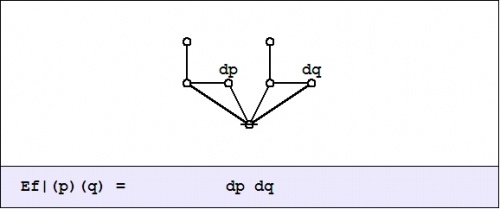
|
Given the data that develops in this form of analysis, the disjoined ingredients can now be folded back into a boolean expansion or a disjunctive normal form (DNF) that is equivalent to the enlarged proposition \(\mathrm{E}f.\!\)
|
\(\begin{matrix} \mathrm{E}f & = & pq \cdot \mathrm{E}f_{pq} & + & p(q) \cdot \mathrm{E}f_{p(q)} & + & (p)q \cdot \mathrm{E}f_{(p)q} & + & (p)(q) \cdot \mathrm{E}f_{(p)(q)} \end{matrix}\!\) |
Here is a summary of the result, illustrated by means of a digraph picture, where the “no change” element \((\mathrm{d}p)(\mathrm{d}q)\!\) is drawn as a loop at the point \(p~q.\!\)
We may understand the enlarged proposition \(\mathrm{E}f\!\) as telling us all the different ways to reach a model of the proposition \(f\!\) from each point of the universe \(X.\!\)
Propositional Forms on Two Variables
To broaden our experience with simple examples, let us examine the sixteen functions of concrete type \(P \times Q \to \mathbb{B}\!\) and abstract type \(\mathbb{B} \times \mathbb{B} \to \mathbb{B}.\!\) A few Tables are set here that detail the actions of \(\mathrm{E}\!\) and \(\mathrm{D}\!\) on each of these functions, allowing us to view the results in several different ways.
Tables A1 and A2 show two ways of arranging the 16 boolean functions on two variables, giving equivalent expressions for each function in several different systems of notation.
|
\(\mathcal{L}_1\!\) \(\text{Decimal}\!\) |
\(\mathcal{L}_2\!\) \(\text{Binary}\!\) |
\(\mathcal{L}_3\!\) \(\text{Vector}\!\) |
\(\mathcal{L}_4\!\) \(\text{Cactus}\!\) |
\(\mathcal{L}_5\!\) \(\text{English}\!\) |
\(\mathcal{L}_6~\!\) \(\text{Ordinary}\!\) |
| \(p\colon\!\) | \(1~1~0~0\!\) | ||||
| \(q\colon\!\) | \(1~0~1~0\!\) | ||||
|
\(\begin{matrix} f_0 \\[4pt] f_1 \\[4pt] f_2 \\[4pt] f_3 \\[4pt] f_4 \\[4pt] f_5 \\[4pt] f_6 \\[4pt] f_7 \end{matrix}\!\) |
\(\begin{matrix} f_{0000} \\[4pt] f_{0001} \\[4pt] f_{0010} \\[4pt] f_{0011} \\[4pt] f_{0100} \\[4pt] f_{0101} \\[4pt] f_{0110} \\[4pt] f_{0111} \end{matrix}\!\) |
\(\begin{matrix} 0~0~0~0 \\[4pt] 0~0~0~1 \\[4pt] 0~0~1~0 \\[4pt] 0~0~1~1 \\[4pt] 0~1~0~0 \\[4pt] 0~1~0~1 \\[4pt] 0~1~1~0 \\[4pt] 0~1~1~1 \end{matrix}\!\) |
\(\begin{matrix} (~) \\[4pt] (p)(q) \\[4pt] (p)~q~ \\[4pt] (p)~ ~ \\[4pt] ~p~(q) \\[4pt] ~ ~(q) \\[4pt] (p,~q) \\[4pt] (p~~q) \end{matrix}\!\) |
\(\begin{matrix} \text{false} \\[4pt] \text{neither}~ p ~\text{nor}~ q \\[4pt] q ~\text{without}~ p \\[4pt] \text{not}~ p \\[4pt] p ~\text{without}~ q \\[4pt] \text{not}~ q \\[4pt] p ~\text{not equal to}~ q \\[4pt] \text{not both}~ p ~\text{and}~ q \end{matrix}\!\) |
\(\begin{matrix} 0 \\[4pt] \lnot p \land \lnot q \\[4pt] \lnot p \land q \\[4pt] \lnot p \\[4pt] p \land \lnot q \\[4pt] \lnot q \\[4pt] p \ne q \\[4pt] \lnot p \lor \lnot q \end{matrix}\!\) |
|
\(\begin{matrix} f_8 \\[4pt] f_9 \\[4pt] f_{10} \\[4pt] f_{11} \\[4pt] f_{12} \\[4pt] f_{13} \\[4pt] f_{14} \\[4pt] f_{15} \end{matrix}\!\) |
\(\begin{matrix} f_{1000} \\[4pt] f_{1001} \\[4pt] f_{1010} \\[4pt] f_{1011} \\[4pt] f_{1100} \\[4pt] f_{1101} \\[4pt] f_{1110} \\[4pt] f_{1111} \end{matrix}\!\) |
\(\begin{matrix} 1~0~0~0 \\[4pt] 1~0~0~1 \\[4pt] 1~0~1~0 \\[4pt] 1~0~1~1 \\[4pt] 1~1~0~0 \\[4pt] 1~1~0~1 \\[4pt] 1~1~1~0 \\[4pt] 1~1~1~1 \end{matrix}\!\) |
\(\begin{matrix} ~~p~~q~~ \\[4pt] ((p,~q)) \\[4pt] ~ ~ ~q~~ \\[4pt] ~(p~(q)) \\[4pt] ~~p~ ~ ~ \\[4pt] ((p)~q)~ \\[4pt] ((p)(q)) \\[4pt] ((~)) \end{matrix}\!\) |
\(\begin{matrix} p ~\text{and}~ q \\[4pt] p ~\text{equal to}~ q \\[4pt] q \\[4pt] \text{not}~ p ~\text{without}~ q \\[4pt] p \\[4pt] \text{not}~ q ~\text{without}~ p \\[4pt] p ~\text{or}~ q \\[4pt] \text{true} \end{matrix}\!\) |
\(\begin{matrix} p \land q \\[4pt] p = q \\[4pt] q \\[4pt] p \Rightarrow q \\[4pt] p \\[4pt] p \Leftarrow q \\[4pt] p \lor q \\[4pt] 1 \end{matrix}\!\) |
|
\(\mathcal{L}_1\!\) \(\text{Decimal}\!\) |
\(\mathcal{L}_2\!\) \(\text{Binary}\!\) |
\(\mathcal{L}_3\!\) \(\text{Vector}\!\) |
\(\mathcal{L}_4\!\) \(\text{Cactus}\!\) |
\(\mathcal{L}_5\!\) \(\text{English}\!\) |
\(\mathcal{L}_6~\!\) \(\text{Ordinary}\!\) |
| \(p\colon\!\) | \(1~1~0~0\!\) | ||||
| \(q\colon\!\) | \(1~0~1~0\!\) | ||||
| \(f_0\!\) | \(f_{0000}\!\) | \(0~0~0~0\!\) | \((~)\!\) | \(\text{false}\!\) | \(0\!\) |
|
\(\begin{matrix} f_1 \\[4pt] f_2 \\[4pt] f_4 \\[4pt] f_8 \end{matrix}\!\) |
\(\begin{matrix} f_{0001} \\[4pt] f_{0010} \\[4pt] f_{0100} \\[4pt] f_{1000} \end{matrix}\!\) |
\(\begin{matrix} 0~0~0~1 \\[4pt] 0~0~1~0 \\[4pt] 0~1~0~0 \\[4pt] 1~0~0~0 \end{matrix}\!\) |
\(\begin{matrix} (p)(q) \\[4pt] (p)~q~ \\[4pt] ~p~(q) \\[4pt] ~p~~q~ \end{matrix}\!\) |
\(\begin{matrix} \text{neither}~ p ~\text{nor}~ q \\[4pt] q ~\text{without}~ p \\[4pt] p ~\text{without}~ q \\[4pt] p ~\text{and}~ q \end{matrix}\!\) |
\(\begin{matrix} \lnot p \land \lnot q \\[4pt] \lnot p \land q \\[4pt] p \land \lnot q \\[4pt] p \land q \end{matrix}\!\) |
|
\(\begin{matrix} f_3 \\[4pt] f_{12} \end{matrix}\!\) |
\(\begin{matrix} f_{0011} \\[4pt] f_{1100} \end{matrix}\!\) |
\(\begin{matrix} 0~0~1~1 \\[4pt] 1~1~0~0 \end{matrix}\!\) |
\(\begin{matrix} (p) \\[4pt] ~p~ \end{matrix}\!\) |
\(\begin{matrix} \text{not}~ p \\[4pt] p \end{matrix}\!\) |
\(\begin{matrix} \lnot p \\[4pt] p \end{matrix}\!\) |
|
\(\begin{matrix} f_6 \\[4pt] f_9 \end{matrix}\!\) |
\(\begin{matrix} f_{0110} \\[4pt] f_{1001} \end{matrix}\!\) |
\(\begin{matrix} 0~1~1~0 \\[4pt] 1~0~0~1 \end{matrix}\!\) |
\(\begin{matrix} ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
\(\begin{matrix} p ~\text{not equal to}~ q \\[4pt] p ~\text{equal to}~ q \end{matrix}\!\) |
\(\begin{matrix} p \ne q \\[4pt] p = q \end{matrix}\!\) |
|
\(\begin{matrix} f_5 \\[4pt] f_{10} \end{matrix}\!\) |
\(\begin{matrix} f_{0101} \\[4pt] f_{1010} \end{matrix}\!\) |
\(\begin{matrix} 0~1~0~1 \\[4pt] 1~0~1~0 \end{matrix}\!\) |
\(\begin{matrix} (q) \\[4pt] ~q~ \end{matrix}\!\) |
\(\begin{matrix} \text{not}~ q \\[4pt] q \end{matrix}\!\) |
\(\begin{matrix} \lnot q \\[4pt] q \end{matrix}\!\) |
|
\(\begin{matrix} f_7 \\[4pt] f_{11} \\[4pt] f_{13} \\[4pt] f_{14} \end{matrix}\!\) |
\(\begin{matrix} f_{0111} \\[4pt] f_{1011} \\[4pt] f_{1101} \\[4pt] f_{1110} \end{matrix}\!\) |
\(\begin{matrix} 0~1~1~1 \\[4pt] 1~0~1~1 \\[4pt] 1~1~0~1 \\[4pt] 1~1~1~0 \end{matrix}\!\) |
\(\begin{matrix} ~(p~~q)~ \\[4pt] ~(p~(q)) \\[4pt] ((p)~q)~ \\[4pt] ((p)(q)) \end{matrix}\!\) |
\(\begin{matrix} \text{not both}~ p ~\text{and}~ q \\[4pt] \text{not}~ p ~\text{without}~ q \\[4pt] \text{not}~ q ~\text{without}~ p \\[4pt] p ~\text{or}~ q \end{matrix}\!\) |
\(\begin{matrix} \lnot p \lor \lnot q \\[4pt] p \Rightarrow q \\[4pt] p \Leftarrow q \\[4pt] p \lor q \end{matrix}\!\) |
| \(f_{15}\!\) | \(f_{1111}\!\) | \(1~1~1~1\!\) | \(((~))\!\) | \(\text{true}\!\) | \(1\!\) |
Transforms Expanded over Differential Features
The next four Tables expand the expressions of \(\mathrm{E}f\!\) and \(\mathrm{D}f~\!\) in two different ways, for each of the sixteen functions. Notice that the functions are given in a different order, partitioned into seven natural classes by a group action.
| \(f\!\) |
\(\mathrm{T}_{11} f\!\) \(\mathrm{E}f|_{\mathrm{d}p~\mathrm{d}q}\!\) |
\(\mathrm{T}_{10} f\!\) \(\mathrm{E}f|_{\mathrm{d}p(\mathrm{d}q)}\!\) |
\(\mathrm{T}_{01} f\!\) \(\mathrm{E}f|_{(\mathrm{d}p)\mathrm{d}q}\!\) |
\(\mathrm{T}_{00} f\!\) \(\mathrm{E}f|_{(\mathrm{d}p)(\mathrm{d}q)}\!\) | |
| \(f_0\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) |
|
\(\begin{matrix} f_1 \\[4pt] f_2 \\[4pt] f_4 \\[4pt] f_8 \end{matrix}\!\) |
\(\begin{matrix} (p)(q) \\[4pt] (p)~q~ \\[4pt] ~p~(q) \\[4pt] ~p~~q~ \end{matrix}\!\) |
\(\begin{matrix} ~p~~q~ \\[4pt] ~p~(q) \\[4pt] (p)~q~ \\[4pt] (p)(q) \end{matrix}\!\) |
\(\begin{matrix} ~p~(q) \\[4pt] ~p~~q~ \\[4pt] (p)(q) \\[4pt] (p)~q~ \end{matrix}\!\) |
\(\begin{matrix} (p)~q~ \\[4pt] (p)(q) \\[4pt] ~p~~q~ \\[4pt] ~p~(q) \end{matrix}\!\) |
\(\begin{matrix} (p)(q) \\[4pt] (p)~q~ \\[4pt] ~p~(q) \\[4pt] ~p~~q~ \end{matrix}\!\) |
|
\(\begin{matrix} f_3 \\[4pt] f_{12} \end{matrix}\!\) |
\(\begin{matrix} (p) \\[4pt] ~p~ \end{matrix}\!\) |
\(\begin{matrix} ~p~ \\[4pt] (p) \end{matrix}\!\) |
\(\begin{matrix} ~p~ \\[4pt] (p) \end{matrix}\!\) |
\(\begin{matrix} (p) \\[4pt] ~p~ \end{matrix}\!\) |
\(\begin{matrix} (p) \\[4pt] ~p~ \end{matrix}\!\) |
|
\(\begin{matrix} f_6 \\[4pt] f_9 \end{matrix}\!\) |
\(\begin{matrix} ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
\(\begin{matrix} ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
\(\begin{matrix} ((p,~q)) \\[4pt] ~(p,~q)~ \end{matrix}\!\) |
\(\begin{matrix} ((p,~q)) \\[4pt] ~(p,~q)~ \end{matrix}\!\) |
\(\begin{matrix} ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
|
\(\begin{matrix} f_5 \\[4pt] f_{10} \end{matrix}\!\) |
\(\begin{matrix} (q) \\[4pt] ~q~ \end{matrix}\!\) |
\(\begin{matrix} ~q~ \\[4pt] (q) \end{matrix}\!\) |
\(\begin{matrix} (q) \\[4pt] ~q~ \end{matrix}\!\) |
\(\begin{matrix} ~q~ \\[4pt] (q) \end{matrix}\!\) |
\(\begin{matrix} (q) \\[4pt] ~q~ \end{matrix}\!\) |
|
\(\begin{matrix} f_7 \\[4pt] f_{11} \\[4pt] f_{13} \\[4pt] f_{14} \end{matrix}\!\) |
\(\begin{matrix} (~p~~q~) \\[4pt] (~p~(q)) \\[4pt] ((p)~q~) \\[4pt] ((p)(q)) \end{matrix}\!\) |
\(\begin{matrix} ((p)(q)) \\[4pt] ((p)~q~) \\[4pt] (~p~(q)) \\[4pt] (~p~~q~) \end{matrix}\!\) |
\(\begin{matrix} ((p)~q~) \\[4pt] ((p)(q)) \\[4pt] (~p~~q~) \\[4pt] (~p~(q)) \end{matrix}\!\) |
\(\begin{matrix} (~p~(q)) \\[4pt] (~p~~q~) \\[4pt] ((p)(q)) \\[4pt] ((p)~q~) \end{matrix}\!\) |
\(\begin{matrix} (~p~~q~) \\[4pt] (~p~(q)) \\[4pt] ((p)~q~) \\[4pt] ((p)(q)) \end{matrix}\!\) |
| \(f_{15}\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) |
| \(\text{Fixed Point Total}\!\) | \(4\!\) | \(4\!\) | \(4\!\) | \(16\!\) | |
| \(f\!\) |
\(\mathrm{D}f|_{\mathrm{d}p~\mathrm{d}q}\!\) |
\(\mathrm{D}f|_{\mathrm{d}p(\mathrm{d}q)}\!\) |
\(\mathrm{D}f|_{(\mathrm{d}p)\mathrm{d}q}\!\) |
\(\mathrm{D}f|_{(\mathrm{d}p)(\mathrm{d}q)}\!\) | |
| \(f_0\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) |
|
\(\begin{matrix} f_1 \\[4pt] f_2 \\[4pt] f_4 \\[4pt] f_8 \end{matrix}\!\) |
\(\begin{matrix} (p)(q) \\[4pt] (p)~q~ \\[4pt] ~p~(q) \\[4pt] ~p~~q~ \end{matrix}\!\) |
\(\begin{matrix} ((p,~q)) \\[4pt] ~(p,~q)~ \\[4pt] ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
\(\begin{matrix} (q) \\[4pt] ~q~ \\[4pt] (q) \\[4pt] ~q~ \end{matrix}\!\) |
\(\begin{matrix} (p) \\[4pt] (p) \\[4pt] ~p~ \\[4pt] ~p~ \end{matrix}\!\) |
\(\begin{matrix} (~) \\[4pt] (~) \\[4pt] (~) \\[4pt] (~) \end{matrix}\!\) |
|
\(\begin{matrix} f_3 \\[4pt] f_{12} \end{matrix}\!\) |
\(\begin{matrix} (p) \\[4pt] ~p~ \end{matrix}\!\) |
\(\begin{matrix} ((~)) \\[4pt] ((~)) \end{matrix}~\!\) |
\(\begin{matrix} ((~)) \\[4pt] ((~)) \end{matrix}~\!\) |
\(\begin{matrix} (~) \\[4pt] (~) \end{matrix}\!\) |
\(\begin{matrix} (~) \\[4pt] (~) \end{matrix}\!\) |
|
\(\begin{matrix} f_6 \\[4pt] f_9 \end{matrix}\!\) |
\(\begin{matrix} ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
\(\begin{matrix} (~) \\[4pt] (~) \end{matrix}\!\) |
\(\begin{matrix} ((~)) \\[4pt] ((~)) \end{matrix}~\!\) |
\(\begin{matrix} ((~)) \\[4pt] ((~)) \end{matrix}~\!\) |
\(\begin{matrix} (~) \\[4pt] (~) \end{matrix}\!\) |
|
\(\begin{matrix} f_5 \\[4pt] f_{10} \end{matrix}\!\) |
\(\begin{matrix} (q) \\[4pt] ~q~ \end{matrix}\!\) |
\(\begin{matrix} ((~)) \\[4pt] ((~)) \end{matrix}~\!\) |
\(\begin{matrix} (~) \\[4pt] (~) \end{matrix}\!\) |
\(\begin{matrix} ((~)) \\[4pt] ((~)) \end{matrix}~\!\) |
\(\begin{matrix} (~) \\[4pt] (~) \end{matrix}\!\) |
|
\(\begin{matrix} f_7 \\[4pt] f_{11} \\[4pt] f_{13} \\[4pt] f_{14} \end{matrix}\!\) |
\(\begin{matrix} ~(p~~q)~ \\[4pt] ~(p~(q)) \\[4pt] ((p)~q)~ \\[4pt] ((p)(q)) \end{matrix}\!\) |
\(\begin{matrix} ((p,~q)) \\[4pt] ~(p,~q)~ \\[4pt] ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
\(\begin{matrix} ~q~ \\[4pt] (q) \\[4pt] ~q~ \\[4pt] (q) \end{matrix}\!\) |
\(\begin{matrix} ~p~ \\[4pt] ~p~ \\[4pt] (p) \\[4pt] (p) \end{matrix}\!\) |
\(\begin{matrix} (~) \\[4pt] (~) \\[4pt] (~) \\[4pt] (~) \end{matrix}\!\) |
| \(f_{15}\!\) | \(((~))\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) |
Transforms Expanded over Ordinary Features
| \(f\!\) | \(\mathrm{E}f|_{pq}\!\) | \(\mathrm{E}f|_{p(q)}\!\) | \(\mathrm{E}f|_{(p)q}\!\) | \(\mathrm{E}f|_{(p)(q)}\!\) | |
| \(f_0\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) |
|
\(\begin{matrix} f_1 \\[4pt] f_2 \\[4pt] f_4 \\[4pt] f_8 \end{matrix}\!\) |
\(\begin{matrix} (p)(q) \\[4pt] (p)~q~ \\[4pt] ~p~(q) \\[4pt] ~p~~q~ \end{matrix}\!\) |
\(\begin{matrix} ~\mathrm{d}p~~\mathrm{d}q~ \\[4pt] ~\mathrm{d}p~(\mathrm{d}q) \\[4pt] (\mathrm{d}p)~\mathrm{d}q~ \\[4pt] (\mathrm{d}p)(\mathrm{d}q) \end{matrix}\!\) |
\(\begin{matrix} ~\mathrm{d}p~(\mathrm{d}q) \\[4pt] ~\mathrm{d}p~~\mathrm{d}q~ \\[4pt] (\mathrm{d}p)(\mathrm{d}q) \\[4pt] (\mathrm{d}p)~\mathrm{d}q~ \end{matrix}\!\) |
\(\begin{matrix} (\mathrm{d}p)~\mathrm{d}q~ \\[4pt] (\mathrm{d}p)(\mathrm{d}q) \\[4pt] ~\mathrm{d}p~~\mathrm{d}q~ \\[4pt] ~\mathrm{d}p~(\mathrm{d}q) \end{matrix}\!\) |
\(\begin{matrix} (\mathrm{d}p)(\mathrm{d}q) \\[4pt] (\mathrm{d}p)~\mathrm{d}q~ \\[4pt] ~\mathrm{d}p~(\mathrm{d}q) \\[4pt] ~\mathrm{d}p~~\mathrm{d}q~ \end{matrix}\!\) |
|
\(\begin{matrix} f_3 \\[4pt] f_{12} \end{matrix}\!\) |
\(\begin{matrix} (p) \\[4pt] ~p~ \end{matrix}\!\) |
\(\begin{matrix} ~\mathrm{d}p~ \\[4pt] (\mathrm{d}p) \end{matrix}\!\) |
\(\begin{matrix} ~\mathrm{d}p~ \\[4pt] (\mathrm{d}p) \end{matrix}\!\) |
\(\begin{matrix} (\mathrm{d}p) \\[4pt] ~\mathrm{d}p~ \end{matrix}~\!\) |
\(\begin{matrix} (\mathrm{d}p) \\[4pt] ~\mathrm{d}p~ \end{matrix}~\!\) |
|
\(\begin{matrix} f_6 \\[4pt] f_9 \end{matrix}\!\) |
\(\begin{matrix} ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
\(\begin{matrix} ~(\mathrm{d}p,~\mathrm{d}q)~ \\[4pt] ((\mathrm{d}p,~\mathrm{d}q)) \end{matrix}\!\) |
\(\begin{matrix} ((\mathrm{d}p,~\mathrm{d}q)) \\[4pt] ~(\mathrm{d}p,~\mathrm{d}q)~ \end{matrix}\!\) |
\(\begin{matrix} ((\mathrm{d}p,~\mathrm{d}q)) \\[4pt] ~(\mathrm{d}p,~\mathrm{d}q)~ \end{matrix}\!\) |
\(\begin{matrix} ~(\mathrm{d}p,~\mathrm{d}q)~ \\[4pt] ((\mathrm{d}p,~\mathrm{d}q)) \end{matrix}\!\) |
|
\(\begin{matrix} f_5 \\[4pt] f_{10} \end{matrix}\!\) |
\(\begin{matrix} (q) \\[4pt] ~q~ \end{matrix}\!\) |
\(\begin{matrix} ~\mathrm{d}q~ \\[4pt] (\mathrm{d}q) \end{matrix}\!\) |
\(\begin{matrix} (\mathrm{d}q) \\[4pt] ~\mathrm{d}q~ \end{matrix}\!\) |
\(\begin{matrix} ~\mathrm{d}q~ \\[4pt] (\mathrm{d}q) \end{matrix}\!\) |
\(\begin{matrix} (\mathrm{d}q) \\[4pt] ~\mathrm{d}q~ \end{matrix}\!\) |
|
\(\begin{matrix} f_7 \\[4pt] f_{11} \\[4pt] f_{13} \\[4pt] f_{14} \end{matrix}\!\) |
\(\begin{matrix} (~p~~q~) \\[4pt] (~p~(q)) \\[4pt] ((p)~q~) \\[4pt] ((p)(q)) \end{matrix}\!\) |
\(\begin{matrix} ((\mathrm{d}p)(\mathrm{d}q)) \\[4pt] ((\mathrm{d}p)~\mathrm{d}q~) \\[4pt] (~\mathrm{d}p~(\mathrm{d}q)) \\[4pt] (~\mathrm{d}p~~\mathrm{d}q~) \end{matrix}\!\) |
\(\begin{matrix} ((\mathrm{d}p)~\mathrm{d}q~) \\[4pt] ((\mathrm{d}p)(\mathrm{d}q)) \\[4pt] (~\mathrm{d}p~~\mathrm{d}q~) \\[4pt] (~\mathrm{d}p~(\mathrm{d}q)) \end{matrix}\!\) |
\(\begin{matrix} (~\mathrm{d}p~(\mathrm{d}q)) \\[4pt] (~\mathrm{d}p~~\mathrm{d}q~) \\[4pt] ((\mathrm{d}p)(\mathrm{d}q)) \\[4pt] ((\mathrm{d}p)~\mathrm{d}q~) \end{matrix}\!\) |
\(\begin{matrix} (~\mathrm{d}p~~\mathrm{d}q~) \\[4pt] (~\mathrm{d}p~(\mathrm{d}q)) \\[4pt] ((\mathrm{d}p)~\mathrm{d}q~) \\[4pt] ((\mathrm{d}p)(\mathrm{d}q)) \end{matrix}\!\) |
| \(f_{15}\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) |
| \(f\!\) | \(\mathrm{D}f|_{pq}\!\) | \(\mathrm{D}f|_{p(q)}\!\) | \(\mathrm{D}f|_{(p)q}\!\) | \(\mathrm{D}f|_{(p)(q)}\!\) | |
| \(f_0\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) |
|
\(\begin{matrix} f_1 \\[4pt] f_2 \\[4pt] f_4 \\[4pt] f_8 \end{matrix}\!\) |
\(\begin{matrix} (p)(q) \\[4pt] (p)~q~ \\[4pt] ~p~(q) \\[4pt] ~p~~q~ \end{matrix}\!\) |
\(\begin{matrix} ~~\mathrm{d}p~~\mathrm{d}q~~ \\[4pt] ~~\mathrm{d}p~(\mathrm{d}q)~ \\[4pt] ~(\mathrm{d}p)~\mathrm{d}q~~ \\[4pt] ((\mathrm{d}p)(\mathrm{d}q)) \end{matrix}\!\) |
\(\begin{matrix} ~~\mathrm{d}p~(\mathrm{d}q)~ \\[4pt] ~~\mathrm{d}p~~\mathrm{d}q~~ \\[4pt] ((\mathrm{d}p)(\mathrm{d}q)) \\[4pt] ~(\mathrm{d}p)~\mathrm{d}q~~ \end{matrix}\!\) |
\(\begin{matrix} ~(\mathrm{d}p)~\mathrm{d}q~~ \\[4pt] ((\mathrm{d}p)(\mathrm{d}q)) \\[4pt] ~~\mathrm{d}p~~\mathrm{d}q~~ \\[4pt] ~~\mathrm{d}p~(\mathrm{d}q)~ \end{matrix}\!\) |
\(\begin{matrix} ((\mathrm{d}p)(\mathrm{d}q)) \\[4pt] ~(\mathrm{d}p)~\mathrm{d}q~~ \\[4pt] ~~\mathrm{d}p~(\mathrm{d}q)~ \\[4pt] ~~\mathrm{d}p~~\mathrm{d}q~~ \end{matrix}\!\) |
|
\(\begin{matrix} f_3 \\[4pt] f_{12} \end{matrix}\!\) |
\(\begin{matrix} (p) \\[4pt] ~p~ \end{matrix}\!\) |
\(\begin{matrix} \mathrm{d}p \\[4pt] \mathrm{d}p \end{matrix}\!\) |
\(\begin{matrix} \mathrm{d}p \\[4pt] \mathrm{d}p \end{matrix}\!\) |
\(\begin{matrix} \mathrm{d}p \\[4pt] \mathrm{d}p \end{matrix}\!\) |
\(\begin{matrix} \mathrm{d}p \\[4pt] \mathrm{d}p \end{matrix}\!\) |
|
\(\begin{matrix} f_6 \\[4pt] f_9 \end{matrix}\!\) |
\(\begin{matrix} ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
\(\begin{matrix} (\mathrm{d}p,~\mathrm{d}q) \\[4pt] (\mathrm{d}p,~\mathrm{d}q) \end{matrix}\!\) |
\(\begin{matrix} (\mathrm{d}p,~\mathrm{d}q) \\[4pt] (\mathrm{d}p,~\mathrm{d}q) \end{matrix}\!\) |
\(\begin{matrix} (\mathrm{d}p,~\mathrm{d}q) \\[4pt] (\mathrm{d}p,~\mathrm{d}q) \end{matrix}\!\) |
\(\begin{matrix} (\mathrm{d}p,~\mathrm{d}q) \\[4pt] (\mathrm{d}p,~\mathrm{d}q) \end{matrix}\!\) |
|
\(\begin{matrix} f_5 \\[4pt] f_{10} \end{matrix}\!\) |
\(\begin{matrix} (q) \\[4pt] ~q~ \end{matrix}\!\) |
\(\begin{matrix} \mathrm{d}q \\[4pt] \mathrm{d}q \end{matrix}\!\) |
\(\begin{matrix} \mathrm{d}q \\[4pt] \mathrm{d}q \end{matrix}\!\) |
\(\begin{matrix} \mathrm{d}q \\[4pt] \mathrm{d}q \end{matrix}\!\) |
\(\begin{matrix} \mathrm{d}q \\[4pt] \mathrm{d}q \end{matrix}\!\) |
|
\(\begin{matrix} f_7 \\[4pt] f_{11} \\[4pt] f_{13} \\[4pt] f_{14} \end{matrix}\!\) |
\(\begin{matrix} (~p~~q~) \\[4pt] (~p~(q)) \\[4pt] ((p)~q~) \\[4pt] ((p)(q)) \end{matrix}\!\) |
\(\begin{matrix} ((\mathrm{d}p)(\mathrm{d}q)) \\[4pt] ~(\mathrm{d}p)~\mathrm{d}q~~ \\[4pt] ~~\mathrm{d}p~(\mathrm{d}q)~ \\[4pt] ~~\mathrm{d}p~~\mathrm{d}q~~ \end{matrix}\!\) |
\(\begin{matrix} ~(\mathrm{d}p)~\mathrm{d}q~~ \\[4pt] ((\mathrm{d}p)(\mathrm{d}q)) \\[4pt] ~~\mathrm{d}p~~\mathrm{d}q~~ \\[4pt] ~~\mathrm{d}p~(\mathrm{d}q)~ \end{matrix}\!\) |
\(\begin{matrix} ~~\mathrm{d}p~(\mathrm{d}q)~ \\[4pt] ~~\mathrm{d}p~~\mathrm{d}q~~ \\[4pt] ((\mathrm{d}p)(\mathrm{d}q)) \\[4pt] ~(\mathrm{d}p)~\mathrm{d}q~~ \end{matrix}\!\) |
\(\begin{matrix} ~~\mathrm{d}p~~\mathrm{d}q~~ \\[4pt] ~~\mathrm{d}p~(\mathrm{d}q)~ \\[4pt] ~(\mathrm{d}p)~\mathrm{d}q~~ \\[4pt] ((\mathrm{d}p)(\mathrm{d}q)) \end{matrix}\!\) |
| \(f_{15}\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) |
Operational Representation
If you think that I linger in the realm of logical difference calculus out of sheer vacillation about getting down to the differential proper, it is probably out of a prior expectation that you derive from the art or the long-engrained practice of real analysis. But the fact is that ordinary calculus only rushes on to the sundry orders of approximation because the strain of comprehending the full import of \(\mathrm{E}\!\) and \(\mathrm{D}\!\) at once overwhelms its discrete and finite powers to grasp them. But here, in the fully serene idylls of zeroth order logic, we find ourselves fit with the compass of a wit that is all we'd ever need to explore their effects with care.
So let us do just that.
I will first rationalize the novel grouping of propositional forms in the last set of Tables, as that will extend a gentle invitation to the mathematical subject of group theory, and demonstrate its relevance to differential logic in a strikingly apt and useful way. The data for that account is contained in Table A3.
| \(f\!\) |
\(\mathrm{T}_{11} f\!\) \(\mathrm{E}f|_{\mathrm{d}p~\mathrm{d}q}\!\) |
\(\mathrm{T}_{10} f\!\) \(\mathrm{E}f|_{\mathrm{d}p(\mathrm{d}q)}\!\) |
\(\mathrm{T}_{01} f\!\) \(\mathrm{E}f|_{(\mathrm{d}p)\mathrm{d}q}\!\) |
\(\mathrm{T}_{00} f\!\) \(\mathrm{E}f|_{(\mathrm{d}p)(\mathrm{d}q)}\!\) | |
| \(f_0\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) |
|
\(\begin{matrix} f_1 \\[4pt] f_2 \\[4pt] f_4 \\[4pt] f_8 \end{matrix}\!\) |
\(\begin{matrix} (p)(q) \\[4pt] (p)~q~ \\[4pt] ~p~(q) \\[4pt] ~p~~q~ \end{matrix}\!\) |
\(\begin{matrix} ~p~~q~ \\[4pt] ~p~(q) \\[4pt] (p)~q~ \\[4pt] (p)(q) \end{matrix}\!\) |
\(\begin{matrix} ~p~(q) \\[4pt] ~p~~q~ \\[4pt] (p)(q) \\[4pt] (p)~q~ \end{matrix}\!\) |
\(\begin{matrix} (p)~q~ \\[4pt] (p)(q) \\[4pt] ~p~~q~ \\[4pt] ~p~(q) \end{matrix}\!\) |
\(\begin{matrix} (p)(q) \\[4pt] (p)~q~ \\[4pt] ~p~(q) \\[4pt] ~p~~q~ \end{matrix}\!\) |
|
\(\begin{matrix} f_3 \\[4pt] f_{12} \end{matrix}\!\) |
\(\begin{matrix} (p) \\[4pt] ~p~ \end{matrix}\!\) |
\(\begin{matrix} ~p~ \\[4pt] (p) \end{matrix}\!\) |
\(\begin{matrix} ~p~ \\[4pt] (p) \end{matrix}\!\) |
\(\begin{matrix} (p) \\[4pt] ~p~ \end{matrix}\!\) |
\(\begin{matrix} (p) \\[4pt] ~p~ \end{matrix}\!\) |
|
\(\begin{matrix} f_6 \\[4pt] f_9 \end{matrix}\!\) |
\(\begin{matrix} ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
\(\begin{matrix} ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
\(\begin{matrix} ((p,~q)) \\[4pt] ~(p,~q)~ \end{matrix}\!\) |
\(\begin{matrix} ((p,~q)) \\[4pt] ~(p,~q)~ \end{matrix}\!\) |
\(\begin{matrix} ~(p,~q)~ \\[4pt] ((p,~q)) \end{matrix}\!\) |
|
\(\begin{matrix} f_5 \\[4pt] f_{10} \end{matrix}\!\) |
\(\begin{matrix} (q) \\[4pt] ~q~ \end{matrix}\!\) |
\(\begin{matrix} ~q~ \\[4pt] (q) \end{matrix}\!\) |
\(\begin{matrix} (q) \\[4pt] ~q~ \end{matrix}\!\) |
\(\begin{matrix} ~q~ \\[4pt] (q) \end{matrix}\!\) |
\(\begin{matrix} (q) \\[4pt] ~q~ \end{matrix}\!\) |
|
\(\begin{matrix} f_7 \\[4pt] f_{11} \\[4pt] f_{13} \\[4pt] f_{14} \end{matrix}\!\) |
\(\begin{matrix} (~p~~q~) \\[4pt] (~p~(q)) \\[4pt] ((p)~q~) \\[4pt] ((p)(q)) \end{matrix}\!\) |
\(\begin{matrix} ((p)(q)) \\[4pt] ((p)~q~) \\[4pt] (~p~(q)) \\[4pt] (~p~~q~) \end{matrix}\!\) |
\(\begin{matrix} ((p)~q~) \\[4pt] ((p)(q)) \\[4pt] (~p~~q~) \\[4pt] (~p~(q)) \end{matrix}\!\) |
\(\begin{matrix} (~p~(q)) \\[4pt] (~p~~q~) \\[4pt] ((p)(q)) \\[4pt] ((p)~q~) \end{matrix}\!\) |
\(\begin{matrix} (~p~~q~) \\[4pt] (~p~(q)) \\[4pt] ((p)~q~) \\[4pt] ((p)(q)) \end{matrix}\!\) |
| \(f_{15}\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) |
| \(\text{Fixed Point Total}\!\) | \(4\!\) | \(4\!\) | \(4\!\) | \(16\!\) | |
The shift operator \(\mathrm{E}\!\) can be understood as enacting a substitution operation on the propositional form \(f(p, q)\!\) that is given as its argument. In our present focus on propositional forms that involve two variables, we have the following type specifications and definitions:
|
\(\begin{array}{lcl} \mathrm{E} ~:~ (X \to \mathbb{B}) & \to & (\mathrm{E}X \to \mathbb{B}) \\[6pt] \mathrm{E} ~:~ f(p, q) & \mapsto & \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) \\[6pt] \mathrm{E}f(p, q, \mathrm{d}p, \mathrm{d}q) & = & f(p + \mathrm{d}p, q + \mathrm{d}q) \\[6pt] & = & f( \texttt{(} p, \mathrm{d}p \texttt{)}, \texttt{(} q, \mathrm{d}q \texttt{)} ) \end{array}\!\) |
Evaluating \(\mathrm{E}f\!\) at particular values of \(\mathrm{d}p\!\) and \(\mathrm{d}q,\!\) for example, \(\mathrm{d}p = i\!\) and \(\mathrm{d}q = j,\!\) where \(i\!\) and \(j\!\) are values in \(\mathbb{B},\!\) produces the following result:
|
\(\begin{array}{lclcl} \mathrm{E}_{ij} & : & (X \to \mathbb{B}) & \to & (X \to \mathbb{B}) \\[6pt] \mathrm{E}_{ij} & : & f & \mapsto & \mathrm{E}_{ij}f \\[6pt] \mathrm{E}_{ij}f & = & \mathrm{E}f|_{\mathrm{d}p = i, \mathrm{d}q = j} & = & f(p + i, q + j) \\[6pt] & & & = & f( \texttt{(} p, i \texttt{)}, \texttt{(} q, j \texttt{)} ) \end{array}\!\) |
The notation is a little awkward, but the data of Table A3 should make the sense clear. The important thing to observe is that \(\mathrm{E}_{ij}\!\) has the effect of transforming each proposition \(f : X \to \mathbb{B}\!\) into a proposition \(f^\prime : X \to \mathbb{B}.\!\) As it happens, the action of each \(\mathrm{E}_{ij}\!\) is one-to-one and onto, so the gang of four operators \(\{ \mathrm{E}_{ij} : i, j \in \mathbb{B} \}\!\) is an example of what is called a transformation group on the set of sixteen propositions. Bowing to a longstanding local and linear tradition, I will therefore redub the four elements of this group as \(\mathrm{T}_{00}, \mathrm{T}_{01}, \mathrm{T}_{10}, \mathrm{T}_{11},\!\) to bear in mind their transformative character, or nature, as the case may be. Abstractly viewed, this group of order four has the following operation table:
|
\(\cdot\!\) |
\(\mathrm{T}_{00}\!\) |
\(\mathrm{T}_{01}\!\) |
\(\mathrm{T}_{10}\!\) |
\(\mathrm{T}_{11}\!\) |
| \(\mathrm{T}_{00}\!\) | \(\mathrm{T}_{00}\!\) | \(\mathrm{T}_{01}\!\) | \(\mathrm{T}_{10}\!\) | \(\mathrm{T}_{11}\!\) |
| \(\mathrm{T}_{01}\!\) | \(\mathrm{T}_{01}\!\) | \(\mathrm{T}_{00}\!\) | \(\mathrm{T}_{11}\!\) | \(\mathrm{T}_{10}\!\) |
| \(\mathrm{T}_{10}\!\) | \(\mathrm{T}_{10}\!\) | \(\mathrm{T}_{11}\!\) | \(\mathrm{T}_{00}\!\) | \(\mathrm{T}_{01}\!\) |
| \(\mathrm{T}_{11}\!\) | \(\mathrm{T}_{11}\!\) | \(\mathrm{T}_{10}\!\) | \(\mathrm{T}_{01}\!\) | \(\mathrm{T}_{00}\!\) |
It happens that there are just two possible groups of 4 elements. One is the cyclic group \(Z_4\!\) (from German Zyklus), which this is not. The other is the Klein four-group \(V_4\!\) (from German Vier), which this is.
More concretely viewed, the group as a whole pushes the set of sixteen propositions around in such a way that they fall into seven natural classes, called orbits. One says that the orbits are preserved by the action of the group. There is an Orbit Lemma of immense utility to “those who count” which, depending on your upbringing, you may associate with the names of Burnside, Cauchy, Frobenius, or some subset or superset of these three, vouching that the number of orbits is equal to the mean number of fixed points, in other words, the total number of points (in our case, propositions) that are left unmoved by the separate operations, divided by the order of the group. In this instance, \(\mathrm{T}_{00}\!\) operates as the group identity, fixing all 16 propositions, while the other three group elements fix 4 propositions each, and so we get: Number of Orbits = (4 + 4 + 4 + 16) ÷ 4 = 7. Amazing!
|
Consider what effects that might conceivably have practical bearings you conceive the objects of your conception to have. Then, your conception of those effects is the whole of your conception of the object. |
| — Charles Sanders Peirce, “Issues of Pragmaticism”, (CP 5.438) |
One other subject that it would be opportune to mention at this point, while we have an object example of a mathematical group fresh in mind, is the relationship between the pragmatic maxim and what are commonly known in mathematics as representation principles. As it turns out, with regard to its formal characteristics, the pragmatic maxim unites the aspects of a representation principle with the attributes of what would ordinarily be known as a closure principle. We will consider the form of closure that is invoked by the pragmatic maxim on another occasion, focusing here and now on the topic of group representations.
Let us return to the example of the four-group \(V_4.\!\) We encountered this group in one of its concrete representations, namely, as a transformation group that acts on a set of objects, in this case a set of sixteen functions or propositions. Forgetting about the set of objects that the group transforms among themselves, we may take the abstract view of the group's operational structure, for example, in the form of the group operation table copied here:
|
\(\cdot\!\) |
\(\mathrm{e}\!\) |
\(\mathrm{f}\!\) |
\(\mathrm{g}\!\) |
\(\mathrm{h}\!\) |
| \(\mathrm{e}\!\) | \(\mathrm{e}\!\) | \(\mathrm{f}\!\) | \(\mathrm{g}\!\) | \(\mathrm{h}\!\) |
| \(\mathrm{f}\!\) | \(\mathrm{f}\!\) | \(\mathrm{e}\!\) | \(\mathrm{h}\!\) | \(\mathrm{g}\!\) |
| \(\mathrm{g}\!\) | \(\mathrm{g}\!\) | \(\mathrm{h}\!\) | \(\mathrm{e}\!\) | \(\mathrm{f}\!\) |
| \(\mathrm{h}\!\) | \(\mathrm{h}\!\) | \(\mathrm{g}\!\) | \(\mathrm{f}\!\) | \(\mathrm{e}\!\) |
This table is abstractly the same as, or isomorphic to, the versions with the \(\mathrm{E}_{ij}\!\) operators and the \(\mathrm{T}_{ij}\!\) transformations that we took up earlier. That is to say, the story is the same, only the names have been changed. An abstract group can have a variety of significantly and superficially different representations. But even after we have long forgotten the details of any particular representation there is a type of concrete representations, called regular representations, that are always readily available, as they can be generated from the mere data of the abstract operation table itself.
To see how a regular representation is constructed from the abstract operation table, select a group element from the top margin of the Table, and “consider its effects” on each of the group elements as they are listed along the left margin. We may record these effects as Peirce usually did, as a logical aggregate of elementary dyadic relatives, that is, as a logical disjunction or boolean sum whose terms represent the ordered pairs of \(\mathrm{input} : \mathrm{output}\!\) transactions that are produced by each group element in turn. This forms one of the two possible regular representations of the group, in this case the one that is called the post-regular representation or the right regular representation. It has long been conventional to organize the terms of this logical aggregate in the form of a matrix:
Reading “\(+\!\)” as a logical disjunction:
|
\(\begin{matrix} \mathrm{G} & = & \mathrm{e} & + & \mathrm{f} & + & \mathrm{g} & + & \mathrm{h} \end{matrix}\!\) |
And so, by expanding effects, we get:
|
\(\begin{matrix} \mathrm{G} & = & \mathrm{e}:\mathrm{e} & + & \mathrm{f}:\mathrm{f} & + & \mathrm{g}:\mathrm{g} & + & \mathrm{h}:\mathrm{h} \\[4pt] & + & \mathrm{e}:\mathrm{f} & + & \mathrm{f}:\mathrm{e} & + & \mathrm{g}:\mathrm{h} & + & \mathrm{h}:\mathrm{g} \\[4pt] & + & \mathrm{e}:\mathrm{g} & + & \mathrm{f}:\mathrm{h} & + & \mathrm{g}:\mathrm{e} & + & \mathrm{h}:\mathrm{f} \\[4pt] & + & \mathrm{e}:\mathrm{h} & + & \mathrm{f}:\mathrm{g} & + & \mathrm{g}:\mathrm{f} & + & \mathrm{h}:\mathrm{e} \end{matrix}\!\) |
More on the pragmatic maxim as a representation principle later.
The above-mentioned fact about the regular representations of a group is universally known as Cayley's Theorem, typically stated in the following form:
| Every group is isomorphic to a subgroup of \(\mathrm{Aut}(X),\!\) the group of automorphisms of a suitably chosen set \(X\!\). |
There is a considerable generalization of these regular representations to a broad class of relational algebraic systems in Peirce's earliest papers. The crux of the whole idea is this:
| Contemplate the effects of the symbol whose meaning you wish to investigate as they play out on all the stages of conduct where you can imagine that symbol playing a role. |
This idea of contextual definition by way of conduct transforming operators is basically the same as Jeremy Bentham's notion of paraphrasis, a “method of accounting for fictions by explaining various purported terms away” (Quine, in Van Heijenoort, From Frege to Gödel, p. 216). Today we'd call these constructions term models. This, again, is the big idea behind Schönfinkel's combinators \(\mathrm{S}, \mathrm{K}, \mathrm{I},\!\) and hence of lambda calculus, and I reckon you know where that leads.
The next few excursions in this series will provide a scenic tour of various ideas in group theory that will turn out to be of constant guidance in several of the settings that are associated with our topic.
Let me return to Peirce's early papers on the algebra of relatives to pick up the conventions that he used there, and then rewrite my account of regular representations in a way that conforms to those.
Peirce describes the action of an “elementary dual relative” in this way:
| Elementary simple relatives are connected together in systems of four. For if \(\mathrm{A}\!:\!\mathrm{B}\!\) be taken to denote the elementary relative which multiplied into \(\mathrm{B}\!\) gives \(\mathrm{A},\!\) then this relation existing as elementary, we have the four elementary relatives |
| \(\mathrm{A}\!:\!\mathrm{A} \qquad \mathrm{A}\!:\!\mathrm{B} \qquad \mathrm{B}\!:\!\mathrm{A} \qquad \mathrm{B}\!:\!\mathrm{B}.\!\) |
| C.S. Peirce, Collected Papers, CP 3.123. |
Peirce is well aware that it is not at all necessary to arrange the elementary relatives of a relation into arrays, matrices, or tables, but when he does so he tends to prefer organizing 2-adic relations in the following manner:
|
\(\begin{bmatrix} a\!:\!a & a\!:\!b & a\!:\!c \\ b\!:\!a & b\!:\!b & b\!:\!c \\ c\!:\!a & c\!:\!b & c\!:\!c \end{bmatrix}\!\) |
For example, given the set \(X = \{ a, b, c \},\!\) suppose that we have the 2-adic relative term \(\mathit{m} = {}^{\backprime\backprime}\, \text{marker for}\, \underline{~ ~ ~}\, {}^{\prime\prime}~\!\) and the associated 2-adic relation \(M \subseteq X \times X,\!\) the general pattern of whose common structure is represented by the following matrix:
|
\( M \quad = \quad \begin{bmatrix} M_{aa}(a\!:\!a) & M_{ab}(a\!:\!b) & M_{ac}(a\!:\!c) \\ M_{ba}(b\!:\!a) & M_{bb}(b\!:\!b) & M_{bc}(b\!:\!c) \\ M_{ca}(c\!:\!a) & M_{cb}(c\!:\!b) & M_{cc}(c\!:\!c) \end{bmatrix} \!\) |
For at least a little while longer, I will keep explicit the distinction between a relative term like \(\mathit{m}\!\) and a relation like \(M \subseteq X \times X,\!\) but it is best to view both these entities as involving different applications of the same information, and so we could just as easily write the following form:
|
\( m \quad = \quad \begin{bmatrix} m_{aa}(a\!:\!a) & m_{ab}(a\!:\!b) & m_{ac}(a\!:\!c) \\ m_{ba}(b\!:\!a) & m_{bb}(b\!:\!b) & m_{bc}(b\!:\!c) \\ m_{ca}(c\!:\!a) & m_{cb}(c\!:\!b) & m_{cc}(c\!:\!c) \end{bmatrix} \!\) |
By way of making up a concrete example, let us say that \(\mathit{m}\!\) or \(M\!\) is given as follows:
|
\(\begin{array}{l} a ~\text{is a marker for}~ a \\ a ~\text{is a marker for}~ b \\ b ~\text{is a marker for}~ b \\ b ~\text{is a marker for}~ c \\ c ~\text{is a marker for}~ c \\ c ~\text{is a marker for}~ a \end{array}\!\) |
In sum, then, the relative term \(\mathit{m}\!\) and the relation \(M\!\) are both represented by the following matrix:
|
\(\begin{bmatrix} 1 \cdot (a\!:\!a) & 1 \cdot (a\!:\!b) & 0 \cdot (a\!:\!c) \\ 0 \cdot (b\!:\!a) & 1 \cdot (b\!:\!b) & 1 \cdot (b\!:\!c) \\ 1 \cdot (c\!:\!a) & 0 \cdot (c\!:\!b) & 1 \cdot (c\!:\!c) \end{bmatrix}\!\) |
I think this much will serve to fix notation and set up the remainder of the discussion.
In Peirce's time, and even in some circles of mathematics today, the information indicated by the elementary relatives \((i\!:\!j),\!\) as the indices \(i, j\!\) range over the universe of discourse, would be referred to as the umbral elements of the algebraic operation represented by the matrix, though I seem to recall that Peirce preferred to call these terms the “ingredients”. When this ordered basis is understood well enough, one will tend to drop any mention of it from the matrix itself, leaving us nothing but these bare bones:
|
\( M \quad = \quad \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{bmatrix} \!\) |
The various representations of \(M\!\) are nothing more than alternative ways of specifying its basic ingredients, namely, the following aggregate of elementary relatives:
|
\(\begin{array}{*{13}{c}} M & = & a\!:\!a & + & b\!:\!b & + & c\!:\!c & + & a\!:\!b & + & b\!:\!c & + & c\!:\!a \end{array}\!\) |
Recognizing that \(a\!:\!a + b\!:\!b + c\!:\!c\!\) is the identity transformation otherwise known as \(\mathit{1},\!\) the 2-adic relative term \(m = {}^{\backprime\backprime}\, \text{marker for}\, \underline{~ ~ ~}\, {}^{\prime\prime}~\!\) can be parsed as an element \(\mathit{1} + a\!:\!b + b\!:\!c + c\!:\!a\!\) of the so-called group ring, all of which makes this element just a special sort of linear transformation.
Up to this point, we are still reading the elementary relatives of the form \(i\!:\!j\!\) in the way that Peirce read them in logical contexts: \(i\!\) is the relate, \(j\!\) is the correlate, and in our current example \(i\!:\!j,\!\) or more exactly, \(m_{ij} = 1,\!\) is taken to say that \(i\!\) is a marker for \(j.\!\) This is the mode of reading that we call “multiplying on the left”.
In the algebraic, permutational, or transformational contexts of application, however, Peirce converts to the alternative mode of reading, although still calling \(i\!\) the relate and \(j\!\) the correlate, the elementary relative \(i\!:\!j\!\) now means that \(i\!\) gets changed into \(j.\!\) In this scheme of reading, the transformation \(a\!:\!b + b\!:\!c + c\!:\!a\!\) is a permutation of the aggregate \(\mathbf{1} = a + b + c,\!\) or what we would now call the set \(\{ a, b, c \},\!\) in particular, it is the permutation that is otherwise notated as follows:
|
\(\begin{Bmatrix} a & b & c \\ b & c & a \end{Bmatrix}\!\) |
This is consistent with the convention that Peirce uses in the paper “On a Class of Multiple Algebras” (CP 3.324–327).
We've been exploring the applications of a certain technique for clarifying abstruse concepts, a rough-cut version of the pragmatic maxim that I've been accustomed to refer to as the operationalization of ideas. The basic idea is to replace the question of What it is, which modest people comprehend is far beyond their powers to answer definitively any time soon, with the question of What it does, which most people know at least a modicum about.
In the case of regular representations of groups we found a non-plussing surplus of answers to sort our way through. So let us track back one more time to see if we can learn any lessons that might carry over to more realistic cases.
Here is is the operation table of \(V_4\!\) once again:
|
\(\cdot\!\) |
\(\mathrm{e}\!\) |
\(\mathrm{f}\!\) |
\(\mathrm{g}\!\) |
\(\mathrm{h}\!\) |
| \(\mathrm{e}\!\) | \(\mathrm{e}\!\) | \(\mathrm{f}\!\) | \(\mathrm{g}\!\) | \(\mathrm{h}\!\) |
| \(\mathrm{f}\!\) | \(\mathrm{f}\!\) | \(\mathrm{e}\!\) | \(\mathrm{h}\!\) | \(\mathrm{g}\!\) |
| \(\mathrm{g}\!\) | \(\mathrm{g}\!\) | \(\mathrm{h}\!\) | \(\mathrm{e}\!\) | \(\mathrm{f}\!\) |
| \(\mathrm{h}\!\) | \(\mathrm{h}\!\) | \(\mathrm{g}\!\) | \(\mathrm{f}\!\) | \(\mathrm{e}\!\) |
A group operation table is really just a device for recording a certain 3-adic relation, to be specific, the set of triples of the form \((x, y, z)\!\) satisfying the equation \(x \cdot y = z.\!\)
In the case of \(V_4 = (G, \cdot),\!\) where \(G\!\) is the underlying set \(\{ \mathrm{e}, \mathrm{f}, \mathrm{g}, \mathrm{h} \},\!\) we have the 3-adic relation \(L(V_4) \subseteq G \times G \times G\!\) whose triples are listed below:
|
\(\begin{matrix} (\mathrm{e}, \mathrm{e}, \mathrm{e}) & (\mathrm{e}, \mathrm{f}, \mathrm{f}) & (\mathrm{e}, \mathrm{g}, \mathrm{g}) & (\mathrm{e}, \mathrm{h}, \mathrm{h}) \\[6pt] (\mathrm{f}, \mathrm{e}, \mathrm{f}) & (\mathrm{f}, \mathrm{f}, \mathrm{e}) & (\mathrm{f}, \mathrm{g}, \mathrm{h}) & (\mathrm{f}, \mathrm{h}, \mathrm{g}) \\[6pt] (\mathrm{g}, \mathrm{e}, \mathrm{g}) & (\mathrm{g}, \mathrm{f}, \mathrm{h}) & (\mathrm{g}, \mathrm{g}, \mathrm{e}) & (\mathrm{g}, \mathrm{h}, \mathrm{f}) \\[6pt] (\mathrm{h}, \mathrm{e}, \mathrm{h}) & (\mathrm{h}, \mathrm{f}, \mathrm{g}) & (\mathrm{h}, \mathrm{g}, \mathrm{f}) & (\mathrm{h}, \mathrm{h}, \mathrm{e}) \end{matrix}\!\) |
It is part of the definition of a group that the 3-adic relation \(L \subseteq G^3\!\) is actually a function \(L : G \times G \to G.\!\) It is from this functional perspective that we can see an easy way to derive the two regular representations. Since we have a function of the type \(L : G \times G \to G,\!\) we can define a couple of substitution operators:
| 1. | \(\mathrm{Sub}(x, (\underline{~~}, y))\!\) puts any specified \(x\!\) into the empty slot of the rheme \((\underline{~~}, y),\!\) with the effect of producing the saturated rheme \((x, y)\!\) that evaluates to \(xy.~\!\) |
| 2. | \(\mathrm{Sub}(x, (y, \underline{~~}))\!\) puts any specified \(x\!\) into the empty slot of the rheme \((y, \underline{~~}),\!\) with the effect of producing the saturated rheme \((y, x)\!\) that evaluates to \(yx.~\!\) |
In (1) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((\underline{~~}, y),\!\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((\underline{~~}, y)\!\) into \(xy,\!\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : xy) ~|~ y \in G \}.\!\) The pairs \((y : xy)\!\) can be found by picking an \(x\!\) from the left margin of the group operation table and considering its effects on each \(y\!\) in turn as these run across the top margin. This aspect of pragmatic definition we recognize as the regular ante-representation:
|
\(\begin{matrix} \mathrm{e} & = & \mathrm{e}\!:\!\mathrm{e} & + & \mathrm{f}\!:\!\mathrm{f} & + & \mathrm{g}\!:\!\mathrm{g} & + & \mathrm{h}\!:\!\mathrm{h} \\[4pt] \mathrm{f} & = & \mathrm{e}\!:\!\mathrm{f} & + & \mathrm{f}\!:\!\mathrm{e} & + & \mathrm{g}\!:\!\mathrm{h} & + & \mathrm{h}\!:\!\mathrm{g} \\[4pt] \mathrm{g} & = & \mathrm{e}\!:\!\mathrm{g} & + & \mathrm{f}\!:\!\mathrm{h} & + & \mathrm{g}\!:\!\mathrm{e} & + & \mathrm{h}\!:\!\mathrm{f} \\[4pt] \mathrm{h} & = & \mathrm{e}\!:\!\mathrm{h} & + & \mathrm{f}\!:\!\mathrm{g} & + & \mathrm{g}\!:\!\mathrm{f} & + & \mathrm{h}\!:\!\mathrm{e} \end{matrix}\!\) |
In (2) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((y, \underline{~~}),\!\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((y, \underline{~~})\!\) into \(yx,\!\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : yx) ~|~ y \in G \}.\!\) The pairs \((y : yx)\!\) can be found by picking an \(x\!\) from the top margin of the group operation table and considering its effects on each \(y\!\) in turn as these run down the left margin. This aspect of pragmatic definition we recognize as the regular post-representation:
|
\(\begin{matrix} \mathrm{e} & = & \mathrm{e}\!:\!\mathrm{e} & + & \mathrm{f}\!:\!\mathrm{f} & + & \mathrm{g}\!:\!\mathrm{g} & + & \mathrm{h}\!:\!\mathrm{h} \\[4pt] \mathrm{f} & = & \mathrm{e}\!:\!\mathrm{f} & + & \mathrm{f}\!:\!\mathrm{e} & + & \mathrm{g}\!:\!\mathrm{h} & + & \mathrm{h}\!:\!\mathrm{g} \\[4pt] \mathrm{g} & = & \mathrm{e}\!:\!\mathrm{g} & + & \mathrm{f}\!:\!\mathrm{h} & + & \mathrm{g}\!:\!\mathrm{e} & + & \mathrm{h}\!:\!\mathrm{f} \\[4pt] \mathrm{h} & = & \mathrm{e}\!:\!\mathrm{h} & + & \mathrm{f}\!:\!\mathrm{g} & + & \mathrm{g}\!:\!\mathrm{f} & + & \mathrm{h}\!:\!\mathrm{e} \end{matrix}\!\) |
If the ante-rep looks the same as the post-rep, now that I'm writing them in the same dialect, that is because \(V_4\!\) is abelian (commutative), and so the two representations have the very same effects on each point of their bearing.
So long as we're in the neighborhood, we might as well take in some more of the sights, for instance, the smallest example of a non-abelian (non-commutative) group. This is a group of six elements, say, \(G = \{ \mathrm{e}, \mathrm{f}, \mathrm{g}, \mathrm{h}, \mathrm{i}, \mathrm{j} \},\!\) with no relation to any other employment of these six symbols being implied, of course, and it can be most easily represented as the permutation group on a set of three letters, say, \(X = \{ a, b, c \},\!\) usually notated as \(G = \mathrm{Sym}(X)\!\) or more abstractly and briefly, as \(\mathrm{Sym}(3)\!\) or \(S_3.\!\) The next Table shows the intended correspondence between abstract group elements and the permutation or substitution operations in \(\mathrm{Sym}(X).\!\)
| \(\mathrm{e}\!\) | \(\mathrm{f}\!\) | \(\mathrm{g}\!\) | \(\mathrm{h}\!\) | \(\mathrm{i}~\!\) | \(\mathrm{j}\!\) |
|
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] a & b & c \end{matrix}\!\) |
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] c & a & b \end{matrix}\!\) |
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] b & c & a \end{matrix}\!\) |
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] a & c & b \end{matrix}\!\) |
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] c & b & a \end{matrix}\!\) |
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] b & a & c \end{matrix}\!\) |
Here is the operation table for \(S_3,\!\) given in abstract fashion:
| \(\text{Symmetric Group}~ S_3\!\) |
|
By the way, we will meet with the symmetric group \(S_3~\!\) again when we return to take up the study of Peirce's early paper “On a Class of Multiple Algebras” (CP 3.324–327), and also his late unpublished work “The Simplest Mathematics” (1902) (CP 4.227–323), with particular reference to the section that treats of “Trichotomic Mathematics” (CP 4.307–323).
By way of collecting a short-term pay-off for all the work that we did on the regular representations of the Klein 4-group \(V_4,\!\) let us write out as quickly as possible in relative form a minimal budget of representations for the symmetric group on three letters, \(\mathrm{Sym}(3).\!\) After doing the usual bit of compare and contrast among the various representations, we will have enough concrete material beneath our abstract belts to tackle a few of the presently obscured details of Peirce's early “Algebra + Logic” papers.
Writing the permutations or substitutions of \(\mathrm{Sym} \{ a, b, c \}\!\) in relative form generates what is generally thought of as a natural representation of \(S_3.~\!\)
|
\(\begin{matrix} \mathrm{e} & = & a\!:\!a & + & b\!:\!b & + & c\!:\!c \\[4pt] \mathrm{f} & = & a\!:\!c & + & b\!:\!a & + & c\!:\!b \\[4pt] \mathrm{g} & = & a\!:\!b & + & b\!:\!c & + & c\!:\!a \\[4pt] \mathrm{h} & = & a\!:\!a & + & b\!:\!c & + & c\!:\!b \\[4pt] \mathrm{i} & = & a\!:\!c & + & b\!:\!b & + & c\!:\!a \\[4pt] \mathrm{j} & = & a\!:\!b & + & b\!:\!a & + & c\!:\!c \end{matrix}\!\) |
I have without stopping to think about it written out this natural representation of \(S_3~\!\) in the style that comes most naturally to me, to wit, the “right” way, whereby an ordered pair configured as \(x\!:\!y\!\) constitutes the turning of \(x\!\) into \(y.\!\) It is possible that the next time we check in with CSP we will have to adjust our sense of direction, but that will be an easy enough bridge to cross when we come to it.
To construct the regular representations of \(S_3,~\!\) we begin with the data of its operation table:
| \(\text{Symmetric Group}~ S_3\!\) |

|
Just by way of staying clear about what we are doing, let's return to the recipe that we worked out before:
It is part of the definition of a group that the 3-adic relation \(L \subseteq G^3\!\) is actually a function \(L : G \times G \to G.\!\) It is from this functional perspective that we can see an easy way to derive the two regular representations.
Since we have a function of the type \(L : G \times G \to G,\!\) we can define a couple of substitution operators:
| 1. | \(\mathrm{Sub}(x, (\underline{~~}, y))\!\) puts any specified \(x\!\) into the empty slot of the rheme \((\underline{~~}, y),\!\) with the effect of producing the saturated rheme \((x, y)\!\) that evaluates to \(xy.~\!\) |
| 2. | \(\mathrm{Sub}(x, (y, \underline{~~}))\!\) puts any specified \(x\!\) into the empty slot of the rheme \((y, \underline{~~}),\!\) with the effect of producing the saturated rheme \((y, x)\!\) that evaluates to \(yx.~\!\) |
In (1) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((\underline{~~}, y),\!\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((\underline{~~}, y)\!\) into \(xy,\!\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : xy) ~|~ y \in G \}.\!\) The pairs \((y : xy)\!\) can be found by picking an \(x\!\) from the left margin of the group operation table and considering its effects on each \(y\!\) in turn as these run along the right margin. This produces the regular ante-representation of \(S_3,\!\) like so:
|
\(\begin{array}{*{13}{c}} \mathrm{e} & = & \mathrm{e}\!:\!\mathrm{e} & + & \mathrm{f}\!:\!\mathrm{f} & + & \mathrm{g}\!:\!\mathrm{g} & + & \mathrm{h}\!:\!\mathrm{h} & + & \mathrm{i}\!:\!\mathrm{i} & + & \mathrm{j}\!:\!\mathrm{j} \\[4pt] \mathrm{f} & = & \mathrm{e}\!:\!\mathrm{f} & + & \mathrm{f}\!:\!\mathrm{g} & + & \mathrm{g}\!:\!\mathrm{e} & + & \mathrm{h}\!:\!\mathrm{j} & + & \mathrm{i}\!:\!\mathrm{h} & + & \mathrm{j}\!:\!\mathrm{i} \\[4pt] \mathrm{g} & = & \mathrm{e}\!:\!\mathrm{g} & + & \mathrm{f}\!:\!\mathrm{e} & + & \mathrm{g}\!:\!\mathrm{f} & + & \mathrm{h}\!:\!\mathrm{i} & + & \mathrm{i}\!:\!\mathrm{j} & + & \mathrm{j}\!:\!\mathrm{h} \\[4pt] \mathrm{h} & = & \mathrm{e}\!:\!\mathrm{h} & + & \mathrm{f}\!:\!\mathrm{i} & + & \mathrm{g}\!:\!\mathrm{j} & + & \mathrm{h}\!:\!\mathrm{e} & + & \mathrm{i}\!:\!\mathrm{f} & + & \mathrm{j}\!:\!\mathrm{g} \\[4pt] \mathrm{i} & = & \mathrm{e}\!:\!\mathrm{i} & + & \mathrm{f}\!:\!\mathrm{j} & + & \mathrm{g}\!:\!\mathrm{h} & + & \mathrm{h}\!:\!\mathrm{g} & + & \mathrm{i}\!:\!\mathrm{e} & + & \mathrm{j}\!:\!\mathrm{f} \\[4pt] \mathrm{j} & = & \mathrm{e}\!:\!\mathrm{j} & + & \mathrm{f}\!:\!\mathrm{h} & + & \mathrm{g}\!:\!\mathrm{i} & + & \mathrm{h}\!:\!\mathrm{f} & + & \mathrm{i}\!:\!\mathrm{g} & + & \mathrm{j}\!:\!\mathrm{e} \end{array}\!\) |
In (2) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((y, \underline{~~}),\!\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((y, \underline{~~})\!\) into \(yx,\!\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : yx) ~|~ y \in G \}.\!\) The pairs \((y : yx)\!\) can be found by picking an \(x\!\) on the right margin of the group operation table and considering its effects on each \(y\!\) in turn as these run along the left margin. This produces the regular post-representation of \(S_3,\!\) like so:
|
\(\begin{array}{*{13}{c}} \mathrm{e} & = & \mathrm{e}\!:\!\mathrm{e} & + & \mathrm{f}\!:\!\mathrm{f} & + & \mathrm{g}\!:\!\mathrm{g} & + & \mathrm{h}\!:\!\mathrm{h} & + & \mathrm{i}\!:\!\mathrm{i} & + & \mathrm{j}\!:\!\mathrm{j} \\[4pt] \mathrm{f} & = & \mathrm{e}\!:\!\mathrm{f} & + & \mathrm{f}\!:\!\mathrm{g} & + & \mathrm{g}\!:\!\mathrm{e} & + & \mathrm{h}\!:\!\mathrm{i} & + & \mathrm{i}\!:\!\mathrm{j} & + & \mathrm{j}\!:\!\mathrm{h} \\[4pt] \mathrm{g} & = & \mathrm{e}\!:\!\mathrm{g} & + & \mathrm{f}\!:\!\mathrm{e} & + & \mathrm{g}\!:\!\mathrm{f} & + & \mathrm{h}\!:\!\mathrm{j} & + & \mathrm{i}\!:\!\mathrm{h} & + & \mathrm{j}\!:\!\mathrm{i} \\[4pt] \mathrm{h} & = & \mathrm{e}\!:\!\mathrm{h} & + & \mathrm{f}\!:\!\mathrm{j} & + & \mathrm{g}\!:\!\mathrm{i} & + & \mathrm{h}\!:\!\mathrm{e} & + & \mathrm{i}\!:\!\mathrm{g} & + & \mathrm{j}\!:\!\mathrm{f} \\[4pt] \mathrm{i} & = & \mathrm{e}\!:\!\mathrm{i} & + & \mathrm{f}\!:\!\mathrm{h} & + & \mathrm{g}\!:\!\mathrm{j} & + & \mathrm{h}\!:\!\mathrm{f} & + & \mathrm{i}\!:\!\mathrm{e} & + & \mathrm{j}\!:\!\mathrm{g} \\[4pt] \mathrm{j} & = & \mathrm{e}\!:\!\mathrm{j} & + & \mathrm{f}\!:\!\mathrm{i} & + & \mathrm{g}\!:\!\mathrm{h} & + & \mathrm{h}\!:\!\mathrm{g} & + & \mathrm{i}\!:\!\mathrm{f} & + & \mathrm{j}\!:\!\mathrm{e} \end{array}\!\) |
If the ante-rep looks different from the post-rep, it is just as it should be, as \(S_3~\!\) is non-abelian (non-commutative), and so the two representations differ in the details of their practical effects, though, of course, being representations of the same abstract group, they must be isomorphic.
|
the way of heaven and earth | |
| — i ching, hexagram 32 |
The Reader may be wondering what happened to the announced subject of Dynamics And Logic. What happened was a bit like this:
We made the observation that the shift operators \(\{ \mathrm{E}_{ij} \}\!\) form a transformation group that acts on the set of propositions of the form \(f : \mathbb{B} \times \mathbb{B} \to \mathbb{B}.\!\) Group theory is a very attractive subject, but it did not draw us so far from our intended course as one might initially think. For one thing, groups, especially the groups that are named after the Norwegian mathematician Marius Sophus Lie (1842–1899), have turned out to be of critical utility in the solution of differential equations. For another thing, group operations provide us with an ample supply of triadic relations that have been extremely well-studied over the years, and thus they give us no small measure of useful guidance in the study of sign relations, another brand of 3-adic relations that have significance for logical studies, and in our acquaintance with which we have barely begun to break the ice. Finally, I couldn't resist taking up the links between group representations, amounting to the very archetypes of logical models, and the pragmatic maxim.
We've seen a couple of groups, \(V_4\!\) and \(S_3,\!\) represented in various ways, and we've seen their representations presented in a variety of different manners. Let us look at one other stylistic variant for presenting a representation that is frequently seen, the so-called matrix representation of a group.
Recalling the manner of our acquaintance with the symmetric group \(S_3,\!\) we began with the bigraph (bipartite graph) picture of its natural representation as the set of all permutations or substitutions on the set \(X = \{ a, b, c \}.\!\)
| \(\mathrm{e}\!\) | \(\mathrm{f}\!\) | \(\mathrm{g}\!\) | \(\mathrm{h}\!\) | \(\mathrm{i}~\!\) | \(\mathrm{j}\!\) |
|
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] a & b & c \end{matrix}\!\) |
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] c & a & b \end{matrix}\!\) |
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] b & c & a \end{matrix}\!\) |
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] a & c & b \end{matrix}\!\) |
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] c & b & a \end{matrix}\!\) |
\(\begin{matrix} a & b & c \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] b & a & c \end{matrix}\!\) |
These permutations were then converted to relative form as logical sums of elementary relatives:
|
\(\begin{matrix} \mathrm{e} & = & a\!:\!a & + & b\!:\!b & + & c\!:\!c \\[4pt] \mathrm{f} & = & a\!:\!c & + & b\!:\!a & + & c\!:\!b \\[4pt] \mathrm{g} & = & a\!:\!b & + & b\!:\!c & + & c\!:\!a \\[4pt] \mathrm{h} & = & a\!:\!a & + & b\!:\!c & + & c\!:\!b \\[4pt] \mathrm{i} & = & a\!:\!c & + & b\!:\!b & + & c\!:\!a \\[4pt] \mathrm{j} & = & a\!:\!b & + & b\!:\!a & + & c\!:\!c \end{matrix}\!\) |
From the relational representation of \(\mathrm{Sym} \{ a, b, c \} \cong S_3,\!\) one easily derives a linear representation of the group by viewing each permutation as a linear transformation that maps the elements of a suitable vector space onto each other. Each of these linear transformations is in turn represented by a 2-dimensional array of coefficients in \(\mathbb{B},\!\) resulting in the following set of matrices for the group:
| \(\mathrm{e}\!\) | \(\mathrm{f}\!\) | \(\mathrm{g}\!\) | \(\mathrm{h}\!\) | \(\mathrm{i}~\!\) | \(\mathrm{j}\!\) |
|
\(\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}~\!\) |
\(\begin{matrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{matrix}~\!\) |
\(\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{matrix}\!\) |
\(\begin{matrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{matrix}~\!\) |
\(\begin{matrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{matrix}~\!\) |
\(\begin{matrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{matrix}~\!\) |
The key to the mysteries of these matrices is revealed by observing that their coefficient entries are arrayed and overlaid on a place-mat marked like so:
|
\(\begin{bmatrix} a\!:\!a & a\!:\!b & a\!:\!c \\ b\!:\!a & b\!:\!b & b\!:\!c \\ c\!:\!a & c\!:\!b & c\!:\!c \end{bmatrix}\!\) |
Quick Review : Field Picture
Let us summarize, in rough but intuitive terms, the outlook on differential logic that we have reached so far. We've been considering a class of operators on universes of discourse, each of which takes us from considering one universe of discourse, \(X^\circ,\!\) to considering a larger universe of discourse, \(\mathrm{E}X^\circ.\!\) An operator \(\mathrm{W}\!\) of this general type, namely, \(\mathrm{W} : X^\circ \to \mathrm{E}X^\circ,\!\) acts on each proposition \(f : X \to \mathbb{B}\!\) of the source universe \({X^\circ}\!\) to produce a proposition \(\mathrm{W}f : \mathrm{E}X \to \mathbb{B}\!\) of the target universe \(\mathrm{E}X^\circ.\!\)
The two main operators that we've examined so far are the enlargement or shift operator \(\mathrm{E} : X^\circ \to \mathrm{E}X^\circ\!\) and the difference operator \(\mathrm{D} : X^\circ \to \mathrm{E}X^\circ.\!\) The operators \(\mathrm{E}\!\) and \(\mathrm{D}\!\) act on propositions in \(X^\circ,\!\) that is, propositions of the form \(f : X \to \mathbb{B}\!\) that are said to be about the subject matter of \(X,\!\) and they produce extended propositions of the forms \(\mathrm{E}f, \mathrm{D}f : \mathrm{E}X \to \mathbb{B},\!\) propositions whose extended sets of variables allow them to be read as being about specified collections of changes that conceivably occur in \(X.\!\)
At this point we find ourselves in need of visual representations, suitable arrays of concrete pictures to anchor our more earthy intuitions and to help us keep our wits about us as we venture higher into the ever more rarefied air of abstractions.
One good picture comes to us by way of the field concept. Given a space \(X,\!\) a field of a specified type \(Y\!\) over \(X\!\) is formed by associating with each point of \(X\!\) an object of type \(Y.\!\) If that sounds like the same thing as a function from \(X\!\) to the space of things of type \(Y\!\) — it is nothing but — and yet it does seem helpful to vary the mental images and to take advantage of the figures of speech that spring to mind under the emblem of this field idea.
In the field picture a proposition \(f : X \to \mathbb{B}\!\) becomes a scalar field, that is, a field of values in \(\mathbb{B}.\!\)
For example, consider the logical conjunction \(pq : X \to \mathbb{B}\!\) that is shown in the following venn diagram:
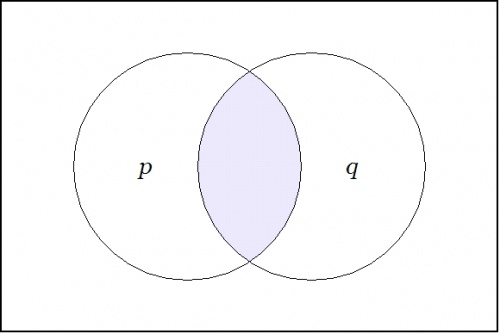
|
| \(\text{Conjunction}~ pq : X \to \mathbb{B}\!\) |
Each of the operators \(\mathrm{E}, \mathrm{D} : X^\circ \to \mathrm{E}X^\circ\!\) takes us from considering propositions \(f : X \to \mathbb{B},\!\) here viewed as scalar fields over \(X,\!\) to considering the corresponding differential fields over \(X,\!\) analogous to what are usually called vector fields over \(X.\!\)
The structure of these differential fields can be described this way. With each point of \(X\!\) there is associated an object of the following type: a proposition about changes in \(X,\!\) that is, a proposition \(g : \mathrm{d}X \to \mathbb{B}.\!\) In this frame of reference, if \({X^\circ}\!\) is the universe that is generated by the set of coordinate propositions \(\{ p, q \},\!\) then \(\mathrm{d}X^\circ\!\) is the differential universe that is generated by the set of differential propositions \(\{ \mathrm{d}p, \mathrm{d}q \}.\!\) These differential propositions may be interpreted as indicating \({}^{\backprime\backprime} \text{change in}\, p \, {}^{\prime\prime}\!\) and \({}^{\backprime\backprime} \text{change in}\, q \, {}^{\prime\prime},\!\) respectively.
A differential operator \(\mathrm{W},\!\) of the first order class that we have been considering, takes a proposition \(f : X \to \mathbb{B}\!\) and gives back a differential proposition \(\mathrm{W}f : \mathrm{E}X \to \mathbb{B}.\!\) In the field view, we see the proposition \(f : X \to \mathbb{B}\!\) as a scalar field and we see the differential proposition \(\mathrm{W}f : \mathrm{E}X \to \mathbb{B}\!\) as a vector field, specifically, a field of propositions about contemplated changes in \(X.\!\)
The field of changes produced by \(\mathrm{E}\!\) on \(pq\!\) is shown in the next venn diagram:
The differential field \(\mathrm{E}(pq)\!\) specifies the changes that need to be made from each point of \(X\!\) in order to reach one of the models of the proposition \(pq,\!\) that is, in order to satisfy the proposition \(pq.\!\)
The field of changes produced by \(\mathrm{D}\!\) on \(pq\!\) is shown in the following venn diagram:
The differential field \(\mathrm{D}(pq)\!\) specifies the changes that need to be made from each point of \(X\!\) in order to feel a change in the felt value of the field \(pq.\!\)
Proposition and Tacit Extension
Now that we've introduced the field picture as an aid to thinking about propositions and their analytic series, a very pleasing way of picturing the relationships among a proposition \(f : X \to \mathbb{B},\!\) its enlargement or shift map \(\mathrm{E}f : \mathrm{E}X \to \mathbb{B},\!\) and its difference map \(\mathrm{D}f : \mathrm{E}X \to \mathbb{B}\!\) can now be drawn.
To illustrate this possibility, let's return to the differential analysis of the conjunctive proposition \(f(p, q) = pq,\!\) giving the development a slightly different twist at the appropriate point.
The next venn diagram shows once again the proposition \(pq,\!\) which we now view as a scalar field — analogous to a potential hill in physics, but in logic tantamount to a potential plateau — where the shaded region indicates an elevation of 1 and the unshaded region indicates an elevation of 0.

|
| \(\text{Proposition}~ pq : X \to \mathbb{B}\!\) |
Given a proposition \(f : X \to \mathbb{B},\!\) the tacit extension of \(f\!\) to \(\mathrm{E}X\!\) is denoted \(\boldsymbol\varepsilon f : \mathrm{E}X \to \mathbb{B}~\!\) and defined by the equation \(\boldsymbol\varepsilon f = f,\!\) so it's really just the same proposition residing in a bigger universe. Tacit extensions formalize the intuitive idea that a function on a particular set of variables can be extended to a function on a superset of those variables in such a way that the new function obeys the same constraints on the old variables, with a "don't care" condition on the new variables.
The tacit extension of the scalar field \(pq : X \to \mathbb{B}\!\) to the differential field \(\boldsymbol\varepsilon (pq) : \mathrm{E}X \to \mathbb{B}\!\) is shown in the following venn diagram:
Enlargement and Difference Maps
Continuing with the example \(pq : X \to \mathbb{B},\!\) the next venn diagram shows the enlargement or shift map \(\mathrm{E}(pq) : \mathrm{E}X \to \mathbb{B}\!\) in the same style of differential field picture that we drew for the tacit extension \(\boldsymbol\varepsilon (pq) : \mathrm{E}X \to \mathbb{B}.\!\)
A very important conceptual transition has just occurred here, almost tacitly, as it were. Generally speaking, having a set of mathematical objects of compatible types, in this case the two differential fields \(\boldsymbol\varepsilon f\!\) and \(\mathrm{E}f,\!\) both of the type \(\mathrm{E}X \to \mathbb{B},\!\) is very useful, because it allows us to consider these fields as integral mathematical objects that can be operated on and combined in the ways that we usually associate with algebras.
In this case one notices that the tacit extension \(\boldsymbol\varepsilon f\!\) and the enlargement \(\mathrm{E}f\!\) are in a certain sense dual to each other. The tacit extension \(\boldsymbol\varepsilon f\!\) indicates all the arrows out of the region where \(f\!\) is true and the enlargement \(\mathrm{E}f\!\) indicates all the arrows into the region where \(f\!\) is true. The only arc they have in common is the no-change loop \(\texttt{(} \mathrm{d}p \texttt{)(} \mathrm{d}q \texttt{)}\!\) at \(pq.\!\) If we add the two sets of arcs in mod 2 fashion then the loop of multiplicity 2 zeroes out, leaving the 6 arrows of \(\mathrm{D}(pq) = \boldsymbol\varepsilon(pq) + \mathrm{E}(pq)\!\) that are illustrated below:
Tangent and Remainder Maps
If we follow the classical line that singles out linear functions as ideals of simplicity, then we may complete the analytic series of the proposition \(f = pq : X \to \mathbb{B}\!\) in the following way.
The next venn diagram shows the differential proposition \(\mathrm{d}f = \mathrm{d}(pq) : \mathrm{E}X \to \mathbb{B}\!\) that we get by extracting the cell-wise linear approximation to the difference map \(\mathrm{D}f = \mathrm{D}(pq) : \mathrm{E}X \to \mathbb{B}.\!\) This is the logical analogue of what would ordinarily be called the differential of \(pq,\!\) but since I've been attaching the adjective differential to just about everything in sight, the distinction tends to be lost. For the time being, I'll resort to using the alternative name tangent map for \(\mathrm{d}f.\!\)
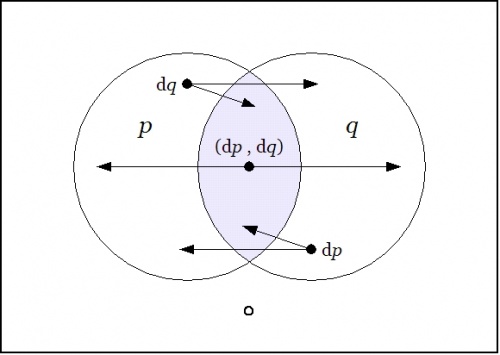
|
| \(\text{Tangent Map}~ \mathrm{d}(pq) : \mathrm{E}X \to \mathbb{B}\!\) |
Just to be clear about what's being indicated here, it's a visual way of summarizing the following data:
|
\(\begin{array}{rcccccc} \mathrm{d}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \mathrm{d}p \texttt{,} \mathrm{d}q \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \mathrm{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \mathrm{d}p \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & 0 \end{array}\!\) |
To understand the extended interpretations, that is, the conjunctions of basic and differential features that are being indicated here, it may help to note the following equivalences:
|
\(\begin{matrix} \texttt{(} \mathrm{d}p \texttt{,} \mathrm{d}q \texttt{)} & = & \texttt{~} \mathrm{d}p \texttt{~} \texttt{(} \mathrm{d}q \texttt{)} & + & \texttt{(} \mathrm{d}p \texttt{)} \texttt{~} \mathrm{d}q \texttt{~} \\[4pt] dp & = & \texttt{~} \mathrm{d}p \texttt{~} \texttt{~} \mathrm{d}q \texttt{~} & + & \texttt{~} \mathrm{d}p \texttt{~} \texttt{(} \mathrm{d}q \texttt{)} \\[4pt] \mathrm{d}q & = & \texttt{~} \mathrm{d}p \texttt{~} \texttt{~} \mathrm{d}q \texttt{~} & + & \texttt{(} \mathrm{d}p \texttt{)} \texttt{~} \mathrm{d}q \texttt{~} \end{matrix}\!\) |
Capping the series that analyzes the proposition \(pq\!\) in terms of succeeding orders of linear propositions, the final venn diagram in this series shows the remainder map \(\mathrm{r}(pq) : \mathrm{E}X \to \mathbb{B},\!\) that happens to be linear in pairs of variables.
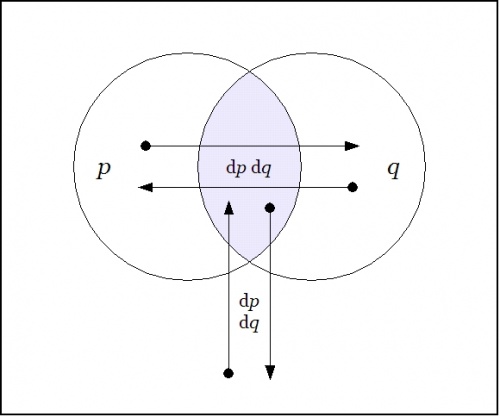
|
| \(\text{Remainder Map}~ \mathrm{r}(pq) : \mathrm{E}X \to \mathbb{B}\!\) |
Reading the arrows off the map produces the following data:
|
\(\begin{array}{rcccccc} \mathrm{r}(pq) & = & p & \cdot & q & \cdot & \mathrm{d}p ~ \mathrm{d}q \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \mathrm{d}p ~ \mathrm{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \mathrm{d}p ~ \mathrm{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & \mathrm{d}p ~ \mathrm{d}q \end{array}\!\) |
In short, \(\mathrm{r}(pq)\!\) is a constant field, having the value \(\mathrm{d}p~\mathrm{d}q\!\) at each cell.
Least Action Operators
We have been contemplating functions of the type \(f : X \to \mathbb{B}\!\) and studying the action of the operators \(\mathrm{E}\!\) and \(\mathrm{D}\!\) on this family. These functions, that we may identify for our present aims with propositions, inasmuch as they capture their abstract forms, are logical analogues of scalar potential fields. These are the sorts of fields that are so picturesquely presented in elementary calculus and physics textbooks by images of snow-covered hills and parties of skiers who trek down their slopes like least action heroes. The analogous scene in propositional logic presents us with forms more reminiscent of plateaunic idylls, being all plains at one of two levels, the mesas of verity and falsity, as it were, with nary a niche to inhabit between them, restricting our options for a sporting gradient of downhill dynamics to just one of two: standing still on level ground or falling off a bluff.
We are still working well within the logical analogue of the classical finite difference calculus, taking in the novelties that the logical transmutation of familiar elements is able to bring to light. Soon we will take up several different notions of approximation relationships that may be seen to organize the space of propositions, and these will allow us to define several different forms of differential analysis applying to propositions. In time we will find reason to consider more general types of maps, having concrete types of the form \(X_1 \times \ldots \times X_k \to Y_1 \times \ldots \times Y_n\!\) and abstract types \(\mathbb{B}^k \to \mathbb{B}^n.\!\) We will think of these mappings as transforming universes of discourse into themselves or into others, in short, as transformations of discourse.
Before we continue with this intinerary, however, I would like to highlight another sort of differential aspect that concerns the boundary operator or the marked connective that serves as one of the two basic connectives in the cactus language for zeroth order logic.
For example, consider the proposition \(f\!\) of concrete type \(f : P \times Q \times R \to \mathbb{B}\!\) and abstract type \(f : \mathbb{B}^3 \to \mathbb{B}\!\) that is written \(\texttt{(} p, q, r \texttt{)}\!\) in cactus syntax. Taken as an assertion in what Peirce called the existential interpretation, the proposition \(\texttt{(} p, q, r \texttt{)}\!\) says that just one of \(p, q, r\!\) is false. It is instructive to consider this assertion in relation to the logical conjunction \(pqr\!\) of the same propositions. A venn diagram of \(\texttt{(} p, q, r \texttt{)}\!\) looks like this:
|
In relation to the center cell indicated by the conjunction \(pqr,\!\) the region indicated by \(\texttt{(} p, q, r \texttt{)}\!\) is comprised of the adjacent or bordering cells. Thus they are the cells that are just across the boundary of the center cell, reached as if by way of Leibniz's minimal changes from the point of origin, in this case, \(pqr.~\!\)
More generally speaking, in a \(k\!\)-dimensional universe of discourse that is based on the alphabet of features \(\mathcal{X} = \{ x_1, \ldots, x_k \},\!\) the same form of boundary relationship is manifested for any cell of origin that one chooses to indicate. One way to indicate a cell is by forming a logical conjunction of positive and negative basis features, that is, by constructing an expression of the form \(e_1 \cdot \ldots \cdot e_k,\!\) where \(e_j = x_j ~\text{or}~ e_j = \texttt{(} x_j \texttt{)},\!\) for \(j = 1 ~\text{to}~ k.\!\) The proposition \(\texttt{(} e_1, \ldots, e_k \texttt{)}\!\) indicates the disjunctive region consisting of the cells that are just next door to \(e_1 \cdot \ldots \cdot e_k.\!\)
Goal-Oriented Systems
I want to continue developing the basic tools of differential logic, which arose from exploring the connections between dynamics and logic, but I also wanted to give some hint of the applications that have motivated this work all along. One of these applications is to cybernetic systems, whether we see these systems as agents or cultures, individuals or species, organisms or organizations.
A cybernetic system has goals and actions for reaching them. It has a state space \(X,\!\) giving us all of the states that the system can be in, plus it has a goal space \(G \subseteq X,\!\) the set of states that the system “likes” to be in, in other words, the distinguished subset of possible states where the system is regarded as living, surviving, or thriving, depending on the type of goal that one has in mind for the system in question. As for actions, there is to begin with the full set \(\mathcal{T}\!\) of all possible actions, each of which is a transformation of the form \(T : X \to X,\!\) but a given cybernetic system will most likely have but a subset of these actions available to it at any given time. And even if we begin by thinking of actions in very general and very global terms, as arbitrarily complex transformations acting on the whole state space \(X,\!\) we quickly find a need to analyze and approximate them in terms of simple transformations acting locally. The preferred measure of “simplicity” will of course vary from one paradigm of research to another.
A generic enough picture at this stage of the game, and one that will remind us of these fundamental features of the cybernetic system even as things get far more complex, is afforded by Figure 23.
o---------------------------------------------------------------------o | | | X | | o-------------------o | | / \ | | / \ | | / \ | | / \ | | / \ | | / \ | | / \ | | o G o | | | | | | | | | | | | | | | o<---------T---------o | | | | | | | | | | | | | | o o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | o-------------------o | | | | | o---------------------------------------------------------------------o Figure 23. Elements of a Cybernetic System |
Further Reading
A more detailed presentation of Differential Logic can be found here:
Document History
Differential Logic • Ontology List 2002
- http://web.archive.org/web/20140406040004/http://suo.ieee.org/ontology/msg04040.html
- http://web.archive.org/web/20110612001949/http://suo.ieee.org/ontology/msg04041.html
- http://web.archive.org/web/20110612010502/http://suo.ieee.org/ontology/msg04045.html
- http://web.archive.org/web/20110612005212/http://suo.ieee.org/ontology/msg04046.html
- http://web.archive.org/web/20110612001954/http://suo.ieee.org/ontology/msg04047.html
- http://web.archive.org/web/20110612010620/http://suo.ieee.org/ontology/msg04048.html
- http://web.archive.org/web/20110612010550/http://suo.ieee.org/ontology/msg04052.html
- http://web.archive.org/web/20110612010724/http://suo.ieee.org/ontology/msg04054.html
- http://web.archive.org/web/20110612000847/http://suo.ieee.org/ontology/msg04055.html
- http://web.archive.org/web/20110612001959/http://suo.ieee.org/ontology/msg04067.html
- http://web.archive.org/web/20110612010507/http://suo.ieee.org/ontology/msg04068.html
- http://web.archive.org/web/20110612002014/http://suo.ieee.org/ontology/msg04069.html
- http://web.archive.org/web/20110612010701/http://suo.ieee.org/ontology/msg04070.html
- http://web.archive.org/web/20110612003540/http://suo.ieee.org/ontology/msg04072.html
- http://web.archive.org/web/20110612005229/http://suo.ieee.org/ontology/msg04073.html
- http://web.archive.org/web/20110610153117/http://suo.ieee.org/ontology/msg04074.html
- http://web.archive.org/web/20110612010555/http://suo.ieee.org/ontology/msg04077.html
- http://web.archive.org/web/20110612001918/http://suo.ieee.org/ontology/msg04079.html
- http://web.archive.org/web/20110612005244/http://suo.ieee.org/ontology/msg04080.html
- http://web.archive.org/web/20110612005249/http://suo.ieee.org/ontology/msg04268.html
- http://web.archive.org/web/20110612010626/http://suo.ieee.org/ontology/msg04269.html
- http://web.archive.org/web/20110612000853/http://suo.ieee.org/ontology/msg04272.html
- http://web.archive.org/web/20110612010514/http://suo.ieee.org/ontology/msg04273.html
- http://web.archive.org/web/20110612002235/http://suo.ieee.org/ontology/msg04290.html
Dynamics And Logic • Inquiry List 2004
- http://stderr.org/pipermail/inquiry/2004-May/thread.html#1400
- http://stderr.org/pipermail/inquiry/2004-July/thread.html#1685
- http://stderr.org/pipermail/inquiry/2004-May/001400.html
- http://stderr.org/pipermail/inquiry/2004-May/001401.html
- http://stderr.org/pipermail/inquiry/2004-May/001402.html
- http://stderr.org/pipermail/inquiry/2004-May/001403.html
- http://stderr.org/pipermail/inquiry/2004-May/001404.html
- http://stderr.org/pipermail/inquiry/2004-May/001405.html
- http://stderr.org/pipermail/inquiry/2004-May/001406.html
- http://stderr.org/pipermail/inquiry/2004-May/001407.html
- http://stderr.org/pipermail/inquiry/2004-May/001408.html
- http://stderr.org/pipermail/inquiry/2004-May/001410.html
- http://stderr.org/pipermail/inquiry/2004-May/001411.html
- http://stderr.org/pipermail/inquiry/2004-May/001412.html
- http://stderr.org/pipermail/inquiry/2004-May/001413.html
- http://stderr.org/pipermail/inquiry/2004-May/001415.html
- http://stderr.org/pipermail/inquiry/2004-May/001416.html
- http://stderr.org/pipermail/inquiry/2004-May/001418.html
- http://stderr.org/pipermail/inquiry/2004-May/001419.html
- http://stderr.org/pipermail/inquiry/2004-May/001420.html
- http://stderr.org/pipermail/inquiry/2004-May/001421.html
- http://stderr.org/pipermail/inquiry/2004-May/001422.html
- http://stderr.org/pipermail/inquiry/2004-May/001423.html
- http://stderr.org/pipermail/inquiry/2004-May/001424.html
- http://stderr.org/pipermail/inquiry/2004-July/001685.html
- http://stderr.org/pipermail/inquiry/2004-July/001686.html
- http://stderr.org/pipermail/inquiry/2004-July/001687.html
- http://stderr.org/pipermail/inquiry/2004-July/001688.html
Dynamics And Logic • NKS Forum 2004
- http://forum.wolframscience.com/archive/topic/420.html
- http://forum.wolframscience.com/printthread.php?threadid=420
- http://forum.wolframscience.com/showthread.php?threadid=420
- http://forum.wolframscience.com/showthread.php?postid=1282#post1282
- http://forum.wolframscience.com/showthread.php?postid=1285#post1285
- http://forum.wolframscience.com/showthread.php?postid=1289#post1289
- http://forum.wolframscience.com/showthread.php?postid=1292#post1292
- http://forum.wolframscience.com/showthread.php?postid=1293#post1293
- http://forum.wolframscience.com/showthread.php?postid=1294#post1294
- http://forum.wolframscience.com/showthread.php?postid=1296#post1296
- http://forum.wolframscience.com/showthread.php?postid=1299#post1299
- http://forum.wolframscience.com/showthread.php?postid=1301#post1301
- http://forum.wolframscience.com/showthread.php?postid=1304#post1304
- http://forum.wolframscience.com/showthread.php?postid=1307#post1307
- http://forum.wolframscience.com/showthread.php?postid=1309#post1309
- http://forum.wolframscience.com/showthread.php?postid=1311#post1311
- http://forum.wolframscience.com/showthread.php?postid=1314#post1314
- http://forum.wolframscience.com/showthread.php?postid=1315#post1315
- http://forum.wolframscience.com/showthread.php?postid=1318#post1318
- http://forum.wolframscience.com/showthread.php?postid=1321#post1321
- http://forum.wolframscience.com/showthread.php?postid=1323#post1323
- http://forum.wolframscience.com/showthread.php?postid=1326#post1326
- http://forum.wolframscience.com/showthread.php?postid=1327#post1327
- http://forum.wolframscience.com/showthread.php?postid=1330#post1330
- http://forum.wolframscience.com/showthread.php?postid=1331#post1331
- http://forum.wolframscience.com/showthread.php?postid=1598#post1598
- http://forum.wolframscience.com/showthread.php?postid=1601#post1601
- http://forum.wolframscience.com/showthread.php?postid=1602#post1602
- http://forum.wolframscience.com/showthread.php?postid=1603#post1603
Notes & Queries
Jon Awbrey 10:54, 10 October 2007 (PDT)
Place For Discussion
Commentary Work Area
Commentary Note 12.2
a b c d e f g h i o o o o o o o o o X | | : | : | | | 0 1 0 1 W, | | : | : | o o o o + - + + o X \ | / : : | | \ | / 0 0 1 1 L \|/ : : | | o o o o o o o o o X a b c d e f g h i |
a b c d e f g h i o o o o o o o o o X / \ : | : | / \ 0 1 0 1 L / \ : | : | o o o o + - + + o X \ | / : : | | \ | / 0 0 1 1 S \|/ : : | | o o o o o o o o o X a b c d e f g h i |
Commentary Note 12.3
a b c d e f g h i
o o o o o o o o o X
| |
| | W,
| |
o o o o o o o o o X
\ \ / / \ | / \ \ / /
\ / / \ | / \ \ / L
\ / \ / \|/ \ / \ /
o o o o o o o o o X
a b c d e f g h i
|
Commentary Note 12.4
|
\(\begin{array}{*{15}{c}} X & = & \{ & a, & b, & c, & d, & e, & f, & g, & h, & i\ & \} \\[6pt] W & = & \{ & d, & f\ & \} \\[6pt] L & = & \{ & b\!:\!a, & b\!:\!c, & c\!:\!b, & c\!:\!d, & e\!:\!d, & e\!:\!e, & e\!:\!f, & g\!:\!f, & g\!:\!h, & h\!:\!g, & h\!:\!i & \} \\[6pt] S & = & \{ & b\!:\!a, & b\!:\!c, & d\!:\!c, & d\!:\!d, & d\!:\!e, & f\!:\!e, & f\!:\!f, & f\!:\!g, & h\!:\!g, & h\!:\!i\ & \} \end{array}\) |
a b c d e f g h i
o o o o o o o o o X
| |
| | W,
| |
o o o o o o o o o X
\ \ / / \ | / \ \ / /
\ / / \ | / \ \ / L
\ / \ / \|/ \ / \ /
o o o o o o o o o X
\ / \ | / \ | / \ /
\ / \ | / \ | / \ / S
\ / \|/ \|/ \ /
o o o o o o o o o X
a b c d e f g h i
|
a b c d e f g h i
o o o o o o o o o X
|
| (LW),
|
o o o o o o o o o X
\ / \ | / \ | / \ /
\ / \ | / \ | / \ / S
\ / \|/ \|/ \ /
o o o o o o o o o X
a b c d e f g h i
|
a b c d e f g h i
o o o o o o o o o X
| |
| | (S^(LW)),
| |
o o o o o o o o o X
a b c d e f g h i
|
a b c d e f g h i o o o o o o o o o X \ \ / / \ | / \ \ / / \ / / \ | / \ \ / L \ / \ / \|/ \ / \ / o o o o o o o o o X \ / \ | / \ | / \ / \ / \ | / \ | / \ / S \ / \|/ \|/ \ / o o o o o o o o o X a b c d e f g h i |
Commentary Note 12.5
|
\( (\mathfrak{L} \mathfrak{W})_x ~=~ \sum_{p \in X} \mathfrak{L}_{xp} \mathfrak{W}_p \) |
|
\( (\mathfrak{L} \mathfrak{W})_q ~=~ \sum_{p \in X} \mathfrak{L}_{qp} \mathfrak{W}_p \) |
|
\((\mathfrak{L}^\mathfrak{W})_x ~=~ \prod_{p \in X} \mathfrak{L}_{xp}^{\mathfrak{W}_p} \) |
|
\( (\mathfrak{S}^\mathfrak{L})_{xy} ~=~ \prod_{p \in X} \mathfrak{S}_{xp}^{\mathfrak{L}_{py}} \) |
|
\( (\mathfrak{S}^\mathfrak{L})_{xp} ~=~ \prod_{q \in X} \mathfrak{S}_{xq}^{\mathfrak{L}_{qp}} \) |
|
\( ((\mathfrak{S}^\mathfrak{L})^\mathfrak{W})_x ~=~ (\mathfrak{S}^{\mathfrak{L}\mathfrak{W}})_x \) |
|
\( ((\mathfrak{S}^\mathfrak{L})^\mathfrak{W})_x ~=~ \prod_{p \in X} (\mathfrak{S}^\mathfrak{L})_{xp}^{\mathfrak{W}_p} ~=~ \prod_{p \in X} (\prod_{q \in X} \mathfrak{S}_{xq}^{\mathfrak{L}_{qp}})^{\mathfrak{W}_p} ~=~ \prod_{p \in X} \prod_{q \in X} \mathfrak{S}_{xq}^{\mathfrak{L}_{qp}\mathfrak{W}_p} \) |
|
\( (\mathfrak{S}^{\mathfrak{L}\mathfrak{W}})_x ~=~ \prod_{q \in X} \mathfrak{S}_{xq}^{(\mathfrak{L}\mathfrak{W})_q} ~=~ \prod_{q \in X} \mathfrak{S}_{xq}^{\sum_{p \in X} \mathfrak{L}_{qp} \mathfrak{W}_p} ~=~ \prod_{q \in X} \prod_{p \in X} \mathfrak{S}_{xq}^{\mathfrak{L}_{qp} \mathfrak{W}_p} \) |
Commentary Note 12.6
Need a comment about the meaning of the sum \(\sum_{p \in X} \mathfrak{L}_{qp} \mathfrak{W}_p\) in the following equation:
|
\( (\mathfrak{S}^{\mathfrak{L}\mathfrak{W}})_x ~=~ \prod_{q \in X} \mathfrak{S}_{xq}^{(\mathfrak{L}\mathfrak{W})_q} ~=~ \prod_{q \in X} \mathfrak{S}_{xq}^{\sum_{p \in X} \mathfrak{L}_{qp} \mathfrak{W}_p} ~=~ \prod_{q \in X} \prod_{p \in X} \mathfrak{S}_{xq}^{\mathfrak{L}_{qp} \mathfrak{W}_p} \) |
| \((\mathfrak{L}\mathfrak{W})_q ~=~ \sum_{p \in X} \mathfrak{L}_{qp} \mathfrak{W}_p\) |
| \((\mathfrak{L}\mathfrak{W})_x ~=~ \sum_{p \in X} \mathfrak{L}_{xp} \mathfrak{W}_p\) |
| \(\mathrm{w} ~=~ \sum_{x \in X} \mathfrak{W}_x x \quad ?\) |
| \(\mathrm{w} ~=~ \sum_\mathbf{1} \mathrm{w}_\mathrm{X} \mathrm{X} \quad ?\) |
Commentary Note 12.7
- Problem about the relation of logical involution to the function space \(Y^X = \{ f : X \to Y \}.\)
- Notice that a function \(f : X \to Y\) is a "\(Y\!\)-evaluator of every \(X,\!\) or a "giver of a \(Y\!\)-value to every element of \(X\!\)".
Commentary on Selection 12 : Old Notes
|
Then |
| \((\mathit{s}^\mathit{l})^\mathrm{w}\!\) |
|
will denote whatever stands to every woman in the relation of servant of every lover of hers; and |
| \(\mathit{s}^{(\mathit{l}\mathrm{w})}\!\) |
|
will denote whatever is a servant of everything that is lover of a woman. So that |
| \((\mathit{s}^\mathit{l})^\mathrm{w} ~=~ \mathit{s}^{(\mathit{l}\mathrm{w})}.\) |
|
(Peirce, CP 3.77). |
Then we have the following results:
| \(\mathit{s}^{(\mathit{l}\mathrm{w})}\!\) | \(=\!\) | \(\bigcap_{x \in LW} \operatorname{proj}_1 (S \star x)\) | ||
| \((\mathit{s}^\mathit{l})^\mathrm{w}\!\) | \(=\!\) | \(\bigcap_{x \in W} \operatorname{proj}_1 (S^L \star x) \quad ???\) |
But what is \(S^L \quad ???\)
Suppose we try this:
| \(S^L ~=~ \bigcap_{x \in \operatorname{proj}_1 L} \operatorname{proj}_1 (S \star x)\) |
No, it looks like I need to think about this some more …
a b c d e f g h i o o o o o o o o o X / \ : | : | / \ 0 1 0 1 L / \ : | : | o o o o + - + + o X \ | / : : | | \ | / 0 0 1 1 S \|/ : : | | o o o o o o o o o X a b c d e f g h i |
It looks like there is a "servant of every lover of" link between \(i\!\) and \(j\!\) if and only if \(i \cdot S ~\supseteq~ L \cdot j.\) But the vacuous inclusions will make this non-intuitive.
Recall the analogy between involution and implication:
|
\( \begin{bmatrix} 0^0 & = & 1 \\ 0^1 & = & 0 \\ 1^0 & = & 1 \\ 1^1 & = & 1 \end{bmatrix} \qquad\qquad\qquad \begin{bmatrix} 0\!\Leftarrow\!0 & = & 1 \\ 0\!\Leftarrow\!1 & = & 0 \\ 1\!\Leftarrow\!0 & = & 1 \\ 1\!\Leftarrow\!1 & = & 1 \end{bmatrix} \) |
So it begins to look like this:
| \((\mathfrak{S}^\mathfrak{L})_{ab} ~=~ \prod_{x \in X} \mathfrak{S}_{ax}^{\mathfrak{L}_{xb}}\) |
In other words, \((\mathfrak{S}^\mathfrak{L})_{ab} = 0\) if and only if there exists an \(x \in X\) such that \(\mathfrak{S}_{ax} = 0\) and \(\mathfrak{L}_{xb} = 1.\)
Commentary on Selection 12 : Older Notes
The logic of terms is something of a lost art these days, when the current thinking in logic tends to treat the complete proposition as the quantum of discourse, ne plus infra. With absolute terms, or monadic relatives, and the simpler operations on dyadic relatives, the necessary translations between propositions and terms are obvious enough, but now that we've reached the threshold of higher adic relatives and operations as complex as exponentiation, it is useful to stop and consider the links between these two languages.
The term exponentiation is more generally used in mathematics for operations that involve taking a base to a power, and is slightly preferable to involution since the latter is used for different concepts in different contexts. Operations analogous to taking powers are widespread throughout mathematics and Peirce frequently makes use of them in a number of important applications, for example, in his theory of information. But that's another story.
The function space \(Y^X,\!\) where \(X\!\) and \(Y\!\) are sets, is the set of all functions from \(X\!\) to \(Y.\!\) An alternative notation for \(Y^X\!\) is \((X \to Y).\) Thus we have the following equivalents:
| \(\begin{matrix}Y^X & = & (X \to Y) & = & \{ f : X \to Y \}\end{matrix}\) |
If \(X\!\) and \(Y\!\) have cardinalities \(|X|\!\) and \(|Y|,\!\) respectively, then the function space \(Y^X\!\) has a cardinality given by the following equation:
| \(\begin{matrix}|Y^X| & = & |Y|^{|X|}\end{matrix}\) |
In the special case where \(Y = \mathbb{B} = \{ 0, 1 \},\) the function space \(\mathbb{B}^X\) is the set of functions \(\{ f : X \to \mathbb{B} \}.\) If the elements \(0, 1 \in \mathbb{B}\) are interpreted as the logical values \(\operatorname{false}, \operatorname{true},\) respectively, then a function of the type \(X \to \mathbb{B}\) may be interpreted as a proposition about the elements in \(X.\!\)
Really Old Commentary Notes
Up to this point in the discussion, we have observed that
the "number of" map 'v' : S -> R such that 'v's = [s] has
the following morphic properties:
0. [0] = 0
1. 'v'
2. x -< y => [x] =< [y]
3. [x +, y] =< [x] + [y]
contingent:
4. [xy] = [x][y]
view relation P c X x Y x Z as related to three functions:
`p_1` c
`p_3` c X x Y x Pow(Z)
f(x)
f(x+y) = f(x) + f(y)
f(p(x, y)) = q(f(x), f(y))
P(x, y, z)
(f^-1)(y)
f(z(x, y)) = z'(f(x), f(y))
Definition. f(x:y:z) = (fx:fy:fz).
f(x:y:z) = (fx:fy:
x:y:z in R => fx:fy:fz in fR
R(x, y, z) => (fR)(fx, fy, fz)
(L, x, y, z) => (fL, fx, fy, fz)
(x, y, z, L) => (xf, yf, zf, Lf)
(x, y, z, b) => (xf, yf, zf, bf)
fzxy = z'(fx)(fy)
F
o
|
o
/ \
o o
o
. | .
. | .
. | .
. o .
. / \ .
. / \ .
. / \ .
. o o .
. . .
. . .
.
C o . / \ . o
| . / \ . | CF
| . o o . |
f o . . . o fF
/ \ . . . / \
/ . \ . o o
X o o Y XF YF
<u, v, w> in P ->
o---------o---------o---------o---------o
| # h | h | f |
o=========o=========o=========o=========o
| P # X | Y | Z |
o---------o---------o---------o---------o
| Q # U | V | W |
o---------o---------o---------o---------o
Products of diagonal extensions:
1,1, = !1!!1!
= "anything that is anything that is ---"
= "anything that is ---"
= !1!
m,n = "man that is noble"
= (C:C +, I:I +, J:J +, O:O)(C +, D +, O)
= C +, O
n,m = "noble that is man"
= (C:C +, D:D +, O:O)(C +, I +, J +, O)
= C +, O
n,w = "noble that is woman"
= (C:C +, D:D +, O:O)(B +, D +, E)
= D
w,n = "woman that is noble"
= (B:B +, D:D +, E:E)(C +, D +, O)
= D
Given a set X and a subset M c X, define e_M,
the "idempotent representation" of M over X,
as the 2-adic relation e_M c X x X which is
the identity relation on M. In other words,
e_M = {<x, x> : x in M}.
Transposing this by steps into Peirce's notation:
e_M = {<x, x> : x in M}
= {x:x : x in M}
= Sum_X |x in M| x:x
'l' = "lover of ---"
's' = "servant of ---"
'l', = "lover that is --- of ---"
's', = "servant that is --- of ---"
| But not only may any absolute term be thus regarded as a relative term,
| but any relative term may in the same way be regarded as a relative with
| one correlate more. It is convenient to take this additional correlate
| as the first one.
|
| Then:
|
| 'l','s'w
|
| will denote a lover of a woman that is a servant of that woman.
|
| C.S. Peirce, CP 3.73
o---------o----+----o---------o---------o----+----o---------o
o-----------------------------o-----------------------------o
| Objective Framework (OF) | Interpretive Framework (IF) |
o-----------------------------o-----------------------------o
| Objects | Signs |
o-----------------------------o-----------------------------o
| |
| C o--------------- |
| |
| F o--------------- |
| |
| I o--------------- |
| |
| O o--------------- |
| |
| B o--------------- |
| |
| D o--------------- |
| |
| E o--------------- |
| o "m" |
| / |
| / |
| / |
| o o o-----------@ |
| \ |
| \ |
| \ |
| o |
| |
o-----------------------------o-----------------------------o
†‡||§¶
@#||$%
quality, reflection, synecdoche
1. neglect of
2. neglect of
3. neglect of nil?
Now, it's not the end of the story, of course, but it's a start.
The significant thing is what is usually the significant thing
in mathematics, at least, that two distinct descriptions refer
to the same things. Incidentally, Peirce is not really being
as indifferent to the distinctions between signs and things
as this ascii text makes him look, but uses a host of other
type-faces to distinguish the types and the uses of signs.
Discussion Notes
Discussion Note 1
GR = Gary Richmond
GR: I wonder if the necessary "elementary triad" spoken of
below isn't somehow implicated in those discussions
"invoking a 'closure principle'".
GR, quoting CSP:
| CP 1.292. It can further be said in advance, not, indeed,
| purely a priori but with the degree of apriority that is
| proper to logic, namely, as a necessary deduction from
| the fact that there are signs, that there must be an
| elementary triad. For were every element of the
| phaneron a monad or a dyad, without the relative
| of teridentity (which is, of course, a triad),
| it is evident that no triad could ever be
| built up. Now the relation of every sign
| to its object and interpretant is plainly
| a triad. A triad might be built up of
| pentads or of any higher perissad
| elements in many ways. But it
| can be proved -- and really
| with extreme simplicity,
| though the statement of
| the general proof is
| confusing -- that no
| element can have
| a higher valency
| than three.
GR: (Of course this passage also directly relates
to the recent thread on Identity and Teridentity.)
Yes, generally speaking, I think that there are deep formal principles here
that manifest themselves in these various guises: the levels of intention
or the orders of reflection, the sign relation, pragmatic conceivability,
the generative sufficiency of 3-adic relations for all practical intents,
and the irreducibility of continuous relations. I have run into themes
in combinatorics, group theory, and Lie algebras that are tantalizingly
reminiscent of the things that Peirce says here, but it will take me
some time to investigate them far enough to see what's going on.
GR: PS. I came upon the above passage last night reading through
the Peirce selections in John J. Stuhr's 'Classical American
Philosophy: Essential Readings and Interpretive Essays',
Oxford University, 1987 (the passage above is found on
pp 61-62), readily available in paperback in a new
edition, I believe.
GR: An aside: These excerpts in Sturh include versions of a fascinating
"Intellectual Autobiography", Peirce's summary of his scientific,
especially, philosophic accomplishments. I've seen them published
nowhere else.
Discussion Note 2
BU = Ben Udell
JA = Jon Awbrey
BU: I'm in the process of moving back to NYC and have had little opportunity
to do more than glance through posts during the past few weeks, but this
struck me because it sounds something I really would like to know about,
but I didn't understand it:
JA: Notice that Peirce follows the mathematician's usual practice,
then and now, of making the status of being an "individual" or
a "universal" relative to a discourse in progress. I have come
to appreciate more and more of late how radically different this
"patchwork" or "piecewise" approach to things is from the way of
some philosophers who seem to be content with nothing less than
many worlds domination, which means that they are never content
and rarely get started toward the solution of any real problem.
Just my observation, I hope you understand.
BU: "Many worlds domination", "nothing less than many worlds domination" --
as opposed to the patchwork or piecewise approach. What is many worlds
domination? When I hear "many worlds" I think of Everett's Many Worlds
interpretation of quantum mechanics.
Yes, it is a resonance of Edward, Everett, and All the Other Whos in Whoville,
but that whole microcosm is itself but the frumious reverberation of Leibniz's
Maenadolatry.
More sequitur, though, this is an issue that has simmered beneath
the surface of my consciousness for several decades now and only
periodically percolates itself over the hyper-critical thrashold
of expression. Let me see if I can a better job of it this time.
The topic is itself a patchwork of infernally recurrent patterns.
Here are a few pieces of it that I can remember arising recently:
| Zeroth Law Of Semantics
|
| Meaning is a privilege not a right.
| Not all pictures depict.
| Not all signs denote.
|
| Never confuse a property of a sign,
| for instance, existence,
| with a sign of a property,
| for instance, existence.
|
| Taking a property of a sign,
| for a sign of a property,
| is the zeroth sign of
| nominal thinking,
| and the first
| mistake.
|
| Also Sprach Zero*
A less catchy way of saying "meaning is a privilege not a right"
would most likely be "meaning is a contingency not a necessity".
But if I reflect on that phrase, it does not quite satisfy me,
since a deeper lying truth is that contingency and necessity,
connections in fact and connections beyond the reach of fact,
depend on a line of distinction that is itself drawn on the
scene of observation from the embodied, material, physical,
non-point massive, non-purely-spectrelative point of view
of an agent or community of interpretation, a discursive
universe, an engauged interpretant, a frame of at least
partial self-reverence, a hermeneutics in progress, or
a participant observer. In short, this distinction
between the contingent and the necessary is itself
contingent, which means, among other things, that
signs are always indexical at some least quantum.
Discussion Note 3
JR = Joe Ransdell
JR: Would the Kripke conception of the "rigid designator" be an instance
of the "many worlds domination"? I was struck by your speaking of
the "patchwork or piecewise" approach as well in that it seemed to
me you might be expressing the same general idea that I have usually
thought of in terms of contextualism instead: I mean the limits it
puts upon what you can say a priori if you really take contextualism
seriously, which is the same as recognizing indexicality as incapable
of elimination, I think.
Yes, I think this is the same ballpark of topics.
I can't really speak for what Kripke had in mind,
but I have a practical acquaintance with the way
that some people have been trying to put notions
like this to work on the applied ontology scene,
and it strikes me as a lot of nonsense. I love
a good parallel worlds story as much as anybody,
but it strikes me that many worlds philosophers
have the least imagination of anybody as to what
an alternative universe might really be like and
so I prefer to read more creative writers when it
comes to that. But serially, folks, I think that
the reason why some people evidently feel the need
for such outlandish schemes -- and the vast majority
of the literature on counterfactual conditionals falls
into the same spaceboat as this -- is simply that they
have failed to absorb, through the fault of Principian
filters, a quality that Peirce's logic is thoroughly
steeped in, namely, the functional interpretation
of logical terms, that is, as signs referring to
patterns of contingencies. It is why he speaks
more often, and certainly more sensibly and to
greater effect, of "conditional generals" than
of "modal subjunctives". This is also bound up
with that element of sensibility that got lost in
the transition from Peircean to Fregean quantifiers.
Peirce's apriorities are always hedged with risky bets.
Discussion Note 4
BU = Benjamin Udell
BU: I wish I had more time to ponder the "many-worlds" issue (& that my books
were not currently disappearing into heavily taped boxes). I had thought
of the piecemeal approach's opposite as the attempt to build a kind of
monolithic picture, e.g., to worry that there is not an infinite number
of particles in the physical universe for the infinity integers. But
maybe the business with rigid designators & domination of many worlds
has somehow to do with monolithism.
Yes, that's another way of saying it. When I look to my own priorities,
my big worry is that logic as a discipline is not fulfilling its promise.
I have worked in too many settings where the qualitative researchers and
the quantitative researchers could barely even talk to one an Other with
any understanding, and this I recognized as a big block to inquiry since
our first notice of salient facts and significant phenomena is usually
in logical, natural language, or qualitative forms, while our eventual
success in resolving anomalies and solving practical problems depends
on our ability to formalize, operationalize, and quantify the issues,
even if only to a very partial degree, as it generally turns out.
When I look to the history of how logic has been deployed in mathematics,
and through those media in science generally, it seems to me that the
Piece Train started to go off track with the 'Principia Mathematica'.
All pokes in the rib aside, however, I tend to regard this event
more as the symptom of a localized cultural phenomenon than as
the root cause of the broader malaise.
Discussion Note 5
CG = Clark Goble
JA = Jon Awbrey
JA, quoting CSP:
| For example,
|
| f + u
|
| means all Frenchmen besides all violinists, and,
| therefore, considered as a logical term, implies
| that all French violinists are 'besides themselves'.
CG: Could you clarify your use of "besides"?
CG: I think I am following your thinking in that you
don't want the logical terms to be considered
to have any necessary identity between them.
Is that right?
I use vertical sidebars "|" for long quotations, so this
is me quoting Peirce at CP 3.67 who is explaining in an
idiomatic way Boole's use of the plus sign for a logical
operation that is strictly speaking limited to terms for
mutually exclusive classes. The operation would normally
be extended to signify the "symmetric difference" operator.
But Peirce is saying that he prefers to use the sign "+,"
for inclusive disjunction, corresponding to the union of
the associated classes. Peirce calls Boole's operation
"invertible" because it amounts to the sum operation in
a field, whereas the inclusive disjunction or union is
"non-invertible", since knowing that A |_| B = C does
not allow one to say determinately that A = C - B.
I can't recall if Boole uses this 'besides' idiom,
but will check later.
Discussion Note 6
CG = Clark Goble
JA = Jon Awbrey
JA: I use vertical sidebars "|" for long quotations, so this
is me quoting Peirce at CP 3.67 who is explaining in an
idiomatic way Boole's use of the plus sign for a logical
operation that is strictly speaking limited to terms for
mutually exclusive classes.
CG: Is that essay related to any of the essays
in the two volume 'Essential Peirce'? I'm
rather interested in how he speaks there.
No, the EP volumes are extremely weak on logical selections.
I see nothing there that deals with the logic of relatives.
JA: But Peirce is saying that he prefers to use the sign "+,"
for inclusive disjunction, corresponding to the union of
the associated classes.
CG: The reason I asked was more because it seemed
somewhat interesting in light of the logic of
operators in quantum mechanics. I was curious
if the use of "beside" might relate to that.
But from what you say it probably was just me
reading too much into the quote. The issue of
significance was whether the operation entailed
the necessity of mutual exclusivity or whether
some relationship between the classes might be
possible. I kind of latched on to Peirce's
odd statement about "all French violinists
are 'beside themselves'".
CG: Did Peirce have anything to say about
what we'd call non-commuting operators?
In general, 2-adic relative terms are non-commutative.
For example, a brother of a mother is not identical to
a mother of a brother.
Discussion Note 7
GR = Gary Richmond
GR: I am very much enjoying, which is to say,
learning from your interlacing commentary
on Peirce's 1870 "Logic of Relatives" paper.
GR: What an extraordinary paper the 1870 "LOG" is! Your notes helped
me appreciate the importance of the unanticipated proposal of P's
to "assign to all logical terms, numbers". On the other hand,
the excerpts suggested to we why Peirce finally framed his
Logic of Relatives into graphical form. Still, I think
that a thorough examination of the 1970 paper might
serve as propaedeutic (and of course, much more)
for the study of the alpha and beta graphs.
Yes, there's gold in them thar early logic papers that has been "panned"
but nowhere near mined in depth yet. The whole quiver of arrows between
terms and numbers harks back to the 'numeri characteristici' of Leibniz,
of course, but Leibniz attended more on the intensional chains of being
while Peirce will here start to "escavate" the extensional hierarchies.
I consider myself rewarded that you see the incipient impulse toward
logical graphs, as one of the most striking things to me about this
paper is to see these precursory seeds already planted here within
it and yet to know how long it will take them to sprout and bloom.
Peirce is obviously struggling to stay within the linotyper's art --
a thing that we, for all our exorbitant hype about markable text,
are still curiously saddled with -- but I do not believe that it
is possible for any mind equipped with a geometrical imagination
to entertain these schemes for connecting up terminological hubs
with their terminological terminals without perforce stretching
imaginary strings between the imaginary gumdrops.
GR: I must say though that the pace at which you've been throwing this at us
is not to be kept up with by anyone I know "in person or by reputation".
I took notes on the first 5 or 6 Notes, but can now just barely find
time to read through your posts.
Oh, I was trying to burrow as fast as I could toward the more untapped veins --
I am guessing that things will probably "descalate" a bit over the next week,
but then, so will our attention spans ...
Speaking of which, I will have to break here, and pick up the rest later ...
Discussion Note 8
GR = Gary Richmond
GR: In any event, I wish that you'd comment on Note 5 more directly (though
you do obliquely in your own diagramming of "every [US] Vice-President(s) ...
[who is] every President(s) of the US Senate".
There are several layers of things to say about that,
and I think that it would be better to illustrate the
issues by way of the examples that Peirce will soon be
getting to, but I will see what I can speak to for now.
GR: But what interested me even more in LOR, Note 5, was the sign < ("less than"
joined to the sign of identity = to yield P's famous sign -< (or more clearly,
=<) of inference, which combines the two (so that -< (literally, "as small as")
means "is". I must say I both "get" this and don't quite (Peirce's example(s) of
the frenchman helped a little). Perhaps your considerably more mathematical mind
can help clarify this for a non-mathematician such as myself. (My sense is that
"as small as" narrows the terms so that "everything that occurs in the conclusion
is already contained in the premise.) I hope I'm not being obtuse here. I'm sure
it's "all too simple for words".
Then let us draw a picture.
"(F (G))", read "not F without G", means that F (G), that is, F and not G,
is the only region exempted from the occupation of being in this universe:
o-----------------------------------------------------------o
|`X`````````````````````````````````````````````````````````|
|```````````````````````````````````````````````````````````|
|`````````````o-------------o```o-------------o`````````````|
|````````````/ \`/```````````````\````````````|
|```````````/ o`````````````````\```````````|
|``````````/ /`\`````````````````\``````````|
|`````````/ /```\`````````````````\`````````|
|````````/ /`````\`````````````````\````````|
|```````o o```````o`````````````````o```````|
|```````| |```````|`````````````````|```````|
|```````| |```````|`````````````````|```````|
|```````| F |```````|````````G````````|```````|
|```````| |```````|`````````````````|```````|
|```````| |```````|`````````````````|```````|
|```````o o```````o`````````````````o```````|
|````````\ \`````/`````````````````/````````|
|`````````\ \```/`````````````````/`````````|
|``````````\ \`/`````````````````/``````````|
|```````````\ o`````````````````/```````````|
|````````````\ /`\```````````````/````````````|
|`````````````o-------------o```o-------------o`````````````|
|```````````````````````````````````````````````````````````|
|```````````````````````````````````````````````````````````|
o-----------------------------------------------------------o
Collapsing the vacuous region like soapfilm popping on a wire frame,
we draw the constraint (F (G)) in the following alternative fashion:
o-----------------------------------------------------------o
|`X`````````````````````````````````````````````````````````|
|```````````````````````````````````````````````````````````|
|```````````````````````````````o-------------o`````````````|
|``````````````````````````````/```````````````\````````````|
|`````````````````````````````o`````````````````\```````````|
|````````````````````````````/`\`````````````````\``````````|
|```````````````````````````/```\`````````````````\`````````|
|``````````````````````````/`````\`````````````````\````````|
|`````````````````````````o```````o`````````````````o```````|
|`````````````````````````|```````|`````````````````|```````|
|`````````````````````````|```````|`````````````````|```````|
|`````````````````````````|```F```|````````G````````|```````|
|`````````````````````````|```````|`````````````````|```````|
|`````````````````````````|```````|`````````````````|```````|
|`````````````````````````o```````o`````````````````o```````|
|``````````````````````````\`````/`````````````````/````````|
|```````````````````````````\```/`````````````````/`````````|
|````````````````````````````\`/`````````````````/``````````|
|`````````````````````````````o`````````````````/```````````|
|``````````````````````````````\```````````````/````````````|
|```````````````````````````````o-------------o`````````````|
|```````````````````````````````````````````````````````````|
|```````````````````````````````````````````````````````````|
o-----------------------------------------------------------o
So, "(F (G))", "F => G", "F =< G", "F -< G", "F c G",
under suitable mutations of interpretation, are just
so many ways of saying that the denotation of "F" is
contained within the denotation of "G".
Now, let us look to the "characteristic functions" or "indicator functions"
of the various regions of being. It is frequently convenient to ab-use the
same letters for them and merely keep a variant interpretation "en thy meme",
but let us be more meticulous here, and reserve the corresponding lower case
letters "f" and "g" to denote the indicator functions of the regions F and G,
respectively.
Taking B = {0, 1} as the boolean domain, we have:
f, g : X -> B
(f^(-1))(1) = F
(g^(-1))(1) = G
In general, for h : X -> B, an expression like "(h^(-1))(1)"
can be read as "the inverse of h evaluated at 1", in effect,
denoting the set of points in X where h evaluates to "true".
This is called the "fiber of truth" in h, and I have gotten
where I like to abbreviate it as "[|h|]".
Accordingly, we have:
F = [|f|] = (f^(-1))(1) c X
G = [|g|] = (g^(-1))(1) c X
This brings us to the question, what sort
of "functional equation" between f and g
goes with the regional constraint (F (G))?
Just this, that f(x) =< g(x) for all x in X,
where the '=<' relation on the values in B
has the following operational table for
the pairing "row head =< column head".
o---------o---------o---------o
| =< # 0 | 1 |
o=========o=========o=========o
| 0 # 1 | 1 |
o---------o---------o---------o
| 1 # 0 | 1 |
o---------o---------o---------o
And this, of course, is the same thing as the truth table
for the conditional connective or the implication relation.
GR: By the way, in the semiosis implied by the modal gamma graphs,
could -< (were it used there, which of course it is not) ever
be taken to mean,"leads to" or "becomes" or "evolves into"?
I informally use it that way myself, using the ordinary
arrow for implication.
I am a bit insensitive to the need for modal logic,
since necessity in mathematics always seems to come
down to being a matter of truth for all actual cases,
if under an expanded sense of actuality that makes it
indiscernible from possibility, so I must beg off here.
But there are places where Peirce makes a big deal about
the advisability of drawing the '-<' symbol in one fell
stroke of the pen, kind of like a "lazy gamma" -- an old
texican cattle brand -- and I have seen another place where
he reads "A -< B" as "A, in every way that it can be, is B",
as if this '-<' fork in the road led into a veritable garden
of branching paths.
And out again ...
Discussion Note 9
GR = Gary Richmond
JA = Jon Awbrey
JA: I am a bit insensitive to the need for modal logic,
since necessity in mathematics always seems to come
down to being a matter of truth for all actual cases,
if under an expanded sense of actuality that makes it
indiscernible from possibility, so I must beg off here.
GR: I cannot agree with you regarding modal logic. Personally
I feel that the gamma part of the EG's is of the greatest
interest and potential importance, and as Jay Zeman has
made clear in his dissertation, Peirce certainly thought
this as well.
You disagree that I am insensitive? Well, certainly nobody has ever done that before!
No, I phrased it that way to emphasize the circumstance that it ever hardly comes up
as an issue within the limited purview of my experience, and when it does -- as in
topo-logical boundary situations -- it seems to require a sort of analysis that
doesn't comport all that well with the classical modes and natural figures of
speech about it. Then again, I spent thirty years trying to motorize Alpha,
have only a few good clues how I would go about Beta, and so Gamma doesn't
look like one of those items on my plate.
Speeching Of Which ---
Best Of The Season ...
And Happy Trailing ...
Discussion Note 10
BM = Bernard Morand
JA = Jon Awbrey
BM: Thanks for your very informative talk. There
is a point that I did not understand in note 35:
JA: If we operate in accordance with Peirce's example of `g`'o'h
as the "giver of a horse to an owner of that horse", then we
may assume that the associative law and the distributive law
are by default in force, allowing us to derive this equation:
JA: 'l','s'w = 'l','s'(B +, D +, E) = 'l','s'B +, 'l','s'D +, 'l','s'E
BM: May be because language or more probably my lack of training in logic, what
does mean that "associative law and distributive law are by default in force"?
Those were some tricky Peirces,
and I was trying to dodge them
as artful as could be, but now
you have fastly apprehended me!
It may be partly that I left out the initial sections of this paper where Peirce
discusses how he will regard the ordinarily applicable principles in the process
of trying to extend and generalize them (CP 3.45-62), but there may be also an
ambiguity in Peirce's use of the phrase "absolute conditions" (CP 3.62-68).
Does he mean "absolutely necessary", "indispensable", "inviolate", or
does he mean "the conditions applying to the logic of absolute terms",
in which latter case we would expect to alter them sooner or later?
We lose the commutative law, xy = yx, as soon as we extend to 2-adic relations,
but keep the associative law, x(yz) = (xy)z, as the multiplication of 2-adics
is the logical analogue of ordinary matrix multiplication, and Peirce like
most mathematicians treats the double distributive law, x(y + z) = xy + xz
and (x + y)z = xz + yz, and as something that must be striven to preserve
as far as possible.
Strictly speaking, Peirce is already using a principle that goes beyond
the ordinary associative law, but that is recognizably analogous to it,
for example, in the modified Othello case, where (J:J:D)(J:D)(D) = J.
If it were strictly associative, then we would have the following:
1. (J:J:D)((J:D)(D)) = (J:J:D)(J) = 0?
2. ((J:J:D)(J:D))(D) = (J)(D) = 0?
In other words, the intended relational linkage would be broken.
However, the type of product that Peirce is taking for granted
in this situation often occurs in mathematics in just this way.
There is another location where he comments more fully on this,
but I have the sense that it was a late retrospective remark,
and I do not recall if it was in CP or in the microfilm MS's
that I read it.
By "default" conditions I am referring more or less to what
Peirce says at the end of CP 3.69, where he use an argument
based on the distributive principle to rationalize the idea
that 'A term multiplied by two relatives shows that the same
individual is in the two relations'. This means, for example,
that one can let "`g`'o'h", without subjacent marks or numbers,
be interpreted on the default convention of "overlapping scopes",
where the two correlates of `g` are given by the next two terms
in line, namely, 'o' and h, and the single correlate of 'o' is
given by the very next term in line, namely, h. Thus, it is
only when this natural scoping cannot convey the intended
sense that we have to use more explicit mark-up devices.
BM: About another point: do you think that the LOR could be of some help to solve
the puzzle of the "second way of dividing signs" where CSP concludes that 66
classes could be made out of the 10 divisions (Letters to lady Welby)?
(As I see them, the ten divisions involve a mix of relative terms,
dyadic relations and a triadic one. In order to make 66 classes
it is clear that these 10 divisions have to be stated under some
linear order. The nature of this order is at the bottom of the
disagreements on the subject).
This topic requires a longer excuse from me
than I am able to make right now, but maybe
I'll get back to it later today or tomorrow.
Discussion Note 11
BM = Bernard Morand
BM: About another point: do you think that the LOR could be of some help
to solve the puzzle of the "second way of dividing signs" where CSP
concludes that 66 classes could be made out of the 10 divisions
(Letters to lady Welby)? (As I see them, the ten divisions
involve a mix of relative terms, dyadic relations and
a triadic one. In order to make 66 classes it is
clear that these 10 divisions have to be stated
under some linear order. The nature of this
order is at the bottom of the disagreements
on the subject).
Yes. At any rate, I have a pretty clear sense from reading Peirce's work
in the period 1865-1870 that the need to understand the function of signs
in scientific inquiry is one of the main reasons he found himself forced
to develop both the theory of information and the logic of relatives.
Peirce's work of this period is evenly distributed across the extensional
and intensional pans of the balance in a way that is very difficult for us
to follow anymore. I remember when I started looking into this I thought of
myself as more of an "intensional, synthetic" than an "extensional, analytic"
type of thinker, but that seems like a long time ago, as it soon became clear
that much less work had been done in the Peirce community on the extensional
side of things, while that was the very facet that needed to be polished up
in order to reconnect logic with empirical research and mathematical models.
So I fear that I must be content that other able people are working on the
intensional classification of sign relations.
Still, the way that you pose the question is very enticing,
so maybe it is time for me to start thinking about this
aspect of sign relations again, if you could say more
about it.
Discussion Note 12
BM = Bernard Morand
BM: The pairing "intensional, synthetic" against the other "extensional, analytic"
is not one that I would have thought so. I would have paired synthetic with
extensional because synthesis consists in adding new facts to an already made
conception. On the other side analysis looks to be the determination of
features while neglecting facts. But may be there is something like
a symmetry effect leading to the same view from two different points.
Oh, it's not too important, as I don't put a lot of faith in such divisions,
and the problem for me is always how to integrate the facets of the object,
or the faculties of the mind -- but there I go being synthetic again!
I was only thinking of a conventional contrast that used to be drawn
between different styles of thinking in mathematics, typically one
points to Descartes, and the extensionality of analytic geometry,
versus Desargues, and the intensionality of synthetic geometry.
It may appear that one has side-stepped the issue of empiricism
that way, but then all that stuff about the synthetic a priori
raises its head, and we have Peirce's insight that mathematics
is observational and even experimental, and so I must trail off
into uncoordinated elliptical thoughts ...
The rest I have to work at a while, and maybe go back to the Welby letters.
Discussion Note 13
BM = Bernard Morand
BM: I will try to make clear the matter, at least as far as I understand it
for now. We can summarize in a table the 10 divisions with their number
in a first column, their title in current (peircean) language in the second
and some kind of logical notation in the third. The sources come mainly from
the letters to Lady Welby. While the titles come from CP 8.344, the third column
comes from my own interpretation.
BM: So we get:
I - According to the Mode of Apprehension of the Sign itself - S
II - According to the Mode of Presentation of the Immediate Object - Oi
III - According to the Mode of Being of the Dynamical Object - Od
IV - According to the Relation of the Sign to its Dynamical Object - S-Od
V - According to the Mode of Presentation of the Immediate Interpretant - Ii
VI - According to the Mode of Being of the Dynamical Interpretant - Id
VII - According to the relation of the Sign to the Dynamical Interpretant - S-Id
VIII - According to the Nature of the Normal Interpretant - If
IX - According to the the relation of the Sign to the Normal Interpretant - S-If
X - According to the Triadic Relation of the Sign to its Dynamical Object
and to its Normal Interpretant - S-Od-If
For my future study, I will reformat the table in a way that I can muse upon.
I hope the roman numerals have not become canonical, as I cannot abide them.
Table. Ten Divisions of Signs (Peirce, Morand)
o---o---------------o------------------o------------------o---------------o
| | According To: | Of: | To: | |
o===o===============o==================o==================o===============o
| 1 | Apprehension | Sign Itself | | S |
| 2 | Presentation | Immediate Object | | O_i |
| 3 | Being | Dynamical Object | | O_d |
| 4 | Relation | Sign | Dynamical Object | S : O_d |
o---o---------------o------------------o------------------o---------------o
| 5 | Presentation | Immediate Interp | | I_i |
| 6 | Being | Dynamical Interp | | I_d |
| 7 | Relation | Sign | Dynamical Interp | S : I_d |
o---o---------------o------------------o------------------o---------------o
| 8 | Nature | Normal Interp | | I_f |
| 9 | Relation | Sign | Normal Interp | S : I_f |
o---o---------------o------------------o------------------o---------------o
| A | Relation | Sign | Dynamical Object | |
| | | | & Normal Interp | S : O_d : I_f |
o---o---------------o------------------o------------------o---------------o
Just as I have always feared, this classification mania
appears to be communicable! But now I must definitely
review the Welby correspondence, as all this stuff was
a blur to my sensibilities the last 10 times I read it.
Discussion Note 14
BM = Bernard Morand
[Table. Ten Divisions of Signs (Peirce, Morand)]
BM: Yes this is clearer (in particular in expressing relations with :)
This is what Peirce used to form elementary relatives, for example,
o:s:i = <o, s, i>, and I find it utterly ubertous in a wide variety
of syntactic circumstances.
BM: I suggest making a correction to myself if
the table is destinate to become canonic.
Hah! Good one!
BM: I probably made a too quick jump from Normal Interpretant to Final Interpretant.
As we know, the final interpretant, the ultimate one is not a sign for Peirce
but a habit. So for the sake of things to come it would be more careful to
retain I_n in place of I_f for now.
This accords with my understanding of how the word is used in mathematics.
In my own work it has been necessary to distinguish many different species
of expressions along somewhat similar lines, for example: arbitrary, basic,
canonical, decidable, normal, periodic, persistent, prototypical, recurrent,
representative, stable, typical, and so on. So I will make the changes below:
Table. Ten Divisions of Signs (Peirce, Morand)
o---o---------------o------------------o------------------o---------------o
| | According To: | Of: | To: | |
o===o===============o==================o==================o===============o
| 1 | Apprehension | Sign Itself | | S |
| 2 | Presentation | Immediate Object | | O_i |
| 3 | Being | Dynamical Object | | O_d |
| 4 | Relation | Sign | Dynamical Object | S : O_d |
o---o---------------o------------------o------------------o---------------o
| 5 | Presentation | Immediate Interp | | I_i |
| 6 | Being | Dynamical Interp | | I_d |
| 7 | Relation | Sign | Dynamical Interp | S : I_d |
o---o---------------o------------------o------------------o---------------o
| 8 | Nature | Normal Interp | | I_n |
| 9 | Relation | Sign | Normal Interp | S : I_n |
o---o---------------o------------------o------------------o---------------o
| A | Tri. Relation | Sign | Dynamical Object | |
| | | | & Normal Interp | S : O_d : I_n |
o---o---------------o------------------o------------------o---------------o
BM: Peirce gives the following definition (CP 8.343):
BM, quoting CSP:
| It is likewise requisite to distinguish
| the 'Immediate Interpretant', i.e. the
| Interpretant represented or signified in
| the Sign, from the 'Dynamic Interpretant',
| or effect actually produced on the mind
| by the Sign; and both of these from
| the 'Normal Interpretant', or effect
| that would be produced on the mind by
| the Sign after sufficient development
| of thought.
|
| C.S. Peirce, 'Collected Papers', CP 8.343.
Well, you've really tossed me in the middle of the briar patch now!
I must continue with my reading from the 1870 LOR, but now I have
to add to my do-list the problems of comparing the whole variorum
of letters and drafts of letters to Lady Welby. I only have the
CP 8 and Wiener versions here, so I will depend on you for ample
excerpts from the Lieb volume.
Discussion Note 15
I will need to go back and pick up the broader contexts of your quotes. For ease of study I break Peirce's long paragraphs into smaller pieces. | It seems to me that one of the first useful steps toward a science | of 'semeiotic' ([Greek 'semeiootike']), or the cenoscopic science | of signs, must be the accurate definition, or logical analysis, | of the concepts of the science. | | I define a 'Sign' as anything which on the one hand | is so determined by an Object and on the other hand | so determines an idea in a person's mind, that this | latter determination, which I term the 'Interpretant' | of the sign, is thereby mediately determined by that | Object. | | A sign, therefore, has a triadic relation to | its Object and to its Interpretant. But it is | necessary to distinguish the 'Immediate Object', | or the Object as the Sign represents it, from | the 'Dynamical Object', or really efficient | but not immediately present Object. | | It is likewise requisite to distinguish | the 'Immediate Interpretant', i.e. the | Interpretant represented or signified in | the Sign, from the 'Dynamic Interpretant', | or effect actually produced on the mind | by the Sign; and both of these from | the 'Normal Interpretant', or effect | that would be produced on the mind by | the Sign after sufficient development | of thought. | | On these considerations I base a recognition of ten respects in which Signs | may be divided. I do not say that these divisions are enough. But since | every one of them turns out to be a trichotomy, it follows that in order | to decide what classes of signs result from them, I have 3^10, or 59049, | difficult questions to carefully consider; and therefore I will not | undertake to carry my systematical division of signs any further, | but will leave that for future explorers. | | C.S. Peirce, 'Collected Papers', CP 8.343. You never know when the future explorer will be yourself.
Discussion Note 16
Burks, the editor of CP 8, attaches this footnote to CP 8.342-379, "On the Classification of Signs": | From a partial draft of a letter to Lady Welby, bearing | the dates of 24, 25, and 28 December 1908, Widener IB3a, | with an added quotation in 368n23. ... There is a passage roughly comparable to CP 8.343 in a letter to Lady Welby dated 23 December 1908, pages 397-409 in Wiener, which is incidentally the notorious "sop to Cerberus" letter: | It is usual and proper to distinguish two Objects of a Sign, | the Mediate without, and the Immediate within the Sign. Its | Interpretant is all that the Sign conveys: acquaintance with | its Object must be gained by collateral experience. | | The Mediate Object is the Object outside of the Sign; I call | it the 'Dynamoid' Object. The Sign must indicate it by a hint; | and this hint, or its substance, is the 'Immediate' Object. | | Each of these two Objects may be said to be capable of either of | the three Modalities, though in the case of the Immediate Object, | this is not quite literally true. | | Accordingly, the Dynamoid Object may be a Possible; when I term | the Sign an 'Abstractive'; such as the word Beauty; and it will be | none the less an Abstractive if I speak of "the Beautiful", since it is | the ultimate reference, and not the grammatical form, that makes the sign | an 'Abstractive'. | | When the Dynamoid Object is an Occurrence (Existent thing or Actual fact | of past or future), I term the Sign a 'Concretive'; any one barometer | is an example; and so is a written narrative of any series of events. | | For a 'Sign' whose Dynamoid Object is a Necessitant, I have at present | no better designation than a 'Collective', which is not quite so bad a | name as it sounds to be until one studies the matter: but for a person, | like me, who thinks in quite a different system of symbols to words, it | is so awkward and often puzzling to translate one's thought into words! | | If the Immediate Object is a "Possible", that is, if the Dynamoid Object | is indicated (always more or less vaguely) by means of its Qualities, etc., | I call the Sign a 'Descriptive'; | | if the Immediate is an Occurrence, I call the Sign a 'Designative'; | | and if the Immediate Object is a Necessitant, I call the Sign a | 'Copulant'; for in that case the Object has to be so identified | by the Interpreter that the Sign may represent a necessitation. | My name is certainly a temporary expedient. | | It is evident that a possible can determine nothing but a Possible, | it is equally so that a Necessitant can be determined by nothing but | a Necessitant. Hence it follows from the Definition of a Sign that | since the Dynamoid Object determines the Immediate Object, | | Which determines the Sign itself, | which determines the Destinate Interpretant | which determines the Effective Interpretant | which determines the Explicit Interpretant | | the six trichotomies, instead of determining 729 classes of signs, | as they would if they were independent, only yield 28 classes; | and if, as I strongly opine (not to say almost prove), there | are four other trichotomies of signs of the same order of | importance, instead of making 59,049 classes, these will | only come to 66. | | The additional 4 trichotomies are undoubtedly, first: | | Icons*, Symbols, Indices, | |*(or Simulacra, Aristotle's 'homoiomata'), caught from Plato, who I guess took it | from the Mathematical school of logic, for it earliest appears in the 'Phaedrus' | which marks the beginning of Plato's being decisively influenced by that school. | Lutoslowski is right in saying that the 'Phaedrus' is later than the 'Republic' | but his date 379 B.C. is about eight years too early. | | and then 3 referring to the Interpretants. One of these I am pretty confident | is into: 'Suggestives', 'Imperatives', 'Indicatives', where the Imperatives | include the Interrogatives. Of the other two I 'think' that one must be | into Signs assuring their Interpretants by: | | Instinct, Experience, Form. | | The other I suppose to be what, in my 'Monist' | exposition of Existential Graphs, I called: | | Semes, Phemes, Delomes. | | CSP, 'Selected Writings', pp. 406-408. | |'Charles S. Peirce: Selected Writings (Values in a Universe of Chance)', | edited with an introduction and notes by Philip P. Wiener, Dover, | New York, NY, 1966. Originally published under the subtitle | in parentheses above, Doubleday & Company, 1958. But see CP 4.549-550 for a significant distinction between the categories (or modalities) and the orders of intention.
Discussion Note 17
HC = Howard Callaway
JA = Jon Awbrey
JA: In closing, observe that the teridentity relation has turned up again
in this context, as the second comma-ing of the universal term itself:
1,, = B:B:B +, C:C:C +, D:D:D +, E:E:E +, I:I:I +, J:J:J +, O:O:O.
HC: I see that you've come around to a mention of teridentity again, Jon.
Still, if I recall the prior discussions, then no one doubts that we
can have a system of notation in which teridentity appears (I don't
actually see it here).
Perhaps we could get at the root of the misunderstanding
if you tell me why you don't actually see the concept of
teridentity being exemplified here.
If it's only a matter of having lost the context of the
present discussion over the break, then you may find the
previous notes archived at the distal ends of the ur-links
that I append below (except for the first nine discussion
notes that got lost in a disk crash at the Arisbe Dev site).
HC: Also, I think we can have a system of notation in which
teridentity is needed. Those points seem reasonably clear.
The advantage of a concept is the integration of a species of manifold.
The necessity of a concept is the incapacity to integrate it otherwise.
Of course, no one should be too impressed with a concept that
is only the artifact of a particular system of representation.
So before we accord a concept the status of addressing reality,
and declare it a term of some tenured office in our intellects,
we would want to see some evidence that it helps us to manage
a reality that we cannot see a way to manage any other way.
Granted.
Now how in general do we go about an investiture of this sort?
That is the big question that would serve us well to consider
in the process of the more limited investigation of identity.
Indeed, I do not see how it is possible to answer the small
question if no understanding is reached on the big question.
HC: What remains relatively unclear is why we should need a system of notation
in which teridentity appears or is needed as against one in which it seems
not to be needed -- since assertion of identity can be made for any number
of terms in the standard predicate calculus.
This sort of statement totally non-plusses me.
It seems like a complete non-sequitur or even
a contradiction in terms to me.
The question is about the minimal adequate resource base for
defining, deriving, or generating all of the concepts that we
need for a given but very general type of application that we
conventionally but equivocally refer to as "logic". You seem
to be saying something like this: We don't need 3-identity
because we have 4-identity, 5-identity, 6-identity, ..., in
the "standard predicate calculus". The question is not what
concepts are generated in all the generations that follow the
establishment of the conceptual resource base (axiom system),
but what is the minimal set of concepts that we can use to
generate the needed collection of concepts. And there the
answer is, in a way that is subject to the usual sorts of
mathematical proof, that 3-identity is the minimum while
2-identity is not big enough to do the job we want to do.
Logic Of Relatives 01-41, LOR Discussion Notes 10-17.
Discussion Note 18
BM = Bernard Morand
JA = Jon Awbrey
JA: but now I have to add to my do-list the problems of comparing the
whole variorum of letters and drafts of letters to Lady Welby.
I only have the CP 8 and Wiener versions here, so I will
depend on you for ample excerpts from the Lieb volume.
BM: I made such a kind of comparison some time ago. I selected
the following 3 cases on the criterium of alternate "grounds".
Hoping it could save some labor. The first rank expressions
come from the MS 339 written in Oct. 1904 and I label them
with an (a). I think that it is interesting to note that
they were written four years before the letters to Welby
and just one or two years after the Syllabus which is the
usual reference for the classification in 3 trichotomies
and 10 classes. The second (b) is our initial table (from
a draft to Lady Welby, Dec. 1908, CP 8.344) and the third
(c) comes from a letter sent in Dec. 1908 (CP 8.345-8.376).
A tabular presentation would be better but I can't do it.
Comparing (c) against (a) and (b) is informative, I think.
Is this anywhere that it can be linked to from Arisbe?
I've seen many pretty pictures of these things over the
years, but may have to follow my own gnosis for a while.
Pages I have bookmarked just recently,
but not really had the chance to study:
http://www.digitalpeirce.org/hoffmann/p-sighof.htm
http://www.csd.uwo.ca/~merkle/thesis/Introduction.html
http://members.door.net/arisbe/menu/library/aboutcsp/merkle/hci-abstract.htm
Discussion Note 19
BM = Bernard Morand
JA = Jon Awbrey
I now have three partially answered messages on the table,
so I will just grab this fragment off the top of the deck.
BM: Peirce gives the following definition (CP 8.343):
BM, quoting CSP:
| It is likewise requisite to distinguish
| the 'Immediate Interpretant', i.e. the
| Interpretant represented or signified in
| the Sign, from the 'Dynamic Interpretant',
| or effect actually produced on the mind
| by the Sign; and both of these from
| the 'Normal Interpretant', or effect
| that would be produced on the mind by
| the Sign after sufficient development
| of thought.
|
| C.S. Peirce, 'Collected Papers', CP 8.343.
JA: Well, you've really tossed me in the middle of the briar patch now!
I must continue with my reading from the 1870 LOR, ...
BM: Yes indeed! I am irritated by having not the necessary
turn of mind to fully grasp it. But it seems to be a
prerequisite in order to understand the very meaning
of the above table. It could be the same for:
BM, quoting CSP:
| I define a 'Sign' as anything which on the one hand
| is so determined by an Object and on the other hand
| so determines an idea in a person's mind, that this
| latter determination, which I term the 'Interpretant'
| of the sign, is thereby mediately determined by that
| Object.
BM: The so-called "latter determination" would make the 'Interpretant'
a tri-relative term into a teridentity involving Sign and Object.
Isn't it?
BM: I thought previously that the Peirce's phrasing was just applying the
principle of transitivity. From O determines S and S determines I,
it follows: O determines I. But this is not the same as teridentity.
Do you think so or otherwise?
My answers are "No" and "Otherwise".
Continuing to discourse about definite universes thereof,
the 3-identity term over the universe 1 = {A, B, C, D, ...} --
I only said it was definite, I didn't say it wasn't vague! --
designates, roughly speaking, the 3-adic relation that may
be hinted at by way of the following series:
1,, = A:A:A +, B:B:B +, C:C:C +, D:D:D +, ...
I did a study on Peirce's notion of "determination".
As I understand it so far, we need to keep in mind
that it is more fundamental than causation, can be
a form of "partial determination", and is roughly
formal, mathematical, or "information-theoretic",
not of necessity invoking any temporal order.
For example, when we say "The points A and B determine the line AB",
this invokes the concept of a 3-adic relation of determination that
does not identify A, B, AB, is not transitive, as transitivity has
to do with the composition of 2-adic relations and would amount to
the consideration of a degenerate 3-adic relation in this context.
Now, it is possible to have a sign relation q whose sum enlists
an elementary sign relation O:S:I where O = S = I. For example,
it makes perfect sense to me to say that the whole universe may
be a sign of itself to itself, so the conception is admissable.
But this amounts to a very special case, by no means general.
More generally, we are contemplating sums like the following:
q = O1:S1:I1 +, O2:S2:I2 +, O3:S3:I3 +, ...
Discussion Note 20
HC = Howard Callaway
JR = Joe Ransdell
HC: Though I certainly hesitate to think that we are separated
from the world by a veil of signs, it seems clear, too, on
Peircean grounds, that no sign can ever capture its object
completely.
JR: Any case of self-representation is a case of sign-object identity,
in some sense of "identity". I have argued in various places that
this is the key to the doctrine of immediate perception as it occurs
in Peirce's theory.
To put the phrase back on the lathe:
| We are not separated from the world by a veil of signs --
| we are the veil of signs.
Discussion Note 21
AS = Armando Sercovich
AS: We are not separated from the world by a veil of signs nor we are a veil of signs.
Simply we are signs.
AS, quoting CSP:
| The *man-sign* acquires information, and comes to mean more than he did before.
| But so do words. Does not electricity mean more now than it did in the days
| of Franklin? Man makes the word, and the word means nothing which the man
| has not made it mean, and that only to some man. But since man can think
| only by means of words or other external symbols, these might turn round
| and say: "You mean nothing which we have not taught you, and then only
| so far as you address some word as the interpretant of your thought".
| In fact, therefore, men and words reciprocally educate each other;
| each increase of a man's information involves, and is involved by,
| a corresponding increase of a word's information.
|
| Without fatiguing the reader by stretching this parallelism too far, it is
| sufficient to say that there is no element whatever of man's consciousness
| which has not something corresponding to it in the word; and the reason is
| obvious. It is that the word or sign which man uses *is* the man itself.
| For, as the fact that every thought is a sign, taken in conjunction with
| the fact that life is a train of thought, proves that man is a sign; so,
| that every thought is an *external* sign proves that man is an external
| sign. That is to say, the man and the external sign are identical, in
| the same sense in which the words 'homo' and 'man' are identical. Thus
| my language is the sum total of myself; for the man is the thought ...
|
|'Charles S. Peirce: Selected Writings (Values in a Universe of Chance)',
| edited with an introduction and notes by Philip P. Wiener, Dover,
| New York, NY, 1966. Originally published under the subtitle
| in parentheses above, Doubleday & Company, 1958.
I read you loud and clear.
Every manifold must have
its catalytic converter.
<Innumerate Continuation:>
TUC = The Usual CISPEC
TUC Alert:
| E.P.A. Says Catalytic Converter Is
| Growing Cause of Global Warming
| By Matthew L. Wald
| Copyright 1998 The New York Times
| May 29, 1998
| -----------------------------------------------------------------------
| WASHINGTON -- The catalytic converter, an invention that has sharply
| reduced smog from cars, has now become a significant and growing cause
| of global warming, according to the Environmental Protection Agency
Much as I would like to speculate ad libitum on these exciting new prospects for the
application of Peirce's chemico-algebraic theory of logic to the theorem-o-dynamics
of auto-semeiosis, I must get back to "business as usual" (BAU) ...
And now a word from our sponsor ...
http://www2.naias.com/
Reporting from Motown ---
Jon Awbrey
Discussion Note 22
HC = Howard Callaway
HC: You quote the following passage from a prior posting of mine:
HC: What remains relatively unclear is why we should need a system of notation
in which teridentity appears or is needed as against one in which it seems
not to be needed -- since assertion of identity can be made for any number
of terms in the standard predicate calculus.
HC: You comment as follows:
JA: This sort of statement totally non-plusses me.
It seems like a complete non-sequitur or even
a contradiction in terms to me.
JA: The question is about the minimal adequate resource base for
defining, deriving, or generating all of the concepts that we
need for a given but very general type of application that we
conventionally but equivocally refer to as "logic". You seem
to be saying something like this: We don't need 3-identity
because we have 4-identity, 5-identity, 6-identity, ..., in
the "standard predicate calculus". The question is not what
concepts are generated in all the generations that follow the
establishment of the conceptual resource base (axiom system),
but what is the minimal set of concepts that we can use to
generate the needed collection of concepts. And there the
answer is, in a way that is subject to the usual sorts of
mathematical proof, that 3-identity is the minimum while
2-identity is not big enough to do the job we want to do.
HC: I have fallen a bit behind on this thread while attending to some other
matters, but in this reply, you do seem to me to be coming around to an
understanding of the issues involved, as I see them. You put the matter
this way, "We don't need 3-identity because we have 4-identity, 5-identity,
6-identity, ..., in the 'standard predicate calculus'". Actually, as I think
you must know, there is no such thing as "4-identity", "5-identity", etc., in
the standard predicate calculus. It is more that such concepts are not needed,
just as teridentity is not needed, since the general apparatus of the predicate
calculus allows us to express identity among any number of terms without special
provision beyond "=".
No, that is not the case. Standard predicate calculus allows the expression
of predicates I_k, for k = 2, 3, 4, ..., such that I_k (x_1, ..., x_k) holds
if and only if all x_j, for j = 1 to k, are identical. So predicate calculus
contains a k-identity predicate for all such k. So whether "they're in there"
is not an issue. The question is whether these or any other predicates can be
constructed or defined in terms of 2-adic relations alone. And the answer is
no, they cannot. The vector of the misconception counterwise appears to be
as various a virus as the common cold, and every bit as resistant to cure.
I have taken the trouble to enumerate some of the more prevalent strains,
but most of them appear to go back to the 'Principia Mathematica', and
the variety of nominalism called "syntacticism" -- Ges-und-heit! --
that was spread by it, however unwittedly by some of its carriers.
Discussion Note 23
In trying to answer the rest of your last note, it seems that we cannot go any further without achieving some concrete clarity as to what is denominated by "standard predicate calculus", that is, "first order logic", or whatever. There is a "canonical" presentation of the subject, as I remember it, anyway, in the following sample of materials from Chang & Keisler's 'Model Theory'. (There's a newer edition of the book, but this part of the subject hasn't really changed all that much in ages.) Model Theory 01-39
Discussion Note 24
HC = Howard Callaway
HC: I might object that "teridentity" seems to come
to a matter of "a=b & b=c", so that a specific
predicate of teridentity seems unnecessary.
I am presently concerned with expositing and interpreting
the logical system that Peirce laid out in the LOR of 1870.
It is my considered opinion after thirty years of study that
there are untapped resources remaining in this work that have
yet to make it through the filters of that ilk of syntacticism
that was all the rage in the late great 1900's. I find there
to be an appreciably different point of view on logic that is
embodied in Peirce's work, and until we have made the minimal
effort to read what he wrote it is just plain futile to keep
on pretending that we have already assimilated it, or that
we are qualified to evaluate its cogency.
The symbol "&" that you employ above denotes a mathematical object that
qualifies as a 3-adic relation. Independently of my own views, there
is an abundance of statements in evidence that mathematical thinkers
from Peirce to Goedel consider the appreciation of facts like this
to mark the boundary between realism and nominalism in regard to
mathematical objects.
Discussion Note 25
HC = Howard Callaway
JA = Jon Awbrey
HC: I might object that "teridentity" seems to come
to a matter of "a=b & b=c", so that a specific
predicate of teridentity seems unnecessary.
JA: I am presently concerned with expositing and interpreting
the logical system that Peirce laid out in the LOR of 1870.
It is my considered opinion after thirty years of study that
there are untapped resources remaining in this work that have
yet to make it through the filters of that ilk of syntacticism
that was all the rage in the late great 1900's. I find there
to be an appreciably different point of view on logic that is
embodied in Peirce's work, and until we have made the minimal
effort to read what he wrote it is just plain futile to keep
on pretending that we have already assimilated it, or that
we are qualified to evaluate its cogency.
JA: The symbol "&" that you employ above denotes a mathematical object that
qualifies as a 3-adic relation. Independently of my own views, there
is an abundance of statements in evidence that mathematical thinkers
from Peirce to Goedel consider the appreciation of facts like this
to mark the boundary between realism and nominalism in regard to
mathematical objects.
HC: I would agree, I think, that "&" may be thought of
as a function mapping pairs of statements onto the
conjunction of that pair.
Yes, indeed, in the immortal words of my very first college algebra book:
"A binary operation is a ternary relation". As it happens, the symbol "&"
is equivocal in its interpretation -- computerese today steals a Freudian
line and dubs it "polymorphous" -- it can be regarded in various contexts
as a 3-adic relation on syntactic elements called "sentences", on logical
elements called "propositions", or on truth values collated in the boolean
domain B = {false, true} = {0, 1}. But the mappings and relations between
all of these interpretive choices are moderately well understood. Still,
no matter how many ways you enumerate for looking at a B-bird, the "&" is
always 3-adic. And that is sufficient to meet your objection, so I think
I will just leave it there until next time.
On a related note, that I must postpone until later:
We seem to congrue that there is a skewness between
the way that most mathematicians use logic and some
philosophers talk about logic, but I may not be the
one to set it adjoint, much as I am inclined to try.
At the moment I have this long-post-poned exponency
to carry out. I will simply recommend for your due
consideration Peirce's 1870 Logic Of Relatives, and
leave it at that. There's a cornucopiousness to it
that's yet to be dreamt of in the philosophy of the
1900's. I am doing what I can to infotain you with
the Gardens of Mathematical Recreations that I find
within Peirce's work, and that's in direct response
to many, okay, a couple of requests. Perhaps I can
not hope to attain the degree of horticultural arts
that Gardners before me have exhibited in this work,
but then again, who could? Everybody's a critic --
but the better ones read first, and criticize later.
Discussion Note 26
HC = Howard Callaway
HC: But on the other hand, it is not customary to think of "&" as
a relation among statements or sentences -- as, for instance,
logical implication is considered a logical relation between
statements or sentences.
Actually, it is the custom in many quarters to treat all of the
boolean operations, logical connectives, propositional relations,
or whatever you want to call them, as "equal citizens", having each
their "functional" (f : B^k -> B) and their "relational" (L c B^(k+1))
interpretations and applications. From this vantage, the interpretive
distinction that is commonly regarded as that between "assertion" and
mere "contemplation" is tantamount to a "pragmatic" difference between
computing the values of a function on a given domain of arguments and
computing the inverse of a function vis-a-vis a prospective true value.
This is the logical analogue of the way that our mathematical models
of reality have long been working, unsuspected and undisturbed by
most philosophers of science, I might add. If only the logical
side of the ledger were to be developed rather more fully than
it is at present, we might wake one of these days to find our
logical accounts of reality, finally, at long last, after an
overweaningly longish adolescence, beginning to come of age.
Discussion Note 27
HC = Howard Callaway
HC: For, if I make an assertion A&B, then I am not asserting
that the statement A stands in a relation to a statement B.
Instead, I am asserting the conjunction A&B (which logically
implies both the conjuncts in view of the definition of "&").
Please try to remember where we came in. This whole play of
animadversions about 3-adicity and 3-identity is set against
the backdrop of a single point, over the issue as to whether
3-adic relations are wholly dispensable or somehow essential
to logic, mathematics, and indeed to argument, communication,
and reasoning in general. Some folks clamor "Off with their
unnecessary heads!" -- other people, who are forced by their
occupations to pay close attention to the ongoing complexity
of the processes at stake, know that, far from finding 3-ads
in this or that isolated corner of the realm, one can hardly
do anything at all in the ways of logging or mathing without
running smack dab into veritable hosts of them.
I have just shown that "a=b & b=c" involves a 3-adic relation.
Some people would consider this particular 3-adic relation to
be more complex than the 3-identity relation, but that may be
a question of taste. At any rate, the 3-adic aspect persists.
HC: If "&" counts as a triadic relation, simply because it serves
to conjoin two statements into a third, then it would seem that
any binary relation 'R' will count as triadic, simply because
it places two things into a relation, which is a "third" thing.
By the same kind of reasoning a triadic relation, as ordinarily
understood would be really 4-adic.
The rest of your comments are just confused,
and do not use the terms as they are defined.
Discussion Note 28
JA = Jon Awbrey
JR = Joseph Ransdell
JA: Notice that Peirce follows the mathematician's usual practice,
then and now, of making the status of being an "individual" or
a "universal" relative to a discourse in progress. I have come
to appreciate more and more of late how radically different this
"patchwork" or "piecewise" approach to things is from the way of
some philosophers who seem to be content with nothing less than
many worlds domination, which means that they are never content
and rarely get started toward the solution of any real problem.
Just my observation, I hope you understand.
JR: Yes, I take this as underscoring and explicating the import of
making logic prior to rather than dependent upon metaphysics.
I think that Peirce, and of course many math folks, would take math
as prior, on a par, or even identical with logic. Myself I've been
of many minds about this over the years. The succinctest picture
that I get from Peirce is always this one:
| [Riddle of the Sphynx]
|
| Normative science rests largely on phenomenology and on mathematics;
| Metaphysics on phenomenology and on normative science.
|
| C.S. Peirce, CP 1.186 (1903)
|
|
| o Metaphysics
| /|
| / |
| / |
| Normative Science o |
| / \ |
| / \ |
| / \|
| Mathematics o o Phenomenology
|
|
| ROTS. http://stderr.org/pipermail/inquiry/2004-March/001262.html
Logic being a normative science must depend on math and phenomenology.
Of course, it all depends on what a person means by "logic" ...
JA: I also observe that Peirce takes the individual objects of
a particular universe of discourse in a "generative" way,
not a "totalizing" way, and thus they afford us with the
basis for talking freely about collections, constructions,
properties, qualities, subsets, and "higher types", as
the phrase is mint.
JR: Would this be essentially the same as regarding quantification as
distributive rather than collective, i.e. we take the individuals
of a class one-by-one as selectable rather than as somehow given
all at once, collectively?
Gosh, that's a harder question. Your suggestion reminds me
of the way that some intuitionist and even some finitist
mathematicians talk when they reflect on math practice.
I have leanings that way, but when I have tried to
give up the classical logic axioms, I have found
them too built in to my way of thinking to quit.
Still, a healthy circumspection about about our
often-wrongly vaunted capacties to conceive of
totalities is a habitual part of current math.
Again, I think individuals are made not born,
that is, to some degree factitious and mere
compromises of this or that conveniency.
This is one of the reasons that I have
been trying to work out the details
of a functional approach to logic,
propostional, quantificational,
and relational.
Cf: INTRO 30. http://stderr.org/pipermail/inquiry/2004-November/001765.html
In: INTRO. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1720
Discussion Note 29
JA = Jon Awbrey
GR = Gary Richmond
Re: LOR.COM 11.24. http://stderr.org/pipermail/inquiry/2004-November/001836.html
In: LOR.COM. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1755
JA: The manner in which these arrows and qualified arrows help us
to construct a suspension bridge that unifies logic, semiotics,
statistics, stochastics, and information theory will be one of
the main themes that I aim to elaborate throughout the rest of
this inquiry.
GR: Pretty ambitious, Jon. I'm sure you're up to it.
GR: I'd like to anticipate 3 versions: The mathematical (cactus diagrams, etc.),
the poetic, and the commonsensical -- ordinary language for those who are
NEITHER logicians NOR poets.
GR: Are you up to THAT?
Riddle A Body: "Time Enough, And Space, Excalibrate Co-Arthurs Should Apply"
Discussion Note 30
JA = Jon Awbrey GR = Gary Richmond Re: LOR.DIS 29. http://stderr.org/pipermail/inquiry/2004-November/001838.html In: LOR.DIS. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1768 JA: Riddle A Body: "Time Enough, And Space, Excalibrate Co-Arthurs Should Apply" GR: Well said, and truly! Body A Riddle: TEASE CASA = Fun House.
Discussion Note 31
Many illusions of selective reading -- like the myth that Peirce did not discover quantification over indices until 1885 -- can be dispelled by looking into his 1870 "Logic of Relatives". I started a web study of this in 2002, reworked again in 2003 and 2004, the current version of which can be found here: LOR. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1750 LOR-COM. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1755 LOR-DIS. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1768 I've only gotten as far as the bare infrastructure of Peirce's 1870 LOR, but an interesting feature of the study is that, if one draws the pictures that seem almost demanded by his way of linking up indices over expressions, then one can see a prototype of his much later logical graphs developing in the text.
Discussion Work Areas
Discussion Work Area 1
BM: Several discussions could take place there,
as to the reasons for the number of divisions,
the reasons of the titles themselves. Another
one is my translation from "normal interpretant"
into "final interpretant" (which one is called
elsewhere "Eventual Interpretant" or "Destinate
Interpretant" by CSP). I let all this aside
to focus on the following remark:
BM: 6 divisions correspond to individual correlates:
(S, O_i, O_d, I_i, I_d, I_n),
3 divisions correspond to dyads:
(S : O_d, S : I_d, S : I_n),
and the tenth to a triad:
(S : O_d : I_n).
This remark would itself deserve
a lot of explanations but one
more time I let this aside.
BM: Then we have the following very clear statement from Peirce:
| It follows from the Definition of a Sign
| that since the Dynamoid Object determines
| the Immediate Object,
| which determines the Sign,
| which determines the Destinate Interpretant
| which determines the Effective Interpretant
| which determines the Explicit Interpretant
|
| the six trichotomies, instead of determining 729 classes of signs,
| as they would if they were independent, only yield 28 classes; and
| if, as I strongly opine (not to say almost prove) there are four other
| trichotomies of signs of the same order of importance, instead of making
| 59049 classes, these will only come to 66.
|
| CSP, "Letter to Lady Welby", 14 Dec 1908, LW, p. 84.
BM: The separation made by CSP between 6 divisions and four others
seems to rely upon the suggested difference between individual
correlates and relations. We get the idea that the 10 divisions
are ordered on the whole and will end into 66 classes (by means of
three ordered modal values on each division: maybe, canbe, wouldbe).
Finally we have too the ordering for the divisions relative to the
correlates that I write in my notation:
Od -> Oi -> S -> If -> Id -> Ii.
BM: This order of "determinations" has bothered many people
but if we think of it as operative in semiosis, it seems
to be correct (at least to my eyes). Thus the question is:
where, how, and why the "four other trichotomies" fit in this
schema to obtain a linear ordering on the whole 10 divisions?
May be the question can be rephrased as: how intensional
relationships fit into an extensional one? Possibly the
question could be asked the other way. R. Marty responds
that in a certain sense the four trichotomies give nothing
more than the previous six ones but I strongly doubt of this.
BM: I put the problem in graphical form in an attached file
because my message editor will probably make some mistakes.
I make a distinction between arrow types drawing because I am
not sure that the sequence of correlates determinations is of
the same nature than correlates determination inside relations.
BM: It looks as if the problem amounts to some kind of projection
of relations on the horizontal axis made of correlates.
BM: If we consider some kind of equivalence (and this seems necessary to
obtain a linear ordering), by means of Agent -> Patient reductions on
relations, then erasing transitive determinations leads to:
Od -> Oi -> S -> S-Od -> If -> S-If -> S-Od-If -> Id -> S-Id -> Ii
BM: While it is interesting to compare the subsequence
S-Od -> If -> S-If -> S-Od-If with the pragmatic maxim,
I have no clear idea of the (in-) validity of such a result.
But I am convinced that the clarity has to come from the
Logic Of Relatives.
BM: I will be very grateful if you can make something with all that stuff.
Discussion Work Area 2
BM: I also found this passage which may be of some interest
(CP 4.540, Prolegomena to an Apology of Pragmatism):
| But though an Interpretant is not necessarily a Conclusion, yet a
| Conclusion is necessarily an Interpretant. So that if an Interpretant is
| not subject to the rules of Conclusions there is nothing monstrous in my
| thinking it is subject to some generalization of such rules. For any
| evolution of thought, whether it leads to a Conclusion or not, there is a
| certain normal course, which is to be determined by considerations not in
| the least psychological, and which I wish to expound in my next
| article;†1 and while I entirely agree, in opposition to distinguished
| logicians, that normality can be no criterion for what I call
| rationalistic reasoning, such as alone is admissible in science, yet it
| is precisely the criterion of instinctive or common-sense reasoning,
| which, within its own field, is much more trustworthy than rationalistic
| reasoning. In my opinion, it is self-control which makes any other than
| the normal course of thought possible, just as nothing else makes any
| other than the normal course of action possible; and just as it is
| precisely that that gives room for an ought-to-be of conduct, I mean
| Morality, so it equally gives room for an ought-to-be of thought, which
| is Right Reason; and where there is no self-control, nothing but the
| normal is possible. If your reflections have led you to a different
| conclusion from mine, I can still hope that when you come to read my next
| article, in which I shall endeavor to show what the forms of thought are,
| in general and in some detail, you may yet find that I have not missed
| the truth.
JA: Just as I have always feared, this classification mania
appears to be communicable! But now I must definitely
review the Welby correspondence, as all this stuff was
a blur to my sensibilities the last 10 times I read it.
BM: I think that I understand your reticence. I wonder if:
a. the fact that the letters to Lady Welby have been published as such,
has not lead to approach the matter in a certain way.
b. other sources, eventually unpublished, would give another lighting on
the subject, namely a logical one. I think of MS 339 for example that
seems to be part of the Logic Notebook. I have had access to some pages
of it, but not to the whole MS.
BM: A last remark. I don't think that classification is a mania for CSP but I
know that you know that! It is an instrument of thought and I think that
it is in this case much more a plan for experimenting than the exposition
of a conclusion. Experimenting what ? There is a strange statement in a
letter to W. James where CSP says that what is in question in his "second
way of dividing signs" is the logical theory of numbers. I give this from
memory. I have not the quote at hand now but I will search for it if needed.
Discussion Work Area 3
BM = Bernard Morand
JA = Jon Awbrey
JA: ... but now I have to add to my do-list the problems of comparing
the whole variorum of letters and drafts of letters to Lady Welby.
I only have the CP 8 and Wiener versions here, so I will depend
on you for ample excerpts from the Lieb volume.
BM: I made such a kind of comparison some time ago. I selected the following
3 cases on the criterium of alternate "grounds". Hoping it could save
some labor. The first rank expressions come from the MS 339 written in
Oct. 1904 and I label them with an (a). I think that it is interesting to
note that they were written four years before the letters to Welby and
just one or two years after the Syllabus which is the usual reference for
the classification in 3 trichotomies and 10 classes. The second (b) is
our initial table (from a draft to Lady Welby, Dec. 1908, CP 8.344) and
the third (c) comes from a letter sent in Dec. 1908 (CP 8.345-8.376). A
tabular presentation would be better but I can't do it. Comparing (c)
against (a) and (b) is informative, I think.
Division 1
(a) According to the matter of the Sign
(b) According to the Mode of Apprehension of the Sign itself
(c) Signs in respect to their Modes of possible Presentation
Division 2
(a) According to the Immediate Object
(b) According to the Mode of Presentation of the Immediate Object
(c) Objects, as they may be presented
Division 3
(a) According to the Matter of the Dynamic Object
(b) According to the Mode of Being of the Dynamical Object
(c) In respect to the Nature of the Dynamical Objects of Signs
Division 4
(a) According to the mode of representing object by the Dynamic Object
(b) According to the Relation of the Sign to its Dynamical Object
(c) The fourth Trichotomy
Division 5
(a) According to the Immédiate Interpretant
(b) According to the Mode of Presentation of the Immediate Interpretant
(c) As to the nature of the Immediate (or Felt ?) Interpretant
Division 6
(a) According to the Matter of Dynamic Interpretant
(b) According to the Mode of Being of the Dynamical Interpretant
(c) As to the Nature of the Dynamical Interpretant
Division 7
(a) According to the Mode of Affecting Dynamic Interpretant
(b) According to the relation of the Sign to the Dynamical Interpretant
(c) As to the Manner of Appeal to the Dynamic Interpretant
Division 8
(a) According to the Matter of Representative Interpretant
(b) According to the Nature of the Normal Interpretant
(c) According to the Purpose of the Eventual Interpretant
Division 9
(a) According to the Mode of being represented by Representative Interpretant
(b) According to the the relation of the Sign to the Normal Interpretant
(c) As to the Nature of the Influence of the Sign
Division 10
(a) According to the Mode of being represented to represent object by Sign, Truly
(b) According to the Triadic Relation of the Sign to its Dynamical Object and to
its Normal Interpretant
(c) As to the Nature of the Assurance of the Utterance
Discussion Work Area 4
JA: It may appear that one has side-stepped the issue of empiricism
that way, but then all that stuff about the synthetic a priori
raises its head, and we have Peirce's insight that mathematics
is observational and even experimental, and so I must trail off
into uncoordinated elliptical thoughts ...
HC: In contrast with this it strikes me that not all meanings of "analytic"
and "synthetic" have much, if anything, to do with the "analytic and the
synthetic", say, as in Quine's criticism of the "dualism" of empiricism.
Surely no one thinks that a plausible analysis must be analytic or that
synthetic materials tell us much about epistemology. So, it is not
clear that anything connected with analyticity or a priori knowledge
will plausibly or immediately arise from a discussion of analytical
geometry. Prevalent mathematical assumptions or postulates, yes --
but who says these are a prior? Can't non-Euclidean geometry also
be treated in the style of analytic geometry?
HC: I can imagine the a discussion might be forced in
that direction, but the connections don't strike me
as at all obvious or pressing. Perhaps Jon would just
like to bring up the notion of the synthetic apriori?
But why?
Discussion Work Area 5
HC = Howard Callaway
HC: But I see you as closer to my theme or challenge, when you say
"The question is about the minimal adequate resource base for
defining, deriving, or generating all of the concepts that we
need for a given but very general type of application that we
conventinally but equivocally refer to as 'logic'".
HC: I think it is accepted on all sides of the discussion that there
is some sort of "equivalence" between the standard predicate logic
and Peirce's graphs.
There you would be mistaken, except perhaps for the fact that
"some sort of equivalence" is vague to the depths of vacuity.
It most particularly does not mean "all sorts of equivalence"
or even "all important sorts of equivalence". It is usually
interpreted to mean an extremely abstract type of syntactic
equivalence, and that is undoubtedly one important type of
equivalence that it is worth examining whether two formal
systems have or not. But it precisely here that we find
another symptom of syntacticism, namely, the deprecation
of all other important qualities of formal systems, most
pointedly their "analystic, "semantic", and "pragmatic"
qualities, which make all the difference in how well the
system actually serves its users in a real world practice.
You can almost hear the whining and poohing coming from the
syntactic day camp, but those are the hard facts of the case.
HC: But we find this difference in relation to the vocabulary used to express
identity. From the point of view of starting with the predicate calculus,
we don't need "teridentity". So, this seems to suggest there is something
of interesting contrast in Peirce's logic, which brings in this concept.
The obvious question may be expressed by asking why we need teridentity
in Peirce's system and how Peirce's system may recommend itself in contrast
to the standard way with related concepts. This does seem to call for
a comparative evaluation of distinctive systems. That is not an easy task,
as I think we all understand. But I do think that if it is a goal to have
Peirce's system better appreciated, then that kind of question must be
addressed. If "=" is sufficient in the standard predicate calculus,
to say whatever we may need to say about the identity of terms, then
what is the advantage of an alternative system which insists on always
expressing identity of triples?
HC: The questions may look quite different, depending on where we start.
But in any case, I thought I saw some better appreciation of the
questions in your comments above.
Discussion Work Area 6
It's been that way for about as long as anybody can remember, and it will remain so, in spite of the spate of history rewriting and image re-engineering that has become the new rage in self-styled "analytic" circles.
Discussion Work Area 7
The brands of objection that you continue to make, with no evidence
of reflection on the many explanations that I and others have taken
the time to write out for you, lead me to believe that you are just
not interested in making that effort. That's okay, life is short,
the arts are long and many, there is always something else to do.
HC: For, if I make an assertion A&B, then I am not asserting
that the statement A stands in a relation to a statement B.
Instead, I am asserting the conjunction A&B (which logically
implies both the conjuncts in view of the definition of "&").
If "&" counts as a triadic relation, simply because it serves
to conjoin two statements into a third, then it would seem that
any binary relation 'R' will count as triadic, simply because
it places two things into a relation, which is a "third" thing.
By the same kind of reasoning a triadic relation, as ordinarily
understood would be really 4-adic.
HC: Now, I think this is the kind of argument you are making, ...
No, it's the kind of argument that you are making.
I am not making that kind of argument, and Peirce
did not make that kind of argument. Peirce used
his terms subject to definitions that would have
been understandable, and remain understandable,
to those of his readers who understand these
elementary definitions, either though their
prior acquaintance with standard concepts
or through their basic capacity to read
a well-formed, if novel definition.
Peirce made certain observations about the structure of logical concepts
and the structure of their referents. Those observations are accurate
and important. He expressed those observations in a form that is clear
to anybody who knows the meanings of the technical terms that he used,
and he is not responsible for the interpretations of those who don't.
HC: ... and it seems to both trivialize the claimed argument
for teridentity, by trivializing the conception of what
is to count as a triadic, as contrasted with a binary
relation, and it also seems to introduce a confusion
about what is is count as a binary, vs. a triadic
relation.
Yes, the argument that you are making trivializes
just about everything in sight, but that is the
common and well-known property of any argument
that fails to base itself on a grasp of the
first elements of the subject matter.
HC: If this is mathematical realism, then so much the worse for
mathematical realism. I am content to think that we do not
have a free hand in making up mathematical truth.
No, it's not mathematical realism. It is your reasoning,
and it exhibits all of the symptoms of syntacticism that
I have already diagnosed. It's a whole other culture
from what is pandemic in the practice of mathematics,
and it never fails to surprise me that people who
would never call themselves "relativists" in any
other matter of culture suddenly turn into just
that in matters of simple mathematical fact.
Document History
Ontology List (Dec 2002 – Feb 2003)
- http://suo.ieee.org/ontology/msg04416.html
- http://suo.ieee.org/ontology/msg04417.html
- http://suo.ieee.org/ontology/msg04418.html
- http://suo.ieee.org/ontology/msg04419.html
- http://suo.ieee.org/ontology/msg04421.html
- http://suo.ieee.org/ontology/msg04422.html
- http://suo.ieee.org/ontology/msg04423.html
- http://suo.ieee.org/ontology/msg04424.html
- http://suo.ieee.org/ontology/msg04425.html
- http://suo.ieee.org/ontology/msg04426.html
- http://suo.ieee.org/ontology/msg04427.html
- http://suo.ieee.org/ontology/msg04431.html
- http://suo.ieee.org/ontology/msg04432.html
- http://suo.ieee.org/ontology/msg04435.html
- http://suo.ieee.org/ontology/msg04436.html
- http://suo.ieee.org/ontology/msg04437.html
- http://suo.ieee.org/ontology/msg04438.html
- http://suo.ieee.org/ontology/msg04439.html
- http://suo.ieee.org/ontology/msg04440.html
- http://suo.ieee.org/ontology/msg04441.html
- http://suo.ieee.org/ontology/msg04442.html
- http://suo.ieee.org/ontology/msg04443.html
- http://suo.ieee.org/ontology/msg04444.html
- http://suo.ieee.org/ontology/msg04445.html
- http://suo.ieee.org/ontology/msg04446.html
- http://suo.ieee.org/ontology/msg04447.html
- http://suo.ieee.org/ontology/msg04448.html
- http://suo.ieee.org/ontology/msg04449.html
- http://suo.ieee.org/ontology/msg04450.html
- http://suo.ieee.org/ontology/msg04451.html
- http://suo.ieee.org/ontology/msg04452.html
- http://suo.ieee.org/ontology/msg04453.html
- http://suo.ieee.org/ontology/msg04454.html
- http://suo.ieee.org/ontology/msg04456.html
- http://suo.ieee.org/ontology/msg04457.html
- http://suo.ieee.org/ontology/msg04458.html
- http://suo.ieee.org/ontology/msg04459.html
- http://suo.ieee.org/ontology/msg04462.html
- http://suo.ieee.org/ontology/msg04464.html
- http://suo.ieee.org/ontology/msg04473.html
- http://suo.ieee.org/ontology/msg04478.html
- http://suo.ieee.org/ontology/msg04484.html
- http://suo.ieee.org/ontology/msg04487.html
- http://suo.ieee.org/ontology/msg04488.html
- http://suo.ieee.org/ontology/msg04492.html
- http://suo.ieee.org/ontology/msg04497.html
- http://suo.ieee.org/ontology/msg04498.html
- http://suo.ieee.org/ontology/msg04499.html
- http://suo.ieee.org/ontology/msg04500.html
- http://suo.ieee.org/ontology/msg04501.html
- http://suo.ieee.org/ontology/msg04502.html
- http://suo.ieee.org/ontology/msg04503.html
- http://suo.ieee.org/ontology/msg04504.html
- http://suo.ieee.org/ontology/msg04506.html
- http://suo.ieee.org/ontology/msg04508.html
- http://suo.ieee.org/ontology/msg04509.html
- http://suo.ieee.org/ontology/msg04510.html
- http://suo.ieee.org/ontology/msg04511.html
- http://suo.ieee.org/ontology/msg04512.html
- http://suo.ieee.org/ontology/msg04513.html
- http://suo.ieee.org/ontology/msg04516.html
- http://suo.ieee.org/ontology/msg04517.html
- http://suo.ieee.org/ontology/msg04518.html
- http://suo.ieee.org/ontology/msg04521.html
- http://suo.ieee.org/ontology/msg04539.html
- http://suo.ieee.org/ontology/msg04541.html
- http://suo.ieee.org/ontology/msg04542.html
- http://suo.ieee.org/ontology/msg04543.html
Ontology List : Discussion (Jan 2003)
- http://suo.ieee.org/ontology/msg04460.html
- http://suo.ieee.org/ontology/msg04461.html
- http://suo.ieee.org/ontology/msg04471.html
- http://suo.ieee.org/ontology/msg04472.html
- http://suo.ieee.org/ontology/msg04475.html
- http://suo.ieee.org/ontology/msg04476.html
- http://suo.ieee.org/ontology/msg04477.html
- http://suo.ieee.org/ontology/msg04479.html
- http://suo.ieee.org/ontology/msg04480.html
- http://suo.ieee.org/ontology/msg04481.html
- http://suo.ieee.org/ontology/msg04482.html
- http://suo.ieee.org/ontology/msg04483.html
- http://suo.ieee.org/ontology/msg04485.html
- http://suo.ieee.org/ontology/msg04486.html
- http://suo.ieee.org/ontology/msg04493.html
- http://suo.ieee.org/ontology/msg04494.html
- http://suo.ieee.org/ontology/msg04495.html
- http://suo.ieee.org/ontology/msg04496.html
Arisbe List (Jan–Feb 2003)
- http://stderr.org/pipermail/arisbe/2003-January/thread.html#1453
- http://stderr.org/pipermail/arisbe/2003-January/thread.html#1485
- http://stderr.org/pipermail/arisbe/2003-January/thread.html#1505
- http://stderr.org/pipermail/arisbe/2003-February/thread.html#1520
Arisbe List : Discussion (Jan 2003)
- http://stderr.org/pipermail/arisbe/2003-January/001455.html
- http://stderr.org/pipermail/arisbe/2003-January/001456.html
- http://stderr.org/pipermail/arisbe/2003-January/001458.html
- http://stderr.org/pipermail/arisbe/2003-January/001459.html
- http://stderr.org/pipermail/arisbe/2003-January/001460.html
- http://stderr.org/pipermail/arisbe/2003-January/001462.html
- http://stderr.org/pipermail/arisbe/2003-January/001463.html
- http://stderr.org/pipermail/arisbe/2003-January/001464.html
- http://stderr.org/pipermail/arisbe/2003-January/001465.html
- http://stderr.org/pipermail/arisbe/2003-January/001466.html
- http://stderr.org/pipermail/arisbe/2003-January/001468.html
- http://stderr.org/pipermail/arisbe/2003-January/001469.html
- http://stderr.org/pipermail/arisbe/2003-January/001476.html
- http://stderr.org/pipermail/arisbe/2003-January/001477.html
- http://stderr.org/pipermail/arisbe/2003-January/001478.html
- http://stderr.org/pipermail/arisbe/2003-January/001479.html
Inquiry List (Mar–Apr 2003)
- http://stderr.org/pipermail/inquiry/2003-March/thread.html#186
- http://stderr.org/pipermail/inquiry/2003-April/thread.html#245
- http://stderr.org/pipermail/inquiry/2003-March/000186.html
- http://stderr.org/pipermail/inquiry/2003-March/000187.html
- http://stderr.org/pipermail/inquiry/2003-March/000188.html
- http://stderr.org/pipermail/inquiry/2003-March/000189.html
- http://stderr.org/pipermail/inquiry/2003-March/000190.html
- http://stderr.org/pipermail/inquiry/2003-March/000191.html
- http://stderr.org/pipermail/inquiry/2003-March/000194.html
- http://stderr.org/pipermail/inquiry/2003-March/000195.html
- http://stderr.org/pipermail/inquiry/2003-April/000245.html
- http://stderr.org/pipermail/inquiry/2003-April/000246.html
- http://stderr.org/pipermail/inquiry/2003-April/000247.html
- http://stderr.org/pipermail/inquiry/2003-April/000248.html
- http://stderr.org/pipermail/inquiry/2003-April/000249.html
- http://stderr.org/pipermail/inquiry/2003-April/000250.html
- http://stderr.org/pipermail/inquiry/2003-April/000251.html
- http://stderr.org/pipermail/inquiry/2003-April/000252.html
- http://stderr.org/pipermail/inquiry/2003-April/000253.html
- http://stderr.org/pipermail/inquiry/2003-April/000254.html
- http://stderr.org/pipermail/inquiry/2003-April/000255.html
- http://stderr.org/pipermail/inquiry/2003-April/000256.html
- http://stderr.org/pipermail/inquiry/2003-April/000257.html
- http://stderr.org/pipermail/inquiry/2003-April/000258.html
- http://stderr.org/pipermail/inquiry/2003-April/000259.html
- http://stderr.org/pipermail/inquiry/2003-April/000260.html
- http://stderr.org/pipermail/inquiry/2003-April/000261.html
- http://stderr.org/pipermail/inquiry/2003-April/000262.html
- http://stderr.org/pipermail/inquiry/2003-April/000263.html
- http://stderr.org/pipermail/inquiry/2003-April/000264.html
- http://stderr.org/pipermail/inquiry/2003-April/000265.html
- http://stderr.org/pipermail/inquiry/2003-April/000267.html
- http://stderr.org/pipermail/inquiry/2003-April/000268.html
- http://stderr.org/pipermail/inquiry/2003-April/000269.html
- http://stderr.org/pipermail/inquiry/2003-April/000270.html
- http://stderr.org/pipermail/inquiry/2003-April/000271.html
- http://stderr.org/pipermail/inquiry/2003-April/000273.html
- http://stderr.org/pipermail/inquiry/2003-April/000274.html
- http://stderr.org/pipermail/inquiry/2003-April/000275.html
- http://stderr.org/pipermail/inquiry/2003-April/000276.html
- http://stderr.org/pipermail/inquiry/2003-April/000277.html
- http://stderr.org/pipermail/inquiry/2003-April/000278.html
- http://stderr.org/pipermail/inquiry/2003-April/000279.html
- http://stderr.org/pipermail/inquiry/2003-April/000280.html
- http://stderr.org/pipermail/inquiry/2003-April/000281.html
- http://stderr.org/pipermail/inquiry/2003-April/000282.html
- http://stderr.org/pipermail/inquiry/2003-April/000283.html
- http://stderr.org/pipermail/inquiry/2003-April/000284.html
- http://stderr.org/pipermail/inquiry/2003-April/000285.html
- http://stderr.org/pipermail/inquiry/2003-April/000286.html
- http://stderr.org/pipermail/inquiry/2003-April/000287.html
- http://stderr.org/pipermail/inquiry/2003-April/000288.html
- http://stderr.org/pipermail/inquiry/2003-April/000289.html
- http://stderr.org/pipermail/inquiry/2003-April/000290.html
- http://stderr.org/pipermail/inquiry/2003-April/000291.html
- http://stderr.org/pipermail/inquiry/2003-April/000294.html
- http://stderr.org/pipermail/inquiry/2003-April/000295.html
- http://stderr.org/pipermail/inquiry/2003-April/000296.html
- http://stderr.org/pipermail/inquiry/2003-April/000297.html
- http://stderr.org/pipermail/inquiry/2003-April/000298.html
- http://stderr.org/pipermail/inquiry/2003-April/000299.html
- http://stderr.org/pipermail/inquiry/2003-April/000300.html
- http://stderr.org/pipermail/inquiry/2003-April/000301.html
- http://stderr.org/pipermail/inquiry/2003-April/000302.html
- http://stderr.org/pipermail/inquiry/2003-April/000303.html
- http://stderr.org/pipermail/inquiry/2003-April/000305.html
- http://stderr.org/pipermail/inquiry/2003-April/000306.html
- http://stderr.org/pipermail/inquiry/2003-April/000307.html
- http://stderr.org/pipermail/inquiry/2003-April/000308.html
- http://stderr.org/pipermail/inquiry/2003-April/000309.html
Inquiry List : Selections (Nov 2004)
- http://stderr.org/pipermail/inquiry/2004-November/001750.html
- http://stderr.org/pipermail/inquiry/2004-November/001751.html
- http://stderr.org/pipermail/inquiry/2004-November/001752.html
- http://stderr.org/pipermail/inquiry/2004-November/001753.html
- http://stderr.org/pipermail/inquiry/2004-November/001754.html
- http://stderr.org/pipermail/inquiry/2004-November/001760.html
- http://stderr.org/pipermail/inquiry/2004-November/001769.html
- http://stderr.org/pipermail/inquiry/2004-November/001774.html
- http://stderr.org/pipermail/inquiry/2004-November/001783.html
- http://stderr.org/pipermail/inquiry/2004-November/001794.html
- http://stderr.org/pipermail/inquiry/2004-November/001812.html
- http://stderr.org/pipermail/inquiry/2004-November/001842.html
Inquiry List : Commentary (Nov 2004)
Inquiry List : Discussion (Nov 2004, Jan 2005, Apr 2009)
- http://stderr.org/pipermail/inquiry/2004-November/thread.html#1768
- http://stderr.org/pipermail/inquiry/2005-January/thread.html#2301
- http://stderr.org/pipermail/inquiry/2009-April/thread.html#3548
- http://stderr.org/pipermail/inquiry/2004-November/001768.html
- http://stderr.org/pipermail/inquiry/2004-November/001838.html
- http://stderr.org/pipermail/inquiry/2004-November/001840.html
- http://stderr.org/pipermail/inquiry/2005-January/002301.html
- http://stderr.org/pipermail/inquiry/2009-April/003548.html
- Artificial Intelligence
- Boolean Algebra
- Boolean Functions
- Charles Sanders Peirce
- Combinatorics
- Computational Complexity
- Computer Science
- Cybernetics
- Differential Logic
- Equational Reasoning
- Formal Languages
- Formal Systems
- Graph Theory
- Inquiry
- Inquiry Driven Systems
- Knowledge Representation
- Logic
- Logical Graphs
- Mathematics
- Philosophy
- Propositional Calculus
- Semiotics
- Visualization