Difference between revisions of "Minimal negation operator"
Jon Awbrey (talk | contribs) (→Truth tables: Table Heading (style="background:#f0f0ff) = Light Gray Blue) |
Jon Awbrey (talk | contribs) (→Charts and graphs: HTML → TeX + some clarification) |
||
| Line 142: | Line 142: | ||
==Charts and graphs== | ==Charts and graphs== | ||
| − | Two | + | Two ways of visualizing the space <math>\mathbb{B}^k</math> of <math>2^k\!</math> points are the [[hypercube]] picture and the [[venn diagram]] picture. The hypercube picture represents each point of <math>\mathbb{B}^k</math> by the corresponding point of the <math>k\!</math>-cube. The venn diagram picture represents each point of <math>\mathbb{B}^k</math> by the corresponding "cell" of the venn diagram on <math>k\!</math> "circles". |
In addition, each point of '''B'''<sup>k</sup> is the unique point in the '''[[fiber (mathematics)|fiber]] of truth''' <math>[|s|]</math> of a '''singular proposition''' ''s'' : '''B'''<sup>''k''</sup> → '''B''', and thus it is the unique point where a '''singular conjunction''' of ''k'' '''literals''' is 1. | In addition, each point of '''B'''<sup>k</sup> is the unique point in the '''[[fiber (mathematics)|fiber]] of truth''' <math>[|s|]</math> of a '''singular proposition''' ''s'' : '''B'''<sup>''k''</sup> → '''B''', and thus it is the unique point where a '''singular conjunction''' of ''k'' '''literals''' is 1. | ||
Revision as of 20:58, 20 May 2009
In logic and mathematics, the minimal negation operator \(\nu\!\) is a multigrade operator \((\nu_k)_{k \in \mathbb{N}}\) where each \(\nu_k\!\) is a \(k\!\)-ary boolean function defined in such a way that \(\nu_k (x_1, \ldots , x_k) = 1\) if and only if exactly one of the arguments \(x_j\!\) is \(0.\!\)
In contexts where the initial letter \(\nu\!\) is understood, the minimal negation operators can be indicated by argument lists in parentheses. The first four members of this family of operators are shown below, with paraphrases in a couple of other notations, where tildes and primes, respectively, indicate logical negation.
|
\(\begin{matrix} (~) & = & 0 & = & \operatorname{false} \'"`UNIQ-MathJax1-QINU`"' * The point \((0, 0, \ldots , 0, 0)\) with all 0's as coordinates is the point where the conjunction of all negated variables evaluates to 1, namely, the point where:
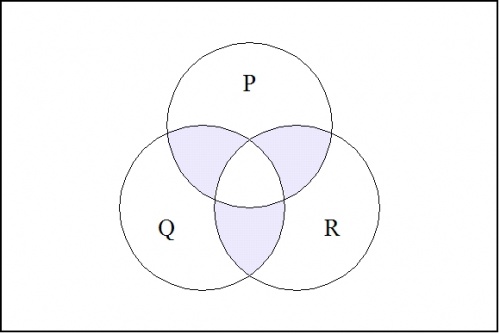
To pass from these limiting examples to the general case, observe that a singular proposition s : Bk → B can be given canonical expression as a conjunction of literals, \(s = e_1 e_2 \ldots e_{k-1} e_k\). Then the proposition \(\nu (e_1, e_2, \ldots, e_{k-1}, e_k)\) is 1 on the points adjacent to the point where s is 1, and 0 everywhere else on the cube. For example, consider the case where k = 3. Then the minimal negation operation \(\nu (p, q, r)\!\), when there is no risk of confusion written more simply as \((p, q, r)\!\), has the following venn diagram:
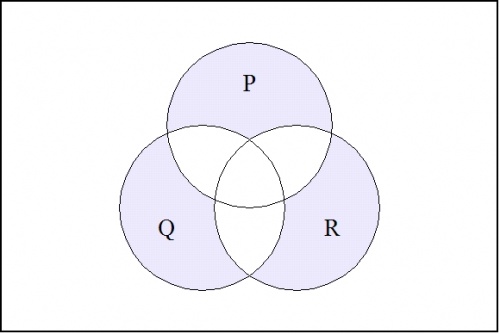
For a contrasting example, the boolean function expressed by the form \(((p),(q),(r))\!\) has the following venn diagram:
Glossary of basic terms
See alsoTemplate:Col-break
External linksAficionados
<sharethis /> |