Difference between revisions of "Minimal negation operator"
Jon Awbrey (talk | contribs) |
Jon Awbrey (talk | contribs) (typos) |
||
| Line 19: | Line 19: | ||
\\[6pt] | \\[6pt] | ||
\texttt{(x, y)} | \texttt{(x, y)} | ||
| − | & = & \ | + | & = & \nu_2 (x, y) |
& = & \tilde{x}y \lor x\tilde{y} | & = & \tilde{x}y \lor x\tilde{y} | ||
& = & x^\prime y \lor x y^\prime | & = & x^\prime y \lor x y^\prime | ||
\\[6pt] | \\[6pt] | ||
\texttt{(x, y, z)} | \texttt{(x, y, z)} | ||
| − | & = & \ | + | & = & \nu_3 (x, y, z) |
& = & \tilde{x}yz \lor x\tilde{y}z \lor xy\tilde{z} | & = & \tilde{x}yz \lor x\tilde{y}z \lor xy\tilde{z} | ||
& = & x^\prime y z \lor x y^\prime z \lor x y z^\prime | & = & x^\prime y z \lor x y^\prime z \lor x y z^\prime | ||
Revision as of 13:18, 24 August 2009
The minimal negation operator \(\nu\!\) is a multigrade operator \((\nu_k)_{k \in \mathbb{N}}\) where each \(\nu_k\!\) is a \(k\!\)-ary boolean function defined in such a way that \(\nu_k (x_1, \ldots , x_k) = 1\) in just those cases where exactly one of the arguments \(x_j\!\) is \(0.\!\)
In contexts where the initial letter \(\nu\!\) is understood, the minimal negation operators can be indicated by argument lists in parentheses. In the following text a distinctive typeface will be used for logical expressions based on minimal negation operators, for example, \(\texttt{(x, y, z)}\) = \(\nu (x, y, z).\!\)
The first four members of this family of operators are shown below, with paraphrases in a couple of other notations, where tildes and primes, respectively, indicate logical negation.
|
\(\begin{matrix} \texttt{()} & = & \nu_0 & = & 0 & = & \operatorname{false} \'"`UNIQ-MathJax1-QINU`"' * The point \((0, 0, \ldots , 0, 0)\) with all 0's as coordinates is the point where the conjunction of all negated variables evaluates to \(1,\!\) namely, the point where:
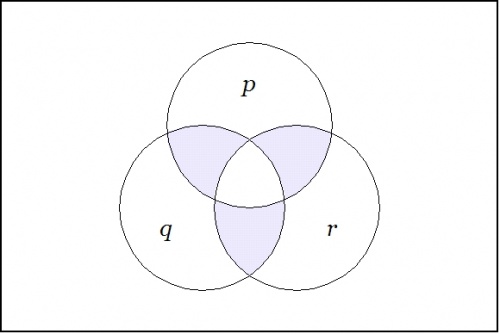
To pass from these limiting examples to the general case, observe that a singular proposition \(s : \mathbb{B}^k \to \mathbb{B}\) can be given canonical expression as a conjunction of literals, \(s = e_1 e_2 \ldots e_{k-1} e_k\). Then the proposition \(\nu (e_1, e_2, \ldots, e_{k-1}, e_k)\) is \(1\!\) on the points adjacent to the point where \(s\!\) is \(1,\!\) and 0 everywhere else on the cube. For example, consider the case where \(k = 3.\!\) Then the minimal negation operation \(\nu (p, q, r)\!\) — written more simply as \(\texttt{(p, q, r)}\) — has the following venn diagram:
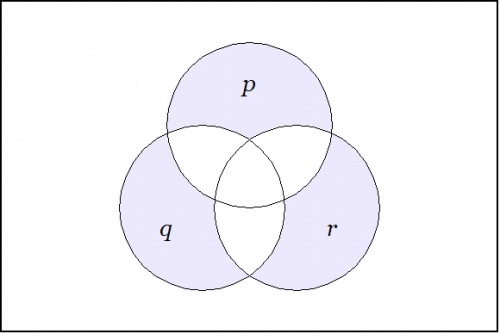
For a contrasting example, the boolean function expressed by the form \(\texttt{((p),(q),(r))}\) has the following venn diagram:
Glossary of basic terms
See alsoTemplate:Col-break
External links
|