|
\(\begin{matrix}
\mathrm{G}
& = & \mathrm{e}:\mathrm{e}
& + & \mathrm{f}:\mathrm{f}
& + & \mathrm{g}:\mathrm{g}
& + & \mathrm{h}:\mathrm{h}
\'"`UNIQ-MathJax2-QINU`"' is the relate, \(j\!\) is the correlate, and in our current example \(i\!:\!j,\!\) or more exactly, \(m_{ij} = 1,\!\) is taken to say that \(i\!\) is a marker for \(j.\!\) This is the mode of reading that we call “multiplying on the left”.
In the algebraic, permutational, or transformational contexts of application, however, Peirce converts to the alternative mode of reading, although still calling \(i\!\) the relate and \(j\!\) the correlate, the elementary relative \(i\!:\!j\!\) now means that \(i\!\) gets changed into \(j.\!\) In this scheme of reading, the transformation \(a\!:\!b + b\!:\!c + c\!:\!a\!\) is a permutation of the aggregate \(\mathbf{1} = a + b + c,\!\) or what we would now call the set \(\{ a, b, c \},\!\) in particular, it is the permutation that is otherwise notated as follows:
|
\(\begin{Bmatrix}
a & b & c
\\
b & c & a
\end{Bmatrix}\!\)
|
This is consistent with the convention that Peirce uses in the paper “On a Class of Multiple Algebras” (CP 3.324–327).
We've been exploring the applications of a certain technique for clarifying abstruse concepts, a rough-cut version of the pragmatic maxim that I've been accustomed to refer to as the operationalization of ideas. The basic idea is to replace the question of What it is, which modest people comprehend is far beyond their powers to answer definitively any time soon, with the question of What it does, which most people know at least a modicum about.
In the case of regular representations of groups we found a non-plussing surplus of answers to sort our way through. So let us track back one more time to see if we can learn any lessons that might carry over to more realistic cases.
Here is is the operation table of \(V_4\!\) once again:
\(\text{Klein Four-Group}~ V_4\!\)
|
\(\cdot\!\)
|
\(\mathrm{e}\!\)
|
\(\mathrm{f}\!\)
|
\(\mathrm{g}\!\)
|
\(\mathrm{h}\!\)
|
| \(\mathrm{e}\!\)
|
\(\mathrm{e}\!\)
|
\(\mathrm{f}\!\)
|
\(\mathrm{g}\!\)
|
\(\mathrm{h}\!\)
|
| \(\mathrm{f}\!\)
|
\(\mathrm{f}\!\)
|
\(\mathrm{e}\!\)
|
\(\mathrm{h}\!\)
|
\(\mathrm{g}\!\)
|
| \(\mathrm{g}\!\)
|
\(\mathrm{g}\!\)
|
\(\mathrm{h}\!\)
|
\(\mathrm{e}\!\)
|
\(\mathrm{f}\!\)
|
| \(\mathrm{h}\!\)
|
\(\mathrm{h}\!\)
|
\(\mathrm{g}\!\)
|
\(\mathrm{f}\!\)
|
\(\mathrm{e}\!\)
|
A group operation table is really just a device for recording a certain 3-adic relation, to be specific, the set of triples of the form \((x, y, z)\!\) satisfying the equation \(x \cdot y = z.\!\)
In the case of \(V_4 = (G, \cdot),\!\) where \(G\!\) is the underlying set \(\{ \mathrm{e}, \mathrm{f}, \mathrm{g}, \mathrm{h} \},\!\) we have the 3-adic relation \(L(V_4) \subseteq G \times G \times G\!\) whose triples are listed below:
|
\(\begin{matrix}
(\mathrm{e}, \mathrm{e}, \mathrm{e}) &
(\mathrm{e}, \mathrm{f}, \mathrm{f}) &
(\mathrm{e}, \mathrm{g}, \mathrm{g}) &
(\mathrm{e}, \mathrm{h}, \mathrm{h})
\\[6pt]
(\mathrm{f}, \mathrm{e}, \mathrm{f}) &
(\mathrm{f}, \mathrm{f}, \mathrm{e}) &
(\mathrm{f}, \mathrm{g}, \mathrm{h}) &
(\mathrm{f}, \mathrm{h}, \mathrm{g})
\\[6pt]
(\mathrm{g}, \mathrm{e}, \mathrm{g}) &
(\mathrm{g}, \mathrm{f}, \mathrm{h}) &
(\mathrm{g}, \mathrm{g}, \mathrm{e}) &
(\mathrm{g}, \mathrm{h}, \mathrm{f})
\\[6pt]
(\mathrm{h}, \mathrm{e}, \mathrm{h}) &
(\mathrm{h}, \mathrm{f}, \mathrm{g}) &
(\mathrm{h}, \mathrm{g}, \mathrm{f}) &
(\mathrm{h}, \mathrm{h}, \mathrm{e})
\end{matrix}\!\)
|
It is part of the definition of a group that the 3-adic relation \(L \subseteq G^3\!\) is actually a function \(L : G \times G \to G.\!\) It is from this functional perspective that we can see an easy way to derive the two regular representations. Since we have a function of the type \(L : G \times G \to G,\!\) we can define a couple of substitution operators:
| 1.
|
\(\mathrm{Sub}(x, (\underline{~~}, y))\!\) puts any specified \(x\!\) into the empty slot of the rheme \((\underline{~~}, y),\!\) with the effect of producing the saturated rheme \((x, y)\!\) that evaluates to \(xy.~\!\)
|
| 2.
|
\(\mathrm{Sub}(x, (y, \underline{~~}))\!\) puts any specified \(x\!\) into the empty slot of the rheme \((y, \underline{~~}),\!\) with the effect of producing the saturated rheme \((y, x)\!\) that evaluates to \(yx.~\!\)
|
In (1) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((\underline{~~}, y),\!\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((\underline{~~}, y)\!\) into \(xy,\!\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : xy) ~|~ y \in G \}.\!\) The pairs \((y : xy)\!\) can be found by picking an \(x\!\) from the left margin of the group operation table and considering its effects on each \(y\!\) in turn as these run across the top margin. This aspect of pragmatic definition we recognize as the regular ante-representation:
|
\(\begin{matrix}
\mathrm{e}
& = & \mathrm{e}\!:\!\mathrm{e}
& + & \mathrm{f}\!:\!\mathrm{f}
& + & \mathrm{g}\!:\!\mathrm{g}
& + & \mathrm{h}\!:\!\mathrm{h}
\\[4pt]
\mathrm{f}
& = & \mathrm{e}\!:\!\mathrm{f}
& + & \mathrm{f}\!:\!\mathrm{e}
& + & \mathrm{g}\!:\!\mathrm{h}
& + & \mathrm{h}\!:\!\mathrm{g}
\\[4pt]
\mathrm{g}
& = & \mathrm{e}\!:\!\mathrm{g}
& + & \mathrm{f}\!:\!\mathrm{h}
& + & \mathrm{g}\!:\!\mathrm{e}
& + & \mathrm{h}\!:\!\mathrm{f}
\\[4pt]
\mathrm{h}
& = & \mathrm{e}\!:\!\mathrm{h}
& + & \mathrm{f}\!:\!\mathrm{g}
& + & \mathrm{g}\!:\!\mathrm{f}
& + & \mathrm{h}\!:\!\mathrm{e}
\end{matrix}\!\)
|
In (2) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((y, \underline{~~}),\!\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((y, \underline{~~})\!\) into \(yx,\!\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : yx) ~|~ y \in G \}.\!\) The pairs \((y : yx)\!\) can be found by picking an \(x\!\) from the top margin of the group operation table and considering its effects on each \(y\!\) in turn as these run down the left margin. This aspect of pragmatic definition we recognize as the regular post-representation:
|
\(\begin{matrix}
\mathrm{e}
& = & \mathrm{e}\!:\!\mathrm{e}
& + & \mathrm{f}\!:\!\mathrm{f}
& + & \mathrm{g}\!:\!\mathrm{g}
& + & \mathrm{h}\!:\!\mathrm{h}
\\[4pt]
\mathrm{f}
& = & \mathrm{e}\!:\!\mathrm{f}
& + & \mathrm{f}\!:\!\mathrm{e}
& + & \mathrm{g}\!:\!\mathrm{h}
& + & \mathrm{h}\!:\!\mathrm{g}
\\[4pt]
\mathrm{g}
& = & \mathrm{e}\!:\!\mathrm{g}
& + & \mathrm{f}\!:\!\mathrm{h}
& + & \mathrm{g}\!:\!\mathrm{e}
& + & \mathrm{h}\!:\!\mathrm{f}
\\[4pt]
\mathrm{h}
& = & \mathrm{e}\!:\!\mathrm{h}
& + & \mathrm{f}\!:\!\mathrm{g}
& + & \mathrm{g}\!:\!\mathrm{f}
& + & \mathrm{h}\!:\!\mathrm{e}
\end{matrix}\!\)
|
If the ante-rep looks the same as the post-rep, now that I'm writing them in the same dialect, that is because \(V_4\!\) is abelian (commutative), and so the two representations have the very same effects on each point of their bearing.
So long as we're in the neighborhood, we might as well take in some more of the sights, for instance, the smallest example of a non-abelian (non-commutative) group. This is a group of six elements, say, \(G = \{ \mathrm{e}, \mathrm{f}, \mathrm{g}, \mathrm{h}, \mathrm{i}, \mathrm{j} \},\!\) with no relation to any other employment of these six symbols being implied, of course, and it can be most easily represented as the permutation group on a set of three letters, say, \(X = \{ a, b, c \},\!\) usually notated as \(G = \mathrm{Sym}(X)\!\) or more abstractly and briefly, as \(\mathrm{Sym}(3)\!\) or \(S_3.\!\) The next Table shows the intended correspondence between abstract group elements and the permutation or substitution operations in \(\mathrm{Sym}(X).\!\)
\(\text{Permutation Substitutions in}~ \mathrm{Sym} \{ a, b, c \}\!\)
| \(\mathrm{e}\!\)
|
\(\mathrm{f}\!\)
|
\(\mathrm{g}\!\)
|
\(\mathrm{h}\!\)
|
\(\mathrm{i}~\!\)
|
\(\mathrm{j}\!\)
|
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
a & b & c
\end{matrix}\!\)
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
c & a & b
\end{matrix}\!\)
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
b & c & a
\end{matrix}\!\)
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
a & c & b
\end{matrix}\!\)
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
c & b & a
\end{matrix}\!\)
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
b & a & c
\end{matrix}\!\)
|
Here is the operation table for \(S_3,\!\) given in abstract fashion:
| \(\text{Symmetric Group}~ S_3\!\)
|
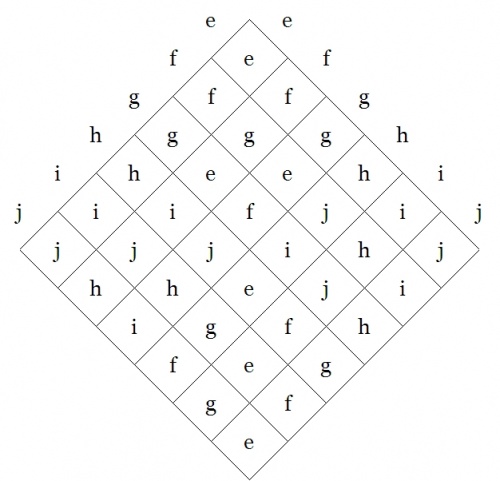
|
By the way, we will meet with the symmetric group \(S_3~\!\) again when we return to take up the study of Peirce's early paper “On a Class of Multiple Algebras” (CP 3.324–327), and also his late unpublished work “The Simplest Mathematics” (1902) (CP 4.227–323), with particular reference to the section that treats of “Trichotomic Mathematics” (CP 4.307–323).
By way of collecting a short-term pay-off for all the work that we did on the regular representations of the Klein 4-group \(V_4,\!\) let us write out as quickly as possible in relative form a minimal budget of representations for the symmetric group on three letters, \(\mathrm{Sym}(3).\!\) After doing the usual bit of compare and contrast among the various representations, we will have enough concrete material beneath our abstract belts to tackle a few of the presently obscured details of Peirce's early “Algebra + Logic” papers.
Writing the permutations or substitutions of \(\mathrm{Sym} \{ a, b, c \}\!\) in relative form generates what is generally thought of as a natural representation of \(S_3.~\!\)
|
\(\begin{matrix}
\mathrm{e}
& = & a\!:\!a
& + & b\!:\!b
& + & c\!:\!c
\\[4pt]
\mathrm{f}
& = & a\!:\!c
& + & b\!:\!a
& + & c\!:\!b
\\[4pt]
\mathrm{g}
& = & a\!:\!b
& + & b\!:\!c
& + & c\!:\!a
\\[4pt]
\mathrm{h}
& = & a\!:\!a
& + & b\!:\!c
& + & c\!:\!b
\\[4pt]
\mathrm{i}
& = & a\!:\!c
& + & b\!:\!b
& + & c\!:\!a
\\[4pt]
\mathrm{j}
& = & a\!:\!b
& + & b\!:\!a
& + & c\!:\!c
\end{matrix}\!\)
|
I have without stopping to think about it written out this natural representation of \(S_3~\!\) in the style that comes most naturally to me, to wit, the “right” way, whereby an ordered pair configured as \(x\!:\!y\!\) constitutes the turning of \(x\!\) into \(y.\!\) It is possible that the next time we check in with CSP we will have to adjust our sense of direction, but that will be an easy enough bridge to cross when we come to it.
To construct the regular representations of \(S_3,~\!\) we begin with the data of its operation table:
| \(\text{Symmetric Group}~ S_3\!\)
|

|
Just by way of staying clear about what we are doing, let's return to the recipe that we worked out before:
It is part of the definition of a group that the 3-adic relation \(L \subseteq G^3\!\) is actually a function \(L : G \times G \to G.\!\) It is from this functional perspective that we can see an easy way to derive the two regular representations.
Since we have a function of the type \(L : G \times G \to G,\!\) we can define a couple of substitution operators:
| 1.
|
\(\mathrm{Sub}(x, (\underline{~~}, y))\!\) puts any specified \(x\!\) into the empty slot of the rheme \((\underline{~~}, y),\!\) with the effect of producing the saturated rheme \((x, y)\!\) that evaluates to \(xy.~\!\)
|
| 2.
|
\(\mathrm{Sub}(x, (y, \underline{~~}))\!\) puts any specified \(x\!\) into the empty slot of the rheme \((y, \underline{~~}),\!\) with the effect of producing the saturated rheme \((y, x)\!\) that evaluates to \(yx.~\!\)
|
In (1) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((\underline{~~}, y),\!\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((\underline{~~}, y)\!\) into \(xy,\!\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : xy) ~|~ y \in G \}.\!\) The pairs \((y : xy)\!\) can be found by picking an \(x\!\) from the left margin of the group operation table and considering its effects on each \(y\!\) in turn as these run along the right margin. This produces the regular ante-representation of \(S_3,\!\) like so:
|
\(\begin{array}{*{13}{c}}
\mathrm{e}
& = & \mathrm{e}\!:\!\mathrm{e}
& + & \mathrm{f}\!:\!\mathrm{f}
& + & \mathrm{g}\!:\!\mathrm{g}
& + & \mathrm{h}\!:\!\mathrm{h}
& + & \mathrm{i}\!:\!\mathrm{i}
& + & \mathrm{j}\!:\!\mathrm{j}
\\[4pt]
\mathrm{f}
& = & \mathrm{e}\!:\!\mathrm{f}
& + & \mathrm{f}\!:\!\mathrm{g}
& + & \mathrm{g}\!:\!\mathrm{e}
& + & \mathrm{h}\!:\!\mathrm{j}
& + & \mathrm{i}\!:\!\mathrm{h}
& + & \mathrm{j}\!:\!\mathrm{i}
\\[4pt]
\mathrm{g}
& = & \mathrm{e}\!:\!\mathrm{g}
& + & \mathrm{f}\!:\!\mathrm{e}
& + & \mathrm{g}\!:\!\mathrm{f}
& + & \mathrm{h}\!:\!\mathrm{i}
& + & \mathrm{i}\!:\!\mathrm{j}
& + & \mathrm{j}\!:\!\mathrm{h}
\\[4pt]
\mathrm{h}
& = & \mathrm{e}\!:\!\mathrm{h}
& + & \mathrm{f}\!:\!\mathrm{i}
& + & \mathrm{g}\!:\!\mathrm{j}
& + & \mathrm{h}\!:\!\mathrm{e}
& + & \mathrm{i}\!:\!\mathrm{f}
& + & \mathrm{j}\!:\!\mathrm{g}
\\[4pt]
\mathrm{i}
& = & \mathrm{e}\!:\!\mathrm{i}
& + & \mathrm{f}\!:\!\mathrm{j}
& + & \mathrm{g}\!:\!\mathrm{h}
& + & \mathrm{h}\!:\!\mathrm{g}
& + & \mathrm{i}\!:\!\mathrm{e}
& + & \mathrm{j}\!:\!\mathrm{f}
\\[4pt]
\mathrm{j}
& = & \mathrm{e}\!:\!\mathrm{j}
& + & \mathrm{f}\!:\!\mathrm{h}
& + & \mathrm{g}\!:\!\mathrm{i}
& + & \mathrm{h}\!:\!\mathrm{f}
& + & \mathrm{i}\!:\!\mathrm{g}
& + & \mathrm{j}\!:\!\mathrm{e}
\end{array}\!\)
|
In (2) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((y, \underline{~~}),\!\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((y, \underline{~~})\!\) into \(yx,\!\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : yx) ~|~ y \in G \}.\!\) The pairs \((y : yx)\!\) can be found by picking an \(x\!\) on the right margin of the group operation table and considering its effects on each \(y\!\) in turn as these run along the left margin. This produces the regular post-representation of \(S_3,\!\) like so:
|
\(\begin{array}{*{13}{c}}
\mathrm{e}
& = & \mathrm{e}\!:\!\mathrm{e}
& + & \mathrm{f}\!:\!\mathrm{f}
& + & \mathrm{g}\!:\!\mathrm{g}
& + & \mathrm{h}\!:\!\mathrm{h}
& + & \mathrm{i}\!:\!\mathrm{i}
& + & \mathrm{j}\!:\!\mathrm{j}
\\[4pt]
\mathrm{f}
& = & \mathrm{e}\!:\!\mathrm{f}
& + & \mathrm{f}\!:\!\mathrm{g}
& + & \mathrm{g}\!:\!\mathrm{e}
& + & \mathrm{h}\!:\!\mathrm{i}
& + & \mathrm{i}\!:\!\mathrm{j}
& + & \mathrm{j}\!:\!\mathrm{h}
\\[4pt]
\mathrm{g}
& = & \mathrm{e}\!:\!\mathrm{g}
& + & \mathrm{f}\!:\!\mathrm{e}
& + & \mathrm{g}\!:\!\mathrm{f}
& + & \mathrm{h}\!:\!\mathrm{j}
& + & \mathrm{i}\!:\!\mathrm{h}
& + & \mathrm{j}\!:\!\mathrm{i}
\\[4pt]
\mathrm{h}
& = & \mathrm{e}\!:\!\mathrm{h}
& + & \mathrm{f}\!:\!\mathrm{j}
& + & \mathrm{g}\!:\!\mathrm{i}
& + & \mathrm{h}\!:\!\mathrm{e}
& + & \mathrm{i}\!:\!\mathrm{g}
& + & \mathrm{j}\!:\!\mathrm{f}
\\[4pt]
\mathrm{i}
& = & \mathrm{e}\!:\!\mathrm{i}
& + & \mathrm{f}\!:\!\mathrm{h}
& + & \mathrm{g}\!:\!\mathrm{j}
& + & \mathrm{h}\!:\!\mathrm{f}
& + & \mathrm{i}\!:\!\mathrm{e}
& + & \mathrm{j}\!:\!\mathrm{g}
\\[4pt]
\mathrm{j}
& = & \mathrm{e}\!:\!\mathrm{j}
& + & \mathrm{f}\!:\!\mathrm{i}
& + & \mathrm{g}\!:\!\mathrm{h}
& + & \mathrm{h}\!:\!\mathrm{g}
& + & \mathrm{i}\!:\!\mathrm{f}
& + & \mathrm{j}\!:\!\mathrm{e}
\end{array}\!\)
|
If the ante-rep looks different from the post-rep, it is just as it should be, as \(S_3~\!\) is non-abelian (non-commutative), and so the two representations differ in the details of their practical effects, though, of course, being representations of the same abstract group, they must be isomorphic.
|
|
the way of heaven and earth
is to be long continued
in their operation
without stopping
|
|
|
— i ching, hexagram 32
|
The Reader may be wondering what happened to the announced subject of Dynamics And Logic. What happened was a bit like this:
We made the observation that the shift operators \(\{ \mathrm{E}_{ij} \}\!\) form a transformation group that acts on the set of propositions of the form \(f : \mathbb{B} \times \mathbb{B} \to \mathbb{B}.\!\) Group theory is a very attractive subject, but it did not draw us so far from our intended course as one might initially think. For one thing, groups, especially the groups that are named after the Norwegian mathematician Marius Sophus Lie (1842–1899), have turned out to be of critical utility in the solution of differential equations. For another thing, group operations provide us with an ample supply of triadic relations that have been extremely well-studied over the years, and thus they give us no small measure of useful guidance in the study of sign relations, another brand of 3-adic relations that have significance for logical studies, and in our acquaintance with which we have barely begun to break the ice. Finally, I couldn't resist taking up the links between group representations, amounting to the very archetypes of logical models, and the pragmatic maxim.
We've seen a couple of groups, \(V_4\!\) and \(S_3,\!\) represented in various ways, and we've seen their representations presented in a variety of different manners. Let us look at one other stylistic variant for presenting a representation that is frequently seen, the so-called matrix representation of a group.
Recalling the manner of our acquaintance with the symmetric group \(S_3,\!\) we began with the bigraph (bipartite graph) picture of its natural representation as the set of all permutations or substitutions on the set \(X = \{ a, b, c \}.\!\)
\(\text{Permutation Substitutions in}~ \mathrm{Sym} \{ a, b, c \}\!\)
| \(\mathrm{e}\!\)
|
\(\mathrm{f}\!\)
|
\(\mathrm{g}\!\)
|
\(\mathrm{h}\!\)
|
\(\mathrm{i}~\!\)
|
\(\mathrm{j}\!\)
|
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
a & b & c
\end{matrix}\!\)
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
c & a & b
\end{matrix}\!\)
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
b & c & a
\end{matrix}\!\)
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
a & c & b
\end{matrix}\!\)
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
c & b & a
\end{matrix}\!\)
|
\(\begin{matrix}
a & b & c
\\[3pt]
\downarrow & \downarrow & \downarrow
\\[6pt]
b & a & c
\end{matrix}\!\)
|
These permutations were then converted to relative form as logical sums of elementary relatives:
|
\(\begin{matrix}
\mathrm{e}
& = & a\!:\!a
& + & b\!:\!b
& + & c\!:\!c
\\[4pt]
\mathrm{f}
& = & a\!:\!c
& + & b\!:\!a
& + & c\!:\!b
\\[4pt]
\mathrm{g}
& = & a\!:\!b
& + & b\!:\!c
& + & c\!:\!a
\\[4pt]
\mathrm{h}
& = & a\!:\!a
& + & b\!:\!c
& + & c\!:\!b
\\[4pt]
\mathrm{i}
& = & a\!:\!c
& + & b\!:\!b
& + & c\!:\!a
\\[4pt]
\mathrm{j}
& = & a\!:\!b
& + & b\!:\!a
& + & c\!:\!c
\end{matrix}\!\)
|
From the relational representation of \(\mathrm{Sym} \{ a, b, c \} \cong S_3,\!\) one easily derives a linear representation of the group by viewing each permutation as a linear transformation that maps the elements of a suitable vector space onto each other. Each of these linear transformations is in turn represented by a 2-dimensional array of coefficients in \(\mathbb{B},\!\) resulting in the following set of matrices for the group:
\(\text{Matrix Representations of Permutations in}~ \mathrm{Sym}(3)\!\)
| \(\mathrm{e}\!\)
|
\(\mathrm{f}\!\)
|
\(\mathrm{g}\!\)
|
\(\mathrm{h}\!\)
|
\(\mathrm{i}~\!\)
|
\(\mathrm{j}\!\)
|
|
\(\begin{matrix}
1 & 0 & 0
\\
0 & 1 & 0
\\
0 & 0 & 1
\end{matrix}~\!\)
|
\(\begin{matrix}
0 & 0 & 1
\\
1 & 0 & 0
\\
0 & 1 & 0
\end{matrix}~\!\)
|
\(\begin{matrix}
0 & 1 & 0
\\
0 & 0 & 1
\\
1 & 0 & 0
\end{matrix}\!\)
|
\(\begin{matrix}
1 & 0 & 0
\\
0 & 0 & 1
\\
0 & 1 & 0
\end{matrix}~\!\)
|
\(\begin{matrix}
0 & 0 & 1
\\
0 & 1 & 0
\\
1 & 0 & 0
\end{matrix}~\!\)
|
\(\begin{matrix}
0 & 1 & 0
\\
1 & 0 & 0
\\
0 & 0 & 1
\end{matrix}~\!\)
|
The key to the mysteries of these matrices is revealed by observing that their coefficient entries are arrayed and overlaid on a place-mat marked like so:
|
\(\begin{bmatrix}
a\!:\!a &
a\!:\!b &
a\!:\!c
\\
b\!:\!a &
b\!:\!b &
b\!:\!c
\\
c\!:\!a &
c\!:\!b &
c\!:\!c
\end{bmatrix}\!\)
|
Logical Cacti
- Theme One Program — Logical Cacti
- http://stderr.org/pipermail/inquiry/2005-February/thread.html#2348
- http://stderr.org/pipermail/inquiry/2005-February/002360.html
- http://stderr.org/pipermail/inquiry/2005-February/002361.html
Original Version
Up till now we've been working to hammer out a two-edged sword of syntax, honing the syntax of painted and rooted cacti and expressions (PARCAE), and turning it to use in taming the syntax of two-level formal languages.
But the purpose of a logical syntax is to support a logical semantics, which means, for starters, to bear interpretation as sentential signs that can denote objective propositions about some universe of objects.
One of the difficulties that we face in this discussion is that the words interpretation, meaning, semantics, and so on will have so many different meanings from one moment to the next of their use. A dedicated neologician might be able to think up distinctive names for all of the aspects of meaning and all of the approaches to them that will concern us here, but I will just have to do the best that I can with the common lot of ambiguous terms, leaving it to context and the intelligent interpreter to sort it out as much as possible.
As it happens, the language of cacti is so abstract that it can bear at least two different interpretations as logical sentences denoting logical propositions. The two interpretations that I know about are descended from the ones that Charles Sanders Peirce called the entitative and the existential interpretations of his systems of graphical logics. For our present aims, I shall briefly introduce the alternatives and then quickly move to the existential interpretation of logical cacti.
Table A illustrates the existential interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.
\(\text{Table A.}~~\text{Existential Interpretation}\)
| \(\text{Cactus Graph}\!\)
|
\(\text{Cactus Expression}\!\)
|
\(\text{Interpretation}\!\)
|
|
\({}^{\backprime\backprime}\texttt{~}{}^{\prime\prime}\)
|
\(\operatorname{true}.\)
|
|
\(\texttt{(~)}\)
|
\(\operatorname{false}.\)
|
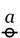
|
\(a\!\)
|
\(a.\!\)
|

|
\(\texttt{(} a \texttt{)}\)
|
\(\begin{matrix}
\tilde{a}
\\[2pt]
a^\prime
\\[2pt]
\lnot a
\\[2pt]
\operatorname{not}~ a.
\end{matrix}\)
|
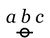
|
\(a~b~c\)
|
\(\begin{matrix}
a \land b \land c
\\[6pt]
a ~\operatorname{and}~ b ~\operatorname{and}~ c.
\end{matrix}\)
|
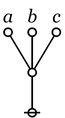
|
\(\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}\)
|
\(\begin{matrix}
a \lor b \lor c
\\[6pt]
a ~\operatorname{or}~ b ~\operatorname{or}~ c.
\end{matrix}\)
|
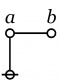
|
\(\texttt{(} a \texttt{(} b \texttt{))}\)
|
\(\begin{matrix}
a \Rightarrow b
\\[2pt]
a ~\operatorname{implies}~ b.
\\[2pt]
\operatorname{if}~ a ~\operatorname{then}~ b.
\\[2pt]
\operatorname{not}~ a ~\operatorname{without}~ b.
\end{matrix}\)
|
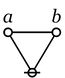
|
\(\texttt{(} a \texttt{,} b \texttt{)}\)
|
\(\begin{matrix}
a + b
\\[2pt]
a \neq b
\\[2pt]
a ~\operatorname{exclusive-or}~ b.
\\[2pt]
a ~\operatorname{not~equal~to}~ b.
\end{matrix}\)
|
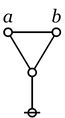
|
\(\texttt{((} a \texttt{,} b \texttt{))}\)
|
\(\begin{matrix}
a = b
\\[2pt]
a \iff b
\\[2pt]
a ~\operatorname{equals}~ b.
\\[2pt]
a ~\operatorname{if~and~only~if}~ b.
\end{matrix}\)
|
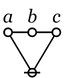
|
\(\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}\)
|
\(\begin{matrix}
\operatorname{just~one~of}
\\
a, b, c
\\
\operatorname{is~false}.
\end{matrix}\)
|
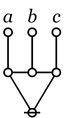
|
\(\texttt{((} a \texttt{),(} b \texttt{),(} c \texttt{))}\)
|
\(\begin{matrix}
\operatorname{just~one~of}
\\
a, b, c
\\
\operatorname{is~true}.
\end{matrix}\)
|
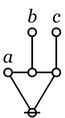
|
\(\texttt{(} a \texttt{,(} b \texttt{),(} c \texttt{))}\)
|
\(\begin{matrix}
\operatorname{genus}~ a ~\operatorname{of~species}~ b, c.
\\[6pt]
\operatorname{partition}~ a ~\operatorname{into}~ b, c.
\\[6pt]
\operatorname{pie}~ a ~\operatorname{of~slices}~ b, c.
\end{matrix}\)
|
Table B illustrates the entitative interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.
\(\text{Table B.}~~\text{Entitative Interpretation}\)
| \(\text{Cactus Graph}\!\)
|
\(\text{Cactus Expression}\!\)
|
\(\text{Interpretation}\!\)
|
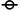
|
\({}^{\backprime\backprime}\texttt{~}{}^{\prime\prime}\)
|
\(\operatorname{false}.\)
|
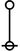
|
\(\texttt{(~)}\)
|
\(\operatorname{true}.\)
|
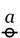
|
\(a\!\)
|
\(a.\!\)
|

|
\(\texttt{(} a \texttt{)}\)
|
\(\begin{matrix}
\tilde{a}
\\[2pt]
a^\prime
\\[2pt]
\lnot a
\\[2pt]
\operatorname{not}~ a.
\end{matrix}\)
|
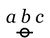
|
\(a~b~c\)
|
\(\begin{matrix}
a \lor b \lor c
\\[6pt]
a ~\operatorname{or}~ b ~\operatorname{or}~ c.
\end{matrix}\)
|

|
\(\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}\)
|
\(\begin{matrix}
a \land b \land c
\\[6pt]
a ~\operatorname{and}~ b ~\operatorname{and}~ c.
\end{matrix}\)
|
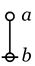
|
\(\texttt{(} a \texttt{)} b\)
|
\(\begin{matrix}
a \Rightarrow b
\\[2pt]
a ~\operatorname{implies}~ b.
\\[2pt]
\operatorname{if}~ a ~\operatorname{then}~ b.
\\[2pt]
\operatorname{not}~ a, ~\operatorname{or}~ b.
\end{matrix}\)
|

|
\(\texttt{(} a \texttt{,} b \texttt{)}\)
|
\(\begin{matrix}
a = b
\\[2pt]
a \iff b
\\[2pt]
a ~\operatorname{equals}~ b.
\\[2pt]
a ~\operatorname{if~and~only~if}~ b.
\end{matrix}\)
|

|
\(\texttt{((} a \texttt{,} b \texttt{))}\)
|
\(\begin{matrix}
a + b
\\[2pt]
a \neq b
\\[2pt]
a ~\operatorname{exclusive-or}~ b.
\\[2pt]
a ~\operatorname{not~equal~to}~ b.
\end{matrix}\)
|

|
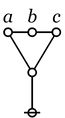
\(\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}\)
|
\(\begin{matrix}
\operatorname{not~just~one~of}
\\
a, b, c
\\
\operatorname{is~true}.
\end{matrix}\)
|
|
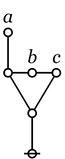
\(\texttt{((} a \texttt{,} b \texttt{,} c \texttt{))}\)
|
\(\begin{matrix}
\operatorname{just~one~of}
\\
a, b, c
\\
\operatorname{is~true}.
\end{matrix}\)
|
|
\(\texttt{(((} a \texttt{),} b \texttt{,} c \texttt{))}\)
|
\(\begin{matrix}
\operatorname{genus}~ a ~\operatorname{of~species}~ b, c.
\\[6pt]
\operatorname{partition}~ a ~\operatorname{into}~ b, c.
\\[6pt]
\operatorname{pie}~ a ~\operatorname{of~slices}~ b, c.
\end{matrix}\)
|
For the time being, the main things to take away from Tables A and B are the ideas that the compositional structure of cactus graphs and expressions can be articulated in terms of two different kinds of connective operations, and that there are two distinct ways of mapping this compositional structure into the compositional structure of propositional sentences, say, in English:
| 1.
|
The node connective joins a number of component cacti \(C_1, \ldots, C_k\) at a node:
|
|
|
C_1 ... C_k
@
|
| 2.
|
The lobe connective joins a number of component cacti \(C_1, \ldots, C_k\) to a lobe:
|
|
|
C_1 C_2 C_k
o---o-...-o
\ /
\ /
\ /
\ /
@
|
Table 15 summarizes the existential and entitative interpretations of the primitive cactus structures, in effect, the graphical constants and connectives.
Table 15. Existential & Entitative Interpretations of Cactus Structures
o-----------------o-----------------o-----------------o-----------------o
| Cactus Graph | Cactus String | Existential | Entitative |
| | | Interpretation | Interpretation |
o-----------------o-----------------o-----------------o-----------------o
| | | | |
| @ | " " | true | false |
| | | | |
o-----------------o-----------------o-----------------o-----------------o
| | | | |
| o | | | |
| | | | | |
| @ | ( ) | false | true |
| | | | |
o-----------------o-----------------o-----------------o-----------------o
| | | | |
| C_1 ... C_k | | | |
| @ | C_1 ... C_k | C_1 & ... & C_k | C_1 v ... v C_k |
| | | | |
o-----------------o-----------------o-----------------o-----------------o
| | | | |
| C_1 C_2 C_k | | Just one | Not just one |
| o---o-...-o | | | |
| \ / | | of the C_j, | of the C_j, |
| \ / | | | |
| \ / | | j = 1 to k, | j = 1 to k, |
| \ / | | | |
| @ | (C_1, ..., C_k) | is not true. | is true. |
| | | | |
o-----------------o-----------------o-----------------o-----------------o
|
It is possible to specify abstract rules of equivalence (AROEs) between cacti, rules for transforming one cactus into another that are formal in the sense of being indifferent to the above choices for logical or semantic interpretations, and that partition the set of cacti into formal equivalence classes.
A reduction is an equivalence transformation that is applied in the direction of decreasing graphical complexity.
A basic reduction is a reduction that applies to one of the two families of basic connectives.
Table 16 schematizes the two types of basic reductions in a purely formal, interpretation-independent fashion.
Table 16. Basic Reductions
o---------------------------------------o
| |
| C_1 ... C_k |
| @ = @ |
| |
| if and only if |
| |
| C_j = @ for all j = 1 to k |
| |
o---------------------------------------o
| |
| C_1 C_2 C_k |
| o---o-...-o |
| \ / |
| \ / |
| \ / |
| \ / |
| @ = @ |
| |
| if and only if |
| |
| o |
| | |
| C_j = @ for exactly one j in [1, k] |
| |
o---------------------------------------o
|
The careful reader will have noticed that we have begun to use graphical paints like "a", "b", "c" and schematic proxies like "C_1", "C_j", "C_k" in a variety of novel and unjustified ways.
The careful writer would have already introduced a whole bevy of technical concepts and proved a whole crew of formal theorems to justify their use before contemplating this stage of development, but I have been hurrying to proceed with the informal exposition, and this expedition must leave steps to the reader's imagination.
Of course I mean the active imagination. So let me assist the prospective exercise with a few hints of what it would take to guarantee that these practices make sense.
Partial Rewrites
Table 13 illustrates the existential interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.
Even though I do most of my thinking in the existential interpretation, I will continue to speak of these forms as logical graphs, because I think it is an important fact about them that the formal validity of the axioms and theorems is not dependent on the choice between the entitative and the existential interpretations.
The first extension is the reflective extension of logical graphs (RefLog). It is obtained by generalizing the negation operator "\(\texttt{(~)}\)" in a certain way, calling "\(\texttt{(~)}\)" the controlled, moderated, or reflective negation operator of order 1, then adding another such operator for each finite \(k = 2, 3, \ldots .\)
In sum, these operators are symbolized by bracketed argument lists as follows: "\(\texttt{(~)}\)", "\(\texttt{(~,~)}\)", "\(\texttt{(~,~,~)}\)", …, where the number of slots is the order of the reflective negation operator in question.
The cactus graph and the cactus expression shown here are both described as a spike.
o---------------------------------------o
| |
| o |
| | |
| @ |
| |
o---------------------------------------o
| ( ) |
o---------------------------------------o
|
The rule of reduction for a lobe is:
o---------------------------------------o
| |
| x_1 x_2 ... x_k |
| o-----o--- ... ---o |
| \ / |
| \ / |
| \ / |
| \ / |
| \ / |
| \ / |
| \ / |
| \ / |
| @ = @ |
| |
o---------------------------------------o
|
if and only if exactly one of the \(x_j\!\) is a spike.
In Ref Log, an expression of the form \(\texttt{((}~ e_1 ~\texttt{),(}~ e_2 ~\texttt{),(}~ \ldots ~\texttt{),(}~ e_k ~\texttt{))}\)
expresses the fact that exactly one of the \(e_j\!\) is true. Expressions of this form are called universal partition expressions, and
they parse into a type of graph called a painted and rooted cactus (PARC):
o---------------------------------------o
| |
| e_1 e_2 ... e_k |
| o o o |
| | | | |
| o-----o--- ... ---o |
| \ / |
| \ / |
| \ / |
| \ / |
| \ / |
| \ / |
| \ / |
| \ / |
| @ |
| |
o---------------------------------------o
|
o---------------------------------------o
| |
| ( x1, x2, ..., xk ) = [blank] |
| |
| iff |
| |
| Just one of the arguments |
| x1, x2, ..., xk = () |
| |
o---------------------------------------o
|
The interpretation of these operators, read as assertions about the values of their listed arguments, is as follows:
| Existential Interpretation:
|
Just one of the k argument is false.
|
| Entitative Interpretation:
|
Not just one of the k arguments is true.
|
Tables
\(\text{Table 1.}~~\text{Syntax and Semantics of a Calculus for Propositional Logic}\)
| \(\text{Graph}\!\)
|
\(\text{Expression}\!\)
|
\(\text{Interpretation}\!\)
|
\(\text{Other Notations}\!\)
|
|
\(~\)
|
\(\operatorname{true}\)
|
\(1\!\)
|
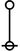
|
\(\texttt{(~)}\)
|
\(\operatorname{false}\)
|
\(0\!\)
|
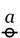
|
\(a\!\)
|
\(a\!\)
|
\(a\!\)
|

|
\(\texttt{(} a \texttt{)}\)
|
\(\operatorname{not}~ a\)
|
\(\lnot a \quad \bar{a} \quad \tilde{a} \quad a^\prime\)
|
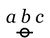
|
\(a ~ b ~ c\)
|
\(a ~\operatorname{and}~ b ~\operatorname{and}~ c\)
|
\(a \land b \land c\)
|

|
\(\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}\)
|
\(a ~\operatorname{or}~ b ~\operatorname{or}~ c\)
|
\(a \lor b \lor c\)
|

|
\(\texttt{(} a \texttt{(} b \texttt{))}\)
|
\(\begin{matrix}
a ~\operatorname{implies}~ b
\\[6pt]
\operatorname{if}~ a ~\operatorname{then}~ b
\end{matrix}\)
|
\(a \Rightarrow b\)
|

|
\(\texttt{(} a \texttt{,} b \texttt{)}\)
|
\(\begin{matrix}
a ~\operatorname{not~equal~to}~ b
\\[6pt]
a ~\operatorname{exclusive~or}~ b
\end{matrix}\)
|
\(\begin{matrix}
a \neq b
\\[6pt]
a + b
\end{matrix}\)
|

|
\(\texttt{((} a \texttt{,} b \texttt{))}\)
|
\(\begin{matrix}
a ~\operatorname{is~equal~to}~ b
\\[6pt]
a ~\operatorname{if~and~only~if}~ b
\end{matrix}\)
|
\(\begin{matrix}
a = b
\\[6pt]
a \Leftrightarrow b
\end{matrix}\)
|

|
\(\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}\)
|
\(\begin{matrix}
\operatorname{just~one~of}
\\
a, b, c
\\
\operatorname{is~false}.
\end{matrix}\)
|
\(\begin{matrix}
& \bar{a} ~ b ~ c
\\
\lor & a ~ \bar{b} ~ c
\\
\lor & a ~ b ~ \bar{c}
\end{matrix}\)
|

|
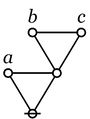
\(\texttt{((} a \texttt{),(} b \texttt{),(} c \texttt{))}\)
|
\(\begin{matrix}
\operatorname{just~one~of}
\\
a, b, c
\\
\operatorname{is~true}.
\\[6pt]
\operatorname{partition~all}
\\
\operatorname{into}~ a, b, c.
\end{matrix}\)
|
\(\begin{matrix}
& a ~ \bar{b} ~ \bar{c}
\\
\lor & \bar{a} ~ b ~ \bar{c}
\\
\lor & \bar{a} ~ \bar{b} ~ c
\end{matrix}\)
|
|
\(\texttt{(} a \texttt{,(} b \texttt{,} c \texttt{))}\)
|
\(\begin{matrix}
\operatorname{oddly~many~of}
\\
a, b, c
\\
\operatorname{are~true}.
\end{matrix}\)
|
\(a + b + c\!\)
\(\begin{matrix}
& a ~ b ~ c
\\
\lor & a ~ \bar{b} ~ \bar{c}
\\
\lor & \bar{a} ~ b ~ \bar{c}
\\
\lor & \bar{a} ~ \bar{b} ~ c
\end{matrix}\)
|
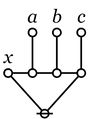
|
\(\texttt{(} x \texttt{,(} a \texttt{),(} b \texttt{),(} c \texttt{))}\)
|
\(\begin{matrix}
\operatorname{partition}~ x
\\
\operatorname{into}~ a, b, c.
\\[6pt]
\operatorname{genus}~ x ~\operatorname{comprises}
\\
\operatorname{species}~ a, b, c.
\end{matrix}\)
|
\(\begin{matrix}
& \bar{x} ~ \bar{a} ~ \bar{b} ~ \bar{c}
\\
\lor & x ~ a ~ \bar{b} ~ \bar{c}
\\
\lor & x ~ \bar{a} ~ b ~ \bar{c}
\\
\lor & x ~ \bar{a} ~ \bar{b} ~ c
\end{matrix}\)
|
\(\text{Table C.}~~\text{Dualing Interpretations}\)
| \(\text{Graph}\!\)
|
\(\text{String}\!\)
|
\(\text{Existential}\!\)
|
\(\text{Entitative}\!\)
|
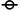
|
\({}^{\backprime\backprime}\texttt{~}{}^{\prime\prime}\)
|
\(\operatorname{true}.\)
|
\(\operatorname{false}.\)
|
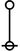
|
\(\texttt{(~)}\)
|
\(\operatorname{false}.\)
|
\(\operatorname{true}.\)
|
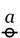
|
\(a\!\)
|
\(a.\!\)
|
\(a.\!\)
|

|
\(\texttt{(} a \texttt{)}\)
|
\(\lnot a\)
|
\(\lnot a\)
|
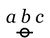
|
\(a~b~c\)
|
\(a \land b \land c\)
|
\(a \lor b \lor c\)
|

|
\(\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}\)
|
\(a \lor b \lor c\)
|
\(a \land b \land c\)
|

|
\(\texttt{(} a \texttt{(} b \texttt{))}\)
|
\(a \Rightarrow b\)
|
|
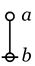
|
\(\texttt{(} a \texttt{)} b\)
|
|
\(a \Rightarrow b\)
|

|
\(\texttt{(} a \texttt{,} b \texttt{)}\)
|
\(a \neq b\)
|
\(a = b\!\)
|

|
\(\texttt{((} a \texttt{,} b \texttt{))}\)
|
\(a = b\!\)
|
\(a \neq b\!\)
|

|
\(\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}\)
|
\(\begin{matrix}
\operatorname{just~one}
\\
\operatorname{of}~ a, b, c
\\
\operatorname{is~false}.
\end{matrix}\)
|
\(\begin{matrix}
\operatorname{not~just~one}
\\
\operatorname{of}~ a, b, c
\\
\operatorname{is~true}.
\end{matrix}\)
|

|
\(\texttt{((} a \texttt{),(} b \texttt{),(} c \texttt{))}\)
|
\(\begin{matrix}
\operatorname{just~one}
\\
\operatorname{of}~ a, b, c
\\
\operatorname{is~true}.
\end{matrix}\)
|
\(\begin{matrix}
\operatorname{not~just~one}
\\
\operatorname{of}~ a, b, c
\\
\operatorname{is~false}.
\end{matrix}\)
|

|
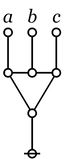
\(\texttt{((} a \texttt{,} b \texttt{,} c \texttt{))}\)
|
\(\begin{matrix}
\operatorname{not~just~one}
\\
\operatorname{of}~ a, b, c
\\
\operatorname{is~false}.
\end{matrix}\)
|
\(\begin{matrix}
\operatorname{just~one}
\\
\operatorname{of}~ a, b, c
\\
\operatorname{is~true}.
\end{matrix}\)
|
|
\(\texttt{(((} a \texttt{),(} b \texttt{),(} c \texttt{)))}\)
|
\(\begin{matrix}
\operatorname{not~just~one}
\\
\operatorname{of}~ a, b, c
\\
\operatorname{is~true}.
\end{matrix}\)
|
\(\begin{matrix}
\operatorname{just~one}
\\
\operatorname{of}~ a, b, c
\\
\operatorname{is~false}.
\end{matrix}\)
|

|
\(\texttt{(} a \texttt{,(} b \texttt{),(} c \texttt{))}\)
|
\(\begin{matrix}
\operatorname{partition}~ a
\\
\operatorname{into}~ b, c.
\end{matrix}\)
|
|

|
\(\texttt{(((} a \texttt{),} b \texttt{,} c \texttt{))}\)
|
|
\(\begin{matrix}
\operatorname{partition}~ a
\\
\operatorname{into}~ b, c.
\end{matrix}\)
|
|












