|
\(\begin{matrix}
(~) & = & 0 & = & \operatorname{false}
\'"`UNIQ-MathJax1-QINU`"'
* The point \((0, 0, \ldots , 0, 0)\) with all 0's as coordinates is the point where the conjunction of all negated variables evaluates to \(1,\!\) namely, the point where:
- \[(x_1)(x_2)\ldots(x_{n-1})(x_n) = 1.\]
To pass from these limiting examples to the general case, observe that a singular proposition \(s : \mathbb{B}^k \to \mathbb{B}\) can be given canonical expression as a conjunction of literals, \(s = e_1 e_2 \ldots e_{k-1} e_k\). Then the proposition \(\nu (e_1, e_2, \ldots, e_{k-1}, e_k)\) is \(1\!\) on the points adjacent to the point where \(s\!\) is \(1,\!\) and 0 everywhere else on the cube.
For example, consider the case where \(k = 3.\!\) Then the minimal negation operation \(\nu (p, q, r)\!\), when there is no risk of confusion written more simply as \((p, q, r)\!\), has the following venn diagram:
|
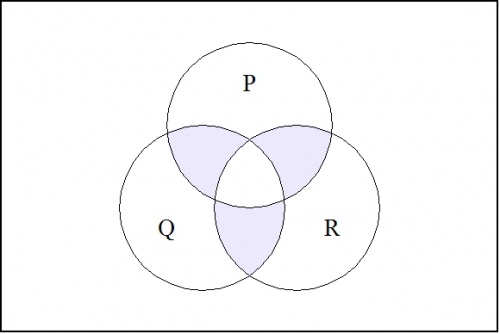
\(\text{Figure 1.}\quad (p, q, r)\!\)
|
For a contrasting example, the boolean function expressed by the form \(((p),(q),(r))\!\) has the following venn diagram:
|
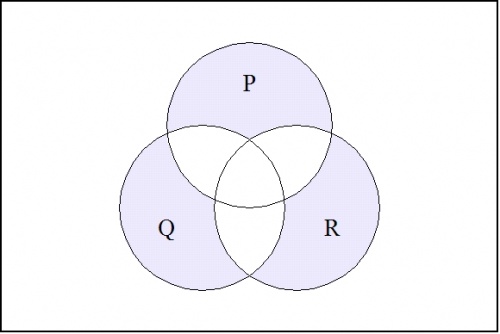
\(\text{Figure 2.}\quad ((p),(q),(r))\!\)
|
Glossary of basic terms
- Boolean domain
- A boolean domain \(\mathbb{B}\) is a generic 2-element set, for example, \(\mathbb{B} = \{ 0, 1 \},\) whose elements are interpreted as logical values, usually but not invariably with \(0 = \operatorname{false}\) and \(1 = \operatorname{true}.\)
- Boolean variable
- A boolean variable \(x\!\) is a variable that takes its value from a boolean domain, as \(x \in \mathbb{B}.\)
- Proposition
- In situations where boolean values are interpreted as logical values, a boolean-valued function \(f : X \to \mathbb{B}\) or a boolean function \(g : \mathbb{B}^k \to \mathbb{B}\) is frequently called a proposition.
- Basis element, Coordinate projection
- Given a sequence of \(k\!\) boolean variables, \(x_1, \ldots, x_k,\) each variable \(x_j\!\) may be treated either as a basis element of the space \(\mathbb{B}^k\) or as a coordinate projection \(x_j : \mathbb{B}^k \to \mathbb{B}.\)
- Basic proposition
- This means that the set of objects \(\{ x_j : 1 \le j \le k \}\) is a set of boolean functions \(\{ x_j : \mathbb{B}^k \to \mathbb{B} \}\) subject to logical interpretation as a set of basic propositions that collectively generate the complete set of \(2^{2^k}\) propositions over \(\mathbb{B}^k.\)
- A literal is one of the 2k propositions x1, …, xk, (x1), …, (xk), in other words, either a posited basic proposition xj or a negated basic proposition (xj), for some j = 1 to k.
- In mathematics generally, the fiber of a point y under a function f : X → Y is defined as the inverse image \(f^{-1}(y)\).
- In the case of a boolean function f : Bk → B, there are just two fibers:
- The fiber of 0 under f, defined as \(f^{-1}(0)\), is the set of points where f is 0.
- The fiber of 1 under f, defined as \(f^{-1}(1)\), is the set of points where f is 1.
- When 1 is interpreted as the logical value true, then \(f^{-1}(1)\) is called the fiber of truth in the proposition f. Frequent mention of this fiber makes it useful to have a shorter way of referring to it. This leads to the definition of the notation \([|f|] = f^{-1}(1)\!\) for the fiber of truth in the proposition f.
- A singular boolean function s : Bk → B is a boolean function whose fiber of 1 is a single point of Bk.
- In the interpretation where 1 equals true, a singular boolean function is called a singular proposition.
- Singular boolean functions and singular propositions serve as functional or logical representatives of the points in Bk.
- A singular conjunction in Bk → B is a conjunction of k literals that includes just one conjunct of the pair \(\{ x_j,\ \nu (x_j) \}\) for each j = 1 to k.
- A singular proposition s : Bk → B can be expressed as a singular conjunction:
| \(s ~=~ e_1 e_2 \ldots e_{k-1} e_k\),
|
|
\(\begin{array}{llll}
\text{where} & e_j & = & x_j
\\[6pt]
\text{or} & e_j & = & \nu (x_j),
\\[6pt]
\text{for} & j & = & 1 ~\text{to}~ k.
\end{array}\)
|
See also
Template:Col-breakTemplate:Col-breakTemplate:Col-breakTemplate:Col-endExternal linksAficionados
<sharethis />
|

